一种基于调制m序列的直接序列扩频信号调制方法

曾凌川; 白燕; 卢晓春; 袁洪; 宿晨庚; 吴小婧

doi:10.11999/JEIT200600

一种基于调制m序列的直接序列扩频信号调制方法

doi: 10.11999/JEIT200600

曾凌川^{1, 2, 3},
白燕^2, ,,
卢晓春²,
袁洪³,
宿晨庚⁴,
吴小婧³

1.
中国科学院大学电子电气与通信工程学院北京 101408
2.
中国科学院国家授时中心西安 710600
3.
中国科学院空天信息创新研究院北京 100094
4.
北京跟踪与通信技术研究所北京 100094

基金项目: 国家自然科学基金(11873009)

详细信息

作者简介:
曾凌川：男，1988年生，博士生，研究方向为导航卫星星间链路技术

白燕：女，1975年生，研究员，研究方向为导航卫星星间链路技术

卢晓春：女，1970年生，研究员，研究方向为卫星导航与时间同步技术

袁洪：男，1968年生，研究员，研究方向为电离层物理及电离层探测技术

宿晨庚：男，1988年生，助理研究员，研究方向为卫星导航信号设计与试验验证

吴小婧：女，1987年生，工程师，研究方向为导航卫星星间链路技术

通讯作者:
白燕　by@ntsc.ac.cn

中图分类号: TN925.91
计量
- 文章访问数: 1667
- HTML全文浏览量: 1029
- PDF下载量: 156
- 被引次数: 0
出版历程
- 收稿日期: 2020-07-21
- 修回日期: 2021-02-04
- 网络出版日期: 2021-03-01
- 刊出日期: 2021-08-10

A Signal Modulation Method of Direct Sequence Spread Spectrum Based on Modulated m-sequence

Lingchuan ZENG^{1, 2, 3},
Yan BAI^{2
, ,},
Xiaochun LU²,
Hong YUAN³,
Chengeng SU⁴,
Xiaojing WU³

1.
School of Electronic,Electrical and Communication Engineering, University of Chinese Academy of Sciences, Beijing 101408, China
2.
Nation Time Service Center, Chinese Academy of Sciences, Xi’an 710600, China
3.
Aerospace Information Research Institute, Chinese Academy of Sciences, Beijing 100094, China
4.
Beijing Institute of Tracking and Telecommunications Technology, Beijing 100094, China

Funds: General Fund of National Natural Science of China (11873009)

摘要

摘要: 为提高直接序列扩频通信系统的频谱利用率，该文提出在m序列周期等于信息比特位宽整数倍情况下的直接序列扩频信号——调制m序列的信号调制与解调方法(m-DSSS)。首先结合调制m序列相关性数值仿真结果验证m-DSSS信号捕获可行性，然后根据信息比特的排列组合情况，设计一种基于多通道的m-DSSS信号调制和解调方法，并对m-DSSS信号通过加性高斯白噪声信道后的抗干扰能力建立数学模型。最后在相同频谱利用率条件下，与码移键控(CSK)调制方式进行了仿真对比试验。仿真结果表明，m-DSSS信号不仅比CSK信号具有更低的副峰，且当载波采用BPSK调制时，m-DSSS还可通过判断极性来辅助信号捕获，在误码率优于1e-3条件下，m-DSSS信号比CSK信号有2 dB以上优势，验证了m-DSSS调制用于直扩系统的可行性。
- 直接序列扩频 /
- 伪随机序列 /
- 调制m序列 /
- 信号调制
Abstract: To raise the spectrum utilization, a modulation and demodulation method called modulated Direct Sequence Spread Spectrum (m-DSSS) is proposed, which assign the period of m-sequence to be equal to the integer multiple of data bit. Firstly, the feasibility of m-DSSS signal acquisition is verified by numerical simulation results of correlation. Then, according to the permutation of information bits, a multi-channel signal modulation and demodulation method for m-DSSS is designed, and the mathematical model reacting the anti-interference ability of passing through the additive Gaussian white noise channel is established. Finally, the simulation and contrast test are carried out with Codes Shift Keying (CSK) modulation under the same spectrum utilization. The simulation results show that m-DSSS signal not only has lower side peak than CSK signal but also can assist signal acquisition by judging polarity when BPSK modulation is adopted. When bit error rate is better than 1e-3, m-DSSS signal has more than 2 dB advantage than CSK signal, which verifies the feasibility of m-DSSS used in DSSS system.
- Direct Sequence Spread Spectrum (DSSS) /
- Pseudo-random sequence /
- Modulated m-sequence /
- Signal modulation

HTML全文

图 1 调制伪随机序列示意图

下载: 全尺寸图片幻灯片

图 2 基于10级调制m序列的信号调制原理示意图

下载: 全尺寸图片幻灯片

图 3 m序列$A$与其生成调制m序列相关性仿真

下载: 全尺寸图片幻灯片

图 4 m序列$A$与m序列$B$生成调制m序列相关性仿真

下载: 全尺寸图片幻灯片

图 5 CSK调制接收端相关运算示意图

下载: 全尺寸图片幻灯片

图 6 基于10级调制m序列的信号解调原理示意图

下载: 全尺寸图片幻灯片

图 7 8通道条件下m-DSSS各支路接收相关性仿真结果

下载: 全尺寸图片幻灯片

图 8 8通道条件下CSK调制各支路接收相关性仿真结果

下载: 全尺寸图片幻灯片

图 9 误码率仿真结果

下载: 全尺寸图片幻灯片

表 1 10级调制m序列与信息比特对应关系

信息比特组合	第1组码片与原 m序列对应码片的相位关系	第2组码片与原 m序列对应码片的相位关系	第3组码片与原 m序列对应码片的相位关系
000	反相	反相	反相
001	反相	反相	同相
010	反相	同相	反相
011	反相	同相	同相
100	同相	反相	反相
101	同相	反相	同相
110	同相	同相	反相
111	同相	同相	同相

下载: 导出CSV

表 2 8通道条件下信号捕获仿真试验参数

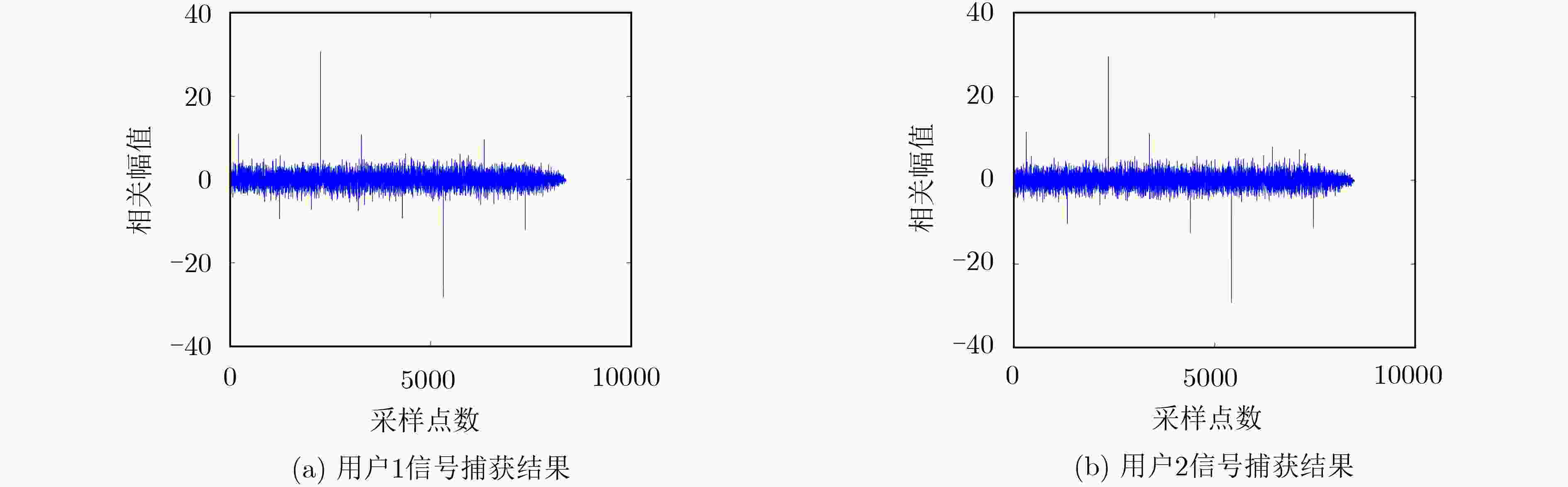
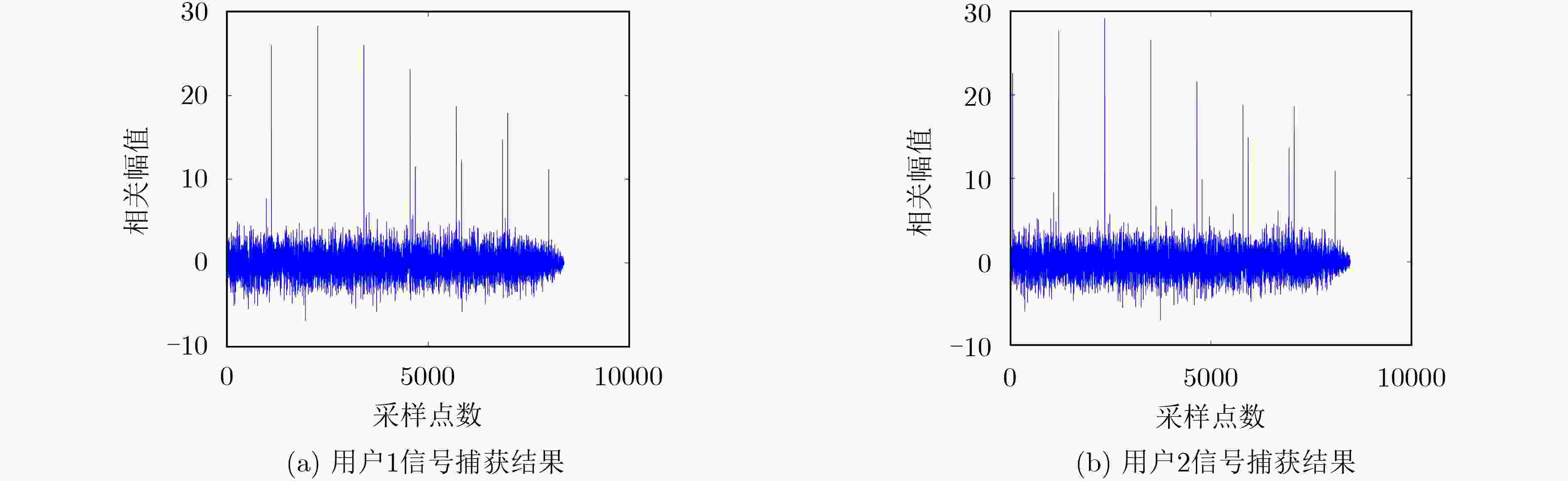
参数类型	用户1	用户2
m序列生成多项式	x¹⁰+x³+1	x¹⁰+x⁴+x³+x¹+1
m-DSSS每个周期调制比特数	3	3
CSK循环移位次数	8	8
CSK每次循环移位码片数	128(7次)、127(1次)	128(7次)、127(1次)
载波调制方式	BPSK	BPSK
载波频率(Hz)	2500	2500
信号采样频率(Hz)	100000	100000
信号延迟(扩频码片数)	200	300
信噪比(dB)	–15	–15
信号数据长度(扩频码片数)	8184	8184
相关运算步进长度(扩频码片数)	1	1

下载: 导出CSV

参考文献(19)

[1]	谢刚. GPS原理与接收机设计[M]. 北京: 电子工业出版社, 2011: 304–344. XIE Gang. Principles of GPS and Receiver Design[M]. Beijing: Publishing House of Electronics Industry, 2011: 304–344.
[2]	贺成艳, 郭际, 卢晓春, 等. 北斗卫星导航系统B1信号伪距偏差问题研究[J]. 电子与信息学报, 2018, 40(11): 2698–2704. doi: 10.11999/JEIT180074 HE Chengyan, GUO Ji, LU Xiaochun, et al. Researches on pseudo-range biases of BeiDou navigation satellite system B1 signals[J]. Journal of Electronics &Information Technology, 2018, 40(11): 2698–2704. doi: 10.11999/JEIT180074
[3]	RUAN Rengui, JIA Xiaolin, FENG Laiping, et al. Orbit determination and time synchronization for BDS-3 satellites with raw inter-satellite link ranging observations[J]. Satellite Navigation, 2020, 1(1): 8. doi: 10.1186/s43020-020-0008-y
[4]	何典. 测控数传一体化信道关键技术研究[D]. [硕士论文], 电子科技大学, 2019. HE Dian. Research on key technologies of TT&C data transmission integrated channel[D]. [Master dissertation], University of Electronic Science and Technology of China, 2019.
[5]	夏高峰, 罗宇, 金哲仕. 多进制直接序列扩频系统性能分析及仿真[J]. 航空电子技术, 2015, 46(2): 12–15, 20. doi: 10.3969/j.issn.1006-141X.2015.02.06 XIA Gaofeng, LUO Yu, and JIN Zheshi. Performance analysis and simulation of M-ary direct sequence spread spectrum system[J]. Avionics Technology, 2015, 46(2): 12–15, 20. doi: 10.3969/j.issn.1006-141X.2015.02.06
[6]	靳舒馨, 姚铮, 贾深惠, 等. 高速率GNSS电文多进制编码调制技术[J]. 北京邮电大学学报, 2018, 41(4): 97–103. doi: 10.13190/j.jbupt.2018-009 JIN Shuxin, YAO Zheng, JIA Shenhui, et al. High-speed non-binary coding and modulation techniques of GNSS message[J]. Journal of Beijing University of Posts and Telecommunications, 2018, 41(4): 97–103. doi: 10.13190/j.jbupt.2018-009
[7]	Cabinet Office. Quasi-zenith satellite system interface specification centimeter level augmentation service[R]. IS-QZSS-L6-001, 2018.
[8]	PEÑA A J G, SALÓS D, JULIEN O, et al. Analysis of the use of CSK for future GNSS signals[C]. The 26th International Technical Meeting of The Satellite Division of the Institute of Navigation, Nashville, USA, 2013: 1461–1479.
[9]	ANDREOTTI R, EMMANUELE A, FONTANELLA D, et al. Code-Shift-Keying (CSK) with advanced FEC coding for GNSS applications in satellite multipath channel[C]. The 7th ESA Workshop on Satellite Navigation Technologies and European Workshop on GNSS Signals and Signal Processing, Noordwijk, Netherlands, 2014: 1–8.
[10]	CHAUVAT R, PENA A G, ANGHILERI M, et al. Ultra-sparse binary LDPC codes with CSK signals for increased data rates in future GNSS[C]. The 9th ESA Workshop on Satellite Navigation Technologies and European Workshop on GNSS Signals and Signal Processing, Noordwijk, Netherlands, 2018: 1–11.
[11]	UNDERBERG L, WULF A, CROONENBROECK R, et al. Parallel sequence spread spectrum: Analytical and simulative approach for determination of bit error probability[C]. The 21st IEEE International Conference on Emerging Technologies and Factory Automation, Berlin, Germany, 2016: 1–8.
[12]	JIANG Xiaofei, GUO Lili, WANG Bailing, et al. Performance analysis for UWB system based on parallel combinatory spread spectrum using different pseudo-noise sequences[C]. The 2nd International Conference on Education Technology and Computer, Shanghai, China, 2010: 213–216.
[13]	刘佳鑫. 并行组合扩频系统伪码同步相关技术研究[D]. [硕士论文], 哈尔滨工程大学, 2014. LIU Jiaxin. Research on pseudo-random codes synchronization for PCSS systems[D]. [Master dissertation], Harbin Engineering University, 2014.
[14]	KADDOUM G, AHMED M F A, and NIJSURE Y. Code index modulation: A high data rate and energy efficient communication system[J]. IEEE Communications Letters, 2015, 19(2): 175–178. doi: 10.1109/LCOMM.2014.2385054
[15]	KADDOUM G and SOUJERI E. On the comparison between code-index modulation and spatial modulation techniques[C]. 2015 International Conference on Information and Communication Technology Research, Abu Dhabi, United Arab Emirates, 2015: 24–27.
[16]	葛利嘉, 江治林, 冯胜, 等. 非正交-码索引调制方法[J]. 电子与信息学报, 2018, 40(10): 2331–2336. doi: 10.11999/JEIT180023 GE Lijia, JIANG Zhilin, FENG Sheng, et al. Non-orthogonal-code index modulation[J]. Journal of Electronics &Information Technology, 2018, 40(10): 2331–2336. doi: 10.11999/JEIT180023
[17]	江治林. 基于直接序列扩频的码索引调制方案研究[D]. [硕士论文]. 重庆邮电大学, 2018. JIANG Zhilin. Research on code index modulation scheme based on direct sequence spread spectrum[D]. [Master dissertation], Chongqing University of Posts and Telecommunications, 2018.
[18]	贺利芳, 陈俊, 张天骐. 短参考多用户差分混沌移位键控通信系统性能分析[J]. 电子与信息学报, 2020, 42(8): 1902–1909. doi: 10.11999/JEIT190117 HE Lifang, CHEN Jun, and ZHANG Tianqi. Performance analysis of short reference multi-user differential chaos shift keying communication system[J]. Journal of Electronics &Information Technology, 2020, 42(8): 1902–1909. doi: 10.11999/JEIT190117
[19]	万哲先. 代数和编码[M]. 北京: 高等教育出版社, 2007: 239–250. WAN Zhexian. Algebra and Coding[M]. Beijing: Higher Education Press, 2007: 239–250.