基于密集特征融合的无监督单目深度估计

陈莹; 王一良

doi:10.11999/JEIT200590

基于密集特征融合的无监督单目深度估计

doi: 10.11999/JEIT200590

陈莹^,,
王一良

江南大学轻工过程先进控制教育部重点实验室无锡 214122

基金项目: 国家自然科学基金(61573168)

详细信息

作者简介:
陈莹：女，1976年生，教授，博士，研究方向为信息融合、模式识别

王一良：男，1997年生，硕士生，研究方向为计算机视觉与模式识别

通讯作者:
陈莹　chenying@jiangnan.edu.cn

中图分类号: TN911.73; TP391
计量
- 文章访问数: 1336
- HTML全文浏览量: 391
- PDF下载量: 118
- 被引次数: 0
出版历程
- 收稿日期: 2020-07-17
- 修回日期: 2020-12-29
- 网络出版日期: 2021-02-03
- 刊出日期: 2021-10-18

Unsupervised Monocular Depth Estimation Based on Dense Feature Fusion

Ying CHEN^,,
Yiliang WANG

Key Laboratory of Advanced Process Control for Light Industry (Ministry of Education), Jiangnan University, Wuxi 214122, China

Funds: The National Natural Science Foundation of China (61573168)

摘要

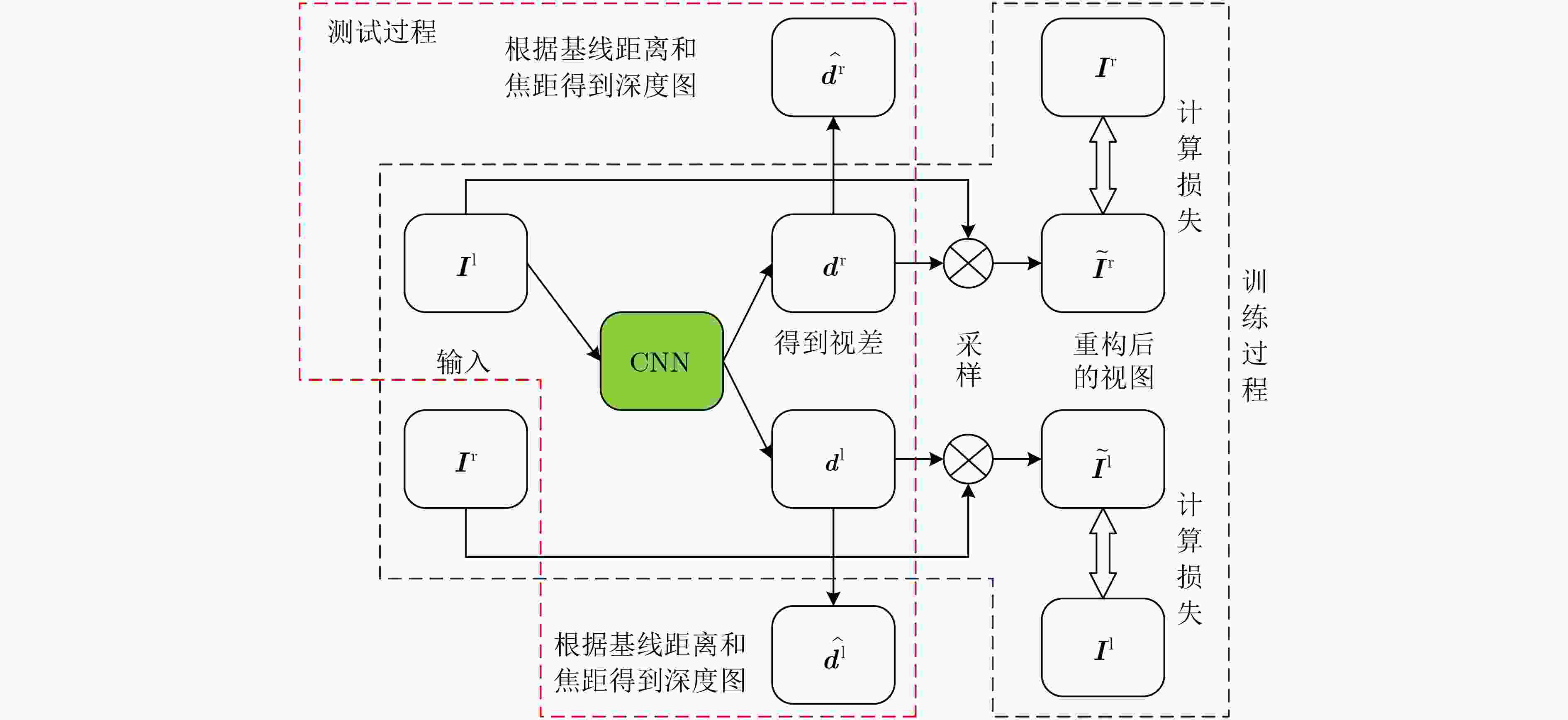
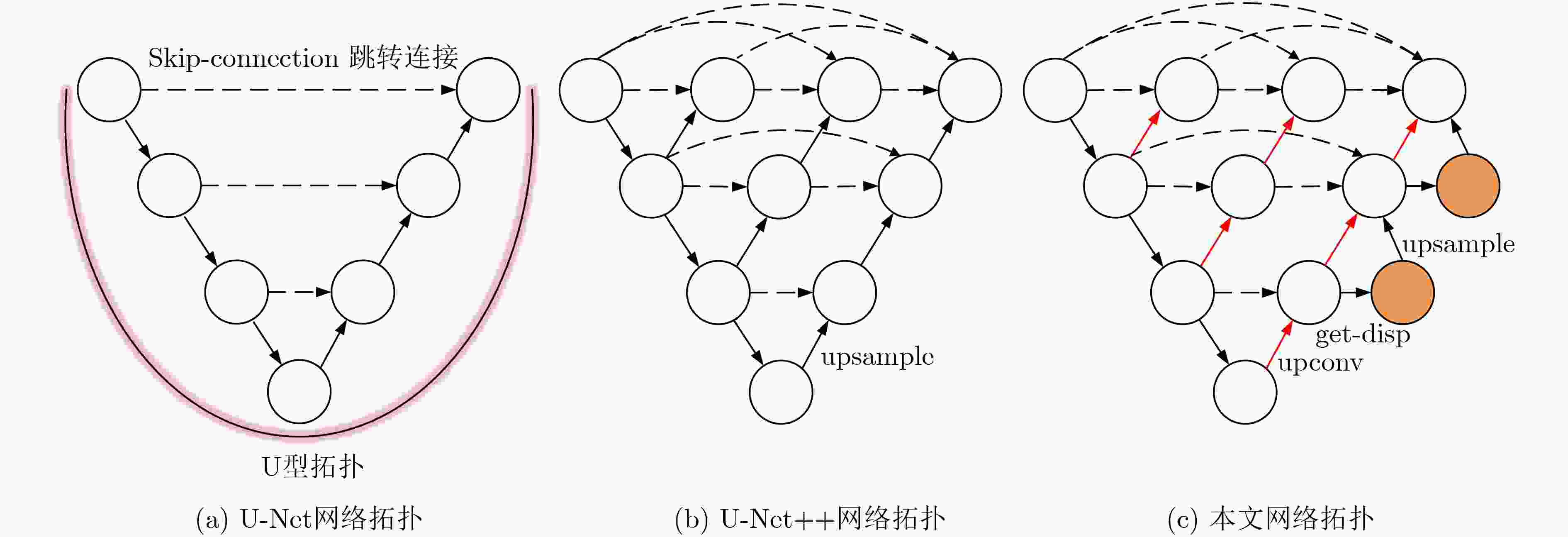
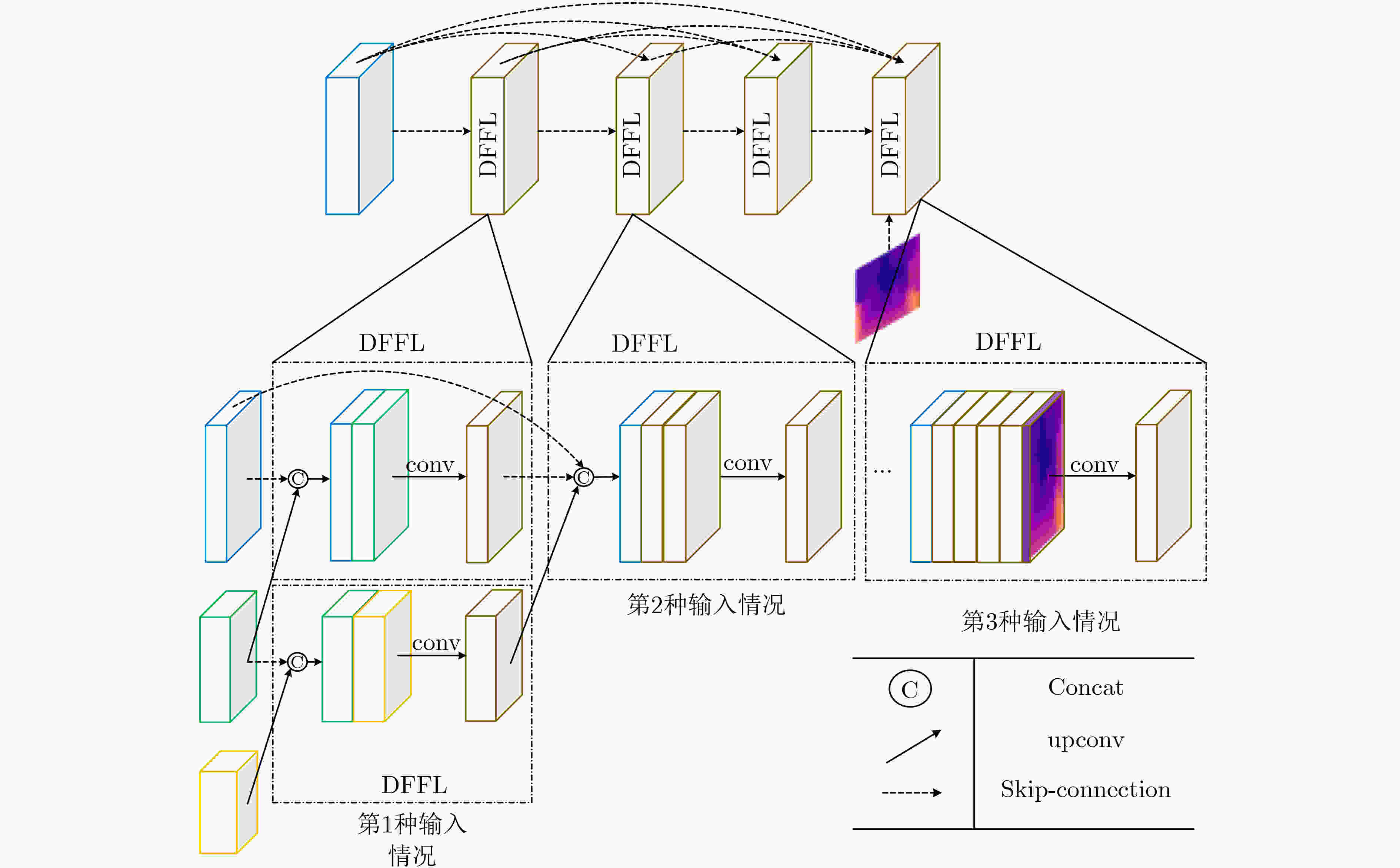
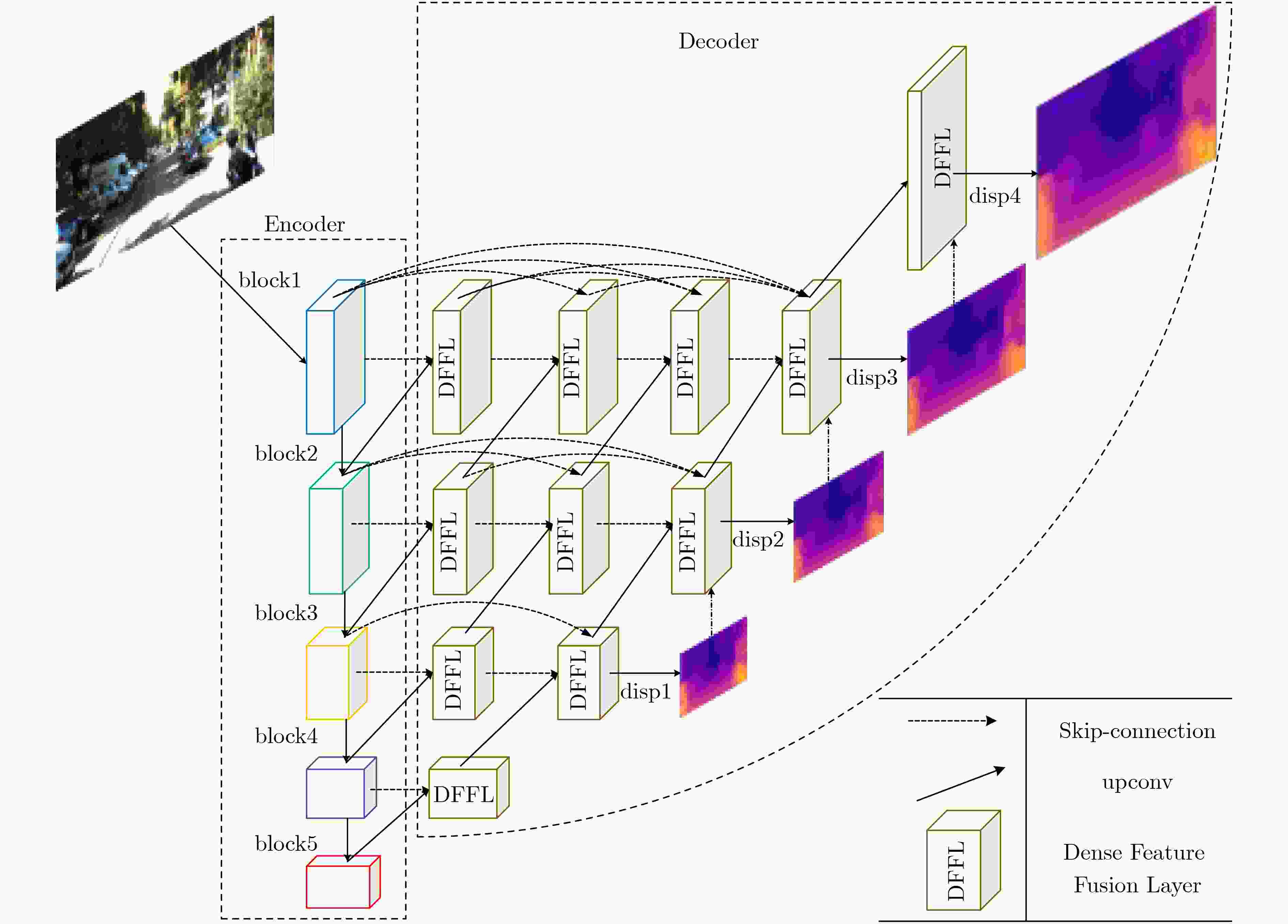
摘要: 针对无监督单目深度估计生成深度图质量低、边界模糊、伪影过多等问题，该文提出基于密集特征融合的深度网络编解码结构。设计密集特征融合层(DFFL)并将其以密集连接的形式填充U型编解码器，同时精简编码器部分，实现编、解码器的性能均衡。在训练过程中，将校正后的双目图像输入给网络，以重构视图的相似性约束网络生成视差图。测试时，根据已知的相机基线距离与焦距将生成的视差图转换为深度图。在KITTI数据集上的实验结果表明，该方法在预测精度和误差值上优于现有的算法。
- 深度估计 /
- 无监督 /
- 密集特征融合层 /
- 编解码器
Abstract: In view of the problems of low quality, blurred borders and excessive artifacts generated by unsupervised monocular depth estimation, a deep network encoder-decoder structure based on dense feature fusion is proposed. A Dense Feature Fusion Layer(DFFL) is designed and it is filled with U-shaped encoder-decoder in the form of dense connection, while simplifying the encoder part to achieve a balanced performance of the encoder and decoder. During the training process, the calibrated stereo pair is input to the network to constrain the network to generate disparity maps by the similarity of reconstructed views. During the test process, the generated disparity map is converted into a depth map based on the known camera baseline distance and focal length. The experimental results on the KITTI data set show that this method is superior to the existing algorithms in terms of prediction accuracy and error value.
- Depth estimation /
- Unsupervised learning /
- Dense Feature Fusion Layer(DFFL) /
- Encoder-decoder

HTML全文

图 1 无监督深度估计算法框图

下载: 全尺寸图片幻灯片

图 2 U-Net, U-Net++和本文的网络拓扑图

下载: 全尺寸图片幻灯片

图 3 密集特征融合层及其密集连接

下载: 全尺寸图片幻灯片

图 4 网络框架

下载: 全尺寸图片幻灯片

图 5 KITTI数据集上可视化结果对比

下载: 全尺寸图片幻灯片

表 1 修改前后的编码器参数

层	R50	PR50
block1	7×7,64,stride2	$\left[ {\begin{array}{*{20}{c}}{1 \times 1,8}\\{3 \times 3,8}\\{1 \times 1,32}\end{array}} \right] \times 2$
block2_x	3×3 max pool,stride2, $\left[ {\begin{array}{*{20}{c}}{1 \times 1,64}\\{3 \times 3,64}\\{1 \times 1,256}\end{array}} \right]$×3	$\left[ {\begin{array}{*{20}{c}}{1 \times 1,32}\\{3 \times 3,32}\\{1 \times 1,128}\end{array}} \right]$×3
block3_x	$\left[ {\begin{array}{*{20}{c}}{1 \times 1,128}\\{3 \times 3,128}\\{1 \times 1,512}\end{array}} \right]$×4	$\left[ {\begin{array}{*{20}{c}}{1 \times 1,64}\\{3 \times 3,64}\\{1 \times 1,256}\end{array}} \right]$×4
block4_x	$\left[ {\begin{array}{*{20}{c}}{1 \times 1,256}\\{3 \times 3,256}\\{1 \times 1,1024}\end{array}} \right]$×6	$\left[ {\begin{array}{*{20}{c}}{1 \times 1,128}\\{3 \times 3,128}\\{1 \times 1,512}\end{array}} \right]$×6
block5_x	$\left[ {\begin{array}{*{20}{c}}{1 \times 1,512}\\{3 \times 3,512}\\{1 \times 1,2048}\end{array}} \right]$×3	$\left[ {\begin{array}{*{20}{c}}{1 \times 1,256}\\{3 \times 3,256}\\{1 \times 1,1024}\end{array}} \right]$×3

下载: 导出CSV

表 2 KITTI数据集使用Eigen拆分集的验证结果

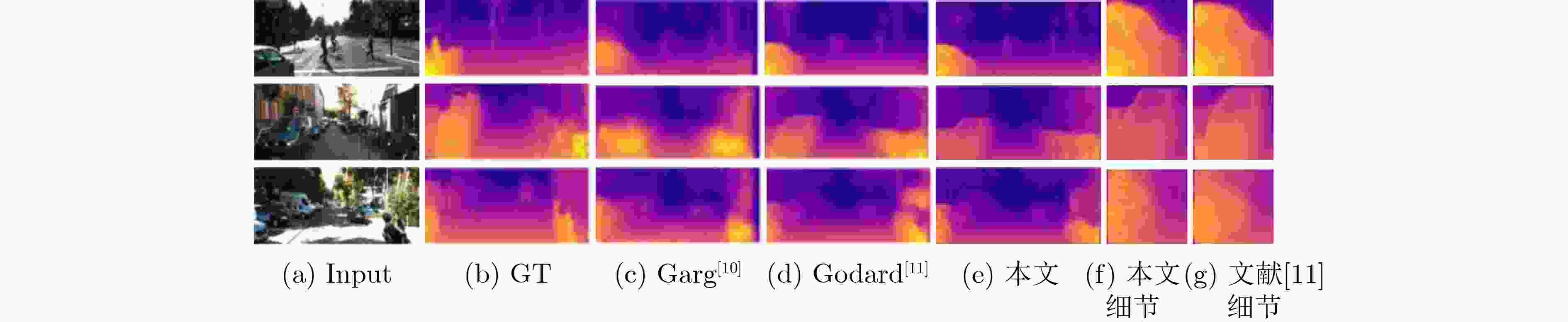
方法	监督方式	越小越好				越大越好
方法	监督方式	Abs Rel	Sq Rel	RMSE	RMSE ln	$\delta < 1.25$	$\delta < {1.25^2}$	$\delta < {1.25^3}$
Eigen^[3]	D	0.203	1.548	6.307	0.282	0.702	0.890	0.890
Liu^[4]	D	0.201	1.584	6.471	0.273	0.680	0.898	0.967
Klodt^[19]	D+M	0.166	1.490	5.998	–	0.778	0.919	0.966
Zhou^[9]	M	0.183	1.595	6.709	0.270	0.734	0.902	0.959
Struct2depth^[20]	M	0.141	1.026	5.291	0.215	0.816	0.945	0.979
Garg^[10]	S	0.152	1.226	5.849	0.246	0.784	0.921	0.967
StrAT^[21]	S	0.128	1.019	5.403	0.227	0.827	0.935	0.971
Monodepth2^[22]	S	0.130	1.144	5.485	0.232	0.831	0.932	0.968
Monodepth+pp^[11]	S	0.128	1.038	5.355	0.223	0.833	0.939	0.972
3Net+pp^[23]	S	0.126	0.961	5.205	0.220	0.835	0.941	0.974
本文	S	0.131	1.110	5.426	0.224	0.839	0.941	0.972
本文+pp	S	0.122	0.939	5.063	0.212	0.850	0.947	0.976

下载: 导出CSV

表 3 KITTI数据集消融实验的结果

方法	编码器网络	参数量(×10⁶)	Abs Rel	$\delta < 1.25$	预测速度(fps)
Baseline	R50	58.5	0.143	0.812	21
Baseline+DFFL	R50	158.0	0.135	0.833	11
网络修剪+DFFL	PR50	39.4	0.131	0.839	21
Baseline	R18	20.2	0.149	0.794	46
Baseline+DFFL	R18	20.4	0.139	0.820	22
网络修剪+DFFL	PR18	19.1	0.129	0.835	33

下载: 导出CSV

表 4 3种输入下消融实验的结果

方法	编码器网络	Abs Rel	$\delta < 1.25$
Baseline	PR50	0.137	0.821
Baseline +DFFL (第1种输入)	PR50	0.161	0.828
Baseline +DFFL (第2种输入)	PR50	0.132	0.836
Baseline +DFFL (第3种输入)	PR50	0.131	0.839

下载: 导出CSV

参考文献(23)

[1]	SNAVELY N, SEITZ S M, and SZELISKI R. Skeletal graphs for efficient structure from motion[C]. 2008 IEEE Conference on Computer Vision and Pattern Recognition, Anchorage, USA, 2008: 1–8.
[2]	狄红卫, 柴颖, 李逵. 一种快速双目视觉立体匹配算法[J]. 光学学报, 2009, 29(8): 2180–2184. doi: 10.3788/AOS20092908.2180 DI Hongwei, CHAI Ying, and LI Kui. A fast binocular vision stereo matching algorithm[J]. Acta Optica Sinica, 2009, 29(8): 2180–2184. doi: 10.3788/AOS20092908.2180
[3]	EIGEN D, PUHRSCH C, and FERGUS R. Depth map prediction from a single image using a multi-scale deep network[C]. The 27th International Conference on Neural Information Processing Systems, Montreal, Canada, 2014: 2366–2374.
[4]	LIU Fayao, SHEN Chunhua, LIN Guosheng, et al. Learning depth from single monocular images using deep convolutional neural fields[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2016, 38(10): 2024–2039. doi: 10.1109/TPAMI.2015.2505283
[5]	LAINA I, RUPPRECHT C, BELAGIANNIS V, et al. Deeper depth prediction with fully convolutional residual networks[C]. The 2016 4th International Conference on 3D Vision, Stanford, USA, 2016: 239–248.
[6]	HE Kaiming, ZHANG Xiangyu, REN Shaoqing, et al. Deep residual learning for image recognition[C]. 2016 IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, USA, 2016: 770–778.
[7]	周武杰, 潘婷, 顾鹏笠, 等. 基于金字塔池化网络的道路场景深度估计方法[J]. 电子与信息学报, 2019, 41(10): 2509–2515. doi: 10.11999/JEIT180957 ZHOU Wujie, PAN Ting, GU Pengli, et al. Depth estimation of monocular road images based on pyramid scene analysis network[J]. Journal of Electronics &Information Technology, 2019, 41(10): 2509–2515. doi: 10.11999/JEIT180957
[8]	ZHAO Shanshan, FU Huan, GONG Mingming, et al. Geometry-aware symmetric domain adaptation for monocular depth estimation[C]. 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, USA, 2019: 9780–9790.
[9]	ZHOU Tinghui, BROWN M, SNAVELY N, et al. Unsupervised learning of depth and ego-motion from video[C]. 2017 IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, USA, 2017: 6612–6619.
[10]	GARG R, B G V K, CARNEIRO G, et al. Unsupervised CNN for single view depth estimation: Geometry to the rescue[C]. The 14th European Conference on Computer Vision, Amsterdam, The Netherlands, 2016: 740–756.
[11]	GODARD C, MAC AODHA O, and BROSTOW G J. Unsupervised monocular depth estimation with left-right consistency[C]. 2017 IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, USA, 2017: 6602–6611.
[12]	ZHOU Zongwei, SIDDIQUEE M R, TAJBAKHSH N, et al. UNet++: Redesigning skip connections to exploit multiscale features in image segmentation[J]. IEEE Transactions on Medical Imaging, 2020, 39(6): 1856–1867. doi: 10.1109/TMI.2019.2959609
[13]	GEIGER A, LENZ P, and URTASUN R. Are we ready for autonomous driving? The KITTI vision benchmark suite[C]. 2012 IEEE Conference on Computer Vision and Pattern Recognition, Providence, USA, 2012: 3354–3361.
[14]	HARTLEY R and ZISSERMAN A. Multiple View Geometry in Computer Vision[M]. 2nd ed. New York: Cambridge University Press, 2003: 262–263.
[15]	RONNEBERGER O, FISCHER P, and BROX T. U-net: Convolutional networks for biomedical image segmentation[C]. The 18th International Conference on Medical Image Computing and Computer-Assisted Intervention, Munich, Germany, 2015: 234–241.
[16]	HUANG Gao, LIU Zhuang, VAN DER MAATEN L, et al. Densely connected convolutional networks[C]. 2017 IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, USA, 2017: 2261–2269.
[17]	SZEGEDY C, VANHOUCKE V, IOFFE S, et al. Rethinking the inception architecture for computer vision[C]. 2016 IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, USA, 2016: 2818–2826.
[18]	WANG Zhou, BOVIK A C, SHEIKH H R, et al. Image quality assessment: From error visibility to structural similarity[J]. IEEE Transactions on Image Processing, 2004, 13(4): 600–612. doi: 10.1109/TIP.2003.819861
[19]	KLODT M and VEDALDI A. Supervising the new with the old: Learning SFM from SFM[C]. The 15th European Conference on Computer Vision, Munich, Germany, 2018: 713–728.
[20]	CASSER V, PIRK S, MAHJOURIAN R, et al. Depth prediction without the sensors: Leveraging structure for unsupervised learning from monocular videos[C]. The 33rd AAAI Conference on Artificial Intelligence, Honolulu, USA, 2019: 8001–8008.
[21]	MEHTA I, SAKURIKAR P, and NARAYANAN P J. Structured adversarial training for unsupervised monocular depth estimation[C]. 2018 International Conference on 3D Vision, Verona, Italy, 2018: 314–323.
[22]	GODARD C, MAC AODHA O, FIRMAN M, et al. Digging into self-supervised monocular depth estimation[C]. 2019 IEEE/CVF International Conference on Computer Vision, Seoul, Korea (South), 2019: 3827–3837.
[23]	POGGI M, TOSI F, and MATTOCCIA S. Learning monocular depth estimation with unsupervised trinocular assumptions[C]. 2018 International Conference on 3D Vision, Verona, Italy, 2018: 324–333.