An Image Encryption Algorithm Based on Logistic Chaotic Mapping with Sinusoidal Feedback and Its FPGA Implementation
-
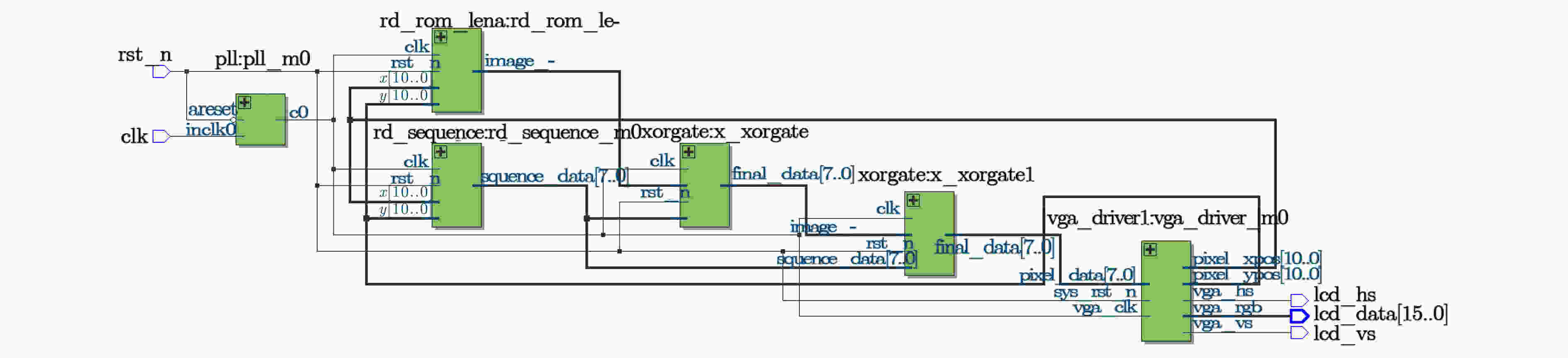
摘要: 基于混沌的数字图像加密算法因具有较大的密钥空间和较高的密钥敏感特性等而被广泛地应用。该文在经典Logistic映射中引入正弦反馈,构成新的映射关系,并分析该映射的混沌行为。利用混沌映射导出离散混沌加密序列,并对加密序列进行放大取整,增强其伪随机性;利用NIST随机性测试方法测试了加密序列的伪随机性;将伪随机序列与原始图像进行异或运算,实现图像加密。数值仿真结果表明所提加密算法具有较好的加密效果,其密钥也具有较好的敏感性和伪随机性,最后基于FPGA平台的硬件加密实现了本算法。
-
关键词:
- 图像加密 /
- Logistic混沌映射 /
- 正弦反馈 /
- FPGA /
- NIST
Abstract: Digital image encryption algorithm based on chaos is widely used because of its large key space and high key sensitivity. The sinusoidal feedback is introduced into the classical Logistic mapping to form a new discrete mapping, and the chaotic behavior of the mapping is analyzed. The chaotic mapping is used to derive the discrete chaotic encryption sequence, and the encryption sequence is enlarged and rounded to enhance its pseudo-randomness. The pseudo-randomness of encrypted sequences is tested by NIST (National Institute of Standards and Technology) test method. The pseudo-random sequence is XOR (Exclusive OR) with the original image to realize image encryption. Numerical simulation results show that the new encryption algorithm has better encryption effect, and its key shows better sensitivity and pseudo-randomness. Finally, hardware encryption for this algorithm is realized based on FPGA (Field Programmable Gate Array) platform. -
表 1 NIST标准伪随机测试结果
测试编号 测试名称 P_value 测试通过率(%) 1 频率(单比特)测试 0.964290 99 2 块内频数测试 0.181557 100 3 游程测试 0.401199 99 4 块内最大游程测试 0.779188 100 5 二元矩阵秩测试 0.004981 100 6 频谱测试 0.304126 100 7 非重叠字匹配测试 0.534146 97 8 重叠字匹配测试 0.213390 99 9 Maurer通用统计检测 0.178278 100 10 线性复杂度测试 0.262249 98 11 系列测试 0.058984 99 12 近似熵测试 0.178876 100 13 累积和测试 0.816537 98 14 随机游程测试 0.535328 所有数据为一个数据块,大小为30 MB,不计通过率 15 随机游程变量测试 0.532553 表 2 信息熵实验结果
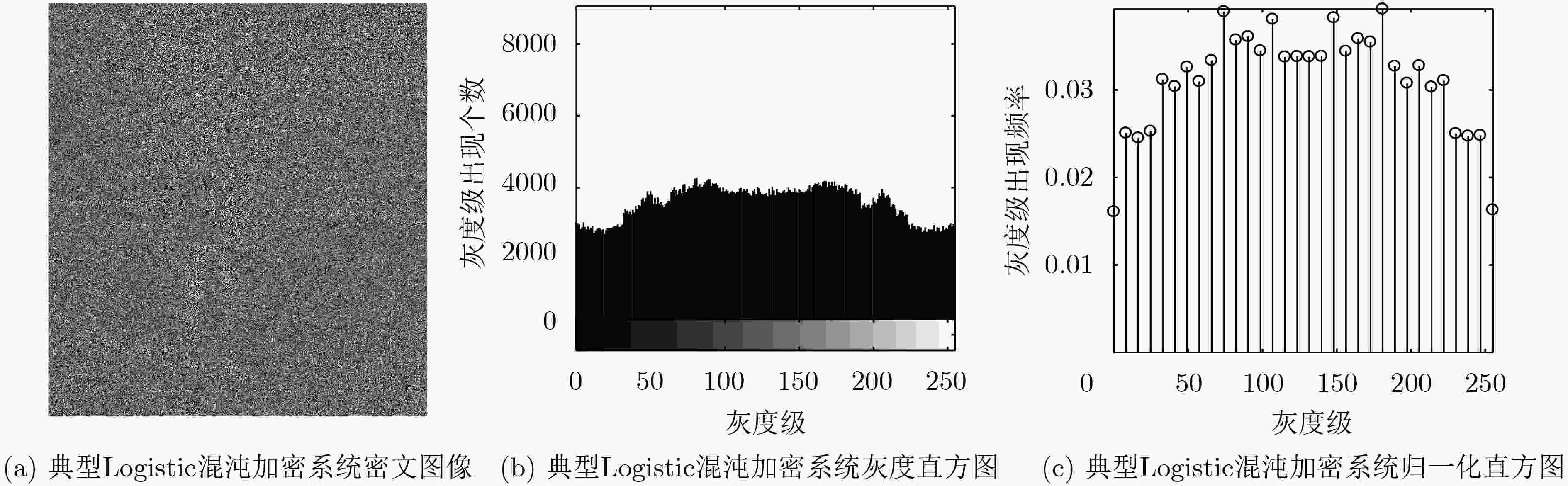
明文 密文 7.6005 7.9987 表 3 图像的相邻像素相关性
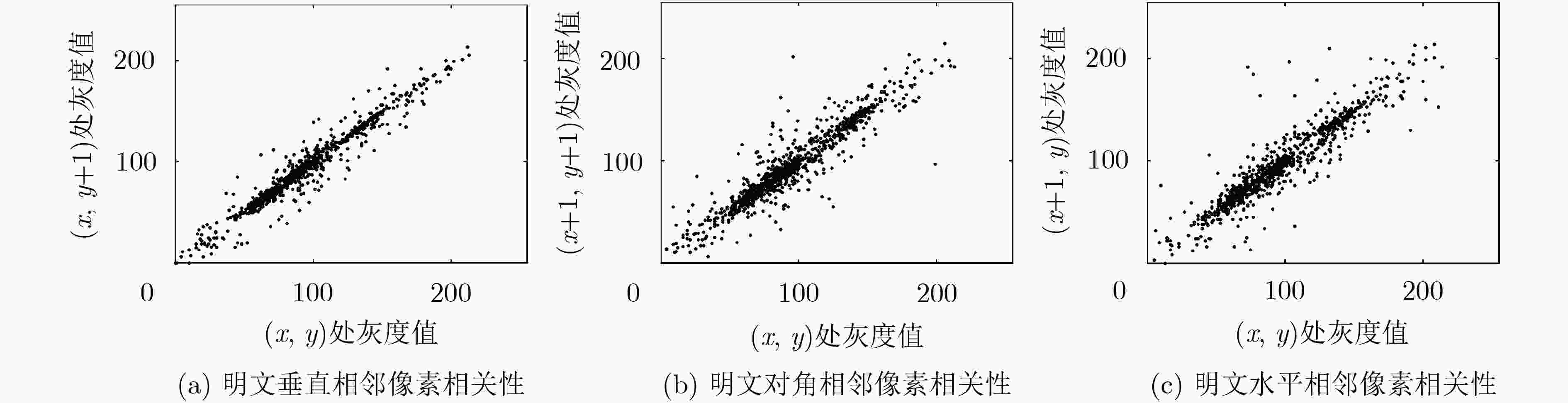
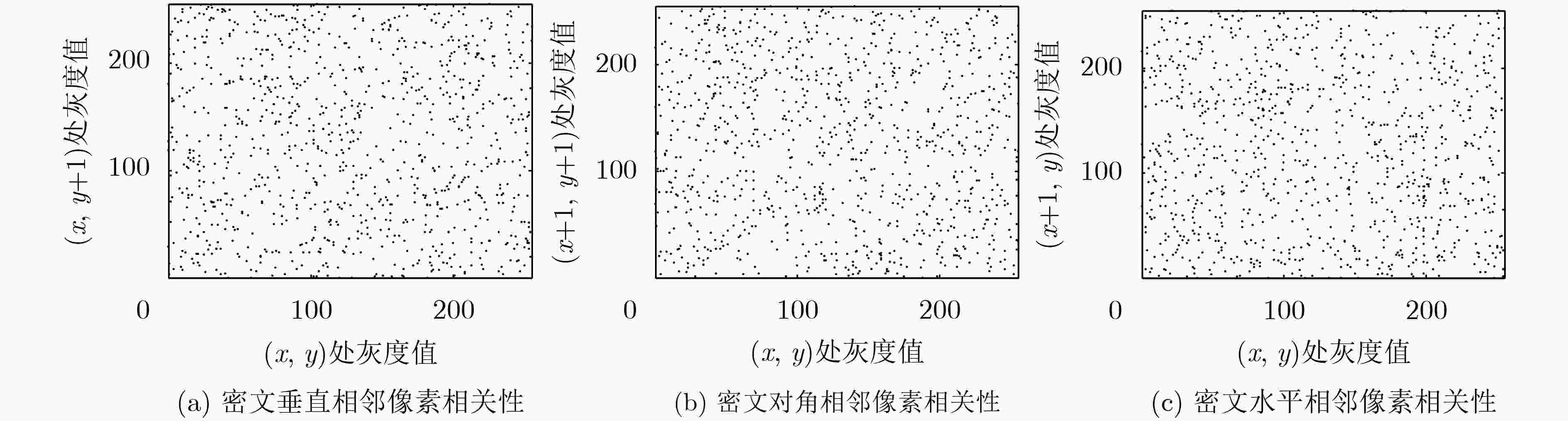
图像 水平 垂直 对角线 Lena 明文 0.9765 0.9597 0.9420 密文 –0.0082 –0.0054 0.0020 -
[1] LI Chengqing, ZHANG Yun, Xie E Y. When an attacker meets a cipher-image in 2018: A year in review[J]. Journal of Information Security and Applications, 2019, 48: 102361. doi: 10.1016/j.jisa.2019.102361 [2] 张慧奔. 基于混沌图像加密算法的研究[D]. [硕士论文], 电子科技大学, 2015.ZHANG Huiben. Chaotic image encryption algorithm research[D]. [Master dissertation], University of Electronic Science and Technology of China, 2015. [3] YOON J W and KIM H. An image encryption scheme with a pseudorandom permutation based on chaotic maps[J]. Communications in Nonlinear Science and Numerical Simulation, 2010, 15(12): 3998–4006. doi: 10.1016/j.cnsns.2010.01.041 [4] PENG Yuexi, SUN Kehui, and HE Shaobo. Dynamics analysis of chaotic maps: From perspective on parameter estimation by meta-heuristic algorithm[J]. Chinese Physics B, 2020, 29(3): 030502. doi: 10.1088/1674-1056/ab695c [5] 徐红梅, 郭树旭. 基于符号相对熵的Logistic混沌系统时间不可逆性分析[J]. 电子与信息学报, 2014, 36(5): 1242–1246. doi: 10.3724/SP.J.1146.2013.01262XU Hongmei and GUO Shuxu. Time irreversibility analysis of logistic chaos system based on symbolic relative entropy[J]. Journal of Electronics &Information Technology, 2014, 36(5): 1242–1246. doi: 10.3724/SP.J.1146.2013.01262 [6] 郑继明, 汤智睿, 邓建秀, 等. 基于Logistic混沌映射的数字图像加密算法[J]. 科技与创新, 2018(18): 8–11. doi: 10.15913/j.cnki.kjycx.2018.18.008ZHEN Jiming, TANG Zhirui, DENG Jianxiu, et al. Digital image encryption algorithm based on Logistic chaotic map[J]. Science and Technology &Innovation, 2018(18): 8–11. doi: 10.15913/j.cnki.kjycx.2018.18.008 [7] 陈志刚, 梁涤青, 邓小鸿, 等. Logistic混沌映射性能分析与改进[J]. 电子与信息学报, 2016, 38(6): 1547–1551. doi: 10.11999/JEIT151039CHEN Zhigang, LIANG Diqing, DENG Xiaohong, et al. Performance analysis and improvement of Logistic chaotic mapping[J]. Journal of Electronics &Information Technology, 2016, 38(6): 1547–1551. doi: 10.11999/JEIT151039 [8] 陶红. 基于Logistic混沌序列的图像加密设计[D]. [硕士论文], 东南大学, 2018.TAO Hong. Design of image encryption algorithm based on Logistic chaotic sequence[D]. [Master dissertation], Southeast University, 2018. [9] 齐红涛, 苏涛. 基于FPGA的高速AD采样设计[J]. 航空兵器, 2010(1): 35–39. doi: 10.19297/j.cnki.41-1228/tj.2010.01.009QI Hongtao and SU Tao. Design of high AD sampling based on FPGA[J]. AERO Weaponry, 2010(1): 35–39. doi: 10.19297/j.cnki.41-1228/tj.2010.01.009 [10] MAY R M. Simple mathematical models with very complicated dynamics[J]. Nature, 1976, 261(5560): 459–467. doi: 10.1038/261459a0 [11] 高智中, 李会芳. Logistic的混沌分析及其控制[J]. 运城学院学报, 2006, 24(2): 12–14. doi: 10.15967/j.cnki.cn14-1316/g4.2006.02.006GAO Zhizhong and LI Huifang. Chaos analysis and chaos controlling of Logistic map[J]. Journal of Yuncheng University, 2006, 24(2): 12–14. doi: 10.15967/j.cnki.cn14-1316/g4.2006.02.006 [12] 张双红. Logistic模型的Matlab计算与可视化[J]. 吉林师范大学学报: 自然科学版, 2009, 30(3): 97–99. doi: 10.16862/j.cnki.issn1674-3873.2009.03.024ZHANG Shuanghong. Calculation and visualization of Logistic model by using Matlab[J]. Jilin Normal University Journal:Natural Science Edition, 2009, 30(3): 97–99. doi: 10.16862/j.cnki.issn1674-3873.2009.03.024 [13] 罗利军, 李银山, 李彤, 等. 李雅普诺夫指数谱的研究与仿真[J]. 计算机仿真, 2005, 22(12): 285–288. doi: 10.3969/j.issn.1006-9348.2005.12.080LUO Lijun, LI Yinshan, LI Tong, et al. Research and simulation of Lyapunov’s exponents[J]. Computer Simulation, 2005, 22(12): 285–288. doi: 10.3969/j.issn.1006-9348.2005.12.080 [14] 毛骁骁, 孙克辉, 刘文浩. 基于分数阶统一混沌系统的图像加密算法[J]. 传感器与微系统, 2017, 36(6): 138–141. doi: 10.13873/j.1000-9787(2017)06-0138-04MAO Xiaoxiao, SUN Kehui, and LIU Wenhao. Image encryption algorithm based on fractional order unified chaotic system[J]. Transducer and Microsystem Technologies, 2017, 36(6): 138–141. doi: 10.13873/j.1000-9787(2017)06-0138-04 [15] 李付鹏, 刘敬彪, 王光义, 等. 基于混沌集的图像加密算法[J]. 电子与信息学报, 2020, 42(4): 981–987. doi: 10.11999/JEIT190344LI Fupeng, LIU Jingbiao, WANG Guangyi, et al. An image encryption algorithm based on chaos set[J]. Journal of Electronics &Information Technology, 2020, 42(4): 981–987. doi: 10.11999/JEIT190344 [16] 马上, 刘剑锋, 杨泽国, 等. 基于余数系统与置换多项式的高速长周期伪随机序列生成方法[J]. 电子与信息学报, 2018, 40(1): 42–49. doi: 10.11999/JEIT170421MA Shang, LIU Jianfeng, YANG Zeguo, et al. A method of generating high speed and long period pseudo-random sequence based on residue number system and permutation polynomial[J]. Journal of Electronics &Information Technology, 2018, 40(1): 42–49. doi: 10.11999/JEIT170421 [17] 肖成龙, 孙颖, 林邦姜, 等. 基于神经网络与复合离散混沌系统的双重加密方法[J]. 电子与信息学报, 2020, 42(3): 687–694. doi: 10.11999/JEIT190213XIAO Chenglong, SUN Ying, LIN Bangjiang, et al. Double encryption method based on neural network and composite discrete chaotic system[J]. Journal of Electronics &Information Technology, 2020, 42(3): 687–694. doi: 10.11999/JEIT190213 [18] 郭媛, 周艳艳, 敬世伟. 基于图像重组和比特置乱的多图像加密[J]. 光子学报, 2020, 49(4): 0410002. doi: 10.3788/gzxb20204904.0410002GUO Yuan, ZHOU Yanyan, and JING Shiwei. Multiple-image encryption based on image recombination and bit scrambling[J]. Acta Photonica Sinica, 2020, 49(4): 0410002. doi: 10.3788/gzxb20204904.0410002 [19] 刘旭. 基于深度学习对一类混沌图像加密算法进行安全性分析[D]. [硕士论文], 南京邮电大学, 2019.LIU Xu. Security analysis of a class of chaotic image encryption algorithm based on deep learning[D]. [Master dissertation], Nanjing University of Posts and Telecommunications, 2019. [20] 向滔. 基于混沌的数字图像加密算法的分析与设计[D]. [硕士论文], 重庆大学, 2014.XIANG Tao. Analysis and designs of digital image encryption algorithm based on chaos[D]. [Master dissertation], Chongqing University, 2014. -





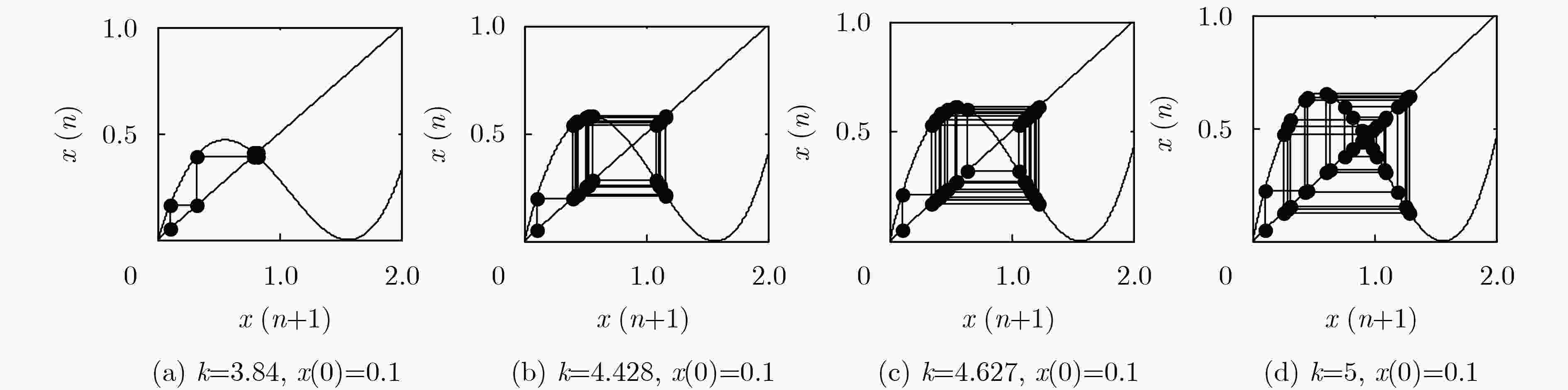
 下载:
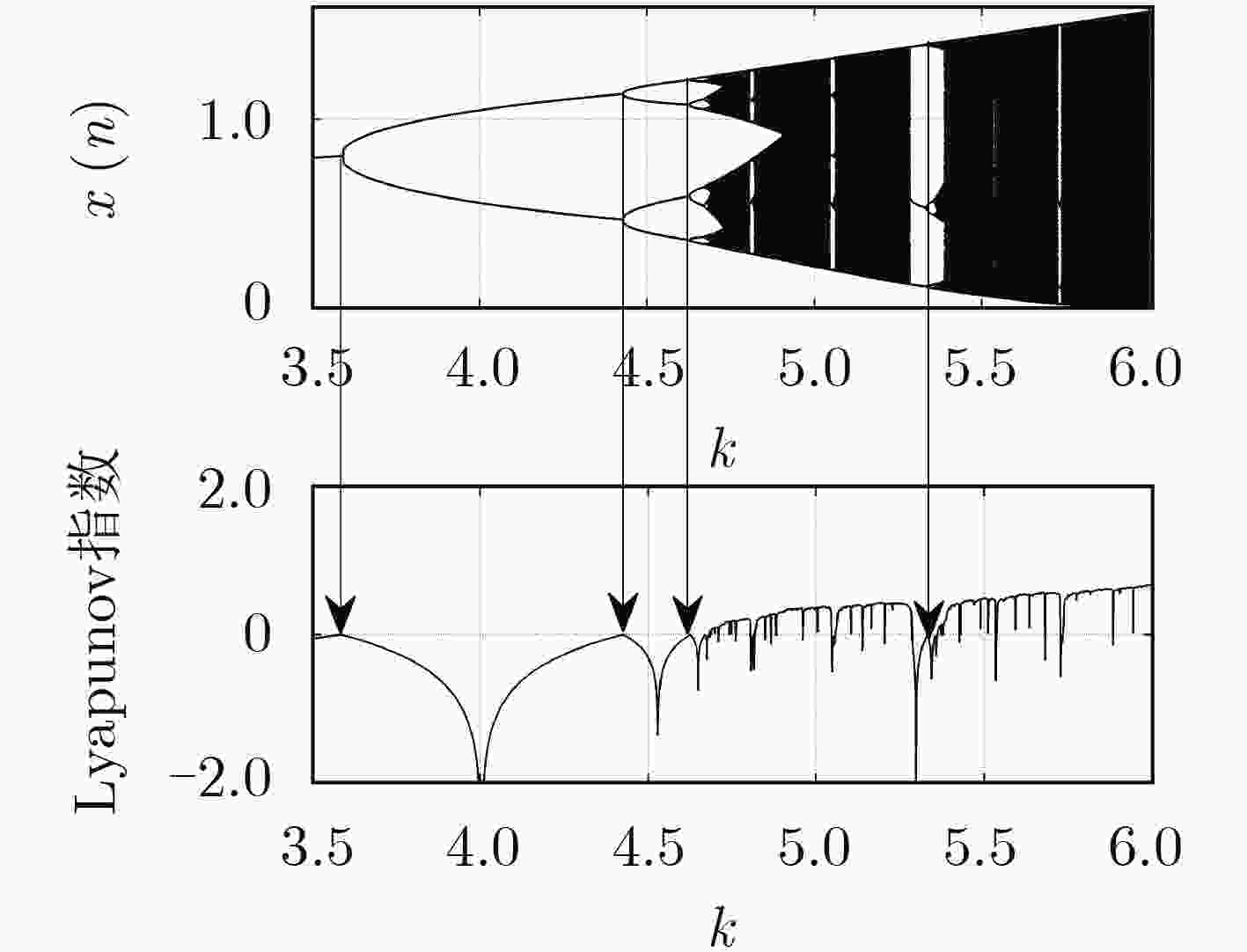
下载:
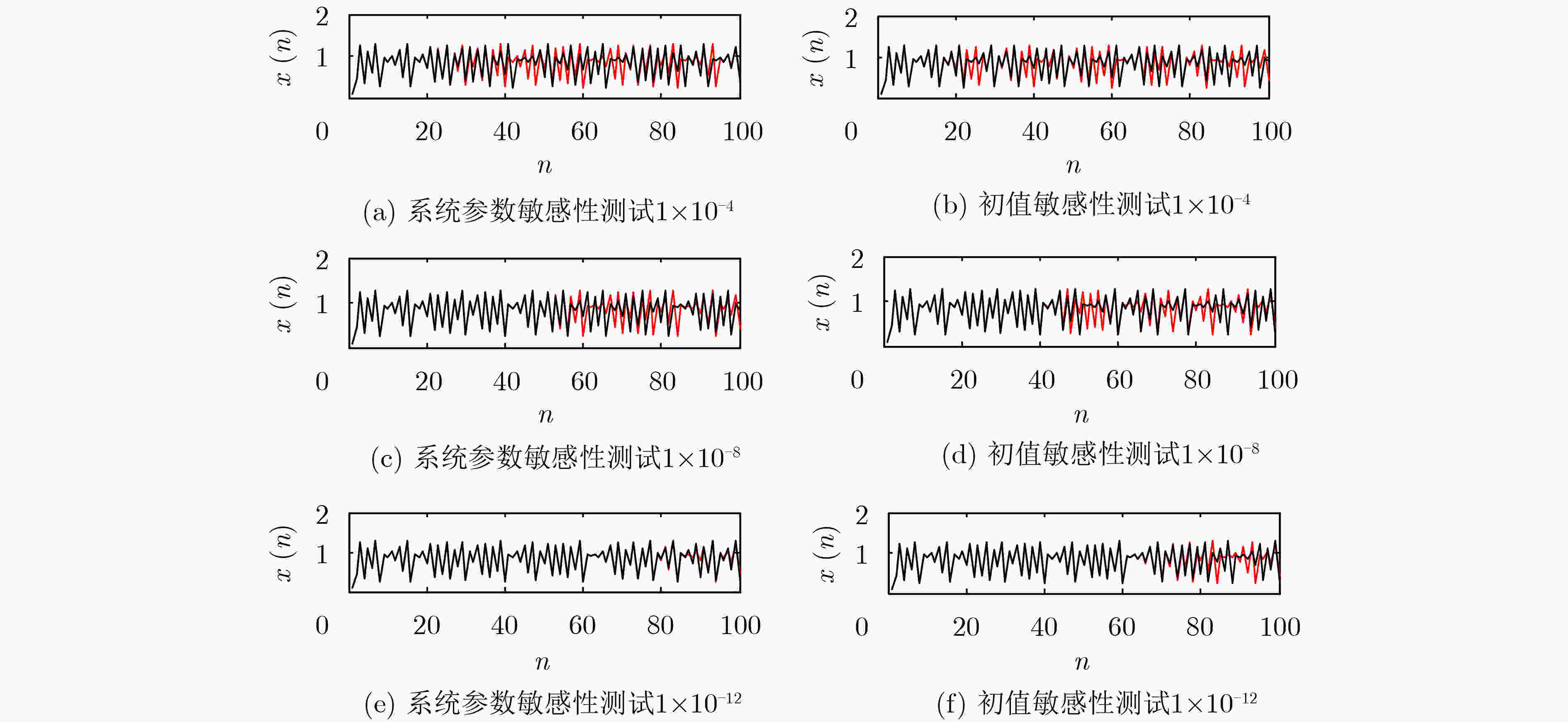

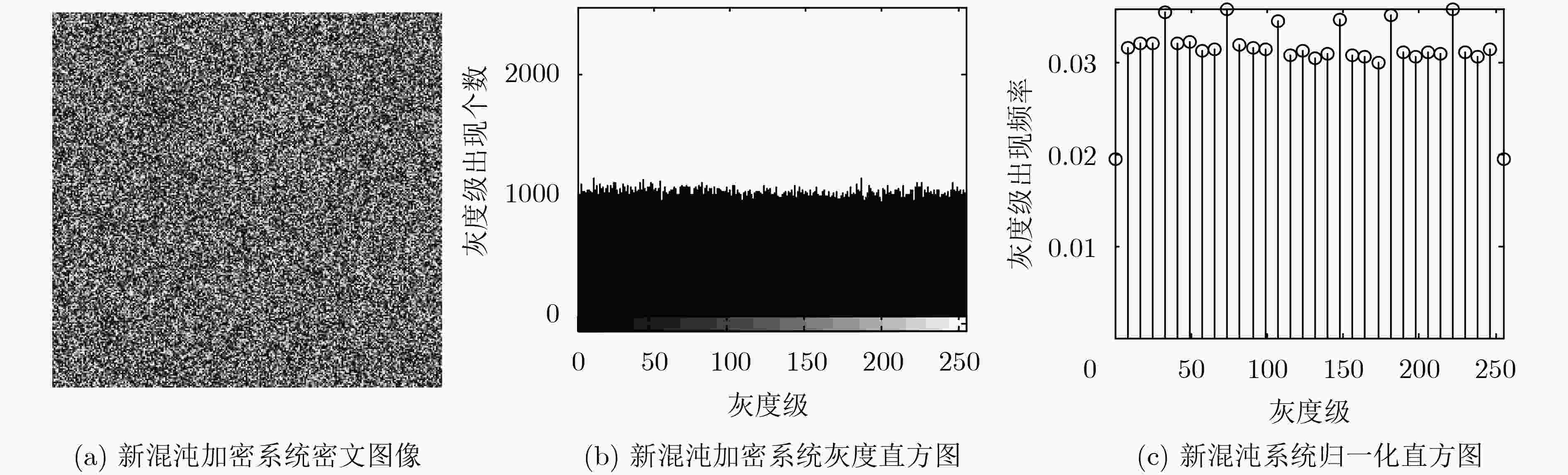











 下载:
下载:
