Blind Synchronization and Estimation for PN Code of NPLC-DSSS Signal
-
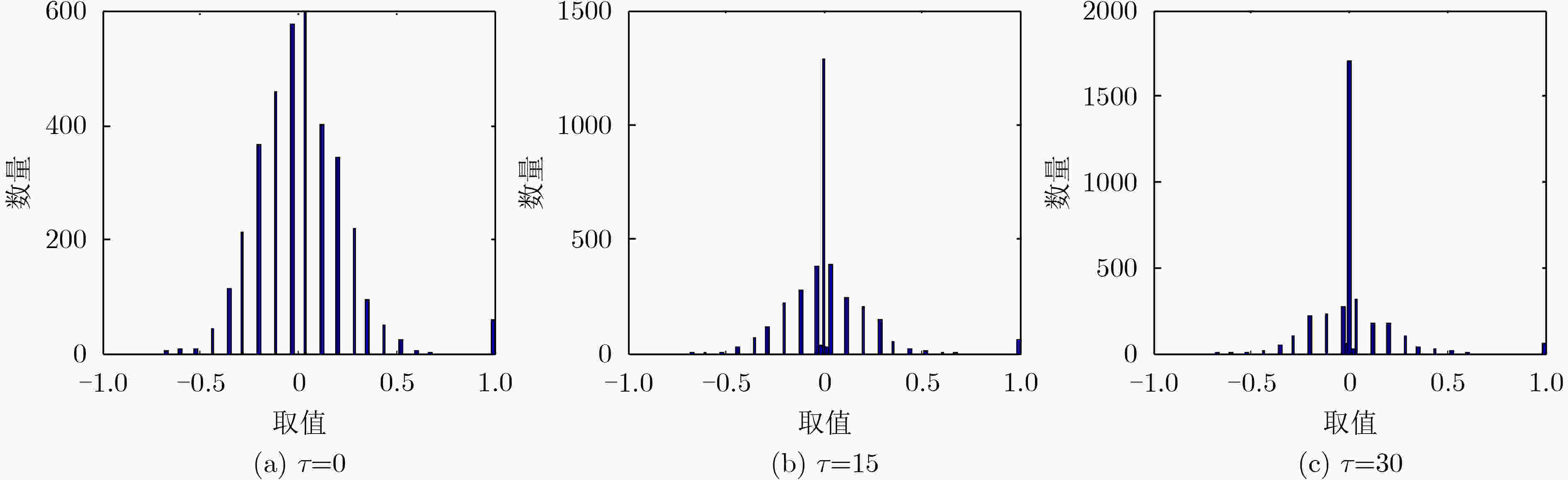
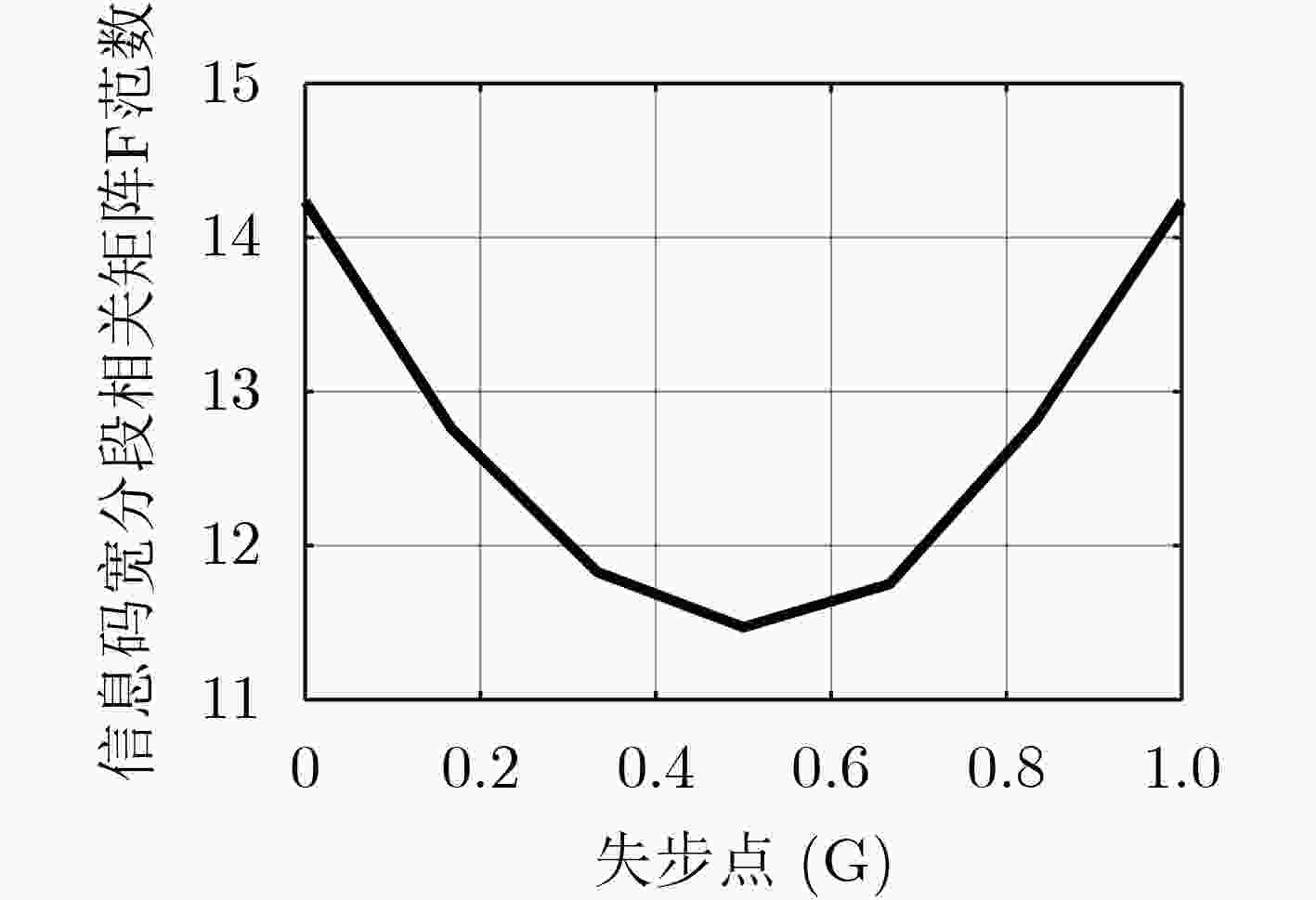
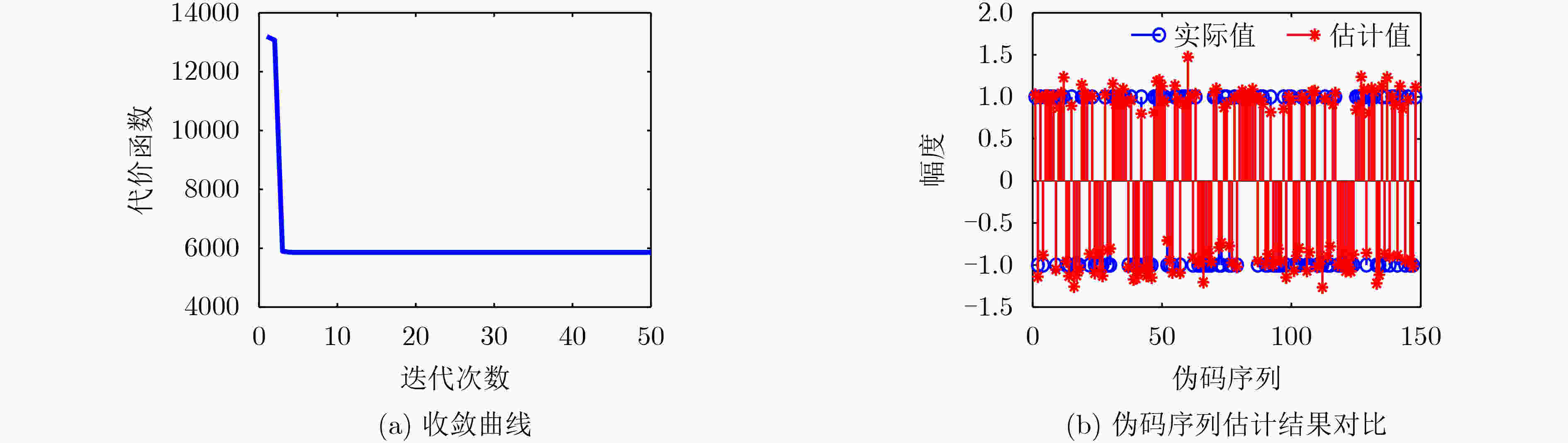
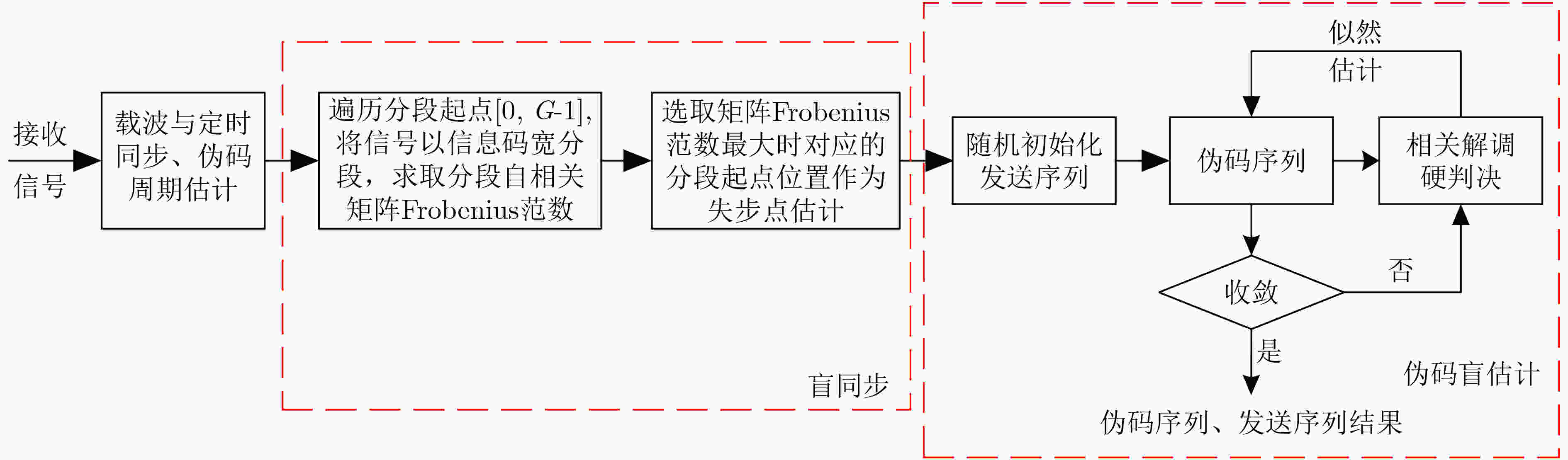
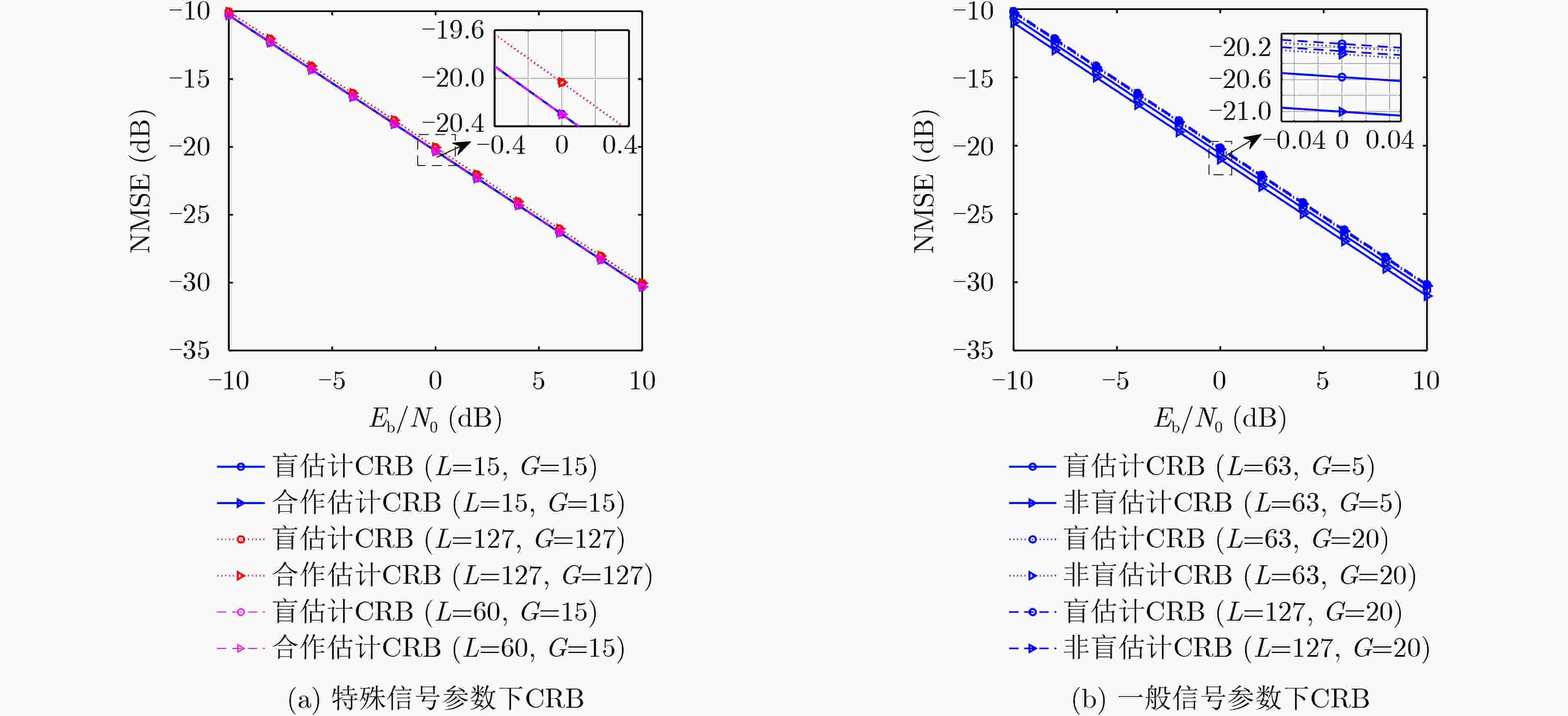
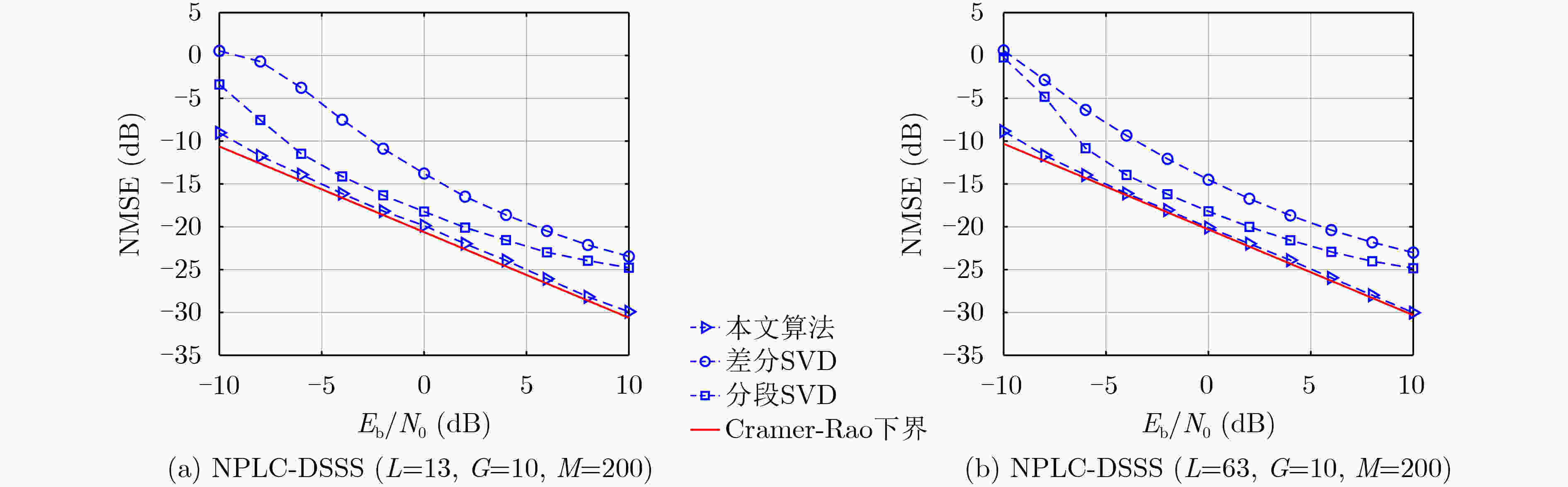
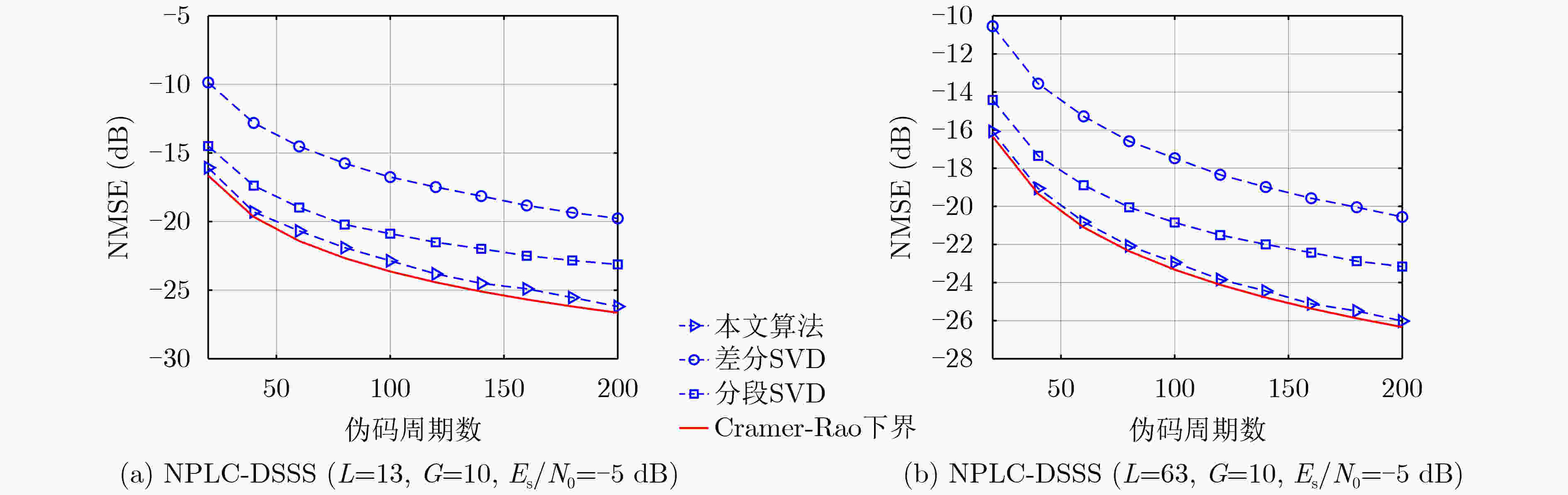
摘要: 非合作直接序列扩频系统中伪随机码的估计与同步是正确获取信息的关键。现有的研究成果多集中在短码或周期长码直扩信号的解扩,该文针对无伪码先验知识条件下NPLC-DSSS信号的失步时间估计问题,提出一种基于相关矩阵元素分布建模的方法,该方法以信息码宽分段的信号构建自相关矩阵,并以该矩阵的Frobenius 范数与失步时间之间的对应关系,实现NPLC-DSSS信号失步时间的精确估计。在此基础上,通过引入判决辅助思想构建了循环迭代结构实现了NPLC-DSSS信号伪码序列的盲估计。最后,推导了该伪码序列盲估计问题的Cramer-Rao理论界。数值分析结果表明,文中所述算法在相同的信噪比和数据量条件下具有更好的估计精度,且对伪码的估计性能接近理论界。Abstract: Synchronization and estimation for Pseudo Noise (PN) code of non-cooperative Direct Sequence Spread Spectrum(DSSS)system is the key to obtain the information correctly. Previous works mostly concentrate on Short or Periodic Long Code DSSS(SC-DSSS, PLC-DSSS)signal. Aiming at the estimation for out-of-step time of Non-Periodic Long Code DSSS (NPLC-DSSS) signal without the prior knowledge about the PN code, a distribution modeling-based method for the elements of correlation matrix is proposed. The auto-correlation matrix of information-bit-long segments is constructed and the accurate estimation for out-of-step time is achieved according to the Frobenius norm as a function of out-of-step time. On this basis, by introducing decision aided idea, the cyclic iterative structure is constructed to realize a blind estimation for PN sequence of NPLC-DSSS signal. Finally, the Cramer-Rao Bound (CRB) for the blind PN code estimation problem is derived. Numerical analysis results demonstrate that the proposed method can achieve better estimation accuracy in the same signal to noise ratio and data volume condition and the performance is close to the theoretical bound.
-
表 1 实验信号参数
信号1 信号2 伪码周期 13 63 生成多项式 $f(x) = {x^4} + x + 1$ $f(x) = {x^6} + x + 1$ 伪码序列初态 $\left[ {1\;0\;0\;1} \right] $ $\left[ {1\;0\;1\;0\;1\;1} \right] $ 信息码宽 10 10 信噪比 –10~10 dB –10~10 dB 数据量 200(/伪码周期) 200(/伪码周期) 失步时间 随机 随机 -
[1] COOK C E and MARSH H S. An introduction to spread spectrum[J]. IEEE Communications Magazine, 1983, 21(2): 8–16. doi: 10.1109/MCOM.1983.1091346 [2] QU Fengzhong, QIN Xiangzhao, YANG Liuqing, et al. Spread-spectrum method using multiple sequences for underwater acoustic communications[J]. IEEE Journal of Oceanic Engineering, 2018, 43(4): 1215–1226. doi: 10.1109/JOE.2017.2750298 [3] 谢岸宏, 朱立东, 翟继强, 等. 一种抗盲检测的直扩隐蔽信号设计方法[J]. 电子学报, 2018, 46(12): 2817–2823. doi: 10.3969/j.issn.0372-2112.2018.12.001XIE Anhong, ZHU Lidong, ZHAI Jiqiang, et al. A method of designing covert DSSS-signal for anti-blind detection[J]. Acta Electronica Sinica, 2018, 46(12): 2817–2823. doi: 10.3969/j.issn.0372-2112.2018.12.001 [4] MIRONOV A S, BURDINSKIY I N, and KARABANOV I V. The method of defining the threshold value of the symbolic correlation function for detecting DSSS hydroacoustic signal[C]. International Multi-Conference on Industrial Engineering and Modern Technologies, Vladivostok, Russia, 2018: 1–6. [5] MUNIR M A and MAUD A R M. Direct-sequence spread spectrum with variable spreading sequence for jamming immunity[C]. The 16th International Bhurban Conference on Applied Sciences and Technology, Islamabad, Pakistan, 2019, 933–937. doi: 10.1109/IBCAST.2019.8667119. [6] BOUDER C, AZOU S, and BUREL G. Performance analysis of a spreading sequence estimator for spread spectrum transmissions[J]. Journal of the Franklin Institute, 2004, 341(7): 595–614. doi: 10.1016/j.jfranklin.2004.07.006 [7] QIU Zhaoyang, PENG Hua, and LI Tianyun. A blind despreading and demodulation method for QPSK-DSSS signal with unknown carrier offset based on matrix subspace analysis[J]. IEEE Access, 2019, 7: 125700–125710. doi: 10.1109/ACCESS.2019.2938785 [8] DOMINIQUE F and REED J H. Subspace based PN code sequence estimation for direct sequence signals using a simplified Hebb rule[J]. Electronics Letters, 1997, 33(13): 1119–1120. doi: 10.1049/el:19970778 [9] BOUDER C and BUREL G. Spread spectrum codes identification by neural networks[C]. The 4th World Multiconference on Circuits, Systems, Communications & Computers (CSCC 2000), Vougliameni, Greece, 2000: 257–262. [10] 张天骐, 杨强, 宋玉龙, 等. 一种K-means改进算法的软扩频信号伪码序列盲估计[J]. 电子与信息学报, 2018, 40(1): 226–234. doi: 10.11999/JEIT170306ZHANG Tianqi, YANG Qiang, SONG Yulong, et al. Blind estimation PN sequence in soft spread spectrum signal of improved K-means algorithm[J]. Journal of Electronics &Information Technology, 2018, 40(1): 226–234. doi: 10.11999/JEIT170306 [11] 李军伟, 张天骐, 朱洪波, 等. 基于聚类的多进制扩频伪码序列盲估计方法[J]. 科学技术与工程, 2014, 14(2): 32–36. doi: 10.3969/j.issn.1671-1815.2014.02.008LI Junwei, ZHANG Tianqi, ZHU Hongbo, et al. Clustering based blind estimation of PN sequences in Mary spread spectrum system[J]. Science Technology and Engineering, 2014, 14(2): 32–36. doi: 10.3969/j.issn.1671-1815.2014.02.008 [12] QUI P Y, HUANG Z T, JIANG W L, et al. Improved blind-spreading sequence estimation algorithm for direct sequence spread spectrum signals[J]. IET Signal Processing, 2008, 2(2): 139–146. doi: 10.1049/iet-spr:20070086 [13] DONG Zhanqi and HU Nianying. A method for the detection of long pseudo-random code DSSS signals based on the processing of delay-multiply (II)- The estimation of the information symbol period and the pseudo-random code sequence[C]. The 11th IEEE International Conference on Communication Technology (ICCT), Hangzhou, China, 2008: 233–236. doi: 10.1109/ICCT.2008.4716213. [14] 强幸子. 基于特征提取和最小二乘的直扩信号盲估计[D]. [硕士论文], 重庆邮电大学, 2017: 40–49.QIANG Xingzi. Blind estimation of DSSS signals based on feature extraction and least square[D]. [Master dissertation], Chongqing University of Posts and Telecommunications, 2017: 40–49. [15] 何涛, 李志强, 梁旭文. 一种非周期调制直扩信号扩频码估计方法[J]. 宇航学报, 2013, 34(4): 546–551. doi: 10.3873/j.issn.1000-1328.2013.04.014HE Tao, LI Zhiqiang, and LIANG Xuwen. An estimation method for spread spectrum code of non-periodic modulated DS signal[J]. Journal of Astronautics, 2013, 34(4): 546–551. doi: 10.3873/j.issn.1000-1328.2013.04.014 [16] 周杨, 张天骐. 同/异步短码DS-CDMA信号伪码序列及信息序列盲估计[J]. 电子与信息学报, 2019, 41(7): 1540–1547. doi: 10.11999/JEIT180812ZHOU Yang and ZHANG Tianqi. Blind estimation of the pseudo noise sequence and information sequence for short code synchronous and asynchronous DS-CDMA signal[J]. Journal of Electronics &Information Technology, 2019, 41(7): 1540–1547. doi: 10.11999/JEIT180812 [17] KAY S M, 罗鹏飞, 译. 统计信号处理基础[M]. 北京: 电子工业出版社, 2014: 29–33.KAY S M, LUO Pengfei, translation. Fundamentals of Statistical Signal Processing[M]. Beijing: Publishing House of Electronics Industry, 2014: 29–33. [18] 张天骐, 张传武, 林孝康, 等. 直扩信号伪码周期及序列的估计算法[J]. 系统工程与电子技术, 2005, 27(8): 1365–1368. doi: 10.3321/j.issn:1001-506X.2005.08.011ZHANG Tianqi, ZHANG Chuanwu, LIN Xiaokang, et al. Algorithms for period and sequence estimation of the PN code in DS-SS signals[J]. Systems Engineering and Electronics, 2005, 27(8): 1365–1368. doi: 10.3321/j.issn:1001-506X.2005.08.011 [19] 徐海源, 王丰华, 黄知涛, 等. 长码直扩信号的符号速率盲估计方法[J]. 国防科技大学学报, 2007, 29(6): 44–48. doi: 10.3969/j.issn.1001-2486.2007.06.011XU Haiyuan, WANG Fenghua, HUANG Zhitao, et al. Blind estimation of the symbol rate of a long code DSSS signal[J]. Journal of National University of Defense Technology, 2007, 29(6): 44–48. doi: 10.3969/j.issn.1001-2486.2007.06.011 [20] BOUDER C, AZOU S, and BUREL G. A robust synchronization procedure for blind estimation of the symbol period and the timing offset in spread spectrum transmissions[C]. IEEE Seventh International Symposium on Spread Spectrum Techniques and Applications, Prague, Czech Republic, 2002: 238–241. doi: 10.1109/ISSSTA.2002.1049322. [21] STOICA P and NG B C. On the Cramer-Rao bound under parametric constraints[J]. IEEE Signal Processing Letters, 1998, 5(7): 177–179. doi: 10.1109/97.700921 -








 下载:
下载:





 下载:
下载:
