A Fast Direction Estimation Algorithm Based on Vector Hydrophone Array under Non-ideal Conditions
-
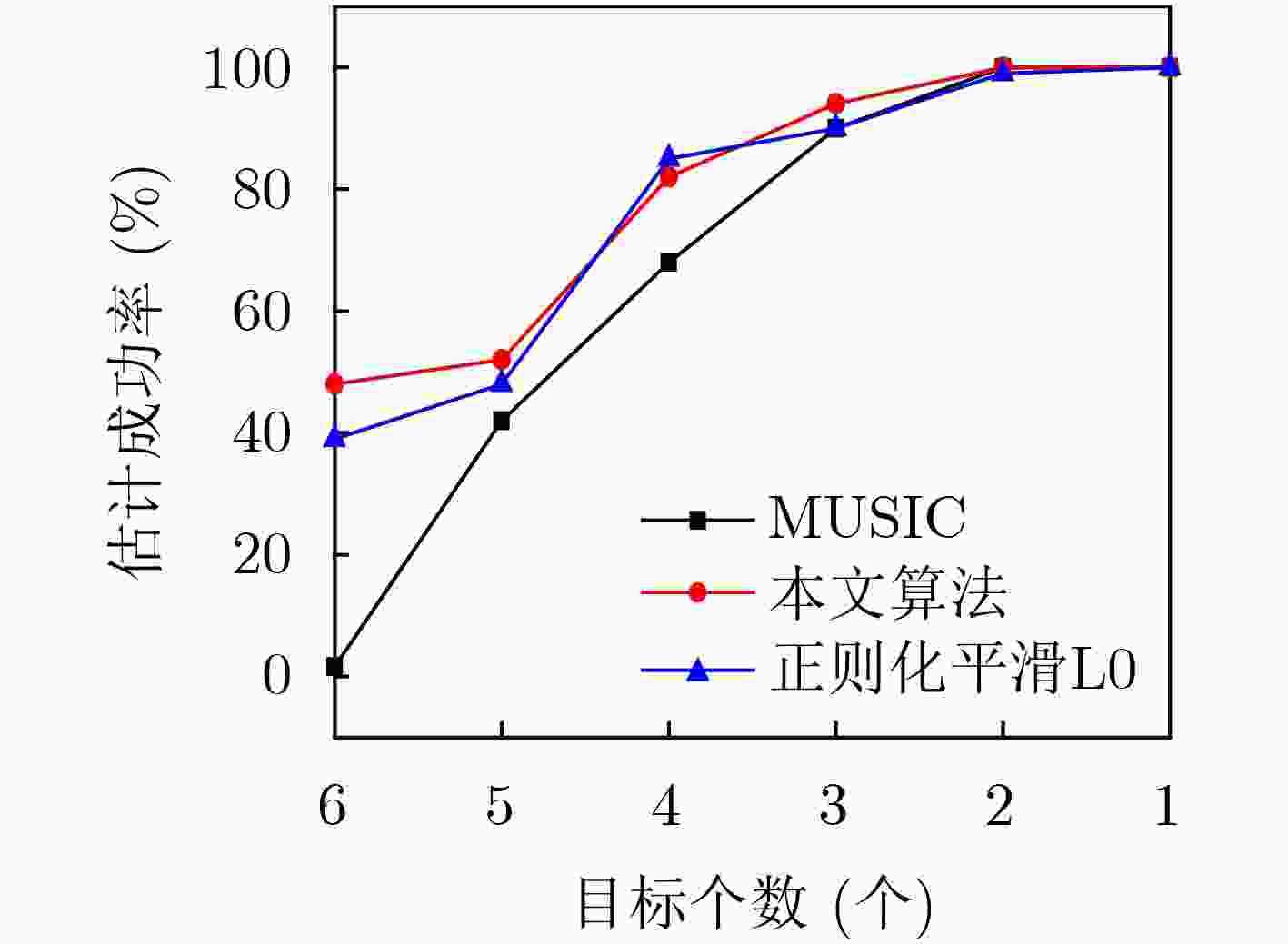
摘要: 为了实现少快拍、低信噪比(SNR)条件下的水下目标快速方位估计,该文建立矢量水听器阵列方位估计稀疏表示模型。利用实值转化技术将复数方向矩阵转化到实数域,以便利用平滑L0算法对稀疏信号矩阵进行重构从而得到方位估计结果。该文改进平滑L0算法,利用收敛性更好的复合反比例函数(CIPF)函数作为平滑函数以及提出促稀疏加权的方法,该方法通过加权的方式修正噪声条件下L2范数作为迭代初始值偏离稀疏解较远的问题来促进算法快速收敛于稀疏解。通过仿真验证了该文提出的基于实值转换的促稀疏加权平滑L0算法在少快拍、低信噪比的条件下可以实现优于传统子空间类算法的性能,并且在保证性能的同时,显著提高方位估计的速度。Abstract: In order to realize the fast direction estimation of underwater targets under the conditions of less snapshot and low SNR, a sparse decomposition model of vector hydrophone array direction estimation is established. The real value conversion technique is used to convert the complex direction matrix into the real number field, so as to reconstruct the sparse signal matrix using the SL0 algorithm to obtain the orientation estimation result. The SL0 algorithm is improved, the Compound Inverse Proportional Function (CIPF) with better convergence is used as a smoothing function, and a weighted method is proposed which can promote sparsity, the weighted method is used to correct the problem that the norm as the initial iteration value deviates far from the sparse solution to increase the speed of azimuth estimation. The simulation verifies that the proposed algorithm can achieve better performance than the traditional subspace algorithm under the conditions of low snapshot and low SNR, and improve the speed of bearing estimation while ensuring performance.
-
Key words:
- Vector hydrophone /
- DOA estimate /
- Sparse decomposition
-
表 1 基于实值转换的促稀疏加权平滑L0算法步骤
(1) 进行L次快拍采样,得到矢量阵列输出${{X}}$; (2) 建立过完备原子库${{A}}\left( {{\tilde{{ \theta }}}} \right)$,利用实值变换酉矩阵将定义在复数域的${{A}}\left( {{\tilde{{ \theta }}}} \right)$转换成实数矩阵${\overline {{A}} _{{\rm{RV}}}}\left( {{\tilde{{ \theta }}}} \right)$ 并且通过分离实部与虚部,获得扩
展的2L次快拍的${{{X}}_{{\rm{RV}}}}$;(3) 按照如下步骤进行基于实值转换的促稀疏加权平滑L0算法从而实现矢量阵列DOA估计: 初始化:设置权重${W^0}$为全1向量;令${{\tilde{{ S}}}_{{\rm{RV}}}}^0$为最小L2范数解。 ——For k=1: 2L; (a) 当$k \ge 2$时,令${W^k}{\rm{ = }}{W^{k - 1}} - \lambda \left( {{W^{k - 1}} - {{{\tilde{{ S}}}}_{{\rm{RV}}}}{^{ k- 1}}} \right)$,则${ {\tilde{{ S} } }_{ {\rm{RV} } } }^{\rm{k} }{\rm{ = } }{ {{W} }^k}{ {\tilde{{ S} } }_{ {\rm{RV} } } }{^{ {{k} }{ - 1} } }$,选择一组下降的${{\sigma }}{\rm{ = }}\left[ {\begin{array}{*{20}{c}} {{\sigma _1}}&{{\sigma _2}}& ··· &{{\sigma _n}} \end{array}} \right]$,
其中${\sigma _1}{\rm{ = }}4{\rm{max}}\left| {{{{\tilde{{ S}}}}_{{\rm{RV}}}}^k} \right|$, ${\sigma _i}{\rm{ = 0}}{\rm{.6}}{\sigma _{i - 1}}$;——For i=1: N。 (b)令$ \sigma = {\sigma _i}$; (c)通过最速下降法进行迭代,通过以下步骤循环迭代H次,找到平滑函数的最值。 ① 设置$ {{\tilde{{ S}}}_{{\rm{RV}}}}^k{\rm{ = }}{{\tilde{{ S}}}^k}_{{\rm{RV}}}$; ② For h=1:H;
(i) 计算$ \Delta {{\tilde{{ S}}}^k}_{{\rm{RV}}}{\rm{ = }}\left[ {\begin{array}{*{20}{c}} {\dfrac{{20{\sigma _i}{{{\tilde{{ S}}}}^k}_{{\rm{RV}}1}}}{{{{\left[ {10{{\left( {{{{\tilde{{ S}}}}^k}{{_{{\rm{RV}}1}}^k}} \right)}^2} + {\sigma _{\rm{i}}}^2} \right]}^2}}}}&{\dfrac{{20{\sigma _i}{{{\tilde{{ S}}}}^k}_{{\rm{RV}}2}}}{{{{\left[ {10{{\left( {{{{\tilde{{ S}}}}^k}{{_{{\rm{RV}}2}}^k}} \right)}^2} + {\sigma _i}^2} \right]}^2}}}}& ··· &{\dfrac{{20{\sigma _h}{{{\tilde{{ S}}}}_{{\rm{RV}}P}}}}{{{{\left[ {10{{\left( {{{{\tilde{{ S}}}}_{{\rm{RV}}P}}^k} \right)}^2} + {\sigma _h}^2} \right]}^2}}}} \end{array}} \right]$;(ii)计算$ {{\tilde{{ S}}}^k}_{{\rm{RV}}} \leftarrow {{\tilde{{ S}}}^k}_{{\rm{RV}}} - \Delta {{\tilde{{ S}}}^k}_{{\rm{RV}}}$; (iii)将${{\tilde{{ S}}}^{\rm{k}}}_{{\rm{RV}}}$投影到可行域,即${{\tilde{{ S}}}^k}_{{\rm{RV}}} \leftarrow {{\tilde{{ S}}}^k}_{{\rm{RV}}} - {\overline {{A}} ^{\rm{T}}}{\left( {\overline {{A}} {{\overline {{A}} }^{\rm{T}}} + {\lambda ^{ - 1}}{{{I}}_n}} \right)^{ - 1}}\left( {\overline {{A}} {{{\tilde{{ S}}}}^k}_{{\rm{RV}}} - {{{X}}_{{\rm{RV}}}}} \right)$。 End ③ 设置$ {{\tilde{{ S}}}^k}_{{\rm{RV}}\left( i \right)}{\rm{ = }}{{\tilde{{ S}}}^k}_{{\rm{RV}}}$。 End 本次快拍的方位估计结果为${{\tilde{{ S}}}^k}_{{\rm{RV}}}{\rm{ = }}{{\tilde{{ S}}}^k}_{{\rm{RV}}\left( N \right)}$。 ——End (4) 处理完2L快拍数据后,最终可得到方位估计结果。 表 2 不同算法运行时间比较
算法名称 平滑函数 运行时间(s) 平滑L0 Gauss 0.4311 正则化平滑L0 Gauss 0.4560 本文算法 Gauss 0.2967 本文算法 CIPF 0.2501 -
杨德森, 朱中锐, 田迎泽. 矢量声呐技术理论基础及应用发展趋势[J]. 水下无人系统学报, 2018, 26(3): 185–192. doi: 10.11993/j.issn.2096-3920.2018.03.001YANG Desen, ZHU Zhongrui, and TIAN Yingze. Theoretical bases and application development trend of vector sonar technology[J]. Journal of Unmanned Undersea Systems, 2018, 26(3): 185–192. doi: 10.11993/j.issn.2096-3920.2018.03.001 SCHMIDT R. Multiple emitter location and signal parameter estimation[J]. IEEE Transactions on Antennas and Propagation, 1986, 34(3): 276–280. doi: 10.1109/TAP.1986.1143830 柳艾飞, 杨德森, 时胜国, 等. 各向同性噪声场中单矢量传感器虚源消除MUSIC测向方法[J]. 声学学报, 2019, 44(4): 698–706. doi: 10.15949/j.cnki.0371-0025.2019.04.030LIU Aifei, YANG Desen, SHI Shengguo, et al. MUSIC direction of arrival estimation method with virtual source elimination for single vector sensor under isotropic ambient noise background[J]. Acta Acustica, 2019, 44(4): 698–706. doi: 10.15949/j.cnki.0371-0025.2019.04.030 王钢, 周若飞, 邹昳琨. 基于压缩感知理论的图像优化技术[J]. 电子与信息学报, 2020, 42(1): 222–233. doi: 10.11999/JEIT190669WANG Gang, ZHOU Ruofei, and ZOU Yikun. Research on image optimization technology based on compressed sensing[J]. Journal of Electronics &Information Technology, 2020, 42(1): 222–233. doi: 10.11999/JEIT190669 HE Zhenqing, SHI Zhiping, and HUANG Lei. Covariance sparsity-aware DOA estimation for nonuniform noise[J]. Digital Signal Processing, 2014, 28: 75–81. doi: 10.1016/j.dsp.2014.02.013 蒋莹, 王冰切, 韩俊, 等. 基于分布式压缩感知的宽带欠定信号DOA估计[J]. 电子与信息学报, 2019, 41(7): 1690–1697. doi: 10.11999/JEIT180723JIANG Ying, WANG Bingqie, HAN Jun, et al. Underdetermined wideband DOA estimation based on distributed compressive sensing[J]. Journal of Electronics &Information Technology, 2019, 41(7): 1690–1697. doi: 10.11999/JEIT180723 BU Hongxia, TAO Ran, BAI Xia, et al. Regularized smoothed ℓ0 norm algorithm and its application to CS-based radar imaging[J]. Signal Processing, 2016, 122: 115–122. doi: 10.1016/j.sigpro.2015.11.024 WANG Linyu, YIN Xiangjun, YUE Huihui, et al. A regularized weighted smoothed L0 norm minimization method for underdetermined blind source separation[J]. Sensors, 2018, 18(12): 4260. doi: 10.3390/s18124260 张小飞, 汪飞, 徐大专. 阵列信号处理的理论和应用[M]. 北京: 国防工业出版社, 2010: 45–80.ZHANG Xiaofei, WANG Fei, and XU Dazhuan. Theory and Application of Array Signal Processing[M]. Beijing: National Defense Industry Press, 2010: 45–80. 王峰, 向新, 易克初, 等. L0范数平滑逼近的稳健求解算法[J]. 电子与信息学报, 2015, 37(10): 2377–2382. doi: 10.11999/JEIT141590WANG Feng, XIANG Xin, YI Kechu, et al. Robust computational methods for smoothed L0 approximation[J]. Journal of Electronics &Information Technology, 2015, 37(10): 2377–2382. doi: 10.11999/JEIT141590 ZHANG Chunjie, HAO Dongbin, HOU Changbo, et al. A new approach for sparse signal recovery in compressed sensing based on minimizing composite trigonometric function[J]. IEEE Access, 2018, 6: 44894–44904. doi: 10.1109/ACCESS.2018.2855958 DAI Jisheng, XU Xin, and ZHAO Dean. Direction-of-arrival estimation via real-valued sparse representation[J]. IEEE Antennas and Wireless Propagation Letters, 2013, 12: 376–379. doi: 10.1109/LAWP.2013.2252415 刘婧. 非理想条件下DOA估计算法研究[D]. [博士论文], 哈尔滨工程大学, 2018: 16–17.LIU Jing. Research on DOA estimation algorithm for non-ideal conditions[D]. [Ph. D. dissertation], Harbin Engineering University, 2018: 16–17. -





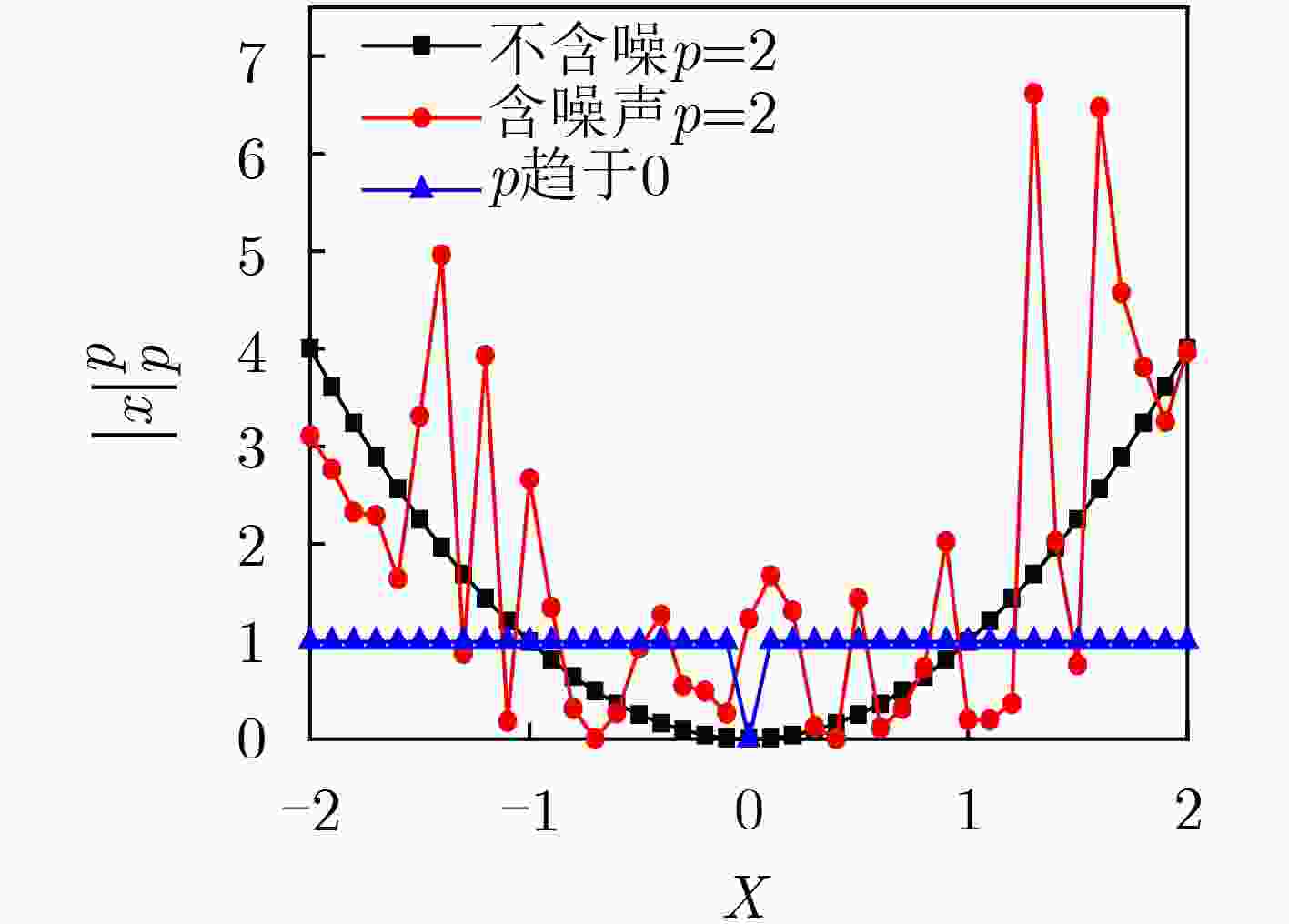


 下载:
下载:
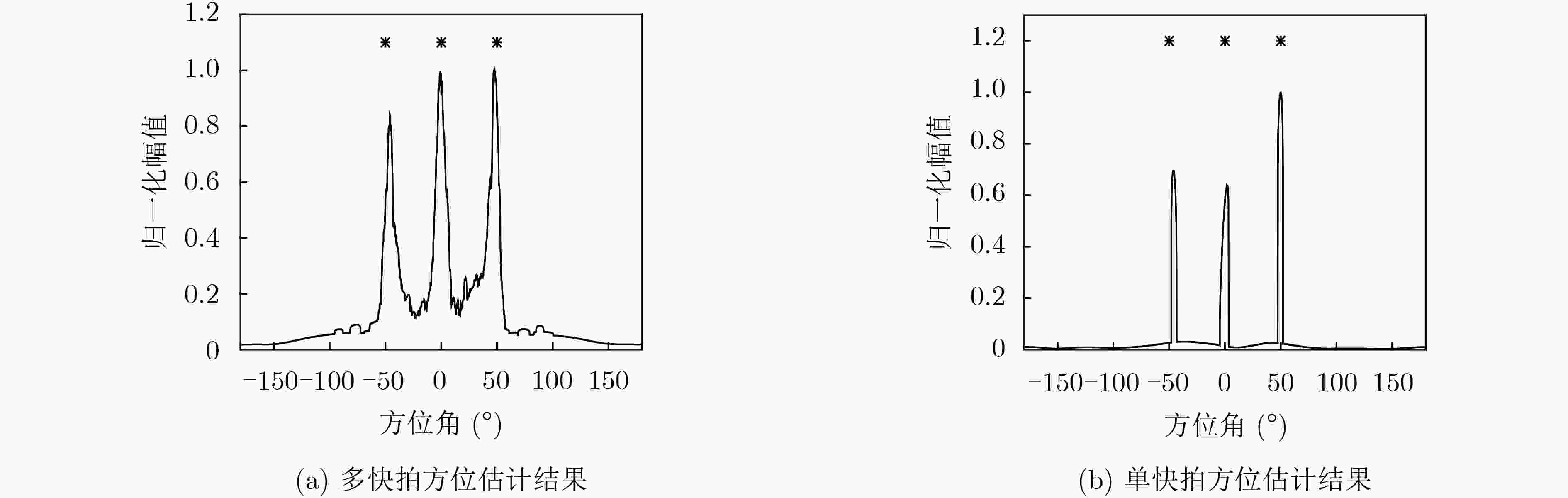
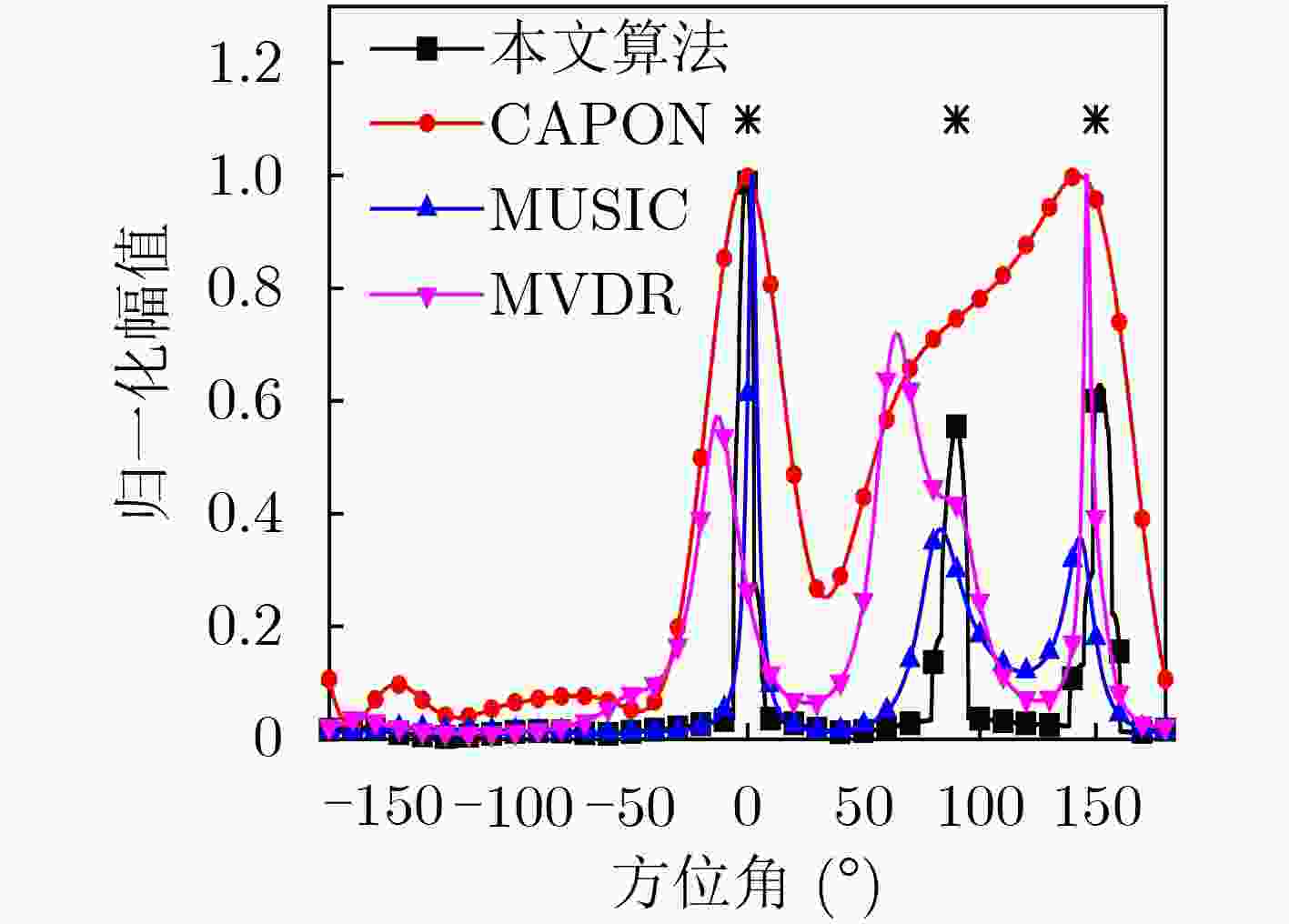
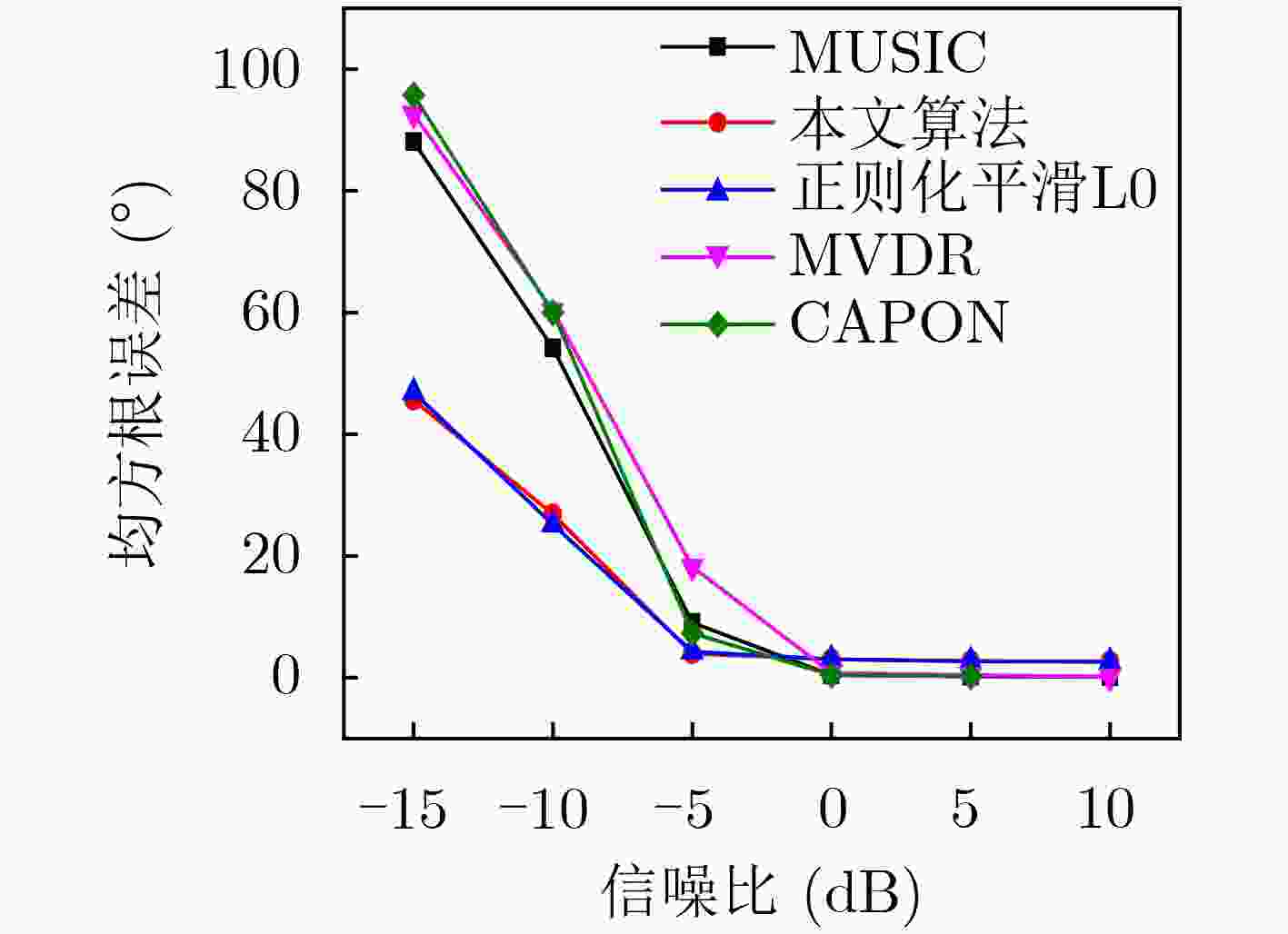


 下载:
下载:
