基于Ransac算法的捷变频联合正交频分复用雷达高速多目标参数估计

全英汇; 高霞; 沙明辉; 方文; 李亚超; 邢孟道

doi:10.11999/JEIT200529

基于Ransac算法的捷变频联合正交频分复用雷达高速多目标参数估计

doi: 10.11999/JEIT200529

1.
西安电子科技大学电子工程学院西安 710071
2.
北京无线电测量研究所北京 100854
3.
西安电子科技大学雷达信号处理国家重点实验室西安 710071

基金项目: 国家自然科学基金(61303035, 61772397)，中央高校基本科研业务费专项资金，西安电子科技大学研究生创新基金

详细信息

作者简介:
全英汇：男，1981年生，博士，教授，研究方向为雷达信号处理、主动波形对抗

高霞：女，1996年生，硕士生，研究方向为雷达信号处理

沙明辉：男，1986年生，博士生，研究方向为雷达抗干扰和信号处理

方文：男，1996年生，硕士生，研究方向为雷达信号处理

李亚超：男，1981年生，博士，教授，研究方向为雷达成像和实时信号处理

邢孟道：男，1975年生，博士，教授，研究方向为SAR/ISAR成像、动目标检测等

通讯作者:
高霞　2636897970@qq.com

中图分类号: TN957.51
计量
- 文章访问数: 1108
- HTML全文浏览量: 408
- PDF下载量: 67
- 被引次数: 0
出版历程
- 收稿日期: 2020-06-29
- 修回日期: 2020-12-06
- 网络出版日期: 2020-12-15
- 刊出日期: 2021-07-10

High Speed Multi-target Parameter Estimation for FA-OFDM Radar Based on Ransac Algorithm

1.
School of Electronic Engineering, Xidian University, Xi’an 710071, China
2.
Beijing Institute of Radio Measurement, Beijing 100854, China
3.
National Key Laboratory of Radar Signal Processing, Xidian University, Xi’an 710071, China

Funds: The National Natural Science Foundation of China (61303035, 61772397), The Foundation Research Funds for Central University, The Innovation Fund of Xidian University

摘要

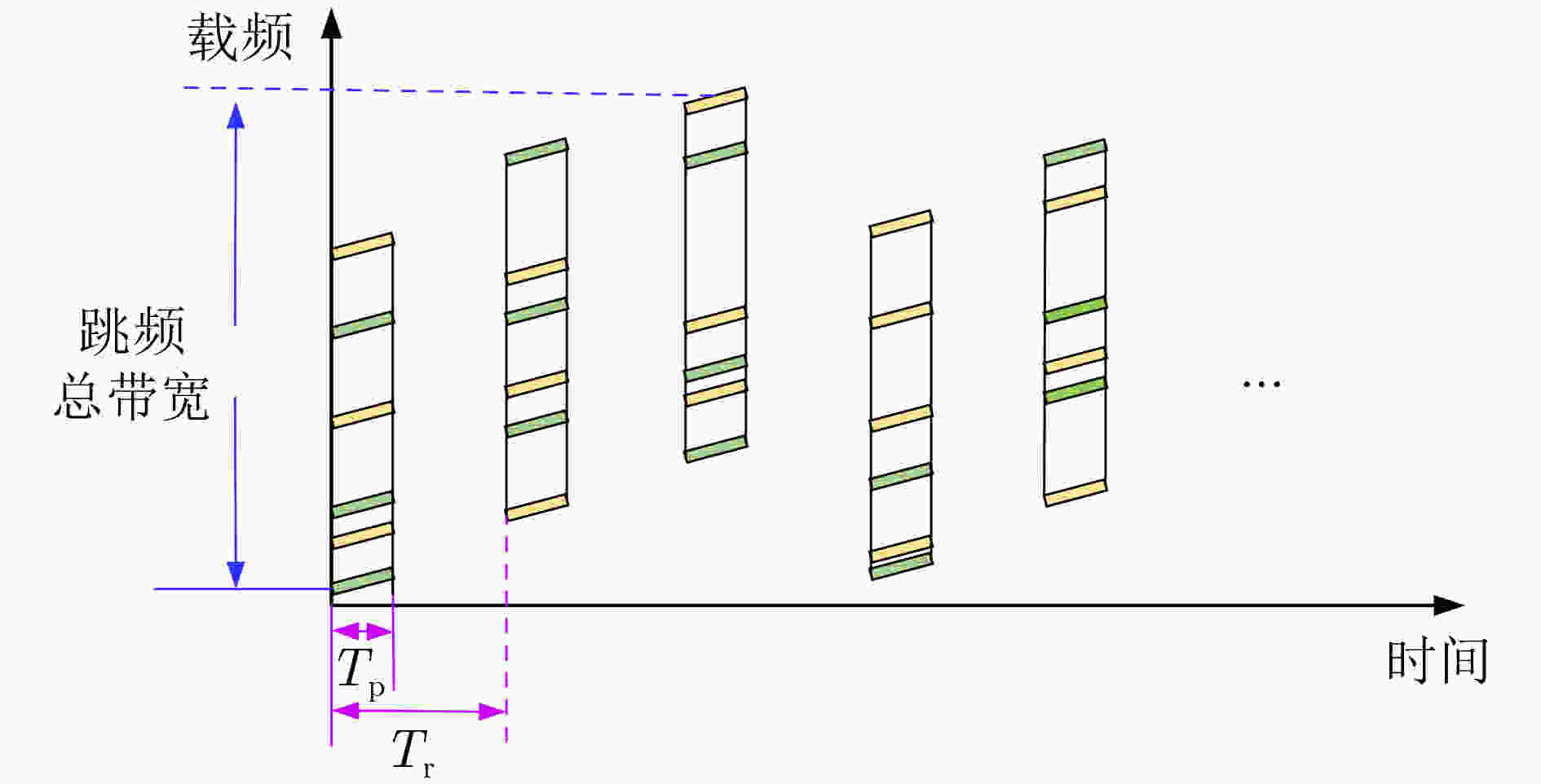
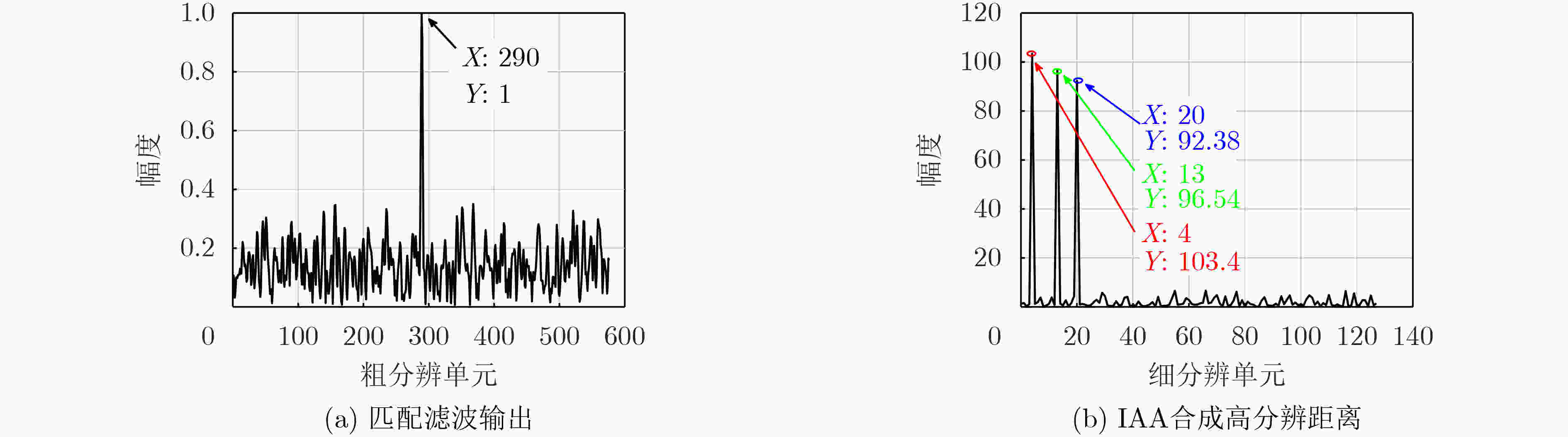
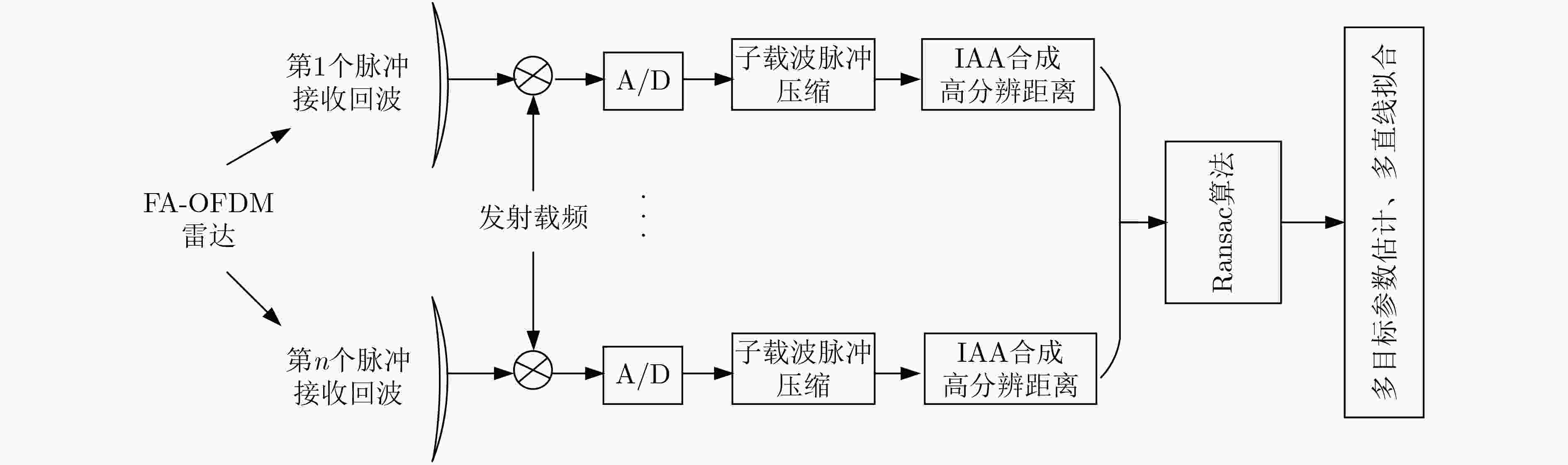
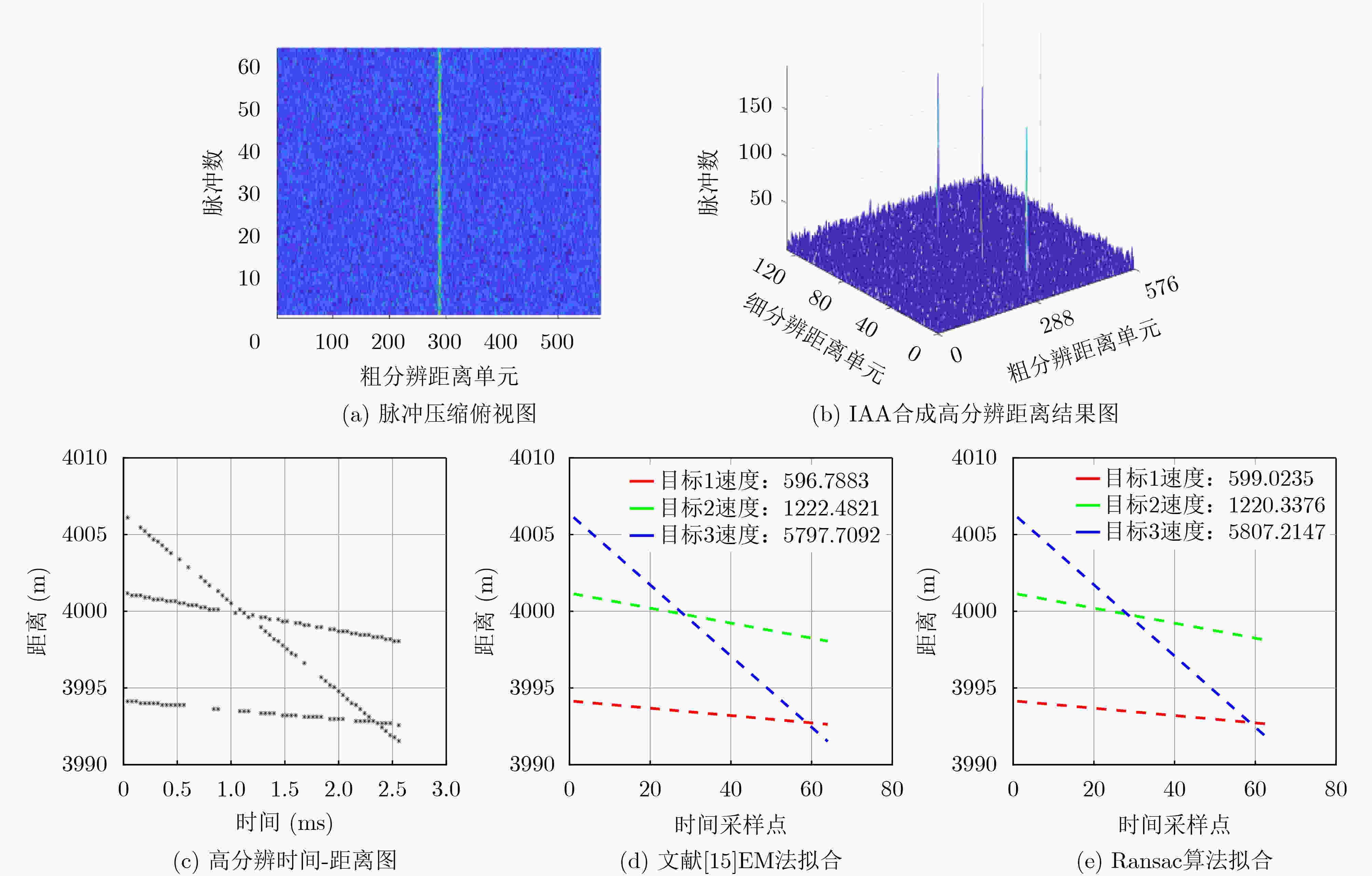
摘要: 在现代雷达电子战场中，目标检测与其参数估计有着非常重要的意义。因此，该文提出了一种基于随机抽样一致算法(Ransac)的捷变频联合正交频分复用(FA-OFDM)雷达高速多目标参数估计的方法。首先，在传统捷变频雷达的每个脉冲内同时发射多个频率随机跳变的窄带OFDM子载波。将单个脉冲内所有子载波的回波信号进行脉冲压缩后，采用迭代自适应谱估计(IAA)算法合成目标的高分辨距离。然后，分别对各个脉冲的回波进行脉冲压缩和迭代自适应谱估计，得到不同脉冲时刻的高分辨距离，构成观测数据集。再根据Ransac算法估计信号参数模型的步骤，拟合多条时间-距离直线，进而对高速运动的多个目标同时进行参数估计。最后，分别分析了信噪比(SNR)对检测概率以及目标自身速度对其相对估计误差的影响。仿真实验验证了所提算法的有效性。
- 参数估计 /
- 高速多目标 /
- 捷变频联合正交频分复用雷达 /
- 迭代自适应谱估计算法 /
- 随机抽样一致算法
Abstract: In modern radar electronic battlefield, target detection and parameter estimation have great significance. Therefore, a high-speed multi-target parameter estimation method for Frequency Agile-Orthogonal Frequency Division Multiplexing (FA-OFDM) radar based on Random sampling consensus (Ransac) algorithm is proposed in this paper. Firstly, multiple narrowband OFDM subcarriers with random frequency hopping are simultaneously transmitted in each pulse of conventional frequency agile radar. The echo signals of all subcarriers in a single pulse are compressed, and then the high-resolution range of the target is synthesized by Iterative Adaptive Approach (IAA) algorithm. Furthermore, the echoes of each pulse are compressed and iterative adaptive spectrum estimated, and the high-resolution distance of different pulse time is obtained to form the observation data set. Then, according to the steps of the Ransac algorithm to estimate the signal parameter model, multiple time-distance lines are fitted, and then parameters of multiple high-speed moving targets are estimated at the same time. Finally, the influence of the Signal-to-Noise Ratio (SNR) on detection probability and the target velocity on relative error of estimation are analyzed, respectively. Simulations are provided to verify the effectiveness of the proposal.

HTML全文

图 1 FA-OFDM雷达发射信号示意图

下载: 全尺寸图片幻灯片

图 2 3个相邻目标仿真结果图

下载: 全尺寸图片幻灯片

图 3 基于Ransac算法的高速多目标参数估计方法的流程图

下载: 全尺寸图片幻灯片

图 4 信噪比为–12 dB时的仿真结果

下载: 全尺寸图片幻灯片

图 5 信噪比为–28 dB时的仿真结果

下载: 全尺寸图片幻灯片

图 6 信噪比对检测概率的影响

下载: 全尺寸图片幻灯片

图 7 目标速度对估计误差的影响

下载: 全尺寸图片幻灯片

图 8 输出SNR对RMSE的影响

下载: 全尺寸图片幻灯片

表 1 仿真参数

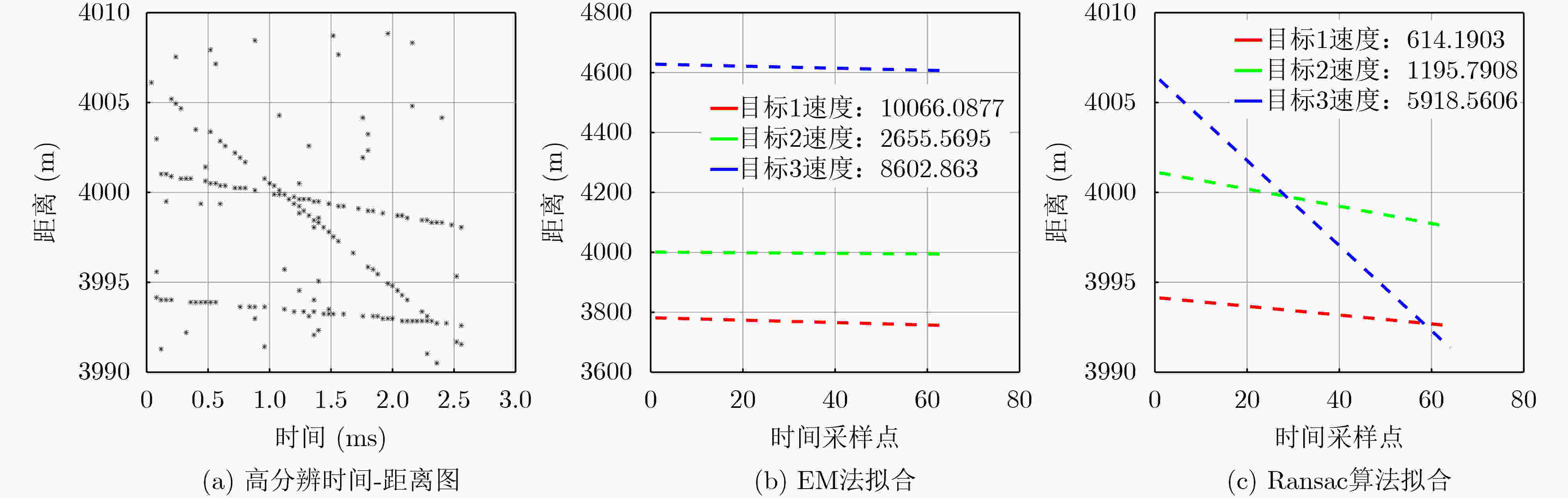
参数	数值	参数	数值
脉冲宽度	4 μs	脉冲重复频率	25 kHz
信号带宽	24 MHz	采样频率	48 MHz
子载波个数	64	中心载频	14 GHz
跳频总数	128	跳频带宽	20 MHz
脉冲总数	64	输入信噪比	–12 dB / –28 dB
目标距离	[3994, 4001, 4006] m	目标速度	[600, 1220, 5800] m/s

下载: 导出CSV

参考文献(21)

[1]	JANKIRAMAN M, WESSELS B J, and VAN GENDEREN P. Design of a multifrequency FMCW radar[C]. The 28th European Microwave Conference, Amsterdam, Netherlands, 1998: 548–589. doi: 10.1109/EUMA.1998.338053.
[2]	JANKIRAMAN M, WESSELS B J, and VAN GENDEREN P. Pandora multifrequency FMCW/SFCW radar[C].IEEE National Radar Conference, Alexandria, USA, 2000: 750–757. doi: 10.1109/RADAR.2000.851929.
[3]	霍凯, 赵晶晶. OFDM新体制雷达研究现状与发展趋势[J]. 电子与信息学报, 2015, 37(11): 2776–2785. doi: 10.11999/JEIT150335 HUO Kai and ZHAO Jingjing. The Development and prospect of the new OFDM radar[J]. Jounal of Electronics &Information Technology, 2015, 37(11): 2776–2785. doi: 10.11999/JEIT150335
[4]	WANG Jun, ZHANG Bochen, and LEI Peng. Ambiguity function analysis for OFDM radar signals[C]. CIE International Conference on Radar, Guangzhou, China, 2016: 10-13. doi: 10.1109/RADAR.2016.8059592.
[5]	肖博, 霍凯, 刘永祥. 雷达通信一体化研究现状与发展趋势[J]. 电子与信息学报, 2019, 41(3): 739–749. doi: 10.11999/JEIT180515 XIAO Bo, HUO Kai, and LIU Yongxiang. Development and Prospect of Radar and Communication Integration[J]. Jounal of Electronics &Information Technology, 2019, 41(3): 739–749. doi: 10.11999/JEIT180515
[6]	刘冰凡, 陈伯孝. 基于OFDM-LFM信号的MIMO雷达通信一体化信号共享设计研究[J]. 电子与信息学报, 2019, 41(4): 801–808. doi: 10.11999/JEIT180547 LIU Bingfan and CHEN Baixiao. Integration of MIMO Radar and Communication with OFDM-LFM Signals[J]. Jounal of Electronics &Information Technology, 2019, 41(4): 801–808. doi: 10.11999/JEIT180547
[7]	SCHWEIZER B, SCHINDLER D, KNILL C, et al. Expanding the unambiguous velocity limitation of the stepped-carrier OFDM radar scheme[C]. The 15th European Radar Conference, Madrid, Spanish, 2018: 26–28. doi: 10.23919/EuRAD.2018.8546621.
[8]	SCHWEIZER B, KNILL C, SCHINDLER D et al. Stepped-Carrier OFDM-Radar processing scheme to retrieve high-resolution range-velocity profile at low sampling rate[J]. IEEE Transactions on Microwave Theory and Techniques, 2018, 66(3): 1610–1618. doi: 10.1109/TMTT.2017.2751463
[9]	LELLOUCH G, TRAN P, PRIBIC R, et al. OFDM waveforms for frequency agility and opportunities for Doppler processing in radar[C]. IEEE Radar Conference, Rome, Italy, 2008: 1–6. doi: 10.1109/RADAR.2008.4720798.
[10]	HUO Kai, DENG B, LIU Y, et al. The principle of synthesizing HRRP based on a new OFDM phase-coded stepped-frequency radar signal[C]. IEEE 10th International Conference On Signal Processing Proceedings, Beijing, China, 2010: 1994–1998. doi: 10.1109/ICOSP.2010.5655889.
[11]	LELLOUCH G, PRIBIC R and VAN GENDEREN P. Frequency agile stepped OFDM waveform for HRR[C]. 2009 International Waveform Diversity and Design Conference, Kissimmee, USA, 2009: 90–93. doi: 10.1109/WDDC.2009.4800321.
[12]	黄瑞, 杜小勇, 胡卫东. OFDM雷达多目标运动参数的近似最大似然估计[J]. 雷达学报, 2018, 7(4): 507–513. doi: 10.12000/JR17116 HUANG Rui, DU Xiaoyong and HU Weidong. Approximate maximum likelihood estimator of multi-target motion parameters for orthogonal frequency division multiplexing radar[J]. Journal Of Radars, 2018, 7(4): 507–513. doi: 10.12000/JR17116
[13]	全英汇, 高霞, 沙明辉, 等. 基于期望最大化算法的捷变频联合正交频分复用雷达高速多目标参数估计[J]. 电子与信息学报, 2018, 7(4): 507–513. doi: 10.11999/JEIT190474 QUAN Yinghui, GAO Xia, SHA Minghui, et al. High Speed Multi-target Parameter Estimation for FA-OFDM Radar Based on Expectation Maximization Algorithm[J]. Jounal of Electronics &Information Technology, 2018, 7(4): 507–513. doi: 10.11999/JEIT190474
[14]	QUAN Yinghui, LI Yachao, WU Yaojun, et al. Moving target detection for frequency agility radar by sparse reconstruction[J]. Rev. Sci. Instrum., 2016, 87(9): 811–815. doi: 10.1049/el.2011.1293
[15]	QUAN Yinghui, WU Yaojun, LI Yachao, et al. Range–Doppler reconstruction for frequency agile and PRF-jittering radar[J]. IET Radar, Sonar & Navigation, 2018, 12(3): 348–352. doi: 10.1049/iet-rsn.2017.0421
[16]	章平亮. 自适应迭代谱估计的统一分析与拓展[D]. 复旦大学. 2013: 9–20. ZHANG Pingliang. Unified analysis and development of adaptive iterative spectrum estimation[D]. Fudan University. 2013: 9–20.
[17]	JENSEN J R, GLENTIS G O, CHRISTENSEN M G, et al. Computationally efficient IAA-based estimation of the fundamental frequency[C]. 2012 Proceedings of the 20th European Signal Processing Conference(EUSIPCO), Bucharest, Romania, 2012.
[18]	GLENTIS G O and JAKOBSSON A. Efficient implementation of iterative adaptive approach spectral estimation techniques[J]. IEEE Transactions on Signal Processing, 2011, 59(7): 4154–4167. doi: 10.1109/TSP.2011.2145376
[19]	XUE Ming, XU Luzhou, and LI Jian. IAA Spectral Estimation: Fast implementation using the Gohberg-Semencul factorization[J]. IEEE Transactions on Signal Processing, 2011, 59(7): 3251–3261. doi: 10.1109/ICASSP.2011.5947305
[20]	ZHAO Mingfu, CHEN Haijun, SONG Tao, et al. Research on image matching based on improved RANSAC-SIFT algorithm[C]. 2017 16th International Conference on Optical Communications and Networks (ICOCN), Wuzhen, China, 2017: 1–3. doi: 10.1109/ICOCN.2017.8121270.
[21]	RAZA M A, AWAIS REHMAN M, QURESHI I M, et al. Mahmood. A Simplified approach to Visual Odometry using Graph Cut RANSAC[C]. 2018 5th International Multi-Topic ICT Conference (IMTIC), Jamshoro, 2018: 1–7. doi: 10.1109/IMTIC.2018.8467263.