一种多维信源衰减延时混合的欠定盲源分离方法

马宝泽; 张天骐; 安泽亮; 张刚

doi:10.11999/JEIT200524

一种多维信源衰减延时混合的欠定盲源分离方法

doi: 10.11999/JEIT200524

重庆邮电大学通信与信息工程学院重庆 400065

基金项目: 国家自然科学基金(61671095，61371164)

详细信息

作者简介:
马宝泽：男，1990年生，博士生，研究方向为盲信号分离及深度学习

张天骐：男，1971年生，教授，博士后，研究方向为扩频信号的盲处理、神经网络实现以及信号的同步处理

安泽亮：男，1993年生，博士生，研究方向为深度学习在扩频通信中的应用

张刚：男，1976年生，教授，博士，研究方向为微弱信号检测和混沌保密通信

通讯作者:
马宝泽　d170101009@stu.cqupt.edu.cn

中图分类号: TN911.7
计量
- 文章访问数: 949
- HTML全文浏览量: 384
- PDF下载量: 70
- 被引次数: 0
出版历程
- 收稿日期: 2020-06-29
- 修回日期: 2021-02-21
- 网络出版日期: 2021-03-31
- 刊出日期: 2021-08-10

An Underdetermined Blind Source Separation Approach for Attenuated and Time-delayed Mixtures of Multiple Sources

School of Communication and Information Engineering, Chongqing University of Posts and Telecommunications, Chongqing 400065, China

Funds: The National Natural Science Foundation of China (61671095, 61371164)

摘要

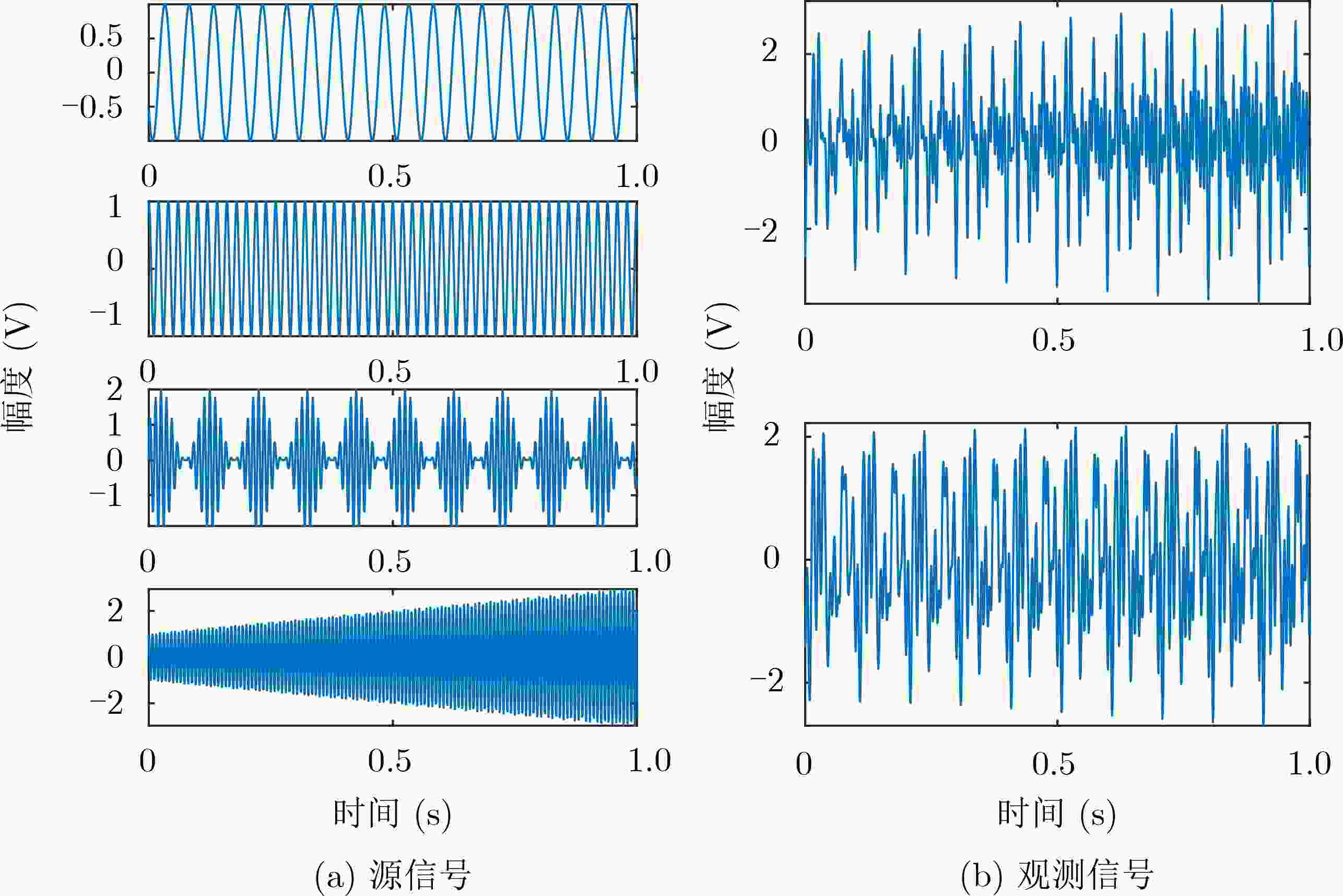
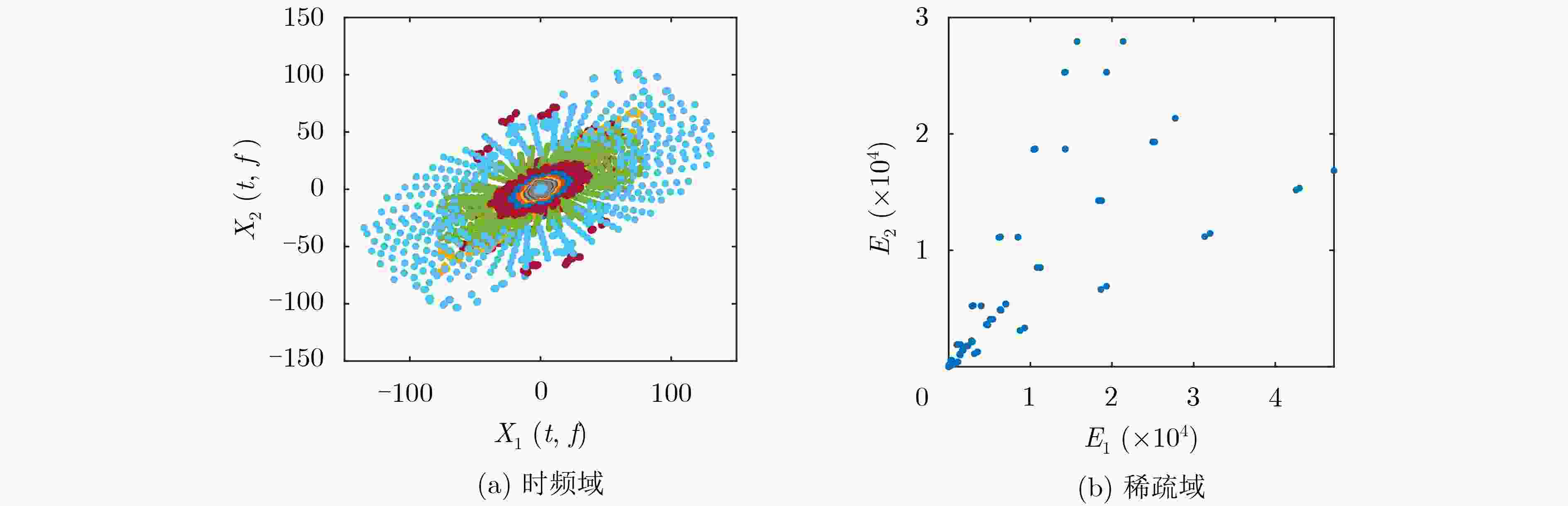
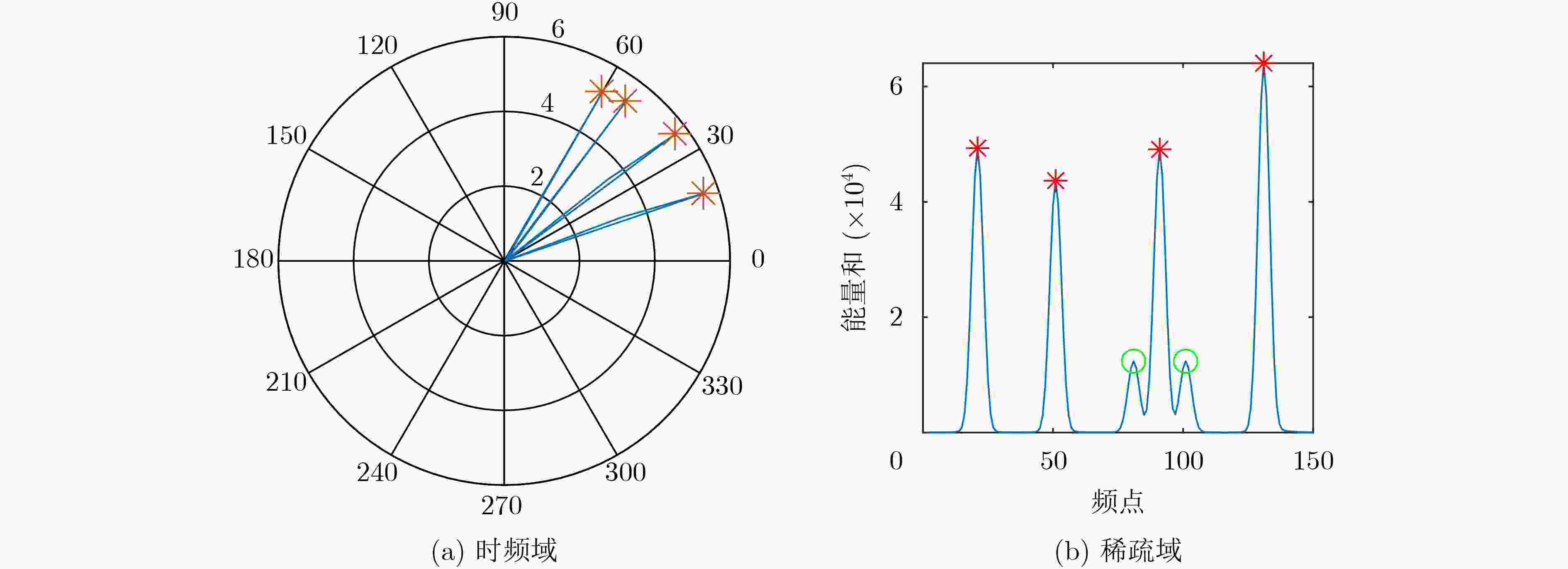
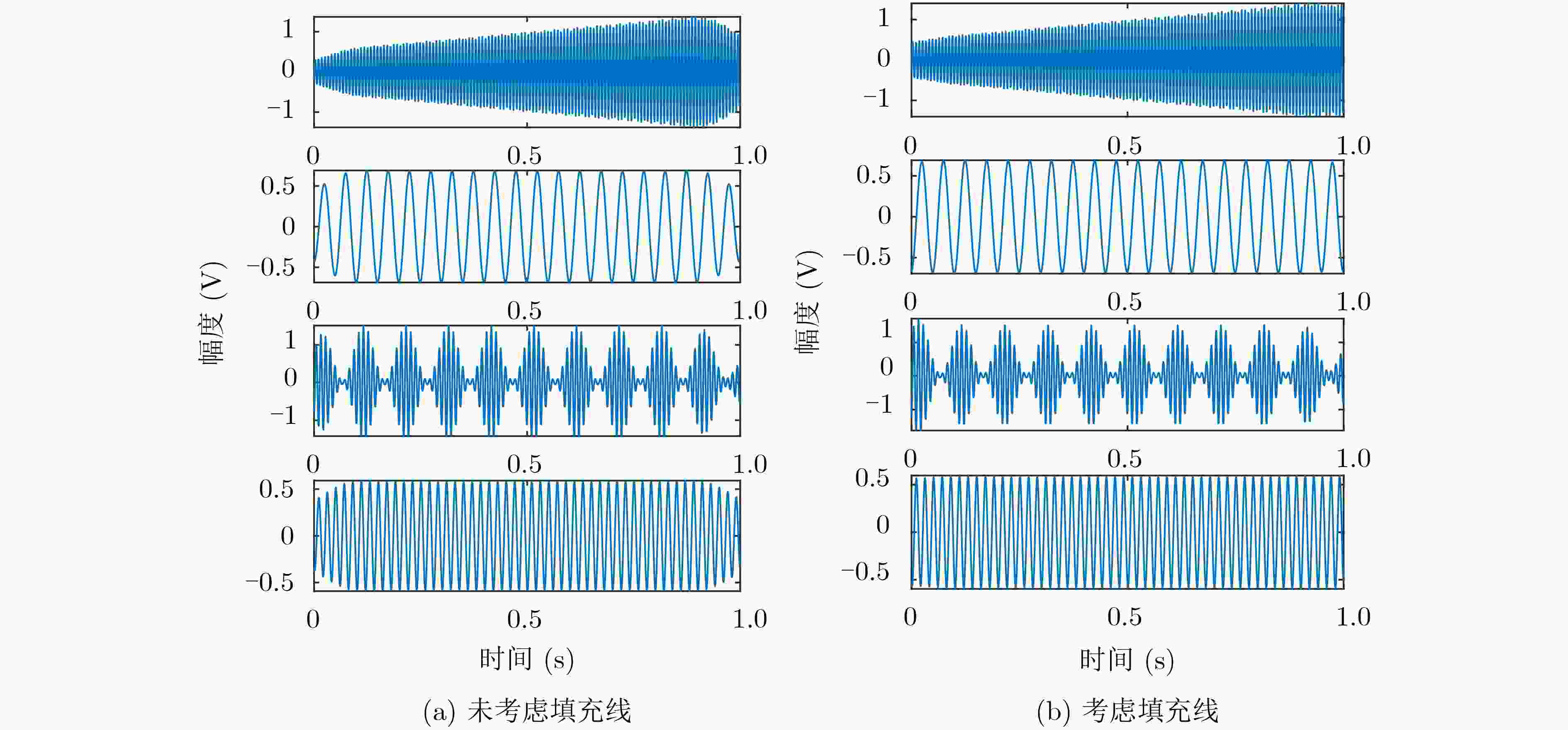
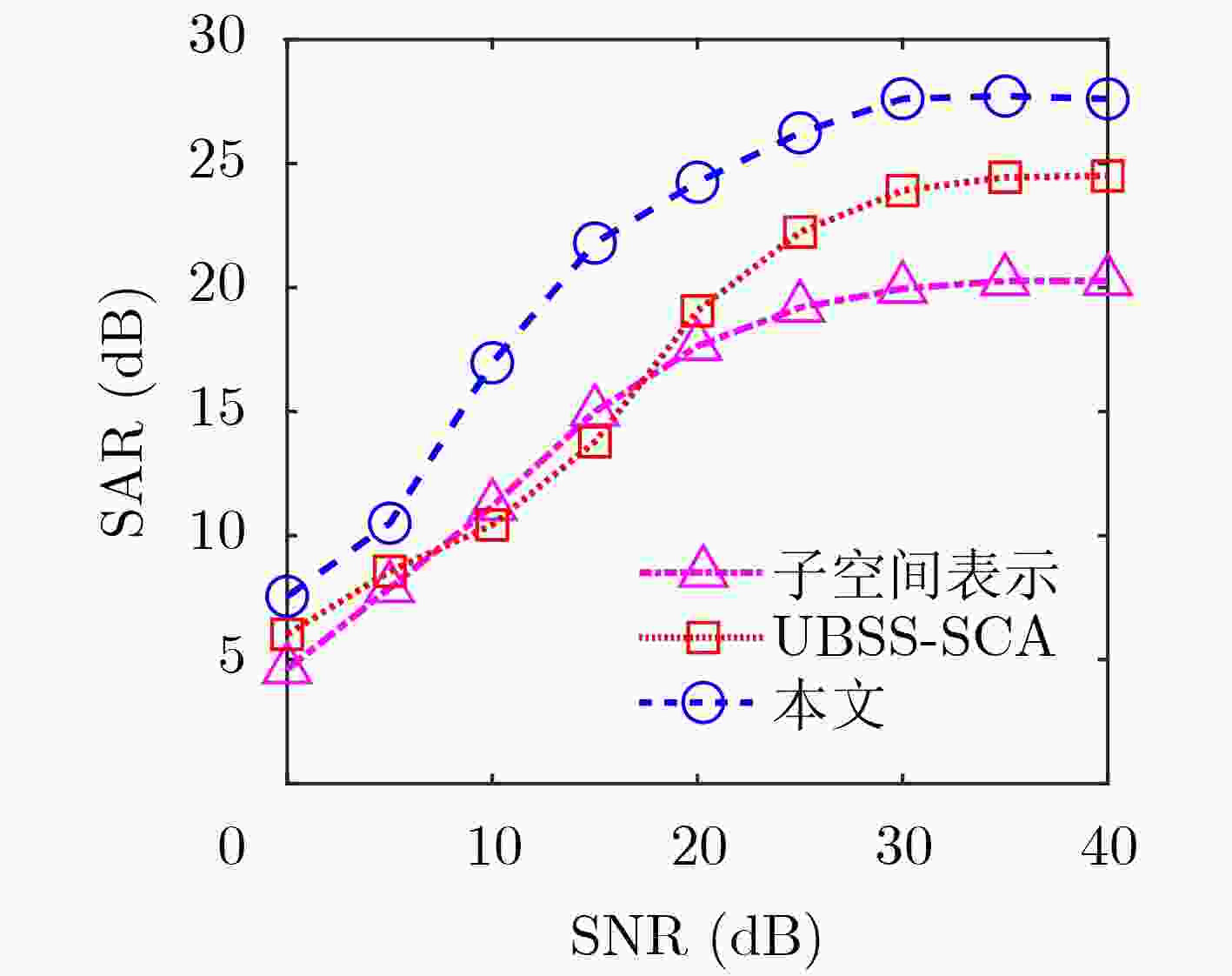
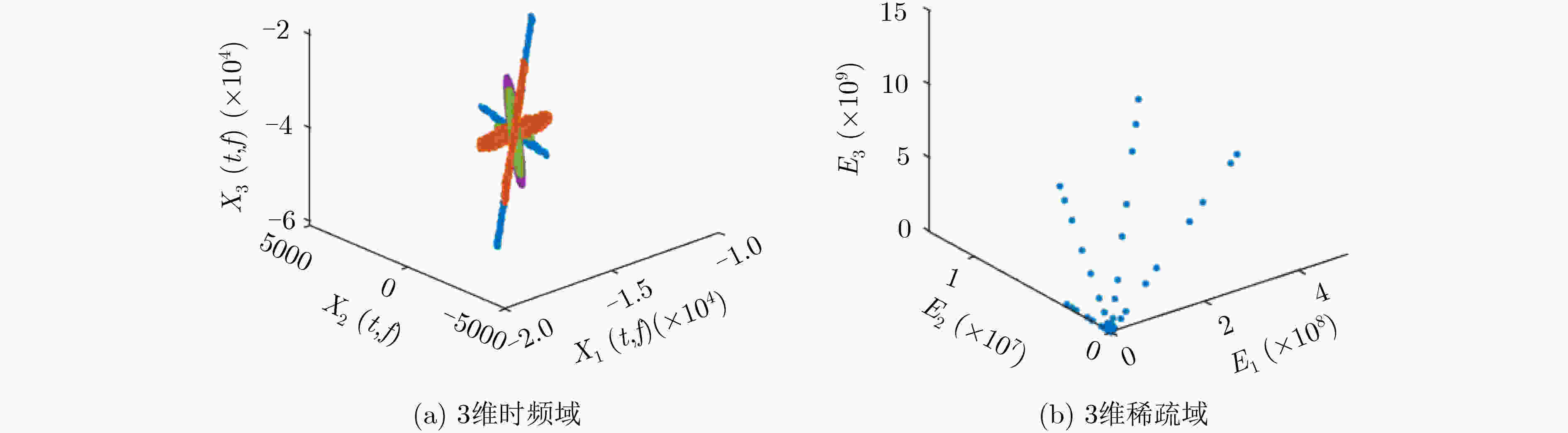
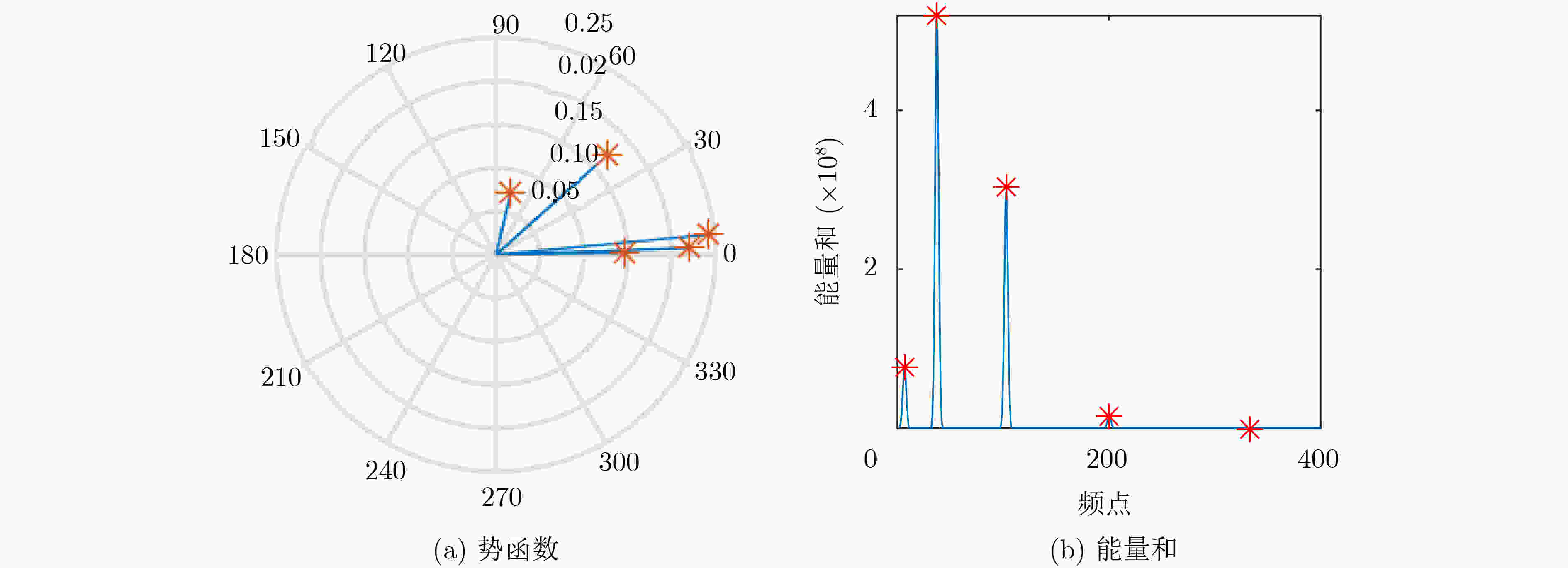
摘要: 为解决衰减延时混合信号的欠定盲源分离问题，该文研究了一种基于信源数估计的欠定盲源分离方法。首先，采用对时频域观测信号求能量来构造稀疏域；其次，在能量域中利用势函数估计信源数；再次，根据信源数将能量和峰值对应的频点筛选出来预测时频掩码从而获得估计信源的短时频谱；最后，填充线用来解决时域分离信号的边界效应问题。实验表明，所提方法可以有效分离衰减延时混合的模拟信号，并且在不同信噪比下优于稀疏聚类算法和子空间法；此外，在对实测悬臂梁锤击测试的过程中可以估计出模态阶数并且准确识别出结构的各阶模态固有频率。
- 欠定盲源分离 /
- 衰减时延混合信号 /
- 势函数 /
- 掩码预测 /
- 填充线
Abstract: In order to solve the problem of underdetermined blind source separation for attenuated and time-delayed mixtures of multiple sources, the approach based on source number estimation is proposed. Firstly, the sparse domain is constructed by calculating the energy of observations in time-frequency domain. Secondly, the potential function is used to estimate the number of sources in the energy domain. Thirdly, the frequency points corresponding to the peak of energy sum are filtered out to predict the time-frequency mask and then the spectrum of the estimated sources are obtained. Finally, the padding line is utilized to solve the boundary effect problem of time-domain separated signals. Experimental results demonstrate that the proposed method can effectively recover the simulated sources with time-delayed mixtures in underdetermined case, and is superior to sparse clustering algorithm and subspace method under different signal to noise ratios. In addition, the proposed method can estimate the modal order and identify the natural frequency of monomodal response successfully in the process of hammering test of the actual cantilever beam.
- Underdetermined blind source separation /
- Attenuated and time-delayed mixtures /
- Potential function /
- Binary mask prediction /
- Padding line

HTML全文

图 1 模拟信号时域波形

下载: 全尺寸图片幻灯片

图 2 模拟信号散点图

下载: 全尺寸图片幻灯片

图 3 峰值分布情况

下载: 全尺寸图片幻灯片

图 4 分离信号时域

下载: 全尺寸图片幻灯片

图 5 3种算法分离性能对比

下载: 全尺寸图片幻灯片

图 6 观测信号时域波形和频谱

下载: 全尺寸图片幻灯片

图 7 实测信号散点图

下载: 全尺寸图片幻灯片

图 8 测试实验中峰值分布情况

下载: 全尺寸图片幻灯片

图 9 估计源信号时域和频域

下载: 全尺寸图片幻灯片

表 1 固有频率估计结果(Hz)

模态	理论值	文献[24]	Subspace^[17]	UBSS-SCA^[18]	本文
1st	8.9	10.07 (13.15%)	9.96 (11.91%)	9.82 (10.34%)	8.95 (0.56%)
2nd	55.78	56.27 (0.88%)	56.43 (1.17%)	55.94 (0.29%)	55.87 (0.16%)
3rd	156.20	155.67 (0.34%)	155.65 (0.35%)	155.61 (0.38%)	156.43 (0.15%)
4th	306.09	304.18 (0.62%)	304.59 (0.49%)	304.57 (0.49%)	306.11 (0.007%)
5th	505.84	500.90 (0.98%)	502.62 (0.64%)	501.03 (0.95%)	505.38 (0.09%)

下载: 导出CSV

参考文献(24)

[1]	ZHOU Wenliang and CHELIDZE D. Blind source separation based vibration mode identification[J]. Mechanical Systems and Signal Processing, 2007, 21(8): 3072–3087. doi: 10.1016/j.ymssp.2007.05.007
[2]	BOFILL P and ZIBULEVSKY M. Underdetermined blind source separation using sparse representations[J]. Signal Processing, 2001, 81(11): 2353–2362. doi: 10.1016/S0165-1684(01)00120-7
[3]	LI Yuanqing, AMARI S, CICHOCKI A, et al. Underdetermined blind source separation based on sparse representation[J]. IEEE Transactions on Signal Processing, 2006, 54(2): 423–437. doi: 10.1109/TSP.2005.861743
[4]	吕晓德, 孙正豪, 刘忠胜, 等. 基于二阶统计量盲源分离算法的无源雷达同频干扰抑制研究[J]. 电子与信息学报, 2020, 42(5): 1288–1296. doi: 10.11999/JEIT190178 LÜ Xiaode, SUN Zhenghao, LIU Zhongsheng, et al. Research on suppressing co-channel interference of passive radar based on blind source separation using second order statistics[J]. Journal of Electronics &Information Technology, 2020, 42(5): 1288–1296. doi: 10.11999/JEIT190178
[5]	李扬, 张伟涛, 楼顺天. 基于联合对角化的声信号深度卷积混合盲分离方法[J]. 电子与信息学报, 2019, 41(12): 2951–2956. doi: 10.11999/JEIT190067 LI Yang, ZHANG Weitao, and LOU Shuntian. Deep convolution blind separation of acoustic signals based on joint diagonalization[J]. Journal of Electronics &Information Technology, 2019, 41(12): 2951–2956. doi: 10.11999/JEIT190067
[6]	LV Zhao, ZHANG Beibei, WU Xiaopei, et al. A permutation algorithm based on dynamic time warping in speech frequency-domain blind source separation[J]. Speech Communication, 2017, 92: 132–141. doi: 10.1016/j.specom.2017.06.007
[7]	GUO Qiang, RUAN Guoqing, and QI Liangang. A complex-valued mixing matrix estimation algorithm for underdetermined blind source separation[J]. Circuits, Systems, and Signal Processing, 2018, 37(8): 3206–3226. doi: 10.1007/s00034-018-0796-6
[8]	REJU V G, KOH S N, and SOON I Y. Underdetermined convolutive blind source separation via time-frequency masking[J]. IEEE Transactions on Audio, Speech, and Language Processing, 2010, 18(1): 101–116. doi: 10.1109/TASL.2009.2024380
[9]	ZHEN Liangli, PENG Dezhong, YI Zhang, et al. Underdetermined blind source separation using sparse coding[J]. IEEE Transactions on Neural Networks and Learning Systems, 2017, 28(12): 3102–3108. doi: 10.1109/TNNLS.2016.2610960
[10]	FU Weihong, CHEN Jiehu, and YANG Bo. Source recovery of underdetermined blind source separation based on SCMP algorithm[J]. IET Signal Processing, 2017, 11(7): 877–883. doi: 10.1049/iet-spr.2015.0100
[11]	ZHANG Liangjun, YANG Jie, GUO Zhiqiang, et al. Underdetermined blind source separation from time-delayed mixtures based on prior information exploitation[J]. Journal of Electrical Engineering and Technology, 2015, 10(5): 2179–2188. doi: 10.5370/JEET.2015.10.5.2179
[12]	YE Fang, CHEN Jie, GAO Lipeng, et al. A mixing matrix estimation algorithm for the time-delayed mixing model of the underdetermined blind source separation problem[J]. Circuits, Systems, and Signal Processing, 2019, 38(4): 1889–1906. doi: 10.1007/s00034-018-0930-5
[13]	付永庆, 郭慧, 苏东林, 等. 基于源数估计的无约束欠定盲源分离算法[J]. 哈尔滨工程大学学报, 2015, 36(5): 730–735. doi: 10.3969/j.issn.1006-7043.201308065 FU Yongqing, GUO Hui, SU Donglin, et al. Unconstrained underdetermined blind source separation algorithm based on the source number estimation[J]. Journal of Harbin Engineering University, 2015, 36(5): 730–735. doi: 10.3969/j.issn.1006-7043.201308065
[14]	YANG Zuyuan, TAN Beihai, ZHOU Guoxu, et al. Source number estimation and separation algorithms of underdetermined blind separation[J]. Science in China Series F: Information Sciences, 2008, 51(10): 1623–1632. doi: 10.1007/s11432-008-0138-6
[15]	CHENG Wei, LEE S, ZHANG Zhousuo, et al. Independent component analysis based source number estimation and its comparison for mechanical systems[J]. Journal of Sound and Vibration, 2012, 331(23): 5153–5167. doi: 10.1016/j.jsv.2012.06.021
[16]	LU Jiantao, CHENG Wei, HE Dong, et al. A novel underdetermined blind source separation method with noise and unknown source number[J]. Journal of Sound and Vibration, 2019, 457: 67–91. doi: 10.1016/j.jsv.2019.05.037
[17]	KIM S G and YOO C D. Underdetermined blind source separation based on subspace representation[J]. IEEE Transactions on Signal Processing, 2009, 57(7): 2604–2614. doi: 10.1109/TSP.2009.2017570
[18]	HE Changbo, LI Hongkun, and ZHAO Xinwei. Weak characteristic determination for blade crack of centrifugal compressors based on underdetermined blind source separation[J]. Measurement, 2018, 128: 545–557. doi: 10.1016/j.measurement.2018.06.047
[19]	肖明, 谢胜利, 傅予力. 基于频域单源区间的具有延迟的欠定盲分离[J]. 电子学报, 2007, 35(12): 2279–2283. doi: 10.3321/j.issn:0372-2112.2007.12.008 XIAO Ming, XIE Shengli, and FU Yuli. Underdetermined blind delayed source separation based on single source intervals in frequency domain[J]. Acta Electronica Sinica, 2007, 35(12): 2279–2283. doi: 10.3321/j.issn:0372-2112.2007.12.008
[20]	ZHANG Chaozhu, WANG Yu, JING Fulong, et al. Underdetermined blind source separation of synchronous orthogonal frequency hopping signals based on single source points detection[J]. Sensors, 2017, 17(9): 2074. doi: 10.3390/s17092074
[21]	LI Yibing, NIE Wei, and YE Fang. A complex mixing matrix estimation algorithm based on single source points[J]. Circuits, Systems, and Signal Processing, 2015, 34(11): 3709–3723. doi: 10.1007/s00034-015-0027-3
[22]	MUR A, DORMIDO R, DURO N, et al. An unsupervised method to determine the optimal number of independent components[J]. Expert Systems with Applications, 2017, 75: 56–62. doi: 10.1016/j.eswa.2017.01.015
[23]	VINCENT E, GRIBONVAL R, and FEVOTTE C. Performance measurement in blind audio source separation[J]. IEEE Transactions on Audio, Speech, and Language Processing, 2006, 14(4): 1462–1469. doi: 10.1109/TSA.2005.858005
[24]	YANG Kai, YU Kaiping, and LI Qiaofeng. Modal parameter extraction based on Hilbert transform and complex independent component analysis with reference[J]. Mechanical Systems and Signal Processing, 2013, 40(1): 257–268. doi: 10.1016/j.ymssp.2013.05.003