DOA Estimation Algorithm Based on Reduced-dimensional Beamspace with Real-valued ESPRIT for Monostatic MIMO Radar
-
摘要: 单基地多输入多输出(MIMO)雷达的波达方向(DOA)估计问题是近年来研究的热点。高维度的MIMO雷达数据，导致传统旋转不变性参数估计技术(ESPRIT)算法需要付出较大的运算代价。在低信噪比、低快拍数的条件下，传统ESPRIT算法性能会严重下降。为了克服传统ESPRIT算法的以上缺点，该文提出一种降维波束空间的实值ESPRIT算法。该算法通过转换矩阵，将高维度MIMO雷达数据转换到低维度的数据，从而去除数据中的冗余。然后再将低维数据变换到波束空间，构造实值旋转不变性等式，用以估计目标的角度。仿真结果表明，在低信噪比和低快拍数时，相比于传统ESPRIT算法，该文所提方法具有更好的角度估计性能和更少的运算量。Abstract: The Direction Of Arrival (DOA) estimation is a hot topic for a monostatic Multiple Input Multiple Output (MIMO) radar in recent years. The conventional Estimation of Signal Parameters via Rotational Invariance Technique (ESPRIT) algorithms need to pay much computation cost because of the high-dimensional MIMO radar data. When the Signal-to-Noise Ratio (SNR) is low and the number of sample are small, the performance of the conventional ESPRIT algorithms degrades seriously. To overcome the disadvantages of conventional ESPRIT algorithms, a novel algorithm which is called as reduced-dimensional beamspace with real-valued ESPRIT for monostatic MIMO radar is proposed. To eliminate the redundancy, the high-dimensional MIMO radar data is transformed into the low-dimensional data through the transformation matrix. To reduce further the computation complexity, the low-dimensional data is transformed into beamspace. Then the real-valued rotation invariance equation is constructed to estimate the target’s DOA. Simulation results show the proposed algorithm has better angle estimation performance and less computation burden than traditional ESPRIT algorithms.
-
[1] HAIMOVICH A M, BLUM R S, and CIMINI L J. MIMO Radar with Widely Separated antennas[J]. IEEE Signal Processing Magazine, 2008, 25(1): 116–129. doi: 10.1109/MSP.2008.4408448 [2] LI Jian and STOICA P. MIMO radar with colocated antennas[J]. IEEE Signal Processing Magazine, 2007, 24(5): 106–114. doi: 10.1109/MSP.2007.904812 [3] ZHAO Yongbo, SHUI Penglang, and LIU Hongwei. Computationally efficient DOA estimation for MIMO radar[C]. The 2nd International Congress on Image and Signal Processing, Tianjin, China, 2009: 1–3. doi: 10.1109/CISP.2009.5304414. [4] ZHANG X, HUANG Y, CHEN C, et al. Reduced-complexity Capon for direction of arrival estimation in a monostatic multiple-input multiple-output radar[J]. IET Radar, Sonar & Navigation, 2012, 6(8): 796–801. doi: 10.1049/iet-rsn.2011.0343 [5] JINLI C, HONG G, and WEIMIN S. Angle estimation using ESPRIT without pairing in MIMO radar[J]. Electronics Letters, 2008, 44(24): 1422–1423. doi: 10.1049/el:20089089 [6] ZHANG X and XU D. Low-complexity ESPRIT-based DOA estimation for colocated MIMO radar using reduced-dimension transformation[J]. Electronics Letters, 2011, 47(4): 283–284. doi: 10.1049/el.2010.3279 [7] 文才, 王彤. 单基地MIMO雷达降维酉ESPRIT算法[J]. 系统工程与电子技术, 2014, 36(6): 1062–1067. doi: 10.3969/j.issn.1001-506X.2014.06.08WEN Cai and WANG Tong. Reduced-dimensional unitary ESPRIT algorithm for monostatic MIMO radar[J]. Systems Engineering and Electronics, 2014, 36(6): 1062–1067. doi: 10.3969/j.issn.1001-506X.2014.06.08 [8] ZHANG Yu, ZHANG Gong, and WANG Xinhai. Computationally efficient DOA estimation for monostatic MIMO radar based on covariance matrix reconstruction[J]. Electronics Letters, 2017, 53(2): 111–113. doi: 10.1049/el.2016.3818 [9] 徐保庆, 赵永波, 庞晓娇. 基于实值处理的联合波束域双基地MIMO雷达测角算法[J]. 电子与信息学报, 2019, 41(7): 1721–1727. doi: 10.11999/JEIT180766XU Baoqing, ZHAO Yongbo, and PANG Xiaojiao. Joint real-valued beamspace-based method for angle estimation in bistatic MIMO radar[J]. Journal of Electronics &Information Technology, 2019, 41(7): 1721–1727. doi: 10.11999/JEIT180766 [10] LI Jianfeng, HE Yi, HE Lang, et al. DOD and DOA estimation for MIMO radar based on combined MUSIC and sparse Bayesian learning[C]. 2019 International Applied Computational Electromagnetics Society Symposium - China (ACES), Nanjing, China, 2019: 1–2. doi: 10.23919/ACES48530.2019.9060555. [11] YANG Zai and XIE Lihua. On gridless sparse methods for multi-snapshot DOA estimation[C]. 2016 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Shanghai, China, 2016: 3236–3240. doi: 10.1109/ICASSP.2016.7472275. [12] YANG Zai, XIE Lihua, and ZHANG Cishen. Off-grid direction of arrival estimation using sparse bayesian inference[J]. IEEE Transactions on Signal Processing, 2013, 61(1): 38–43. doi: 10.1109/TSP.2012.2222378 [13] WEN Fangqing, HUANG Dongmei, WANG Ke, et al. DOA estimation for monostatic MIMO radar using enhanced sparse Bayesian learning[J]. The Journal of Engineering, 2018, 2018(5): 268–273. doi: 10.1049/joe.2017.0872 [14] MAO Chenxing and WEN Fangqing. Off-grid DOA estimation for Colocated MIMO radar via sparse Bayesian learning[C]. 2019 International Applied Computational Electromagnetics Society Symposium - China (ACES), Nanjing, China, 2019: 1–2. doi: 10.23919/ACES48530.2019.9060628. [15] LIU Tingting, WEN Fangqing, ZHANG Lei, et al. Off-grid DOA estimation for Colocated MIMO radar via reduced-complexity sparse Bayesian learning[J]. IEEE Access, 2019, 7: 99907–99916. doi: 10.1109/ACCESS.2019.2930531 [16] CHEN Fangfang, ZHANG Jinghao, and DAI Jisheng. DOD and DOA estimation for bistatic MIMO radars with sparse Bayesian learning[C]. 2018 International Workshop on Antenna Technology (iWAT), Nanjing, China, 2018: 1–4. doi: 10.1109/IWAT.2018.8379194. [17] ZOLTOWSKI M D, KAUTZ G M, and SILVERSTEIN S D. Beamspace root-MUSIC[J]. IEEE Transactions on Signal Processing, 1993, 41(1): 344. doi: 10.1109/TSP.1993.193151 [18] ZOLTOWSKI M D, HAARDT M, and MATHEWS C P. Closed-form 2-D angle estimation with rectangular arrays in element space or beamspace via unitary ESPRIT[J]. IEEE Transactions on Signal Processing, 1996, 44(2): 316–328. doi: 10.1109/78.485927 [19] FORSTER P and VEZZOSI G. Application of spheroidal sequences to array processing[C]. 1987 IEEE International Conference on Acoustics, Speech, and Signal Processing, Dallas, USA, 1987: 2268–2271. doi: 10.1109/ICASSP.1987.1169421. -
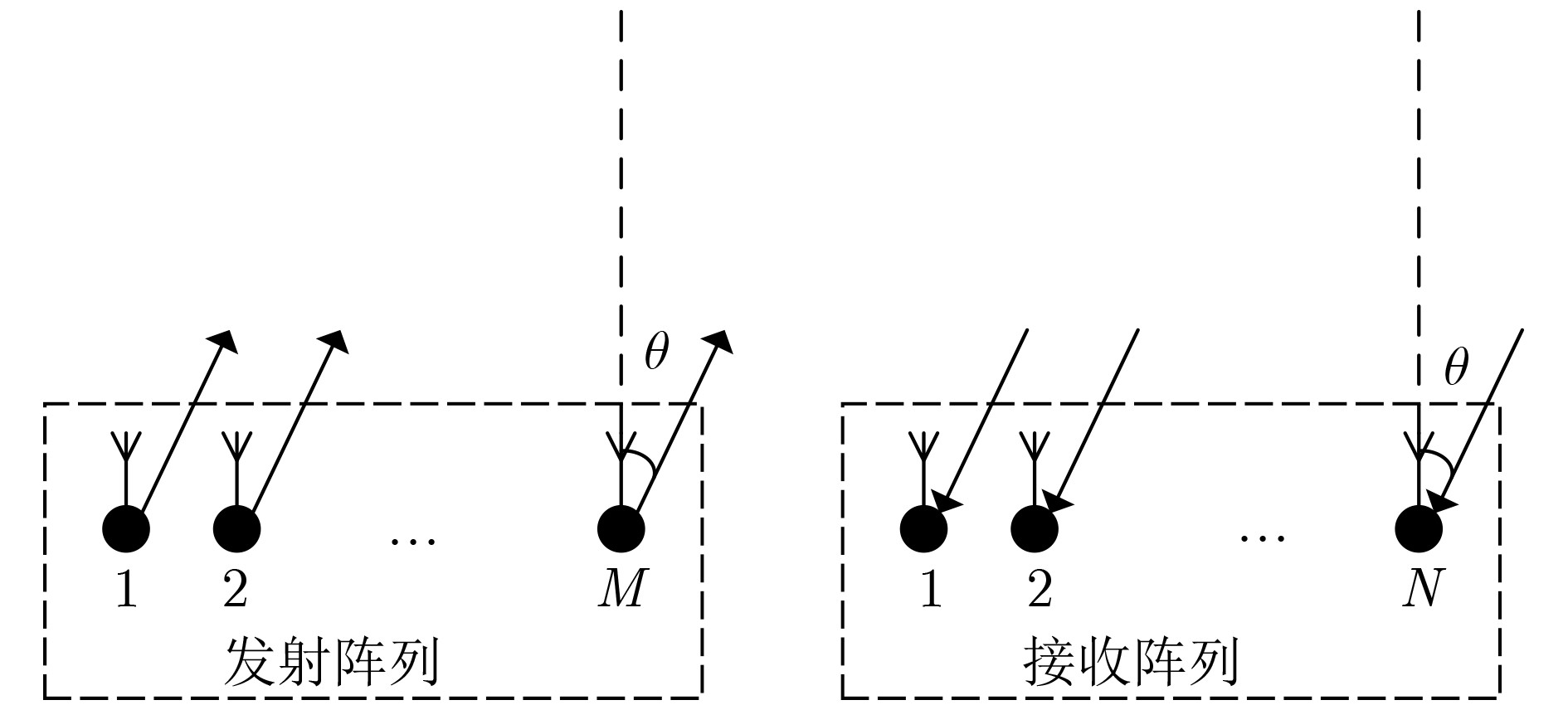
下载:
图(8)
计量
- 文章访问数: 1063
- HTML全文浏览量: 597
- PDF下载量: 128
- 被引次数: 0
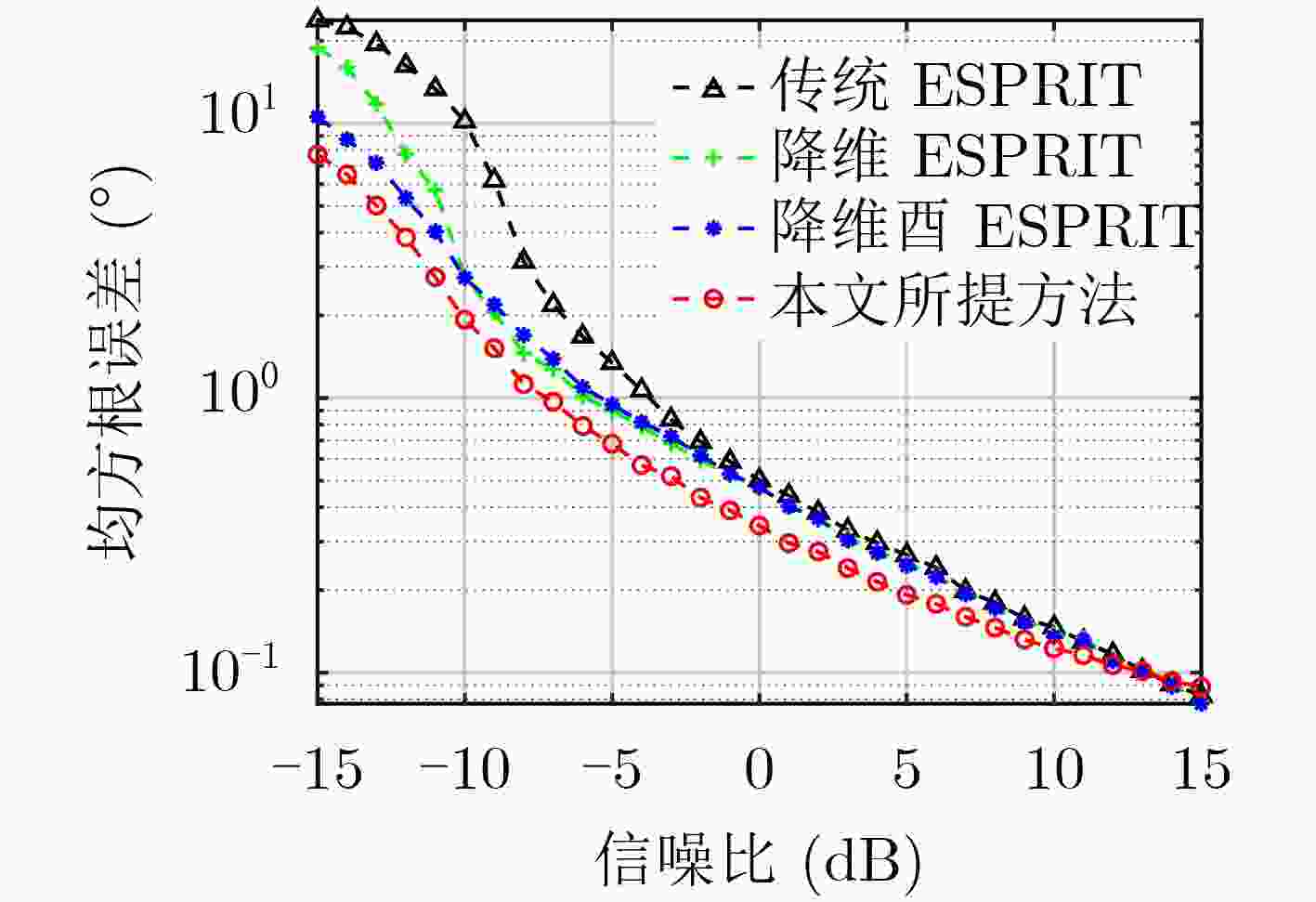
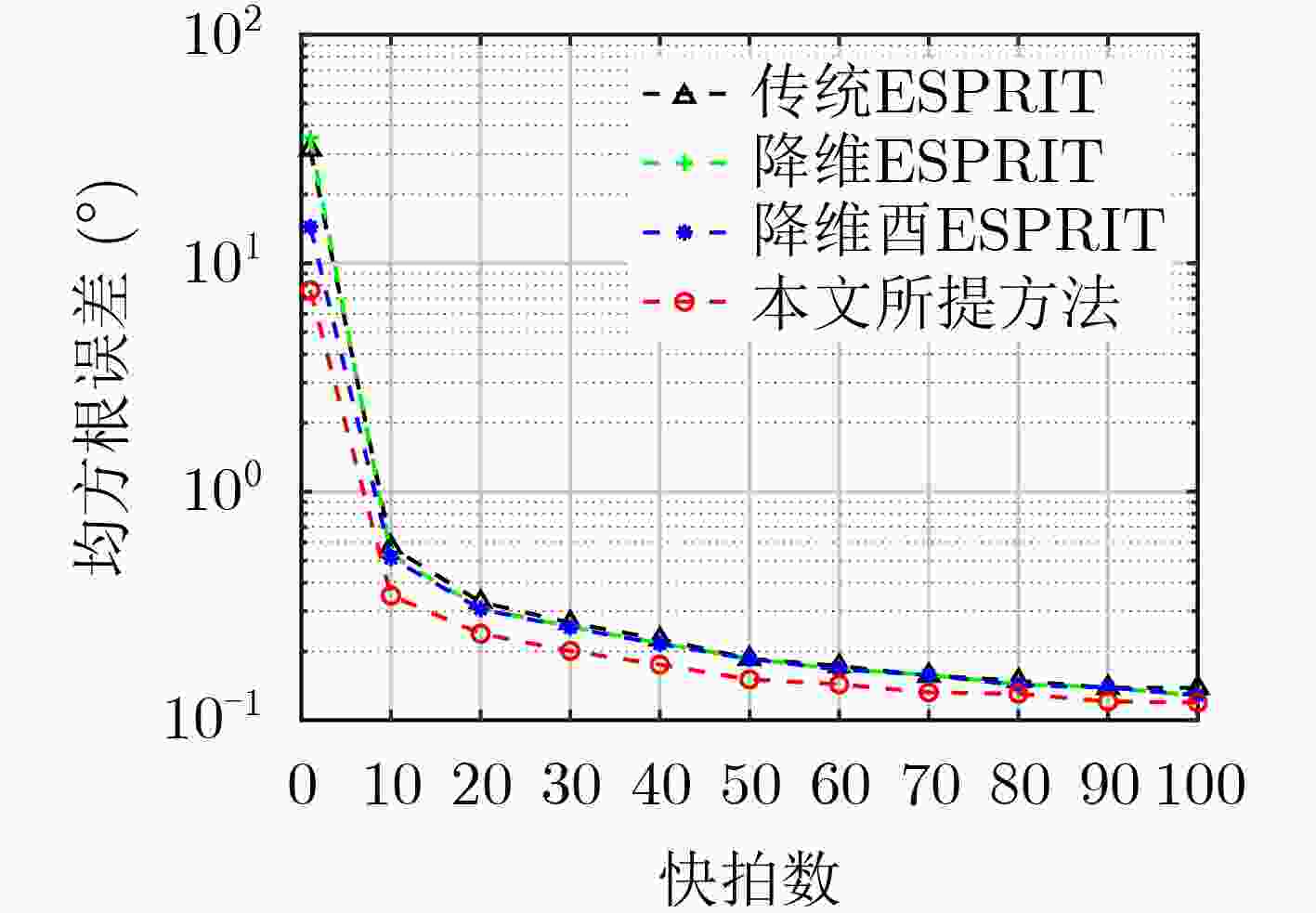
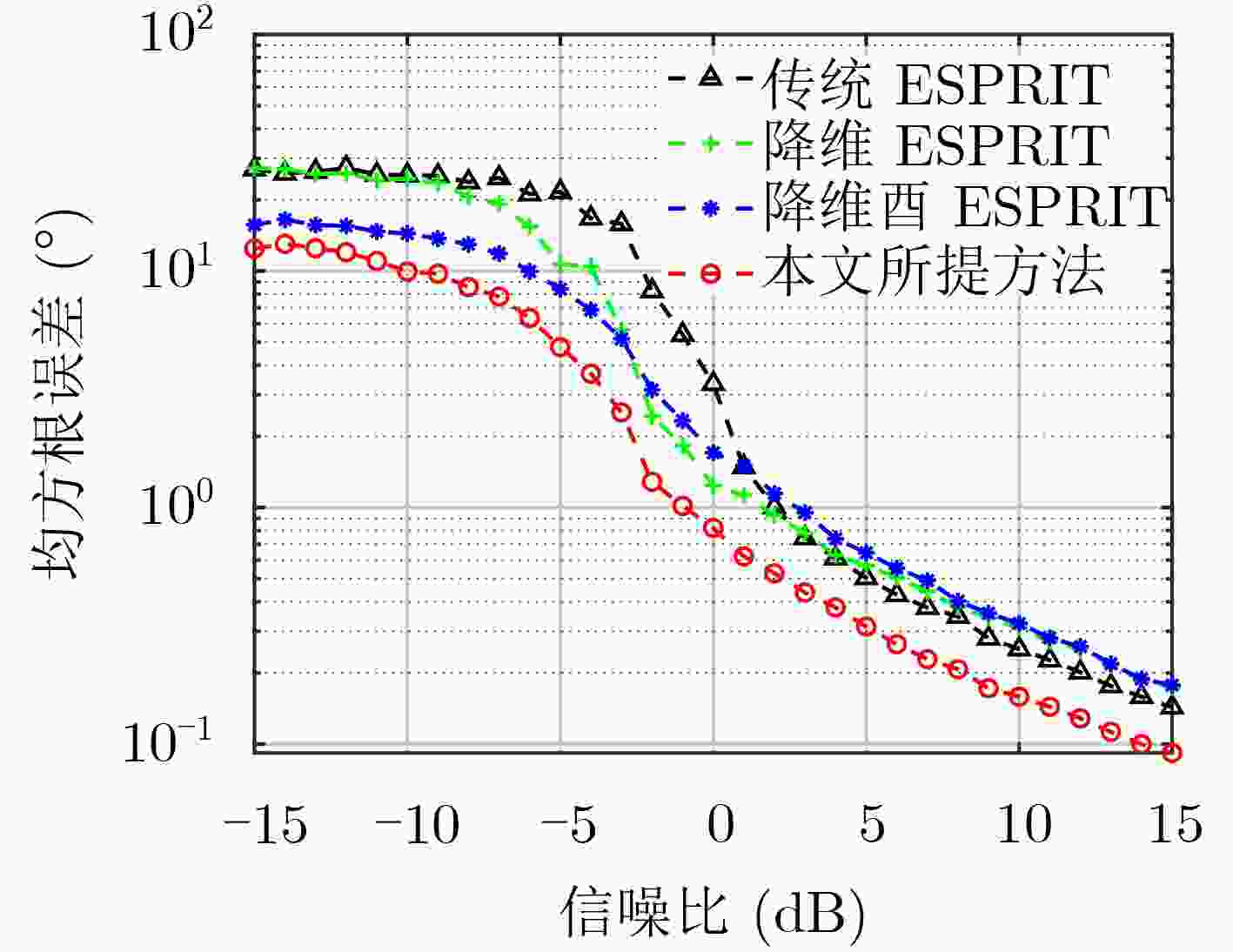
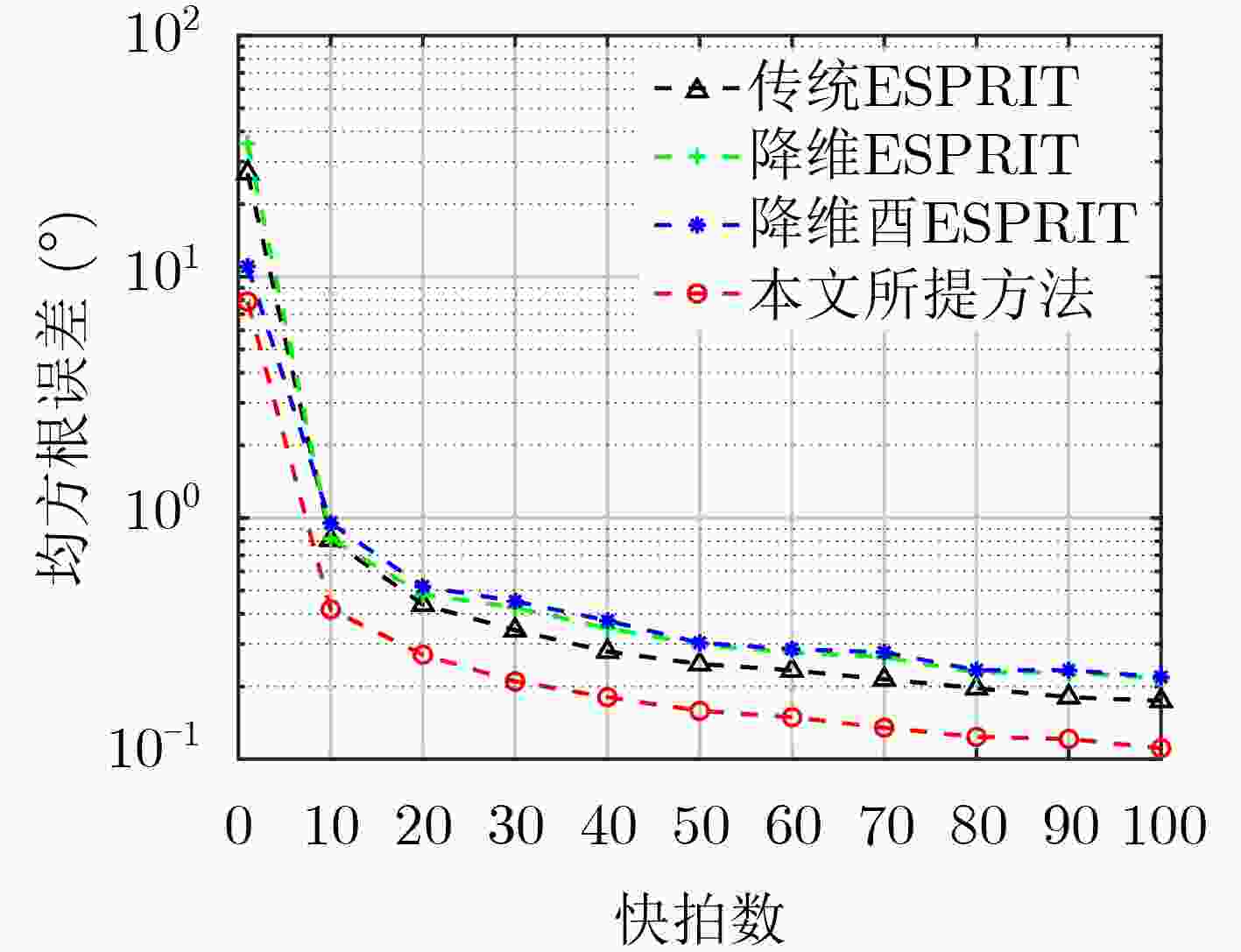
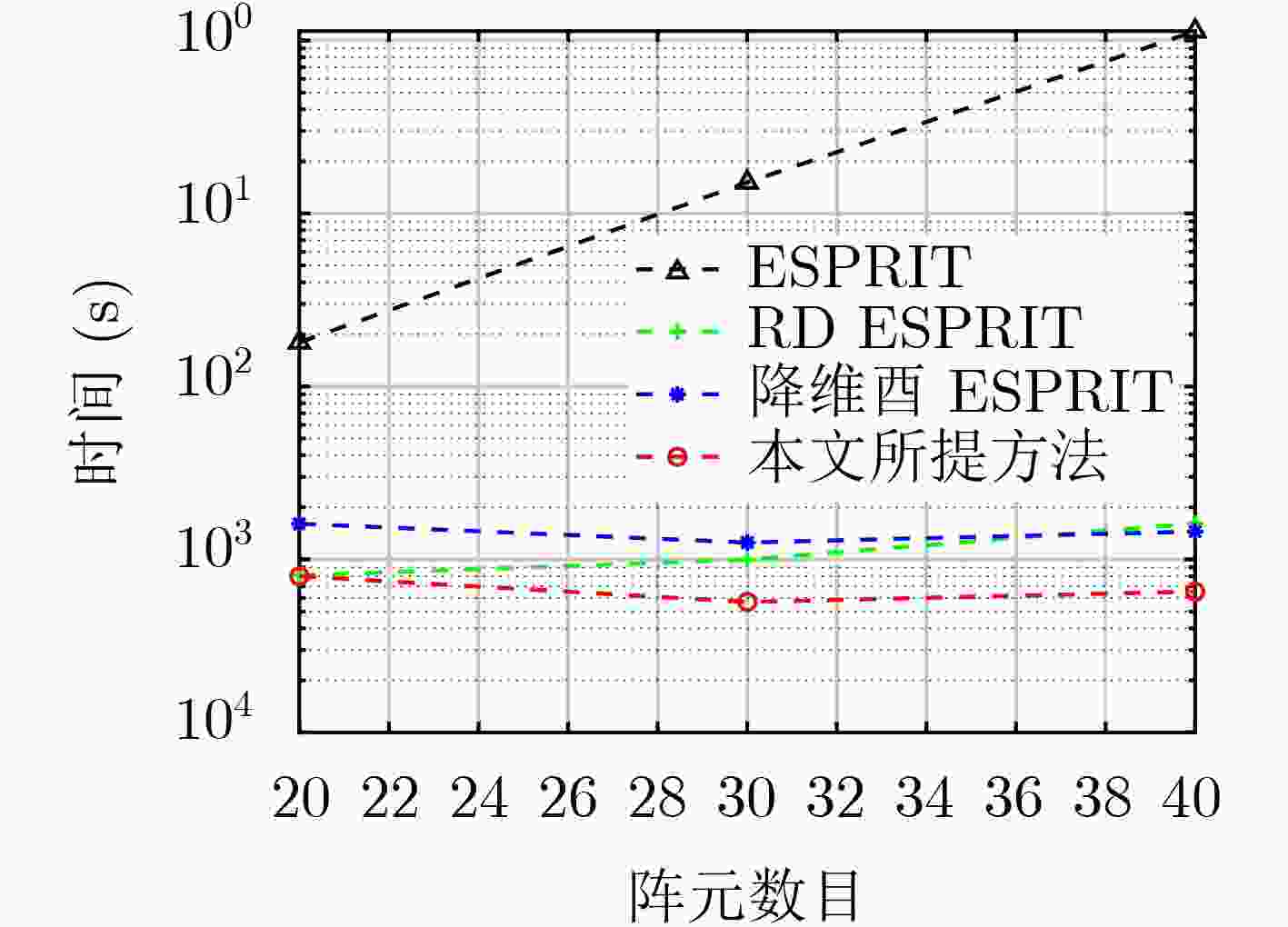
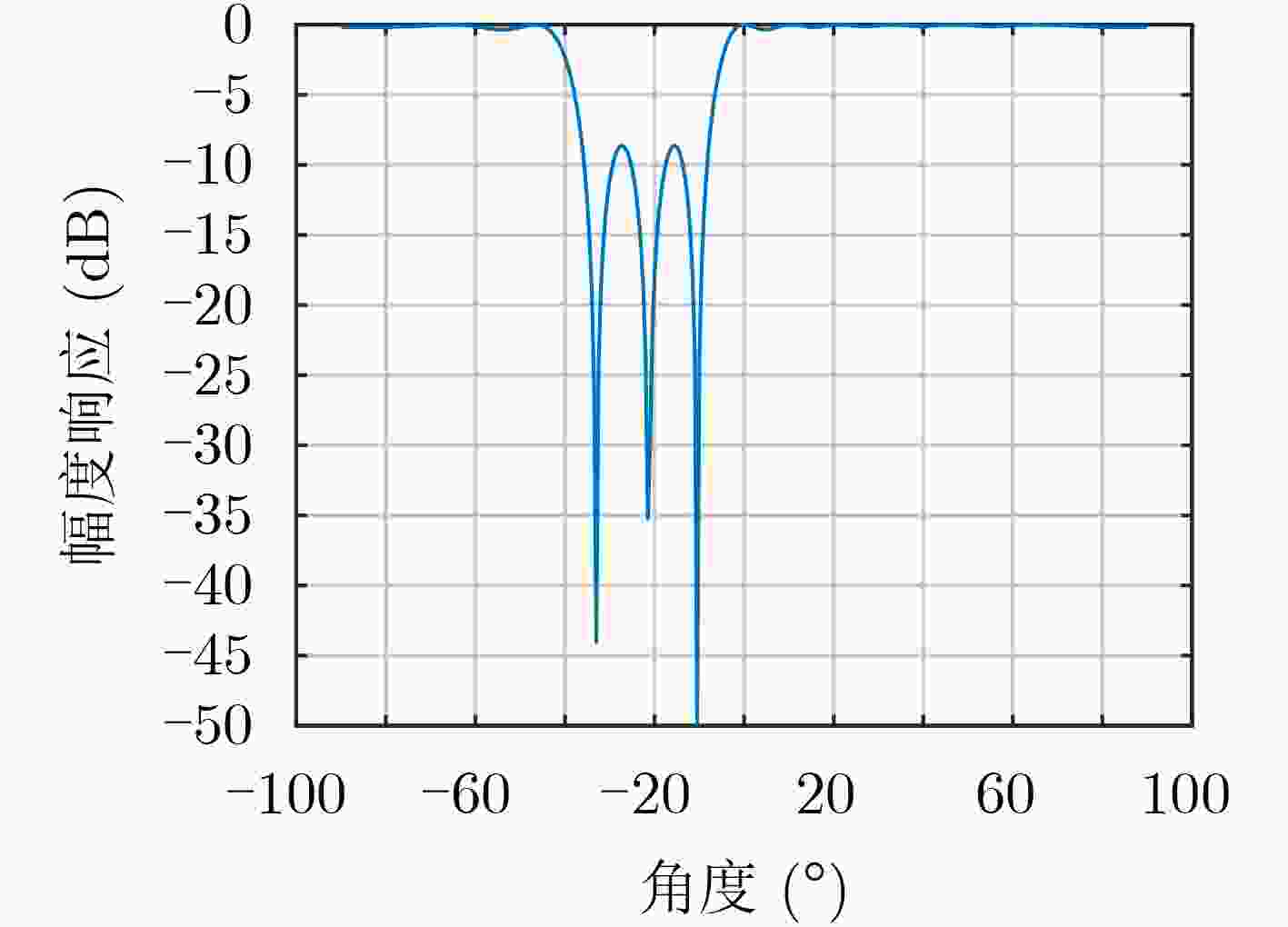
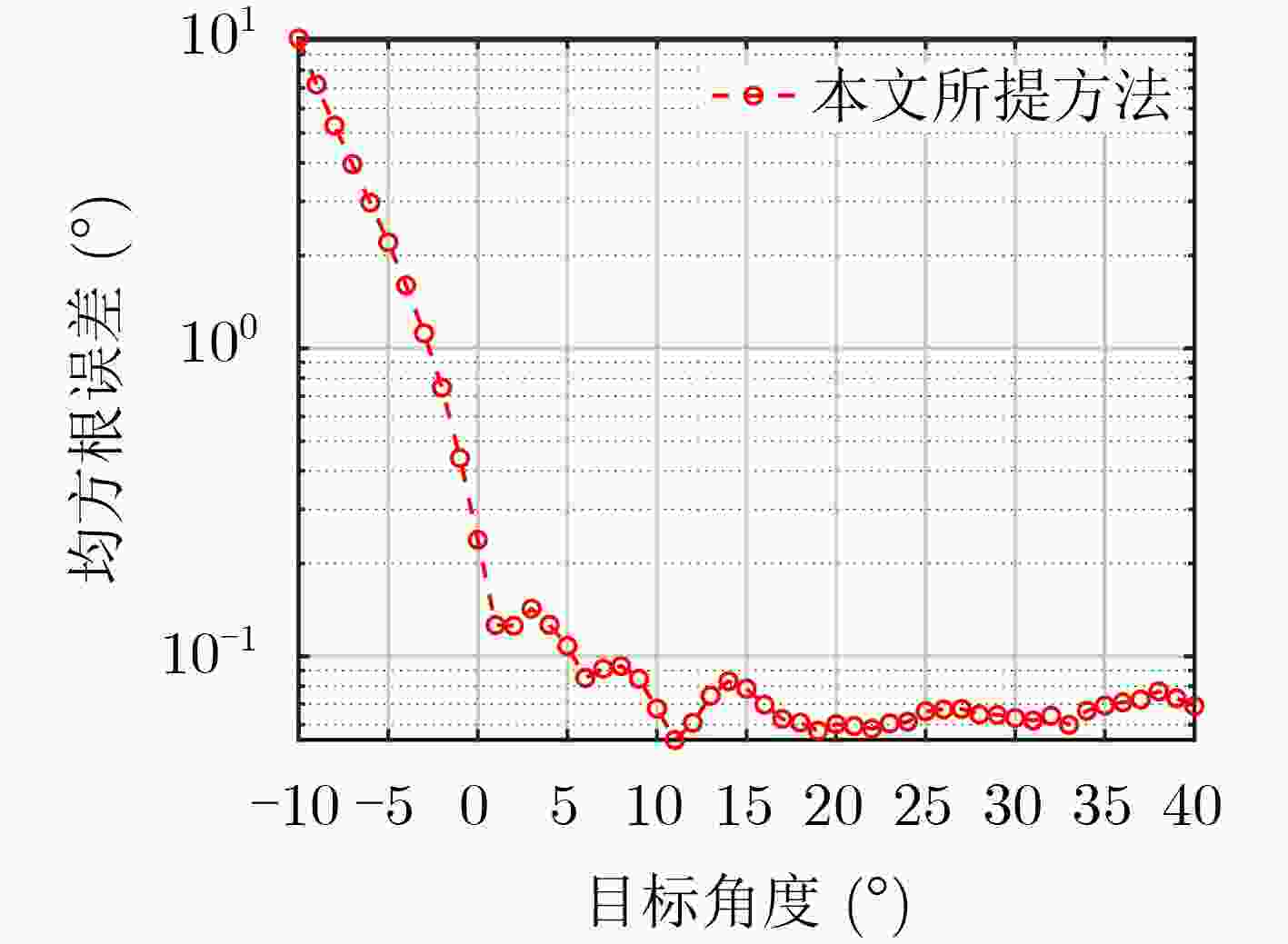
下载:
