Novel Adaptive Generalized Eigenvector Estimation Algorithm and Its Characteristic Analysis
-
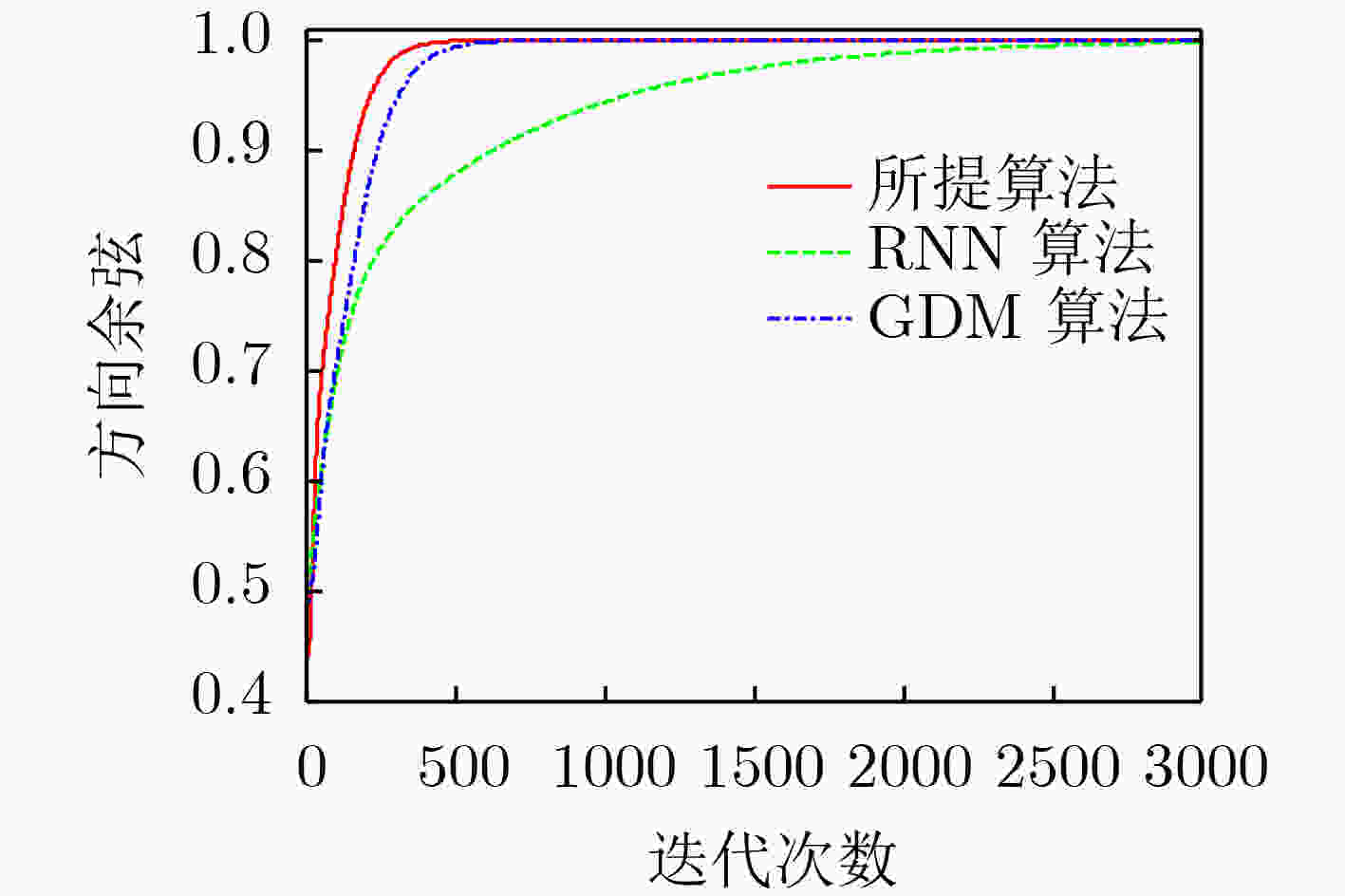
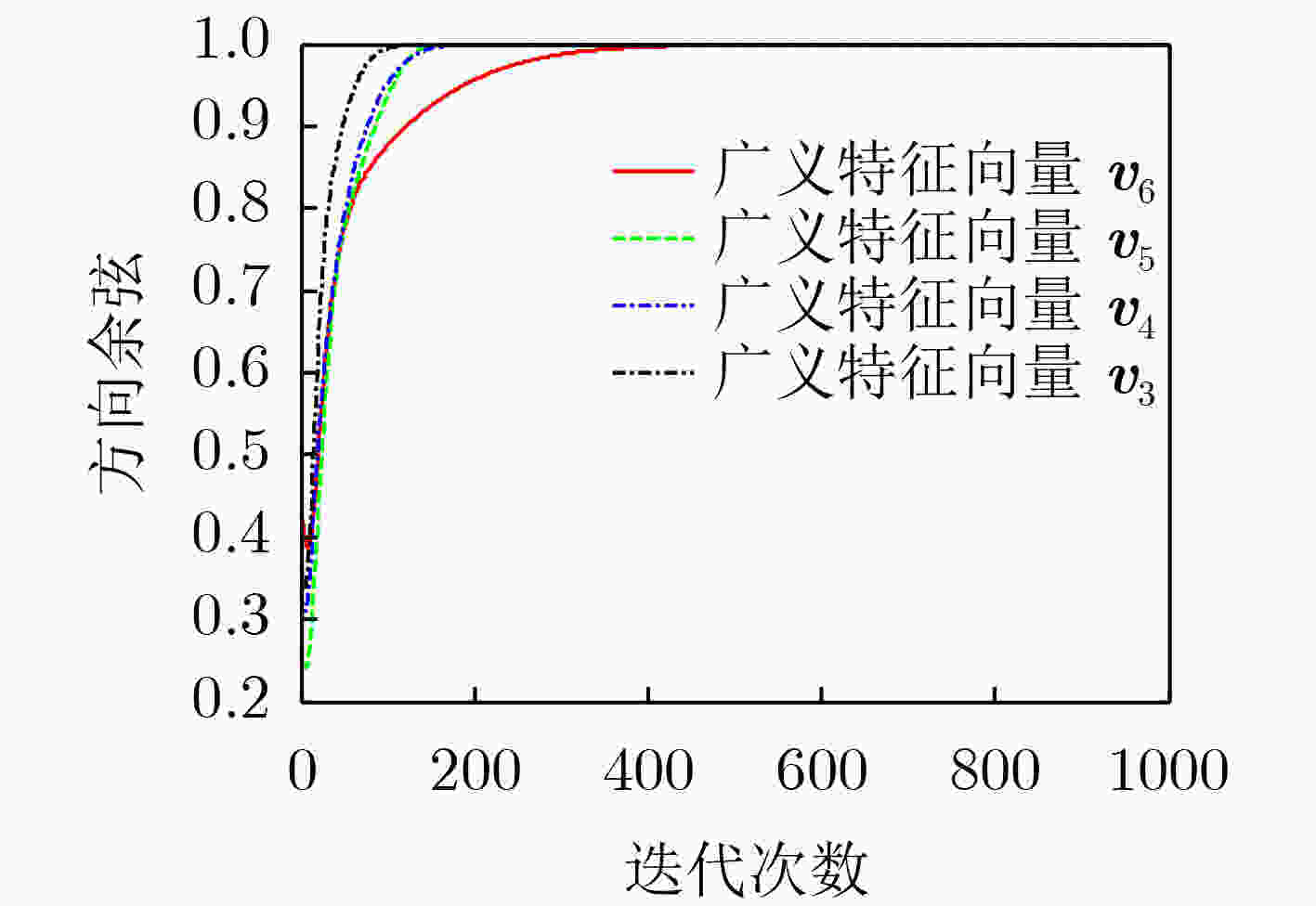
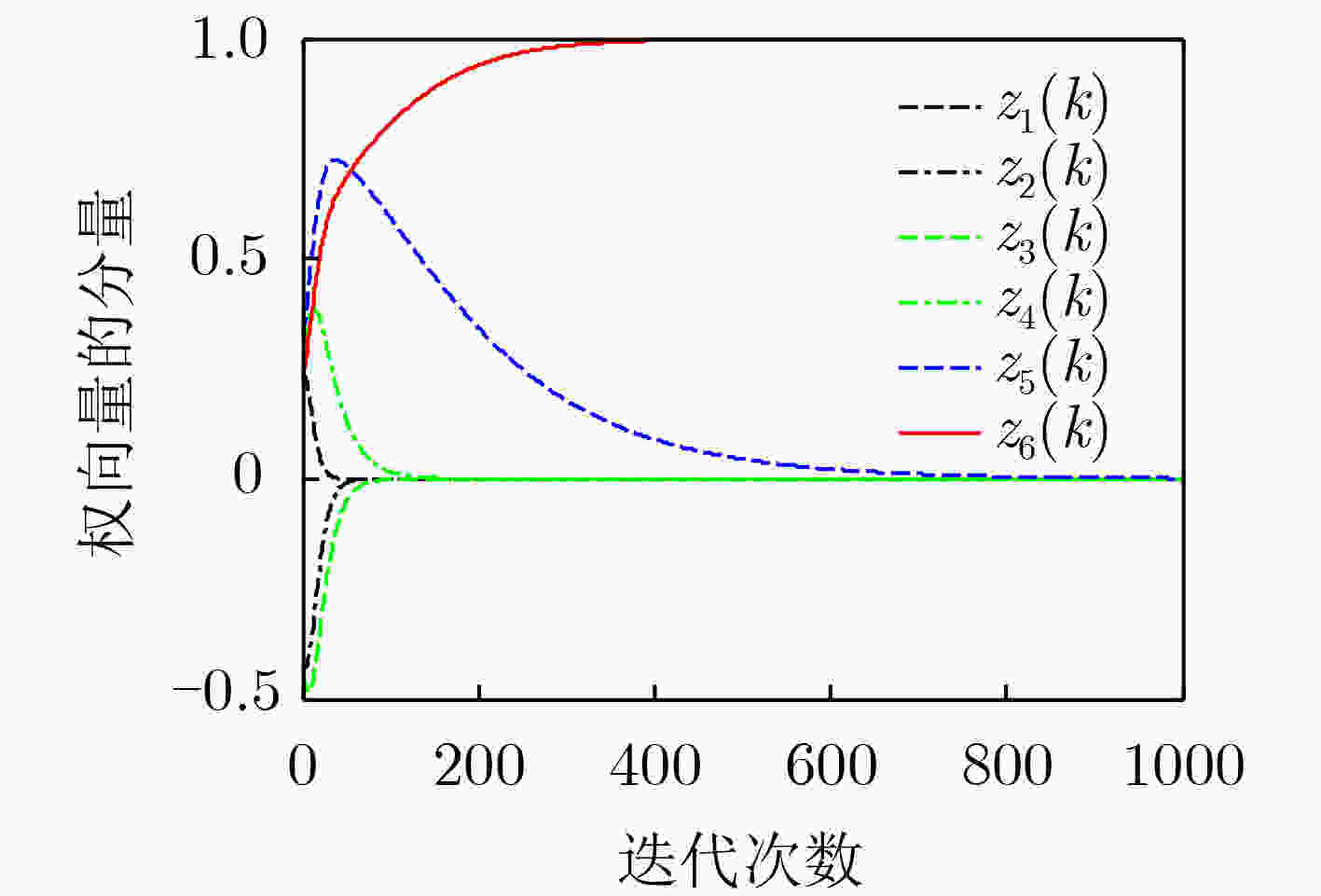
摘要: 为了发展快速稳定的广义特征向量估计算法,该文提出基于神经网络的新型单维广义特征向量估计算法;通过分析该算法的所有平衡点证明了当且仅当神经网络权向量等于最小广义特征值对应的广义特征向量时该算法达到稳定状态;利用确定性离散时间分析方法完成了所提算法的动态特性分析,给出了保证算法收敛的边界条件;通过膨胀技术将单维算法扩展为多维广义特征向量估计算法,该算法可以根据实际需要增加提取广义特征向量的数量。仿真实验表明所提算法具有很好地收敛性,而且收敛速度优于一些现有算法。Abstract: In order to develop fast and stable algorithm for estimating generalized eigenvector, a novel neuron-based algorithm is proposed for extracting the single generalized eigenvector. Through analyzing all of the stationary points, it is proved that the single estimation algorithm reaches the steady state if and only if the weight vector of the neural network is equal to the generalized eigenvector corresponding to the smallest generalized eigenvalue of a matrix pencil. The dynamic analysis of the single estimation algorithm is accomplished by the deterministic discrete time method and some boundary conditions are also obtained to guarantee the algorithm’s convergence. Trough applying the inflation technique, the single generalized eigenvector estimation algorithm is extended into a multiple generalized eigenvector estimation algorithm, and the number of the generalized eigenvectors can be increased according to actual requirement. Simulation experiments results prove that the proposed algorithm has good convergence, and the convergence speed is better than some existing algorithms.
-
Key words:
- Generalized eigenvector /
- Stability analysis /
- Dynamic analysis /
- Multiple extraction
-
表 1 多维广义特征向量估计步骤
初始化:设置学习因子$\eta $和广义特征值上界$\sigma $,产生初始化权向量${\boldsymbol{w}}(0)$ 迭代计算:令$d = 1,2, \cdots ,r$,其中$r$为需要估计广义特征向量的个数 步骤1:令$d = 1$,利用式(5)估计出第1个广义特征向量${{\boldsymbol{\bar v}}_n}$; 步骤2:令$d = d + 1$,利用式(11)计算出第$d$个广义特征向量${{\boldsymbol{\bar v}}_{n - d + 1}}$ $ {{\boldsymbol{w}}_d}(k + 1) = {{\boldsymbol{w}}_d}(k) + \eta \left[ { - \left( {2{\boldsymbol{w}}_d^{\rm{T}}(k){{\boldsymbol{R}}_x}{{\boldsymbol{w}}_d}(k) - 1} \right){\boldsymbol{R}}_x^{ - 1}{{\boldsymbol{R}}_{d,y}}{{\boldsymbol{w}}_d}(k) + {\boldsymbol{w}}_d^{\rm{T}}(k){{\boldsymbol{R}}_{d,y}}{{\boldsymbol{w}}_d}(k){{\boldsymbol{w}}_d}(k)} \right] $ (11) 其中
$ {{\boldsymbol{R}}_{d,y}} = {{\boldsymbol{R}}_y} + \sigma \displaystyle\sum\limits_{d = 1}^{d - 1} {{{\boldsymbol{R}}_x}{{{\boldsymbol{\bar v}}}_{n - d + 2}}{\boldsymbol{\bar v}}_{n - d + 2}^{\rm{T}}{{\boldsymbol{R}}_x}} $ (12)步骤3:重复步骤2,直到$d = r$。 -
[1] CAI Haoyuan, KALOORAZI M F, CHEN Jie, et al. Online dominant generalized eigenvectors extraction via a randomized method[C]. 28th European Signal Processing Conference, Amsterdam, Netherlands, 2021: 2353–2357. [2] ZHANG Weitao, LOU Shuntian, and FENG Dazheng. Adaptive quasi-Newton algorithm for source extraction via CCA approach[J]. IEEE Transactions on Neural Networks and Learning Systems, 2014, 25(4): 677–689. doi: 10.1109/TNNLS.2013.2280285 [3] UCHIDA K and YAMADA I. An ℓ1-penalized adaptive normalized quasi-newton algorithm for sparsity-aware generalized Eigen-subspace tracking[J]. Journal of the Franklin Institute, 2020, 357(8): 5033–5057. doi: 10.1016/j.jfranklin.2020.03.034 [4] 沈海鸥, 王布宏, 刘新波. 基于酉变换-矩阵束的稀布线阵方向图综合[J]. 电子与信息学报, 2016, 38(10): 2667–2673.SHEN Haiou, WANG Buhong, and LIU Xinbo. Sparse array pattern synthesis using unitary transformation matrix pencil method[J]. Journal of Electronics &Information Technology, 2016, 38(10): 2667–2673. [5] GAO Yingbin, KONG Xiangyu, ZHANG Zhengxin, et al. An adaptive self-stabilizing algorithm for minor generalized eigenvector extraction and its convergence analysis[J]. IEEE Transactions on Neural Networks and Learning Systems, 2018, 29(10): 4869–4881. doi: 10.1109/TNNLS.2017.2783360 [6] KONG Xiangyu, HU Changhua, and DUAN Zhansheng. Principal Component Analysis Networks and Algorithms[M]. Singapore: Springer, 2017. [7] LIU Lijun, SHAO Hongmei, and NAN Dong. Recurrent neural network model for computing largest and smallest generalized eigenvalue[J]. Neurocomputing, 2008, 71(16/18): 3589–3594. [8] YANG Jian, HU Han, and XI Hongsheng. Weighted non-linear criterion-based adaptive generalised eigendecomposition[J]. IET Signal Processing, 2013, 7(4): 285–295. doi: 10.1049/iet-spr.2012.0212 [9] YANG Jian, XI Hongsheng, YANG Feng, et al. RLS-based adaptive algorithms for generalized Eigen-decomposition[J]. IEEE Transactions on Signal Processing, 2006, 54(4): 1177–1188. doi: 10.1109/TSP.2005.863040 [10] ATTALLAH S and ABED-MERAIM K. A fast adaptive algorithm for the generalized symmetric eigenvalue problem[J]. IEEE Signal Processing Letters, 2008, 15: 797–800. doi: 10.1109/LSP.2008.2006346 [11] TANAKA T. Fast generalized eigenvector tracking based on the power method[J]. IEEE Signal Processing Letters, 2009, 16(11): 969–972. doi: 10.1109/LSP.2009.2027667 [12] NGUYEN T D, TAKAHASHI N, and YAMADA I. An adaptive extraction of generalized eigensubspace by using exact nested orthogonal complement structure[J]. Multidimensional Systems and Signal Processing, 2013, 24(3): 457–483. doi: 10.1007/s11045-012-0172-9 [13] LI Hongzeng, DU Boyang, KONG Xiangyu, et al. A generalized minor component extraction algorithm and its analysis[J]. IEEE Access, 2018, 6: 36771–36779. doi: 10.1109/ACCESS.2018.2852060 [14] 孔祥玉, 冯晓伟, 胡昌华. 广义主成分分析算法及应用[M]. 北京: 国防工业出版社, 2018.KONG Xiangyu, FENG Xiaowei, and HU Changhua. General Principal Component Analysis and Application[M]. Beijing: National Defense Industry Press, 2018. [15] FENG Xiaowei, KONG Xiangyu, DUAN Zhansheng, et al. Adaptive generalized Eigen-pairs extraction algorithms and their convergence analysis[J]. IEEE Transactions on Signal Processing, 2016, 64(11): 2976–2989. doi: 10.1109/TSP.2016.2537260 [16] KUSHNER H J and CLARK D S. Stochastic Approximation Methods for Constrained and Unconstrained Systems[M]. New York: Springer, 1978. [17] NGUYEN T D and YAMADA I. A unified convergence analysis of normalized PAST algorithms for estimating principal and minor components[J]. Signal Processing, 2013, 93(1): 176–184. doi: 10.1016/j.sigpro.2012.07.020 [18] NGUYEN T D and YAMADA I. Necessary and sufficient conditions for convergence of the DDT systems of the Normalized PAST algorithms[J]. Signal Processing, 2014, 94: 288–299. doi: 10.1016/j.sigpro.2013.06.017 [19] O’REGAN G. Matrix theory[M]. O’REGAN G. Guide to Discrete Mathematics: An Accessible Introduction to the History, Theory, Logic and Applications. Cham: Springer, 2016: 127–139. -






 下载:
下载:


 下载:
下载:
