Sparse Autofocus Method for Maneuvering Platform High-squint SAR Based on Two-dimensional Spatial-variant Motion Compensation
-
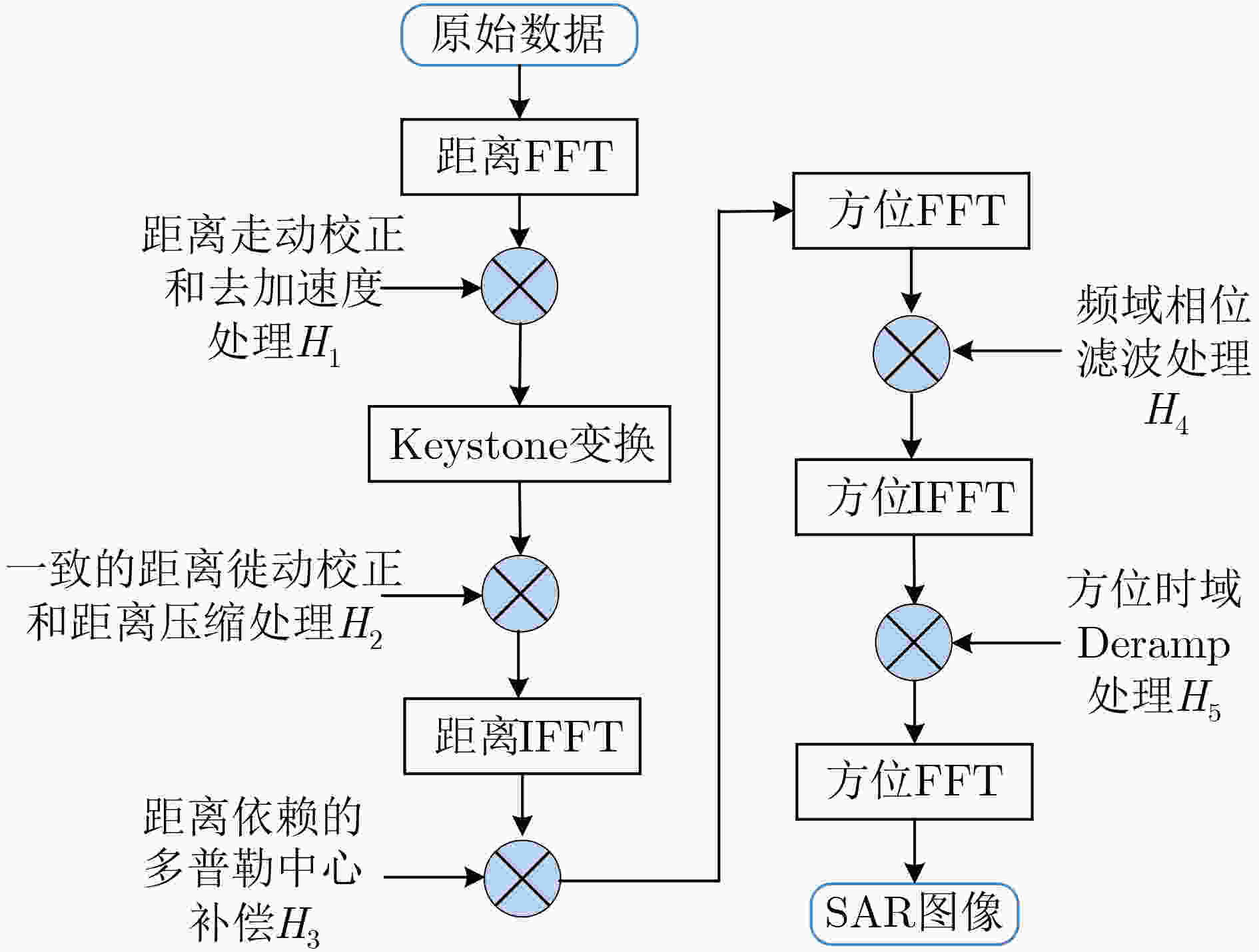
摘要: 大斜视角和空间3维加速度的存在使机动平台SAR的运动误差具有明显的2维空变性,极大地增加了成像难度。为此,该文提出了一种基于2维空变运动误差估计与补偿的稀疏自聚焦方法。该方法基于Keystone变换和频域相位滤波法构造了能够校正成像参数空变性的频域近似观测算子。在自聚焦过程中,首先,构建基于频域近似观测算子的稀疏自聚焦模型并采用迭代软阈值方法(ISTA)进行求解,从而实现图像的粗聚焦和非空变运动误差的估计;然后,采用稀疏自聚焦模型估计多个子区域的精确相位误差曲线,并基于最小二乘法估计空变的运动误差参数;最后,通过对近似观测算子的修正实现空变运动误差的补偿。仿真实验验证了该方法的有效性。Abstract: The existence of high-squint angle and three-dimensional acceleration makes the motion error of maneuvering platform SAR have obvious two-dimensional spatial variability, which greatly increases the difficulty of imaging. A sparse autofocus method based on the estimation and compensation of two-dimensional spatial-variant motion error is proposed. Based on the Keystone transform and the frequency domain phase filtering method, a frequency-domain approximate observation operator is constructed to correct the spatial-variant imaging parameters. In the process of autofocus, firstly, a sparse autofocus model based on the frequency-domain approximate observation operator is constructed to focus the image roughly and estimate the non-spatial-variant motion error parameters, and the Iterative Shrinkage-Thresholding Algorithm (ISTA) is used to solve the constructed sparse autofocus model. Then, the precise phase error curves of multiple sub-regions are obtained by the sparse autofocus model and the least square method can be used to estimate the spatial-variant motion error parameters. Finally, the compensation of spatial-variant motion error is realized by correcting the approximate observation operator. The simulation results show the effectiveness of the proposed method.
-
表 1 仿真参数
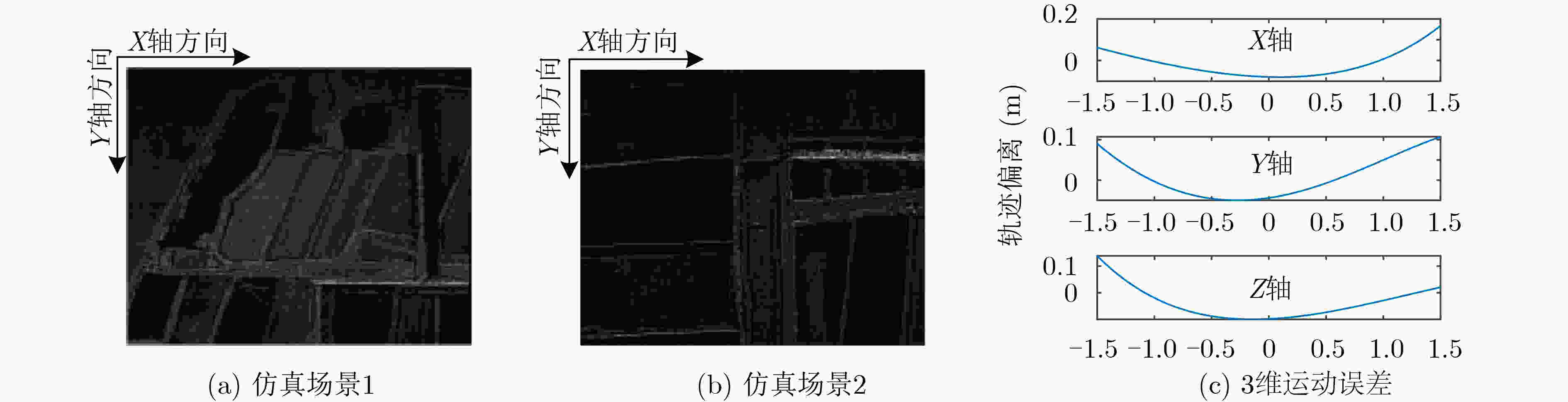
参数 数值 参数 数值 载频 17 GHz 地面斜视角 60° 距离带宽 300 MHz 平台高度 4 km 合成孔径时间 3 s 中心斜距 12 km 脉冲宽度 5 μs 速度 (150, 0, –30) m/s 脉冲重复频率 1 kHz 加速度 (2.2, 1.1, –1.8) m/s2 表 2 场景1成像结果量化分析结果
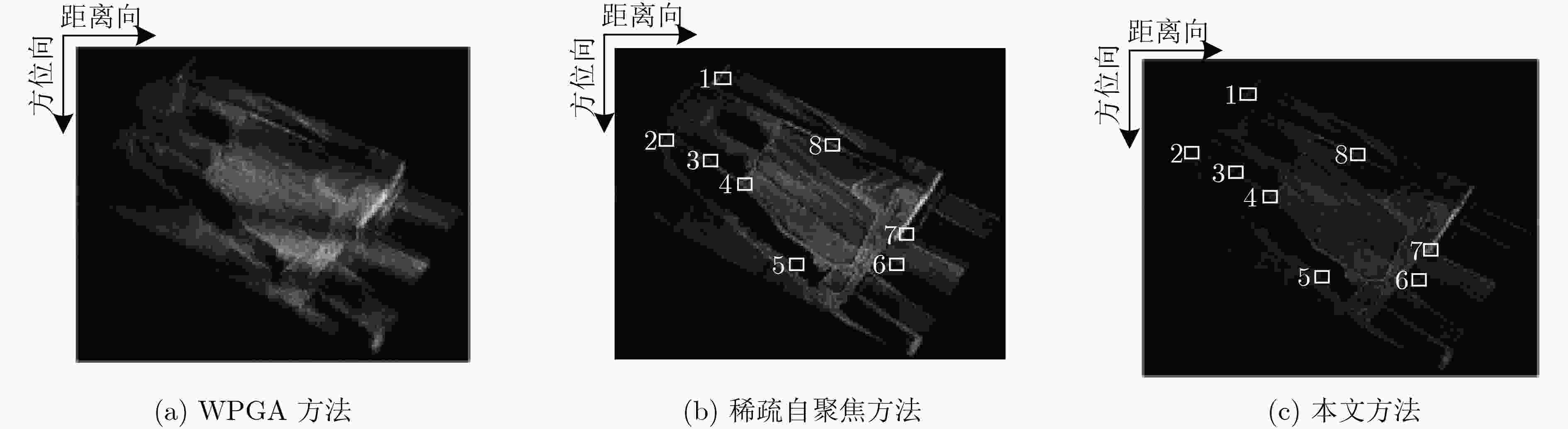
成像方法 熵 对比度 WPGA 14.58 3.95 稀疏自聚焦 14.42 6.82 本文方法 14.31 7.02 -
[1] 李宁, 别博文, 邢孟道, 等. 基于多普勒重采样的恒加速度大斜视SAR成像算法[J]. 电子与信息学报, 2019, 41(12): 2873–2880. doi: 10.11999/JEIT180953LI Ning, BIE Bowen, XING Mengdao, et al. A doppler resampling based imaging algorithm for high squint SAR with constant acceleration[J]. Journal of Electronics &Information Technology, 2019, 41(12): 2873–2880. doi: 10.11999/JEIT180953 [2] HOU Jianqiang, MA Yanheng, and LI Gen. A third-order range separation imaging algorithm for manoeuvring platform SAR[J]. Remote Sensing Letters, 2019, 10(8): 786–795. doi: 10.1080/2150704X.2019.1610982 [3] LI Gen, MA Yanheng, SHI Lin, et al. KT and azimuth sub-region deramp-based high-squint SAR imaging algorithm mounted on manoeuvring platforms[J]. IET Radar, Sonar & Navigation, 2020, 14(3): 388–398. doi: 10.1049/iet-rsn.2019.0251 [4] 李根, 马彦恒, 侯建强, 等. 基于Keystone变换和扰动重采样的机动平台大斜视SAR成像方法[J]. 电子与信息学报, 2020, 42(10): 2485–2492. doi: 10.11999/JEIT190831LI Gen, MA Yanheng, HOU Jianqiang, et al. Maneuvering platform high-squint SAR imaging method based on Keystone transform and perturbation resampling[J]. Journal of Electronics &Information Technology, 2020, 42(10): 2485–2492. doi: 10.11999/JEIT190831 [5] WAHL D E, EICHEL P H, GHIGLIA D C, et al. Phase gradient autofocus-a robust tool for high resolution SAR phase correction[J]. IEEE Transactions on Aerospace and Electronic Systems, 1994, 30(3): 827–835. doi: 10.1109/7.303752 [6] FIENUP J R and MILLER J J. Aberration correction by maximizing generalized sharpness metrics[J]. Journal of the Optical Society of America A, 2003, 20(4): 609–620. doi: 10.1364/JOSAA.20.000609 [7] DE MACEDO K A C, SCHEIBER R, and MOREIRA A. An autofocus approach for residual motion errors with application to airborne repeat-pass SAR interferometry[J]. IEEE Transactions on Geoscience and Remote Sensing, 2008, 46(10): 3151–3162. doi: 10.1109/TGRS.2008.924004 [8] LI Yake and O’YOUNG S. Kalman filter disciplined phase gradient autofocus for stripmap SAR[J]. IEEE Transactions on Geoscience and Remote Sensing, 2020, 58(9): 6298–6308. doi: 10.1109/TGRS.2020.2976655 [9] LIANG Yi, LI Guofei, WEN Jun, et al. A fast time-domain SAR imaging and corresponding autofocus method based on hybrid coordinate system[J]. IEEE Transactions on Geoscience and Remote Sensing, 2019, 57(11): 8627–8640. doi: 10.1109/TGRS.2019.2921917 [10] PU Wei, WU Junjie, HUANG Yulin, et al. Fast factorized backprojection imaging algorithm integrated with motion trajectory estimation for bistatic forward-looking SAR[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2019, 12(10): 3949–3965. doi: 10.1109/JSTARS.2019.2945118 [11] YANG Jungang, HUANG Xiaotao, THOMPSON J, et al. Compressed sensing radar imaging with compensation of observation position error[J]. IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(8): 4608–4620. doi: 10.1109/TGRS.2013.2283054 [12] LI Bo, LIU Falin, ZHOU Chongbin, et al. Phase error correction for approximated observation-based compressed sensing radar imaging[J]. Sensors, 2017, 17(3): 613. doi: 10.3390/s17030613 [13] PU Wei, WU Junjie, WANG Xiaodong, et al. Joint sparsity-based imaging and motion error estimation for BFSAR[J]. IEEE Transactions on Geoscience and Remote Sensing, 2019, 57(3): 1393–1408. doi: 10.1109/TGRS.2018.2866437 [14] ONHON N Ö and CETIN M. A sparsity-driven approach for joint SAR imaging and phase error correction[J]. IEEE Transactions on Image Processing, 2012, 21(4): 2075–2088. doi: 10.1109/TIP.2011.2179056 [15] 李震宇, 梁毅, 邢孟道, 等. 一种大斜视SAR俯冲段频域相位滤波成像算法[J]. 电子学报, 2015, 43(10): 2014–2021. doi: 10.3969/j.issn.0372-2112.2015.10.020LI Zhenyu, LIANG Yi, XING Mengdao, et al. A frequency phase filtering imaging algorithm for high-squint SAR in diving movement[J]. Acta Electronica Sinica, 2015, 43(10): 2014–2021. doi: 10.3969/j.issn.0372-2112.2015.10.020 [16] 别博文, 梁毅, 党彦锋, 等. 曲线轨迹SAR大斜视子孔径成像算法[J]. 系统工程与电子技术, 2017, 39(3): 500–505. doi: 10.3969/j.issn.1001-506X.2017.03.07BIE Bowen, LIANG Yi, DANG Yanfeng, et al. Sub-aperture imaging algorithm for high squint SAR with curvilinear flight tracks[J]. Systems Engineering and Electronics, 2017, 39(3): 500–505. doi: 10.3969/j.issn.1001-506X.2017.03.07 [17] 李根, 马彦恒, 侯建强, 等. 基于子孔径Keystone变换的曲线轨迹大斜视SAR回波模拟[J]. 电子与信息学报, 2020, 42(9): 2261–2268. doi: 10.11999/JEIT190674LI Gen, MA Yanheng, HOU Jianqiang, et al. Sub-aperture Keystone transform based echo simulation method for high-squint SAR with a curve trajectory[J]. Journal of Electronics &Information Technology, 2020, 42(9): 2261–2268. doi: 10.11999/JEIT190674 -





 下载:
下载:





 下载:
下载:
