Low-complexity Early Stopping Criterion for Belief Propagation Decoding of Polar Codes
-
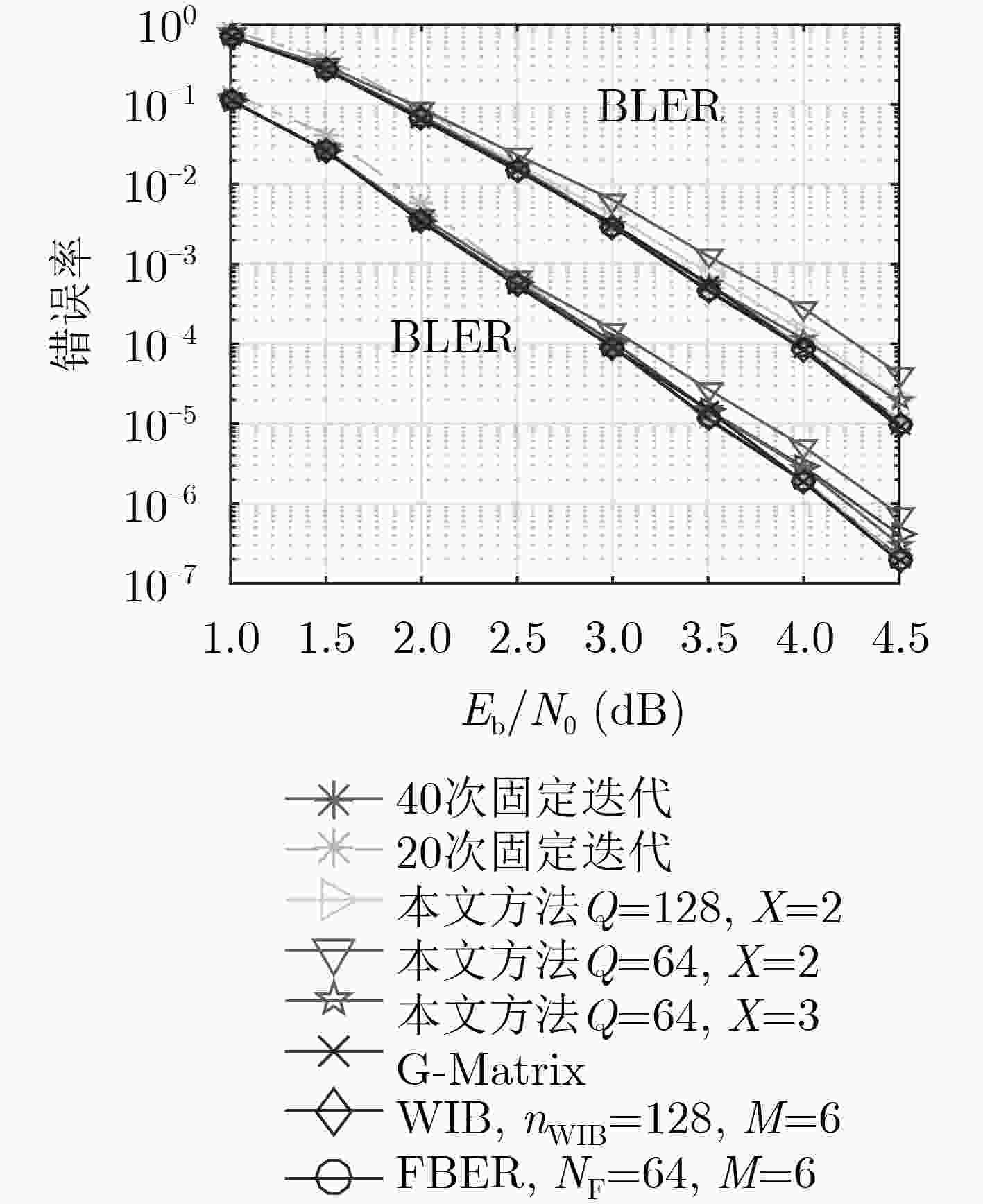
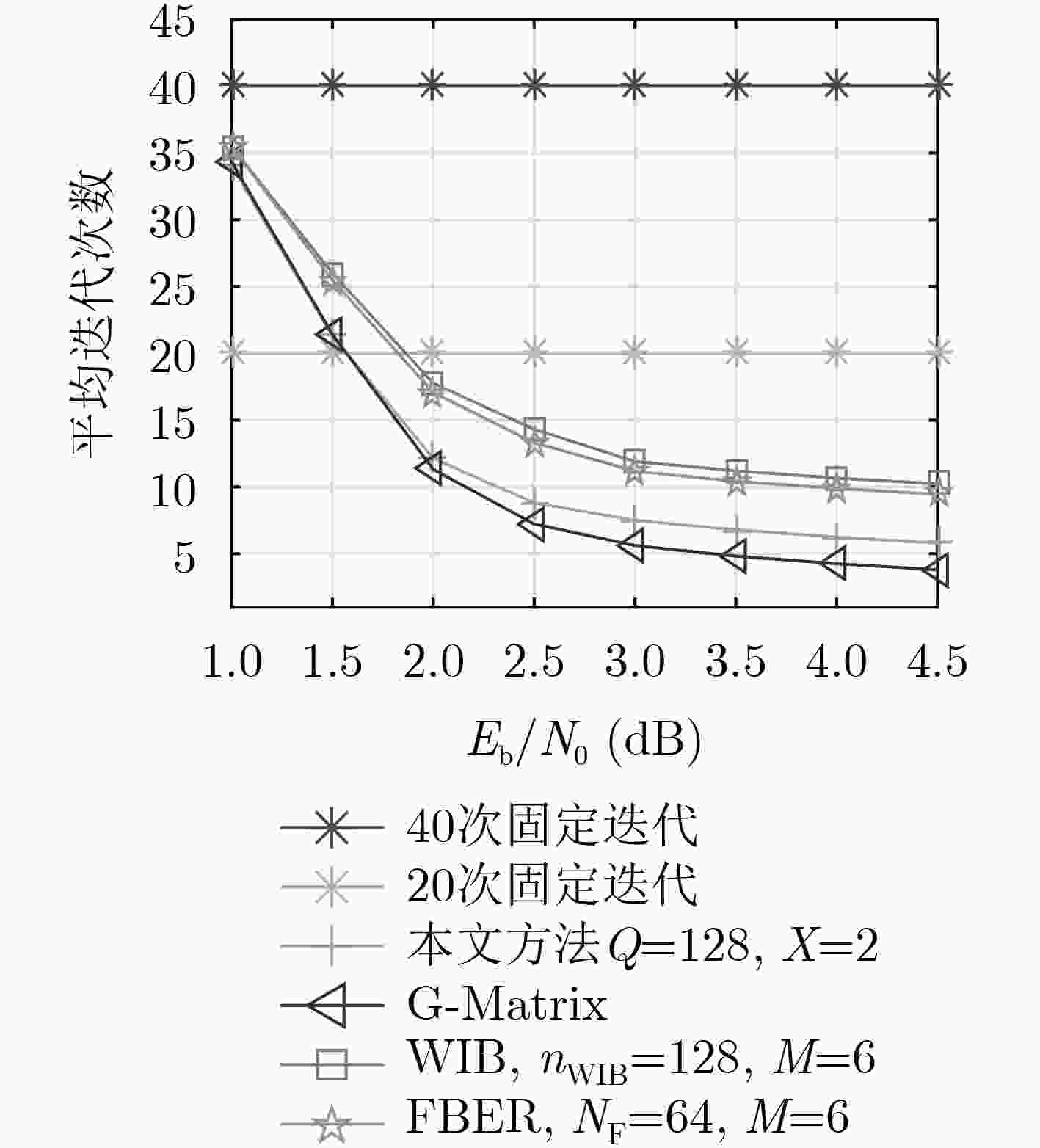
摘要: 针对极化码译码延迟较高的问题, 该文提出了一种针对置信度传播算法的早期停止准则,通过监测码字估值
$\hat x$ 的收敛性来终止译码。该准则利用高斯近似分析选取码字中Q个出错概率较小的比特构成比较空间,由于比较的位数较少,且仅采用异或和或运算,其计算复杂度较低。与基于信息序列估值$\hat u$ 的方案不同,提出的准则在计算$\hat u$ 之前已完成检测,不会导致额外的译码延迟。仿真和FPGA综合结果表明: 该准则相对于G-Matrix, 最坏信息位(WIB)和冻结位误码率(FBER)可有效节省硬件资源;当最大迭代次数设置为40次时,相比于G-Matrix准则,复杂度下降的代价是平均迭代次数在3.5 dB处上升了29.98%,相比于WIB和FBER方案,平均迭代次数分别减少39.44%和27.67%。Abstract: Considering the high decoding latency of polar code, an early stopping criterion for belief propagation is presented, which terminates the decoding by monitoring the convergence of codeword estimate$\hat x$ . In this paper, Gaussian approximation is used to analyze and select Q bit with low error probability to construct the comparison space. Because the number of bit to be compared is small and only XOR and OR operation is used, the computational complexity is low. Different from other criteria based on$\hat u$ , the proposed criterion does not lead to additional latency for it has been completed before calculating$\hat u$ . Simulation and FPGA Synthesis results show that compared with G-matrix, Worst Information Bit (WIB) and Frozen Bit Error Rate (FBER), this criterion can effectively save hardware resource.When the maximum iteration number is set to 40, compared with the G-matrix criterion, the average iteration time is increased by 29.98% at 3.5 dB, and the average iteration times are reduced by 39.44% and 27.67% respectively compared with the WIB and FBER schemes.-
Key words:
- Polar code /
- Belief propagation /
- Early stopping criterion /
- Low-complexity /
- Codeword estimate
-
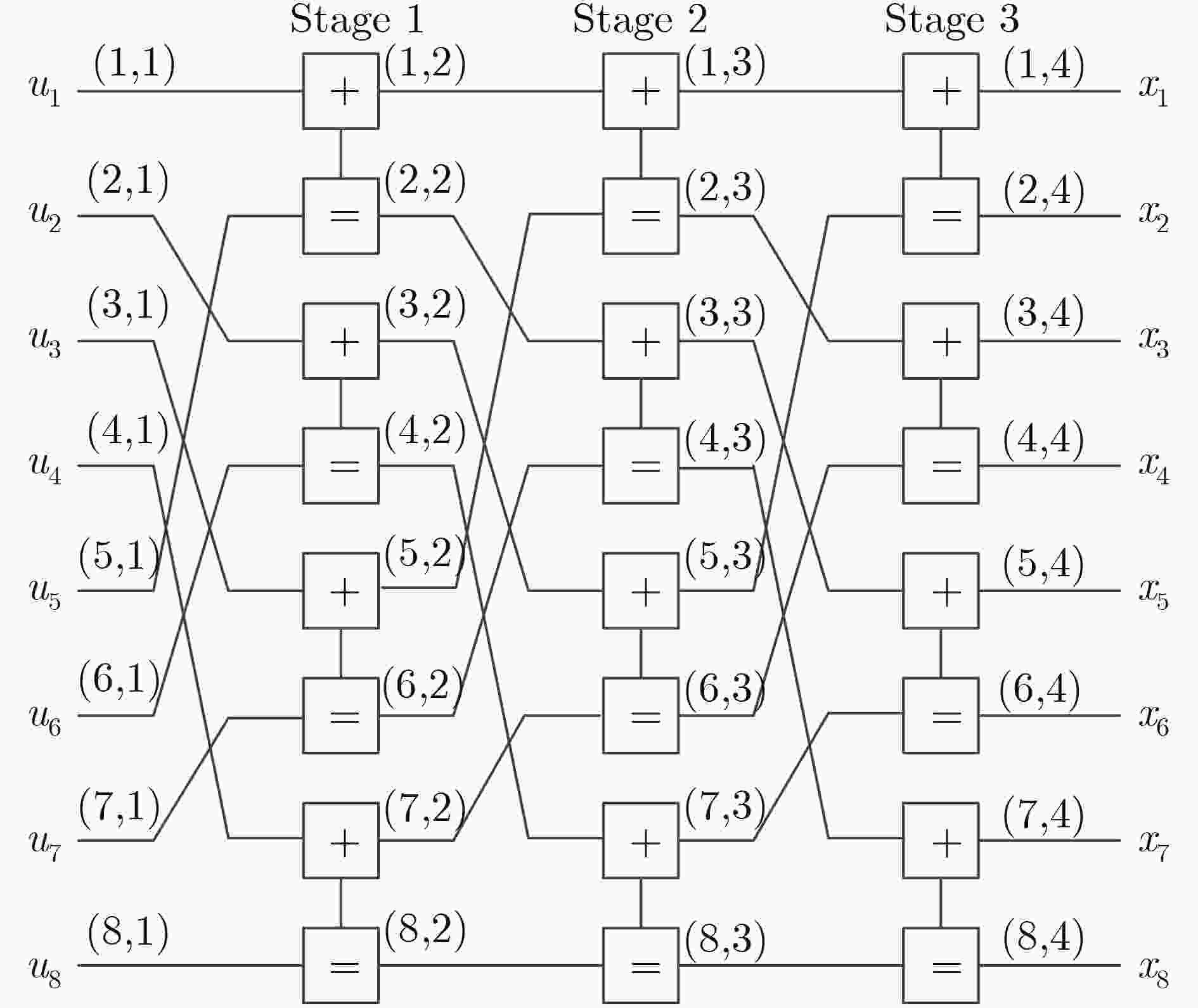
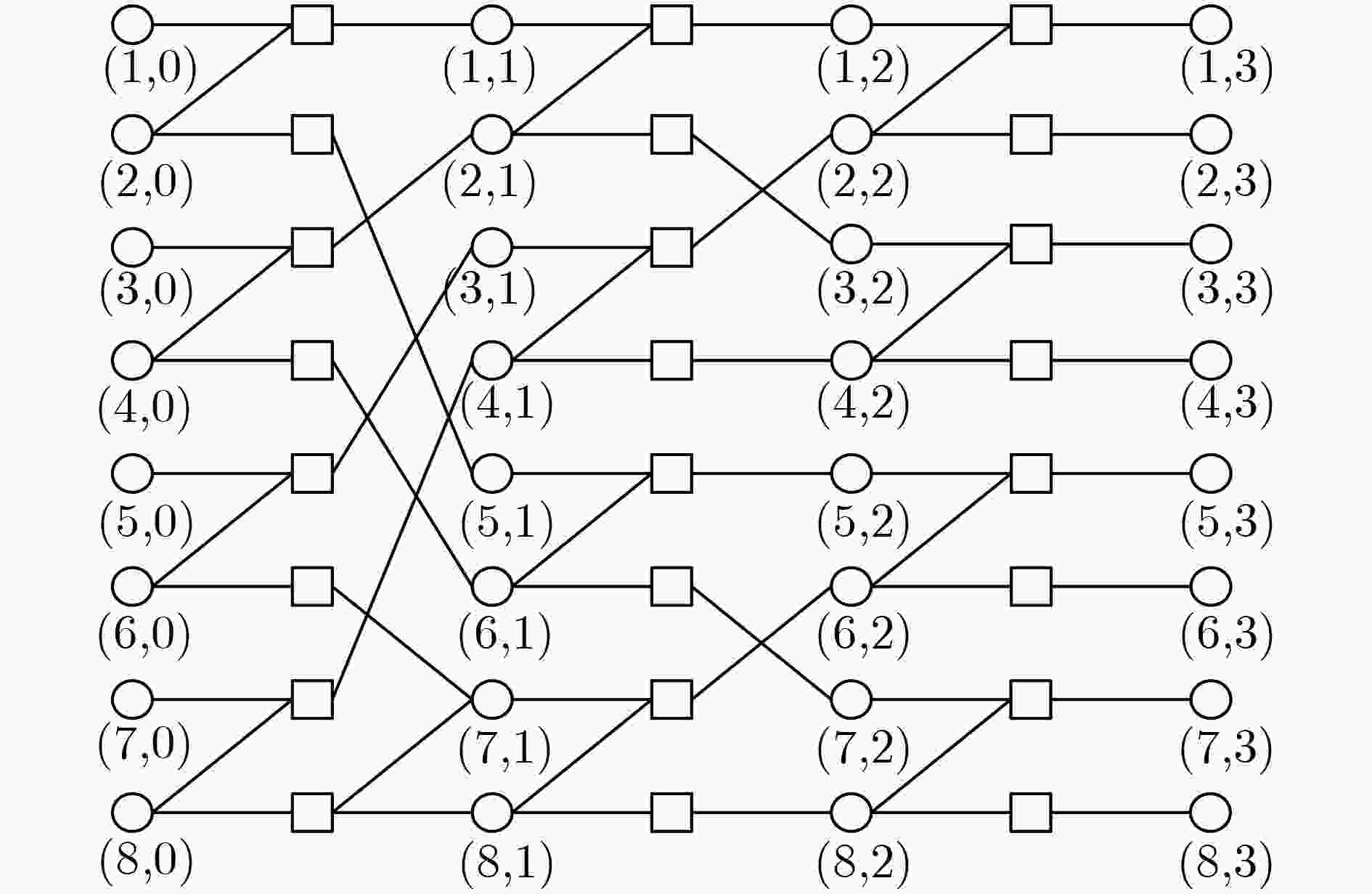
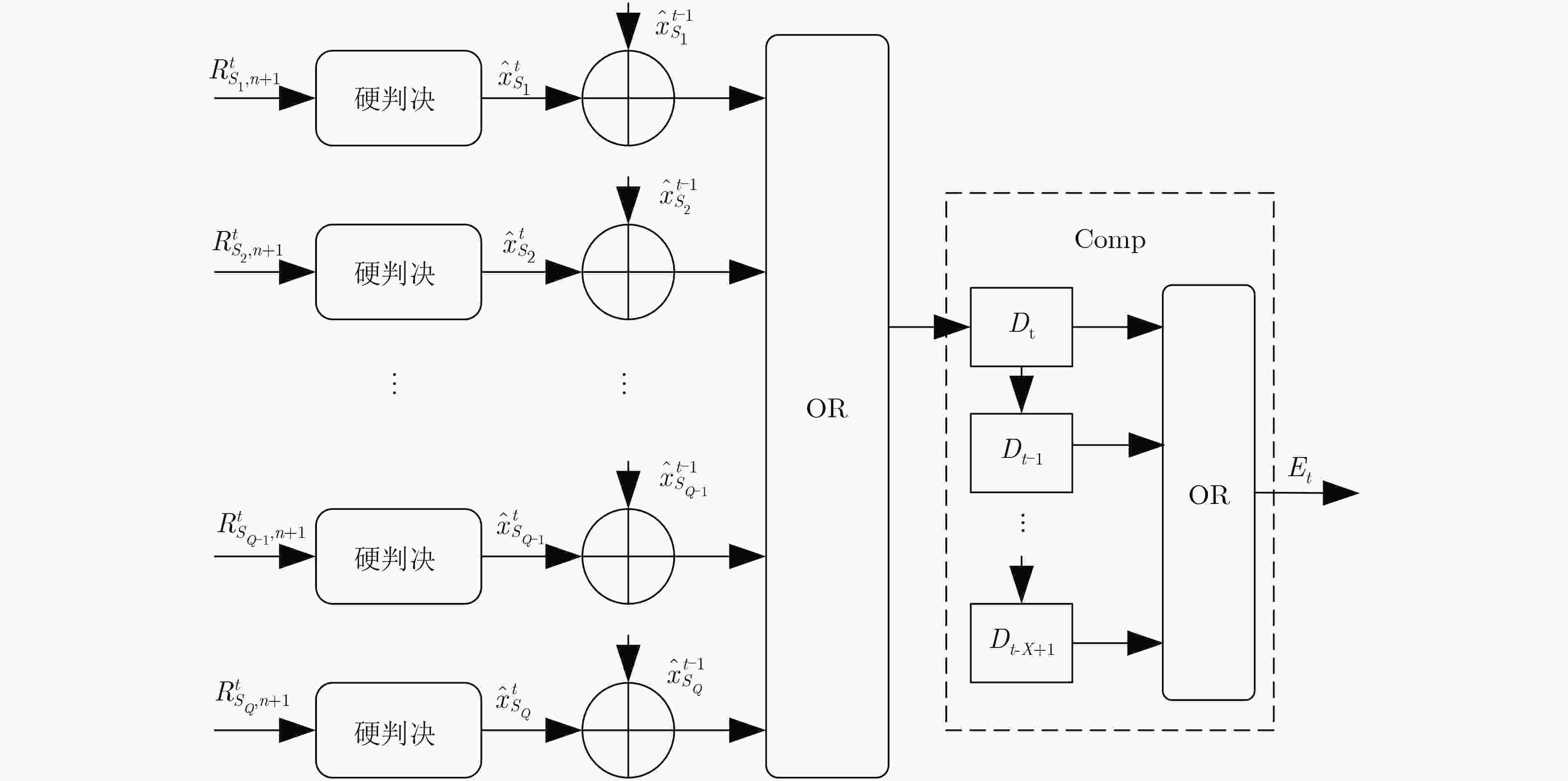
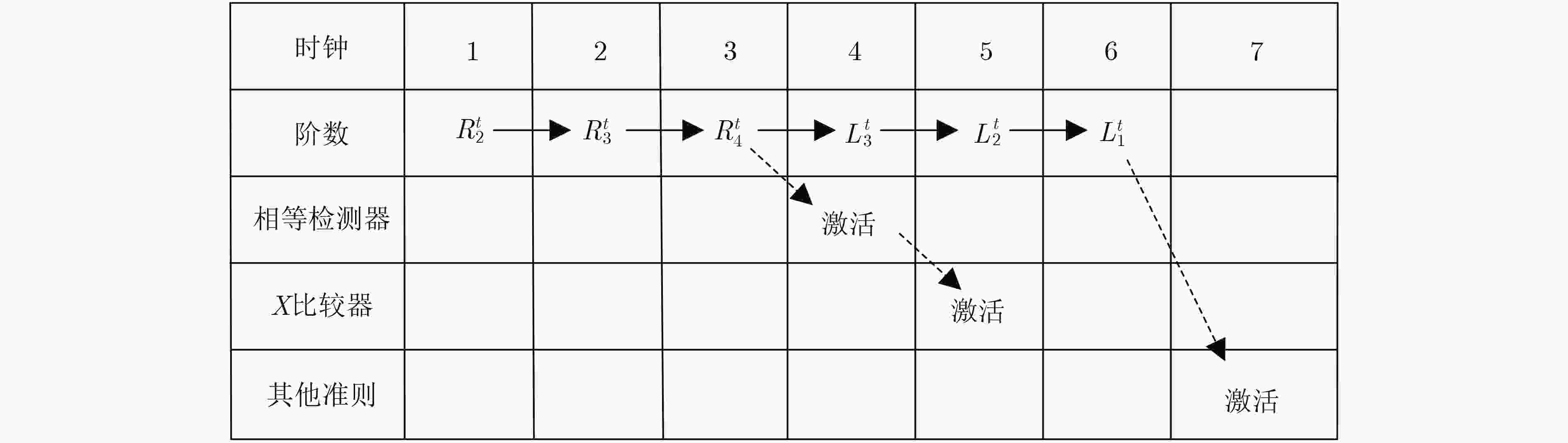
算法1 (N, K) X-tolerance BP译码器 (1) 输入: (2) 信道输出:${\rm{ LLR}}\left( { {r_i} } \right)$ (3) 冻结位集合:$ A^C$ (4) 比较空间:S (5) 初始化: (6) 设定$ {I_{\max }}$和X (7) For 每个节点的传播信息$ L_{i,j}^t$和$ R_{i,j}^t$ (8) if $ (j = = 1)$ & $ \left( {i \in {A^C}} \right)$ $ R_{i,1}^t = \infty $对于t=0, 1,···, Imax (9) else if $ (j = = 1 + n)$ $L_{i,n + 1}^t = {\rm{LLR}}\left( { {r_i} } \right)$对于t=0, 1,···,
Imax x(10) else $ L_{i,j}^0 = R_{i,j}^0 = 0$ (11) 迭代过程: (12) While $ t < {I_{\max }}$ do (13) 根据(1)更新每个节点的$ L_{i,j}^t$ and $ R_{i,j}^t$ (14) 更新 $ \hat x_1^N$ (15) if $ R_{i,n + 1}^t > 0$ then $ {{\hat x}_i} = 0$ (16) else $ {{\hat x}_i} = 1$ (17) end while (18) 提前停止准则: (19) if (17) 成立 then (20) 迭代终止 (21) else $ t=t+1$ (22) 输出:$ \hat u_1^N = \left( {{{\hat u}_1},{{\hat u}_2}, ··· ,{{\hat u}_N}} \right)$ 表 1 早期停止准则的计算复杂度比较
停止准则 G-Matrix WIB FBER X-tolerance Q=N/8 Q=N/16 加法运算 2N M+2N/8 M+N/16 – – 比较运算 3N – – – 1 异或(XOR) NlogN N/8 N/16 N/8 N/16 或(OR) – – X+N/8 X+N/16 表 2 不同早期停止准则的综合结果
停止准则 G-Matrix WIB FBER X-tolerance Q=128 X=2 Q=64 X=3 ALMs 30265 1820 1260 50 27 Registers 3073 330 210 131 68 -
https://www.oulu.fi/university/news/6g-white-paper, 2019. ARIKAN E. Channel polarization: A method for constructing capacity-achieving codes for symmetric binary-input memoryless channels[J]. IEEE Transactions on Information Theory, 2009, 55(7): 3051–3071. doi: 10.1109/TIT.2009.2021379 刘建航, 何怡静, 李世宝, 等. 基于预译码的极化码最大似然简化连续消除译码算法[J]. 电子与信息学报, 2019, 41(4): 959–966. doi: 10.11999/JEIT180324LIU Jianhang, HE Jingyi, LI Shibao, et al. Pre-decoding based maximum-likelihood simplified successive-cancellation decoding of polar codes[J]. Journal of Electronics &Information Technology, 2019, 41(4): 959–966. doi: 10.11999/JEIT180324 郭锐, 王美洁, 王杰. 基于缩短极化码的MLC NAND Flash差错控制技术研究[J]. 电子与信息学报, 2017, 39(7): 1658–1665. doi: 10.11999/JEIT160864GUO Rui, WANG Meijie, and WANG Jie. Research on the MLC Nand flash error control technology based on polar codes[J]. Journal of Electronics &Information Technology, 2017, 39(7): 1658–1665. doi: 10.11999/JEIT160864 LAY K T and CHANG C H. Enhanced successive cancellation for decoding of polar codes with very low latency through multiple parity checks[C]. The 4th International Conference on Intelligent Green Building and Smart Grid, Yichang, China, 2019: 366–370. doi: 10.1109/IGBSG.2019.8886186. YUAN Bo and PARHI K K. Early stopping criteria for energy-efficient low-latency belief-propagation polar code decoders[J]. IEEE Transactions on Signal Processing, 2014, 62(24): 6496–6506. doi: 10.1109/tsp.2014.2366712 YAN Yongli, ZHANG Xuanxuan, and WU Bin. Simplified early stopping criterion for belief-propagation polar code decoder based on frozen bits[J]. IEEE Access, 2019, 7: 134691–134696. doi: 10.1109/ACCESS.2019.2940135 CHOI S and YOO H. Area-efficient early-termination technique for belief-propagation polar decoders[J]. Electronics, 2019, 8(9): 1001. doi: 10.3390/electronics8091001 REN Yuanrui, ZHANG Chuan, LIU Xing, et al. Efficient early termination schemes for belief-propagation decoding of polar codes[C]. The 11th IEEE International Conference on ASIC, Chengdu, China, 2015: 1–4. doi: 10.1109/ASICON.2015.7517046. SIMSEK C and TURK K. Simplified early stopping criterion for belief-propagation polar code decoders[J]. IEEE Communications Letters, 2016, 20(8): 1515–1518. doi: 10.1109/LCOMM.2016.2580514 SIMSEK C and TURK K. Hardware optimization for belief propagation polar code decoder with early stopping criteria using high-speed parallel-prefix ling adder[C]. The 40th International Conference on Telecommunications and Signal Processing, Barcelona, Spain, 2017: 182–185. doi: 10.1109/TSP.2017.8075964. ALBAYRAK C, SIMSEK C, and TURK K. Low-complexity early termination method for rateless soft decoder[J]. IEEE Communications Letters, 2017, 21(11): 2356–2359. doi: 10.1109/LCOMM.2017.2740207 ZHANG Qingshuang, LIU Aijun, and TONG Xinhai. Early stopping criterion for belief propagation polar decoder based on frozen bits[J]. Electronics Letters, 2017, 53(24): 1576–1578. doi: 10.1049/el.2017.3316 GIARD P, BALATSOUKAS-STIMMING A, and BURG A. On the tradeoff between accuracy and complexity in blind detection of polar codes[C]. The 10th IEEE International Symposium on Turbo Codes & Iterative Information Processing, Hongkong, China, 2018: 1–5. doi: 10.1109/ISTC.2018.8625366. CHUNG S Y, RICHARDSON T J, and URBANKE R L. Analysis of sum-product decoding of low-density parity-check codes using a Gaussian approximation[J]. IEEE Transactions on Information Theory, 2001, 47(2): 657–670. doi: 10.1109/18.910580 梁昌洪, 李龙, 史小卫. 标准正态分布的简洁闭式[J]. 西安电子科技大学学报: 自然科学版, 2003, 30(3): 289–292. doi: 10.3969/j.issn.1001-2400.2003.03.001LIANG Changhong, LI Long, and SHI Xiaowei. A compact closed form of standard normal distribution[J]. Journal of Xidian University, 2003, 30(3): 289–292. doi: 10.3969/j.issn.1001-2400.2003.03.001 -









 下载:
下载:







 下载:
下载:
