Edge Spreading Optimization for Terminated Protograph-based Low-Density Parity-Check Convolutional Codes
-
摘要: 截断式原模图低密度奇偶校验(LDPC)卷积码(P-LDPC-CCs)结合了原模图LDPC (P-LDPC)码和卷积码的特点,具有多变的编码构造方式和优异的纠错性能,实现了编译码低时延特性。边扩展作为构造截断式原模图LDPC卷积码基础矩阵关键步骤,是影响其性能的重要因素。该文提出了一种边扩展优化方法。该方法利用原模图外信息转移(P-EXIT)算法理论分析基础矩阵的译码门限,引入差分进化思想搜索一定条件下最优的边扩展方式。理论分析与系统仿真结果均表明所提边扩展优化方法比现有的方法具有更好的性能。
-
关键词:
- 截断式原模图低密度奇偶校验卷积码 /
- 原模图外信息转移 /
- 边扩展 /
- 优化
Abstract: Terminated Protograph-based Low-Density Parity-Check (LDPC) Convolutional Codes (Terminated P-LDPC-CCs), which combine the characteristics of Protograph-based LDPC (P-LDPC) codes and convolutional codes, have variable encoding constructed schemes, excellent error-correcting performance, and high-speed coding characteristics. As the key step of constructing Terminated P-LDPC-CCs, edge spreading is an important factor to determine the performance. In this paper, an edge spreading optimization method is proposed. In the proposed method, the differential evolution algorithm is introduced to search the best edge spreading mode based on the decoding threshold calculated by Protograph-based EXtrinsic Information Transfer (P-EXIT) analysis. Both P-EXIT analysis and simulation results indicate that the proposed edge spreading optimization method can achieve better performance. -
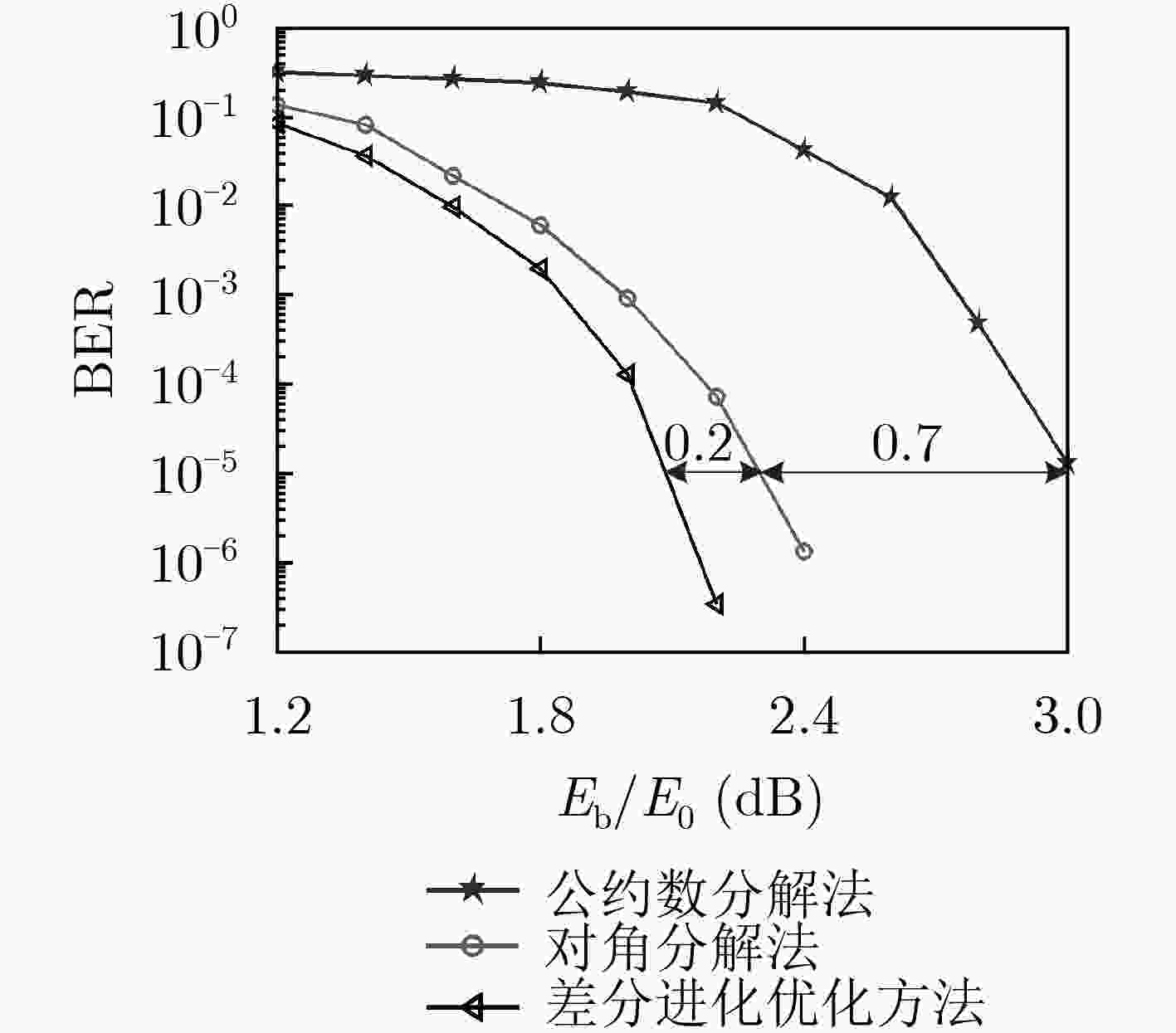
表 1 R4JA码不同边扩展方法在L = 3的基础矩阵的译码门限(dB)
边扩展方法 公约数分解法 对角分解法 差分进化优化方法 译码门限 2.010 1.070 0.905 表 2 R4JA码构造截断式原模图LDPC卷积码参数
边扩展方法 差分进化优化方法、公约数分解法、对角分解法 原模图 1/2码率R4JA码 记忆长度 1 终止因子L 3 码率R 1/3 信源码长 6000 是否删余 否 表 3 AR4JA码不同边扩展方法在L = 3的基础矩阵的译码门限(dB)
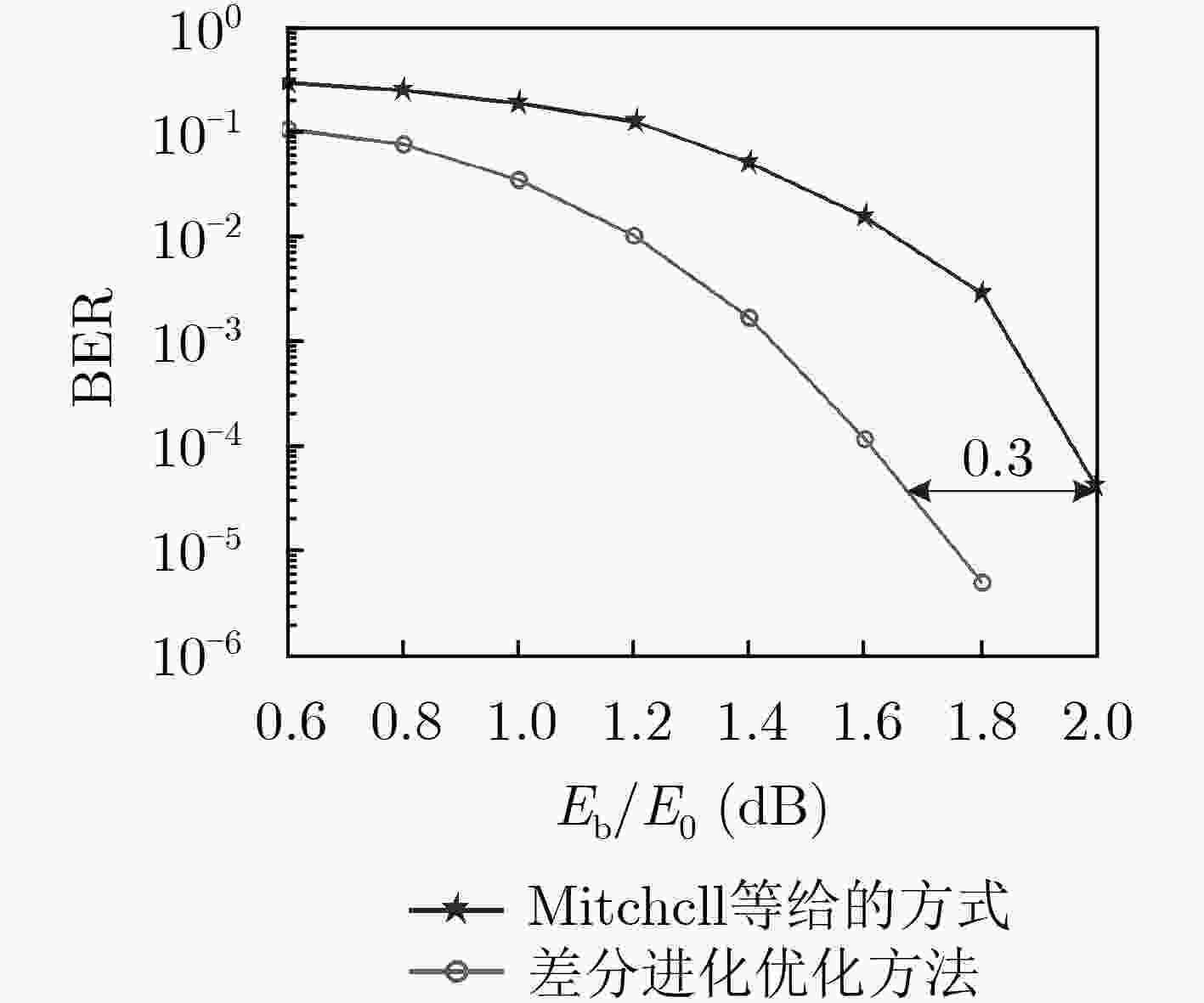
边扩展方法 Mitchell等给的方式 差分进化优化方法 译码门限 0.594 0.410 表 4 AR4JA码构造截断式原模图LDPC卷积码参数
边扩展方法 差分进化优化方法、Mitchell等给的方式 原模图 1/2码率AR4JA码 记忆长度 1 终止因子L 3 码率R 1/3 信源码长 2000 是否删余 是 表 5 AR4JA码在不同截断因子L的基础矩阵的译码门限 (dB)
L 码率R 差分进化优化方法 Mitchell等给的方式 差值 2 1/4 0.377 0.651 0.274 3 1/3 0.410 0.594 0.184 4 3/8 0.551 0.617 0.066 5 2/5 0.596 0.632 0.036 6 5/12 0.614 0.636 0.022 7 3/7 0.616 0.629 0.013 -
GIORDANI M, POLESE M, MEZZAVILLA M, et al. Toward 6G networks: Use cases and technologies[J]. IEEE Communications Magazine, 2020, 58(3): 55–61. doi: 10.1109/MCOM.001.1900411 TOMKOS I, KLONIDIS D, PIKASIS E, et al. Toward the 6G network Era: Opportunities and challenges[J]. IT Professional, 2020, 22(1): 34–38. doi: 10.1109/MITP.2019.2963491 MITCHELL D G M, LENTMAIER M, and COSTELLO D J. New families of LDPC block codes formed by terminating irregular protograph-based LDPC convolutional codes[C]. 2010 IEEE International Symposium on Information Theory, Austin, USA, 2010: 824–828. doi: 10.1109/ISIT.2010.5513633. MITCHELL D G M, PUSANE A E, ZIGANGIROV K S, et al. Asymptotically good LDPC convolutional codes based on protographs[C]. 2008 IEEE International Symposium on Information Theory, Toronto, Canada, 2008: 1030–1034. doi: 10.1109/ISIT.2008.4595143. LENTMAIER M and FETTWEIS G P. On the thresholds of generalized LDPC convolutional codes based on protographs[C]. 2010 IEEE International Symposium on Information Theory, Austin, USA, 2010: 709–713. doi: 10.1109/ISIT.2010.5513595. PAPALEO M, IYENGAR A R, SIEGEL P H, et al. Windowed erasure decoding of LDPC convolutional codes[C]. 2010 IEEE Information Theory Workshop on Information Theory, Cairo, Egypt, 2010: 1–5. doi: 10.1109/ITWKSPS.2010.5503166. IYENGAR A R, PAPALEO M, SIEGEL P H, et al. Windowed decoding of protograph-based LDPC convolutional codes over erasure channels[J]. IEEE Transactions on Information Theory, 2012, 58(4): 2303–2320. doi: 10.1109/TIT.2011.2177439 ALI I, KIM J H, KIM S H, et al. Improving windowed decoding of SC LDPC codes by effective decoding termination, message reuse, and amplification[J]. IEEE Access, 2018, 6: 9336–9346. doi: 10.1109/ACCESS.2017.2771375 吴皓威, 武小飞, 邹润秋, 等. 空间耦合LDPC码的分层译码算法[J]. 电子与信息学报, 2020, 42(8): 1881–1887. doi: 10.11999/JEIT190626WU Haowei, WU Xiaofei, ZOU Runqiu, et al. A layered decoding algorithm for spatially-coupled LDPC codes[J]. Journal of Electronics &Information Technology, 2020, 42(8): 1881–1887. doi: 10.11999/JEIT190626 张娅妹, 周林, 陈辰, 等. 窗口可变的空间耦合LDPC码滑窗译码算法[J]. 西安电子科技大学学报, 2020, 47(3): 128–134. doi: 10.19665/j.issn1001-2400.2020.03.018ZHANG Yamei, ZHOU Lin, CHEN Chen, et al. Sliding window decoding algorithm for spatially coupled LDPC codes with a variable window[J]. Journal of Xidian University, 2020, 47(3): 128–134. doi: 10.19665/j.issn1001-2400.2020.03.018 MITCHELL D G M, LENTMAIER M, and COSTELLO D J. Spatially coupled LDPC codes constructed from protographs[J]. IEEE Transactions on Information Theory, 2015, 61(9): 4866–4889. doi: 10.1109/TIT.2015.2453267 MITCHELL D G M, PUSANE A E, and COSTELLO D J. Minimum distance and trapping set analysis of protograph-based LDPC convolutional codes[J]. IEEE Transactions on Information Theory, 2013, 59(1): 254–281. doi: 10.1109/TIT.2012.2211995 LENTMAIER M, MITCHELL D G M, FETTWEIS G P, et al. Asymptotically regular LDPC codes with linear distance growth and thresholds close to capacity[C]. 2010 Information Theory and Applications Workshop, San Diego, USA, 2010: 1–8. doi: 10.1109/ITA.2010.5454141. 房明. LDPC码构造方法和编码算法研究[D]. [硕士论文], 北京邮电大学, 2014. 余鑫沅. 终止的原模图LDPC卷积码的性能分析和优化[D]. [硕士论文], 厦门大学, 2017.YU Xinyuan. The performance analysis and optimization of terminated protograph-based LDPC convolutional codes[D]. [Master dissertation], Xiamen University, 2017. JIMENEZ FELSTROM A and ZIGANGIROV K S. Time-varying periodic convolutional codes with low-density parity-check matrix[J]. IEEE Transactions on Information Theory, 1999, 45(6): 2181–2191. doi: 10.1109/18.782171 DAS S and SUGANTHAN P N. Differential evolution: A survey of the state-of-the-art[J]. IEEE Transactions on Evolutionary Computation, 2011, 15(1): 4–31. doi: 10.1109/TEVC.2010.2059031 CHEN Qiwang, WANG Lin, HONG Shaohua, et al. Integrated design of JSCC scheme based on double protograph LDPC codes system[J]. IEEE Communications Letters, 2019, 23(2): 218–221. doi: 10.1109/LCOMM.2018.2890243 CHEN Qiwang, HONG Shaohua, and CHEN Yifan. Design of linking matrix in JSCC scheme based on double protograph LDPC codes[J]. IEEE Access, 2019, 7: 92176–92183. doi: 10.1109/ACCESS.2019.2927864 LIU Sanya, CHEN Chen, WANG Lin, et al. Edge connection optimization for JSCC system based on DP-LDPC codes[J]. IEEE Wireless Communications Letters, 2019, 8(4): 996–999. doi: 10.1109/LWC.2019.2903442 -





 下载:
下载:


 下载:
下载:
