非平稳信道下的鲁棒数据链优化设计综述——带限环境下的混沌传输系统

苗美媛; 宋丹; 徐位凯; 湛佳; 王琳

doi:10.11999/JEIT200311

非平稳信道下的鲁棒数据链优化设计综述——带限环境下的混沌传输系统

doi: 10.11999/JEIT200311

苗美媛¹,
宋丹¹,
徐位凯¹,
湛佳²,
王琳^1, ,

1.
厦门大学信息学院厦门 361005
2.
香港理工大学电子与信息工程学院香港 999077

基金项目: 国家自然科学基金(61671395, 61871337)

详细信息

作者简介:
苗美媛：女，1991年生，博士生，研究方向为混沌调制，带限传输系统

宋丹：女，1994年生，博士生，研究方向为联合信源信道编码

徐位凯：男，1976年生，副教授，研究方向为超宽带与混沌通信

湛佳：女，1991年生，博士生，研究方向为联合信源信道编码

王琳：男，1963年生，教授，博士生导师，研究方向为信息论与编码，数字通信理论

通讯作者:
王琳　wanglin@xmu.edu.cn

中图分类号: TN911.3
计量
- 文章访问数: 1799
- HTML全文浏览量: 627
- PDF下载量: 163
- 被引次数: 0
出版历程
- 收稿日期: 2020-04-27
- 修回日期: 2020-07-08
- 网络出版日期: 2020-07-22
- 刊出日期: 2021-01-15

Survey of Optimization Design for Robust Data Link over Non-stationary Channels-chaotic Transmission Systems over Band-limited Environments

1.
College of Information, Xiamen University, Xiamen 361005, China
2.
Department of Electronics and Information Engineering, Hong Kong Polytechnic University, Hongkong 999077, China

Funds: The National Natural Science Foundation of China (61671395, 61871337)

摘要

摘要: 近年来，以物联网(IoT)为基础的6G的相关技术研究引起了研究单位、高校和工业界的广泛关注，其中还有一些重要的问题亟待解决。如何以较低的成本保证带限非平稳环境下数据传输的鲁棒性是一个非常重要的问题。该文介绍了一种低复杂度、低功耗的调制解调传输技术，即差分混沌键控(DCSK)调制。该文将分别描述和分析该系统在标准和非标准传输环境下的特性、优势及其改进方法。同时将提供一些基于多元DCSK(MDCSK)的新型编码调制方案来提高系统在带限环境下的传输质量，这将有助于在低功耗、低成本的网络上，特别是在非平稳信道上提升系统的鲁棒性。结果表明这些优化工作显著地改善了系统性能。之后针对非平稳信道特性系统参数的优化与自适应传输机制将成为未来研究的热点。
- 差分混沌键控 /
- 非平稳信道 /
- 编码调制
Abstract: Recently 6G based on Internet of Things (IoT) is attracted much attention from research units, universities and industries. There are some important problems leaved for us to resolve. One of the most important problems is how to keep robust transmitting through band-limited non-stationary channels with low cost. In this overview, one low complexity, low power consumption modulation and demodulation transmitting technique, namely, Differential Chaos Shift Keying (DCSK) with its modified ways, is introduced in wireless and wired transmission environment. Their properties and advantages of the models under traditional and non-standard transmission environments are described and analyzed. Meanwhile some new coded M-ary Differential Chaos Shift Keying (MDCSK) schemes to enhance their quality of the system transmitting over band-limited transmission environments are provided, which are beneficial to improve the robust transmitting over networks with low power consumption and low cost, particularly, over non-stationary channels. The results show that the optimization work improves the system performance significantly. After that, the optimization and adaptive mechanics of the system parameters for the non-stationary channel characteristics will become a future research hotspot.
- Differential Chaos Shift Keying (DCSK) /
- Non-stationary channel /
- Coded modulation

HTML全文

图 1 MDCSK的系统框图

下载: 全尺寸图片幻灯片

图 2 MDCSK和MPSK-DCSK在扩频因子β=60，M=2, 4, 8, 16, 32的误码率性能曲线

下载: 全尺寸图片幻灯片

图 3 一般化MR-8元DCSK星座及其灰编码映射与判决边界

下载: 全尺寸图片幻灯片

图 4 AWGN信道下，2/4/8/16-DCSK系统的BER性能

下载: 全尺寸图片幻灯片

图 5 方形星座图与判决边界

下载: 全尺寸图片幻灯片

图 6 多径Rayleigh衰落信道下不同系统的误码率

下载: 全尺寸图片幻灯片

图 7 不同信道下误码率比较

下载: 全尺寸图片幻灯片

图 8 码率1/2的ARJA-16-DC-BICM与方形的4-DCSK的误码率性能比较

下载: 全尺寸图片幻灯片

图 9 BICM DS/SS-5 DC-BICM系统误码率比较

下载: 全尺寸图片幻灯片

图 10 多径PLC信道下BER性能比较

下载: 全尺寸图片幻灯片

图 11 PLC中误码率比较

下载: 全尺寸图片幻灯片

图 12 时变UWA信道3个通道场景及脉冲响应

下载: 全尺寸图片幻灯片

图 13 不同UWA信道下MC-CS-DCSK,OFDM-CS-DCSK和MM-DCSK的误码率性能比较

下载: 全尺寸图片幻灯片

表 1 EXIT码型搜索算法流程

初始化：
设定预先设定信息比特GPs g₁,g_2,···,g_m,
设定 G_r={所有可能的g_r}, SNR, k, $\varGamma = \{ \phi \}$
程序：
(1) G_r选择一个新的g_r
(2)当SNR=$\gamma $时，计算选择的GPs的EXIT曲线
(3) 如果通道打开，则令SNR=SNR-k，并且执行第(2)步；如果通道关闭，则在$\Gamma $中保存$\gamma + k/2$作为当前选定的GPs的预测阈值，并执行　　第(4)步
(4) 如果在GPs中有未测试的元素，则返回第(2)步，否则执行第(5)步
(5) 搜索最小值并保存到$\varGamma$中，其对应的GPs这是我们要寻找的好的码型结构

下载: 导出CSV

表 2 多径PLC信道参数

路径编号	信道增益	延时(τ(T_c))
1	0.3645–0.4860i	0
2	0.3037+0.4252i	2
3	0.1822–0.3645i	5
4	0.3645–0.2430i	1

下载: 导出CSV

参考文献(48)

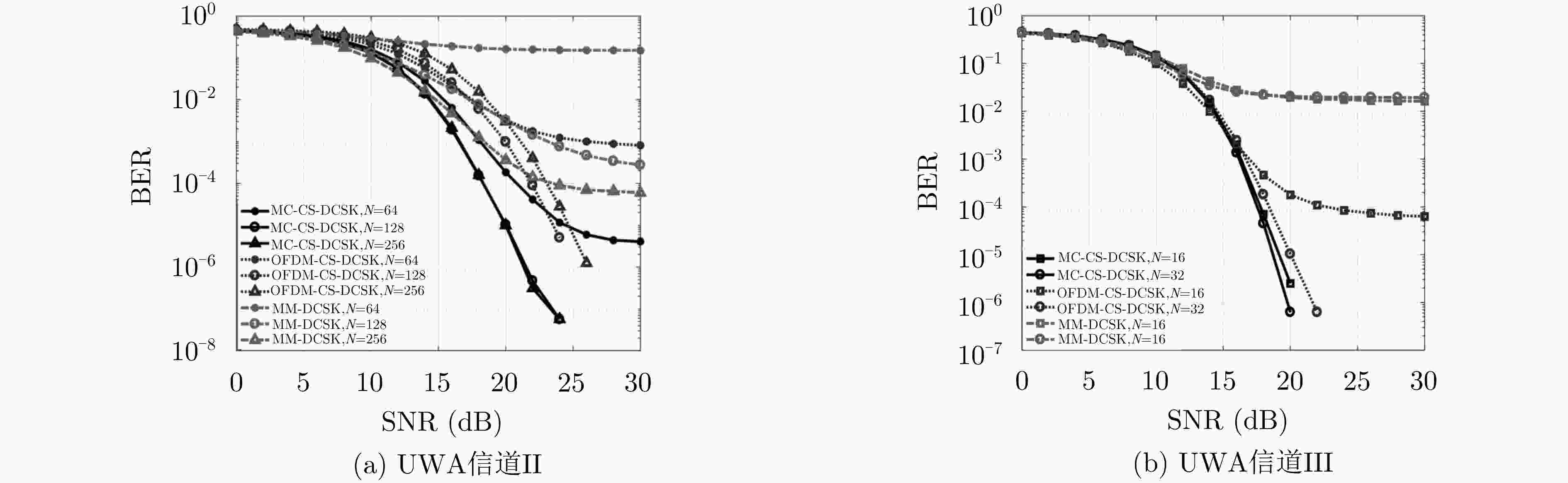
DEDIEU H, KENNEDY M P, and HASLER M. Chaos shift keying: Modulation and demodulation of a chaotic carrier using self-synchronizing Chua’s circuits[J]. IEEE Transactions on Circuits and Systems Ⅱ: Analog and Digital Signal Processing, 1993, 40(10): 634–642. doi: 10.1109/82.246164

KOLUMBAN G, VIZVARI B, SCHWARZ W, et al. Differential chaos shift keying: A robust coding for chaos communication[C]. The 4th International Workshop on Nonlinear Dynamics of Electronic Systems, Seville, Spain: NDES, 1996: 87–92.

KENNEDY M P, KOLUMBAN G, KIS G, et al. Performance evaluation of FM-DCSK modulation in multipath environments[J]. IEEE Transactions on Circuits and Systems I: Fundamental Theory and Applications, 2000, 47(12): 1702–1711. doi: 10.1109/81.899922

WANG Lin, ZHANG Chaoxian, and CHEN Guanrong. Performance of an SIMO FM-DCSK communication system[J]. IEEE Transactions on Circuits and Systems Ⅱ: Express Briefs, 2008, 55(5): 457–461. doi: 10.1109/TCSⅡ.2007.914895

KADDOUM G, SOUJERI E, ARCILA C, et al. I-DCSK: An improved noncoherent communication system architecture[J]. IEEE Transactions on Circuits and Systems Ⅱ: Express Briefs, 2015, 62(9): 901–905. doi: 10.1109/TCSⅡ.2015.2435831

YANG Hua, JIANG Guoping, and DUAN Junyi. Phase-separated DCSK: A simple delay-component-free solution for chaotic communications[J]. IEEE Transactions on Circuits and Systems Ⅱ: Express Briefs, 2014, 61(12): 967–971. doi: 10.1109/TCSⅡ.2014.2356914

KADDOUM G and SOUJERI E. NR-DCSK: A noise reduction differential chaos shift keying system[J]. IEEE Transactions on Circuits and Systems Ⅱ: Express Briefs, 2016, 63(7): 648–652. doi: 10.1109/TCSⅡ.2016.2532041

KADDOUM G, RICHARDSON F D, and GAGNON F. Design and analysis of a multi-carrier differential chaos shift keying communication system[J]. IEEE Transactions on Communications, 2013, 61(8): 3281–3291. doi: 10.1109/TCOMM.2013.071013.130225

HUANG Tingting, WANG Lin, XU Weikai, et al. A multi-carrier M-Ary differential chaos shift keying system with low PAPR[J]. IEEE Access, 2017, 5: 18793–18803. doi: 10.1109/ACCESS.2017.2752238

CHENG Guixian, WANG Lin, CHEN Qiwang, et al. Design and performance analysis of generalised carrier index M-ary differential chaos shift keying modulation[J]. IET Communications, 2018, 12(11): 1324–1331. doi: 10.1049/iet-com.2017.0800

YANG Hua, JIANG Guoping, TANG W K S, et al. Multi-carrier differential chaos shift keying system with subcarriers allocation for noise reduction[J]. IEEE Transactions on Circuits and Systems Ⅱ: Express Briefs, 2018, 65(11): 1733–1737. doi: 10.1109/TCSⅡ.2017.2752754

LU Yazhen, MIAO Meiyuan, WANG Lin, et al. A multilevel code-shifted differential chaos shift keying system with reference diversity[J]. IEEE Transactions on Circuits and Systems Ⅱ: Express Briefs, 2020, 67(11): 2462–2466. doi: 10.1109/TCSⅡ.2020.2964883

KADDOUM G and GAGNON F. Design of a high-data-rate differential chaos-shift keying system[J]. IEEE Transactions on Circuits and Systems Ⅱ: Express Briefs, 2012, 59(7): 448–452. doi: 10.1109/TCSⅡ.2012.2198982

CHEN Pingping, WANG Lin, and CHEN Guanrong. DDCSK-Walsh coding: A reliable chaotic modulation-based transmission technique[J]. IEEE Transactions on Circuits and Systems Ⅱ: Express Briefs, 2012, 59(2): 128–132. doi: 10.1109/TCSⅡ.2011.2180109

CHEN Pingping, SHI Long, FANG Yi, et al. A coded DCSK modulation system over Rayleigh fading channels[J]. IEEE Transactions on Communications, 2018, 66(9): 3930–3942. doi: 10.1109/TCOMM.2018.2827032

HUANG Tingting, WANG Lin, XU Weikai, et al. Multilevel code-shifted differential-chaos-shift-keying system[J]. IET Communications, 2016, 10(10): 1189–1195. doi: 10.1049/iet-com.2015.1109

MIAO Meiyuan, WANG Lin, KATZ M, et al. Hybrid modulation scheme combining PPM with differential chaos shift keying modulation[J]. IEEE Wireless Communications Letters, 2019, 8(2): 430–433. doi: 10.1109/LWC.2018.2871137

XU Weikai and WANG Lin. CIM-DCSK: A differential chaos shift keying scheme with code-index modulation[C]. The 16th International Symposium on Communications and Information Technologies, Qingdao, China, 2016: 26–28. doi: 10.1109/ISCIT.2016.7751600.

TAN Yunsheng, XU Weikai, HUANG Tingting, et al. A multilevel code shifted differential chaos shift keying scheme with code index modulation[J]. IEEE Transactions on Circuits and Systems Ⅱ: Express Briefs, 2018, 65(11): 1743–1747. doi: 10.1109/TCSⅡ.2017.2764916

XU Weikai, HUANG Tingting, and WANG Lin. Code-shifted differential chaos shift keying with code index modulation for high data rate transmission[J]. IEEE Transactions on Communications, 2017, 65(10): 4285–4294. doi: 10.1109/TCOMM.2017.2725261

SOUJERI E, KADDOUM G, AU M, et al. Frequency index modulation for low complexity low energy communication networks[J]. IEEE Access, 2017, 5: 23276–23287. doi: 10.1109/ACCESS.2017.2713721

HERCEG M, VRANJEŠ D, KADDOUM G, et al. Commutation code index DCSK modulation technique for high-data-rate communication systems[J]. IEEE Transactions on Circuits and Systems Ⅱ: Express Briefs, 2018, 65(12): 1954–1958. doi: 10.1109/TCSⅡ.2018.2817930

YANG Hua, TANG Wallace K S, CHEN Guanrong, et al. System design and performance analysis of orthogonal multi-level differential chaos shift keying modulation scheme[J]. IEEE Transactions on Circuits and Systems I: Regular Papers, 2016, 63(1): 146–156. doi: 10.1109/TCSI.2015.2510622

GALIAS Z and MAGGIO G M. Quadrature chaos-shift keying: Theory and performance analysis[J]. IEEE Transactions on Circuits and Systems I: Fundamental Theory and Applications, 2001, 48(12): 1510–1519. doi: 10.1109/TCSI.2001.972858

WANG Shiliang and WANG Xiaodong. M-DCSK-based chaotic communications in MIMO multipath channels with no channel state information[J]. IEEE Transactions on Circuits and Systems Ⅱ: Express Briefs, 2010, 57(12): 1001–1005. doi: 10.1109/TCSⅡ.2010.2083091

WANG Lin, CAI Guofa, and CHEN G R. Design and performance analysis of a new multiresolution M-Ary differential chaos shift keying communication system[J]. IEEE Transactions on Wireless Communications, 2015, 14(9): 5197–5208. doi: 10.1109/TWC.2015.2434820

CAI Guofa, FANG Yi, HAN Guojun, et al. A square-constellation-based M-Ary DCSK communication system[J]. IEEE Access, 2016, 4: 6295–6303. doi: 10.1109/ACCESS.2016.2612224

CAI Guofa, FANG Yi, and HAN Guojun. Design of an adaptive multiresolution M-Ary DCSK system[J]. IEEE Communications Letters, 2017, 21(1): 60–63. doi: 10.1109/LCOMM.2016.2614682

CAI Guofa, FANG Yi, HAN Guojun, et al. A new hierarchical M-Ary DCSK communication system: Design and Analysis[J]. IEEE Access, 2017, 5: 17414–17424. doi: 10.1109/ACCESS.2017.2740973

GHOSH M. Analysis of the effect of impulse noise on multicarrier and single carrier QAM systems[J]. IEEE Transactions on Communications, 1996, 44(2): 145–147. doi: 10.1109/26.486604

HE Yanchun WANG Lin, ZHOU Chenglong, et al. A novel trellis-coded differential chaotic modulation system[C]. 2017 Wireless Telecommunications Symposium, Chicago, USA, 2017: 1–6. doi: 10.1109/WTS.2017.7943522.

ZHOU Chenglong, HU Wei, WANG Lin, et al. Turbo trellis-coded differential chaotic modulation[J]. IEEE Transactions on Circuits and Systems Ⅱ: Express Briefs, 2018, 65(2): 191–195. doi: 10.1109/TCSⅡ.2017.2709347

ZHOU Chenglong, HU Wei, WANG Lin, et al. IQ-interleaved turbo trellis-coded differential chaotic modulation scheme[C]. The 23rd Asia-Pacific Conference on Communications, Perth, Australia, 2017: 1–6. doi: 10.23919/APCC.2017.8304013.

ZHANG Bangquan, WANG Lin, ZHOU Chenglong, et al. Serial concatenated trellis-coded differential chaotic modulation[C]. The 29th IEEE Annual International Symposium on Personal, Indoor and Mobile Radio Communications, Bologna, Italy, 2018: 1–5. doi: 10.1109/PIMRC.2018.8580688.

ZHAN Jia WANG Lin, KATZ M, et al. A differential chaotic bit-interleaved coded modulation system over multipath Rayleigh channels[J]. IEEE Transactions on Communications, 2017, 65(12): 5257–5265. doi: 10.1109/TCOMM.2017.2719030

DIVSALAR D and JONES C. Protograph based low error floor LDPC coded modulation[C]. 2005 IEEE Military Communications Conference, Atlantic City, USA, 2005: 378–385. doi: 10.1109/MILCOM.2005.1605713.

ABBASFAR A, DIVSALAR D, and YAO K. Accumulate-repeat-accumulate codes[J]. IEEE Transactions on Communications, 2007, 55(4): 692–702. doi: 10.1109/TCOMM.2007.894109

洪少华, 王琳. 基于原模图LDPC码的分布式联合信源信道编码[J]. 电子与信息学报, 2017, 39(11): 2594–2599. doi: 10.11999/JEIT170113

HONG Shaohua and WANG Lin. Protograph LDPC based distributed joint source channel coding[J]. Journal of Electronics &Information Technology, 2017, 39(11): 2594–2599. doi: 10.11999/JEIT170113

陶雄飞, 王跃东, 柳盼. 基于变量节点更新的LDPC码加权比特翻转译码算法[J]. 电子与信息学报, 2016, 38(3): 688–693. doi: 10.11999/JEIT150720

TAO Xiongfei, WANG Yuedong, and LIU Pan. Weighted bit-flipping decoding algorithm for LDPC codes based on updating of variable nodes[J]. Journal of Electronics &Information Technology, 2016, 38(3): 688–693. doi: 10.11999/JEIT150720

KADDOUM G and TADAYON N. Differential chaos shift keying: A robust modulation scheme for power-line communications[J]. IEEE Transactions on Circuits and Systems Ⅱ: Express Briefs, 2017, 64(1): 31–35. doi: 10.1109/TCSⅡ.2016.2546901

ZHENG Mingyang, HUANG Tingting, WANG Lin, et al. Performance analysis of M-ary DCSK system over narrow band power-line communications[C]. The 23rd Asia-Pacific Conference on Communications, Perth, Australia, 2017: 1–6. doi: 10.23919/APCC.2017.8304008.

CHENG LIN and FERREIRA H C. Time-diversity permutation coding scheme for narrow-band power-line channels[C]. 2017 IEEE International Symposium on Power Line Communications and its Applications, Beijing, China, 2012: 378–385. doi: 10.1109/ISPLC.2012.6201335.

ZHANG Yuyang, WANG Lin, CHEN Qiwang, et al. Optimization of constellation-based DC-BICM systems over power line channels[C]. The 29th IEEE Annual International Symposium on Personal, Indoor and Mobile Radio Communications, Bologna, Italy, 2018: 576–577. doi: 10.1109/PIMRC.2018.8580673.

CHEN Qiwang, WANG Lin, LÜ Yibo, et al. Designing protograph-based LDPC Codes for iterative receivers on M-ary DCSK Systems[J]. IEEE Transactions on Circuits and Systems Ⅱ: Express Briefs, 2018, 65(4): 466–470. doi: 10.1109/TCSⅡ.2017.2741062

杨帆, 贾辉, 刘宝树, 等. α稳定脉冲噪声下宽带电力线通信系统性能分析[J]. 电子与信息学报, 2019, 41(6): 1374–1380. doi: 10.11999/JEIT180261

YANG Fan, JIA Hui, LIU Baoshu, et al. Performance analysis of broadband power-line communications systems under the alpha-stable impulsive noise[J]. Journal of Electronics &Information Technology, 2019, 41(6): 1374–1380. doi: 10.11999/JEIT180261

罗忠涛, 詹燕梅, 郭人铭, 等. 脉冲噪声中基于指数函数的可变拖尾非线性变换设计[J]. 电子与信息学报, 2020, 42(4): 932–940. doi: 10.11999/JEIT190401

LUO Zhongtao, ZHAN Yanmei, GUO Renming, et al. Variable tailing nonlinear transformation design based on exponential function in impulsive noise[J]. Journal of Electronics &Information Technology, 2020, 42(4): 932–940. doi: 10.11999/JEIT190401

CHEN Menglei, XU Weikai, WANG Deiqing, et al. Multi-carrier chaotic communication scheme for underwater acoustic communications[J]. IET Communications, 2019, 13(14): 2097–2105. doi: 10.1049/iet-com.2018.5524

QU Fengzhou, QIN Xiangzhao, YANG Liuqing, et al. Spread-spectrum method using multiple sequences for underwater acoustic communications[J]. IEEE Journal of Oceanic Engineering, 2018, 43(4): 1215–1226. doi: 10.1109/JOE.2017.2750298

施引文献

资源附件(0)

访问统计