Multi-target Interference Localization Using Single Satellite Multi-beam Antenna Based on Compressive Sensing
-
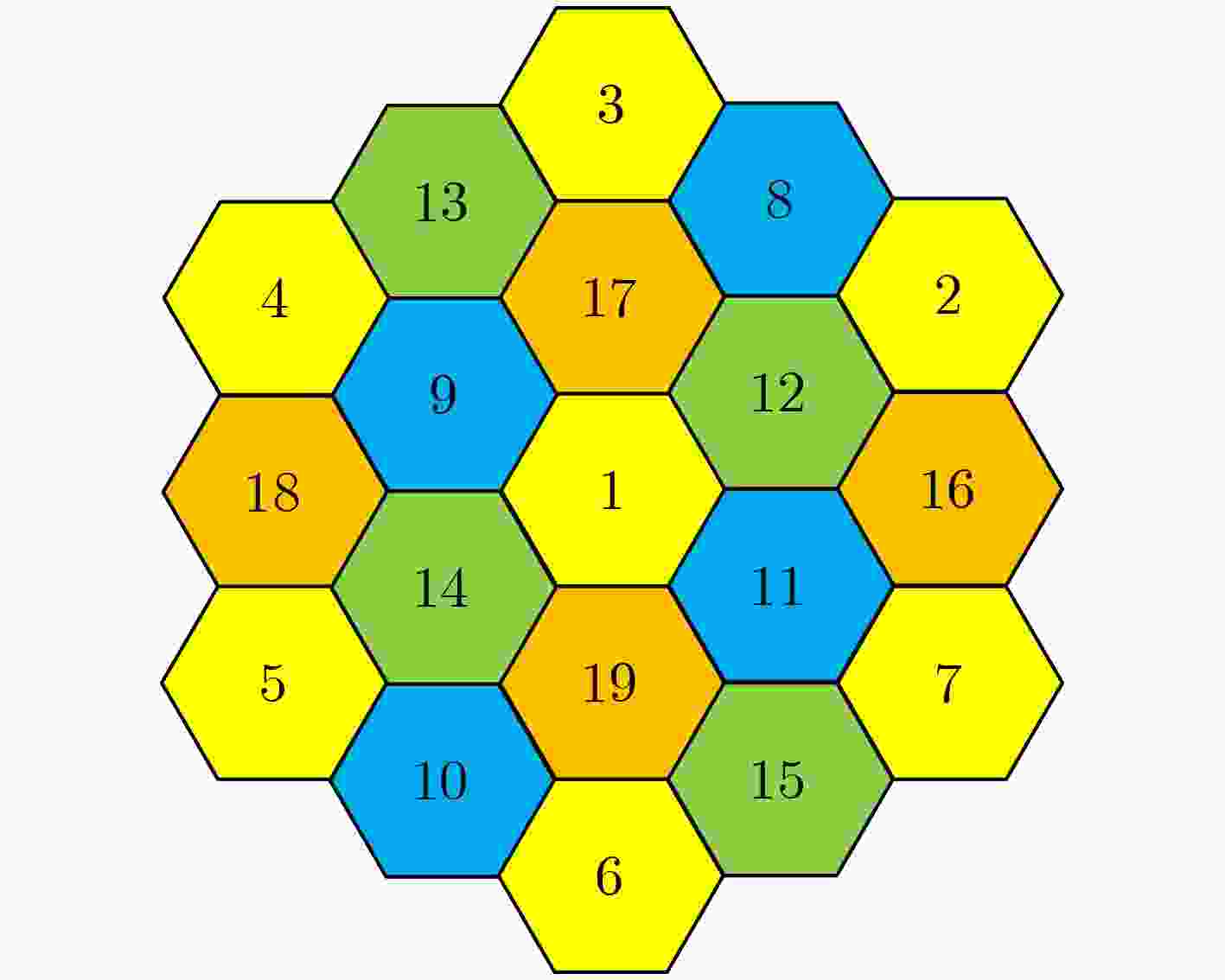
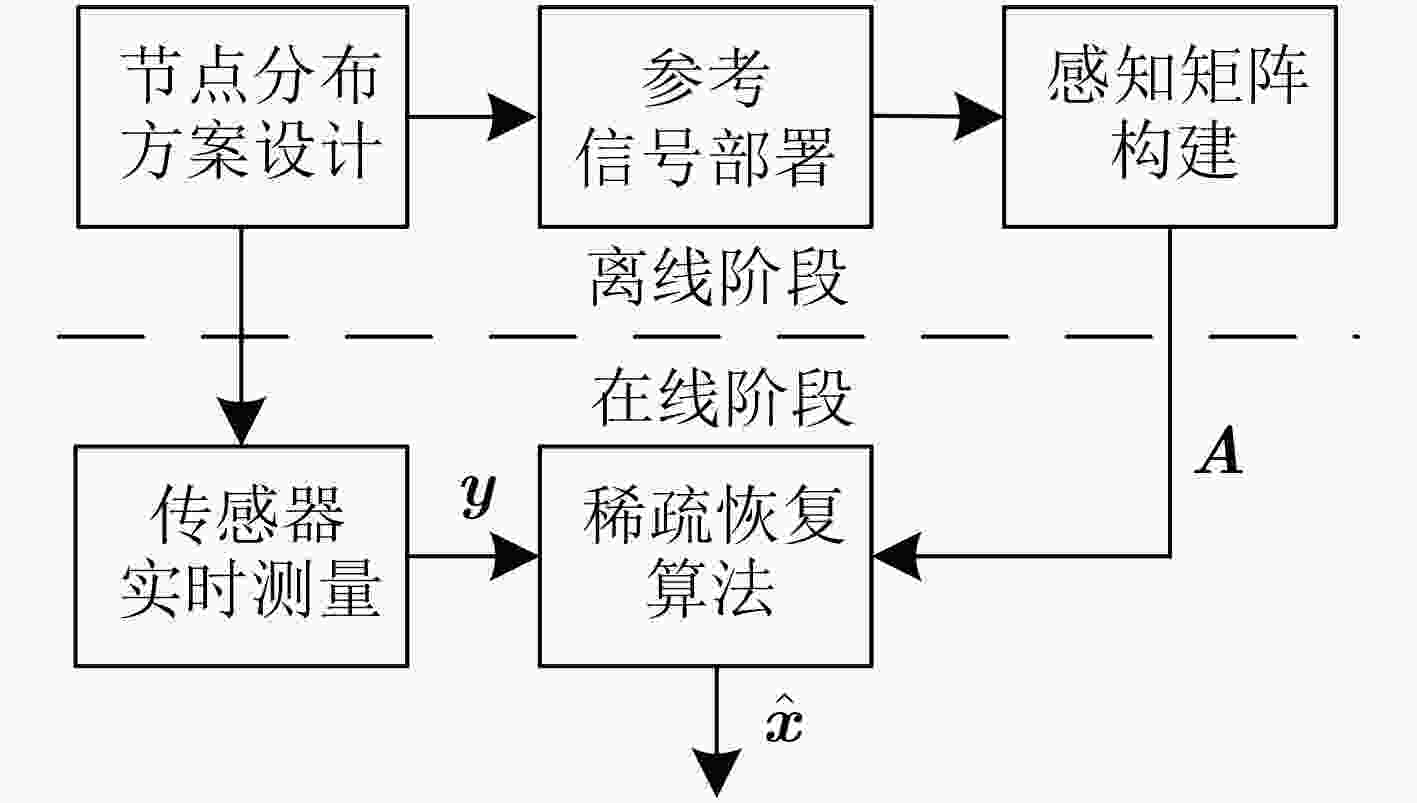
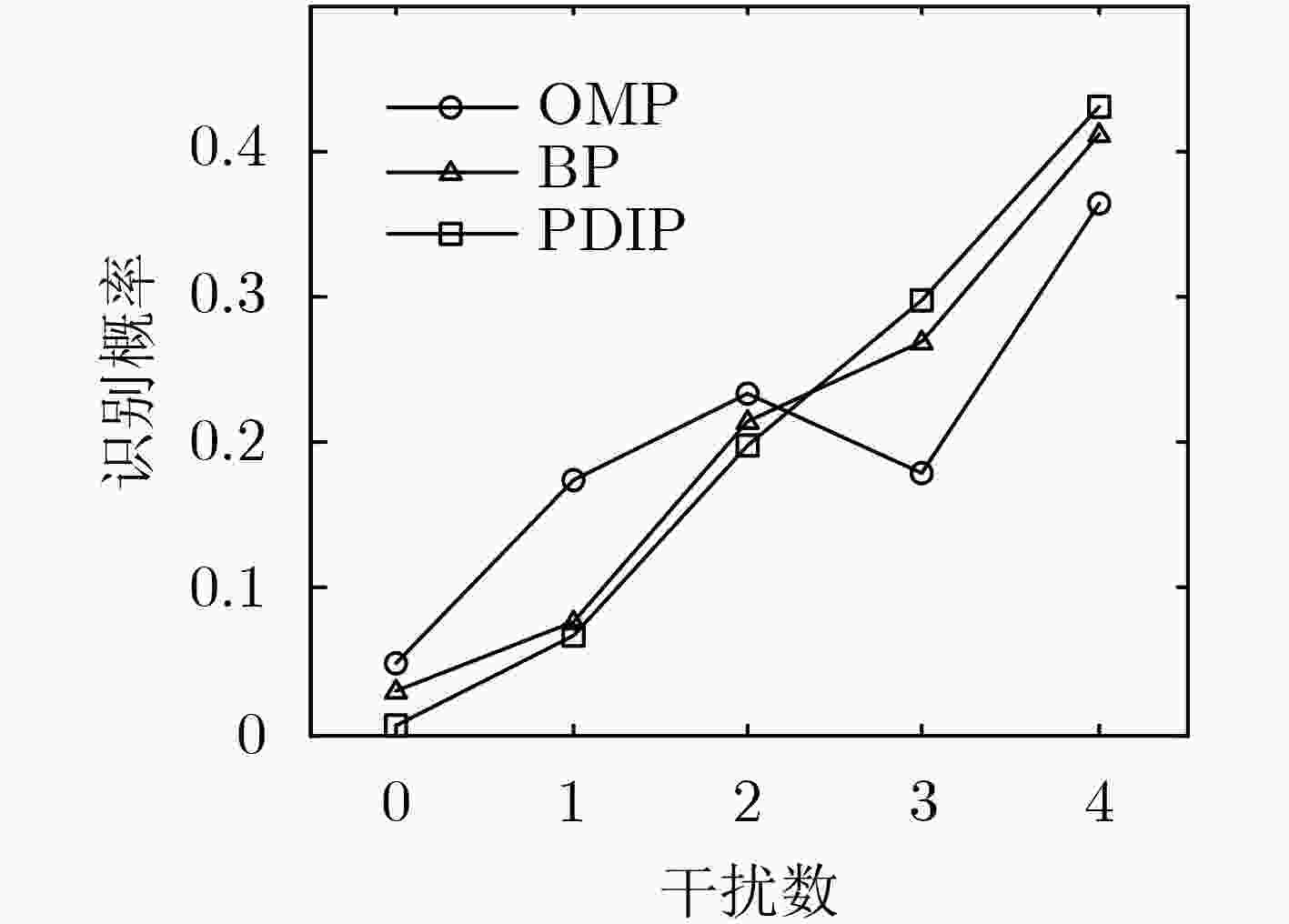
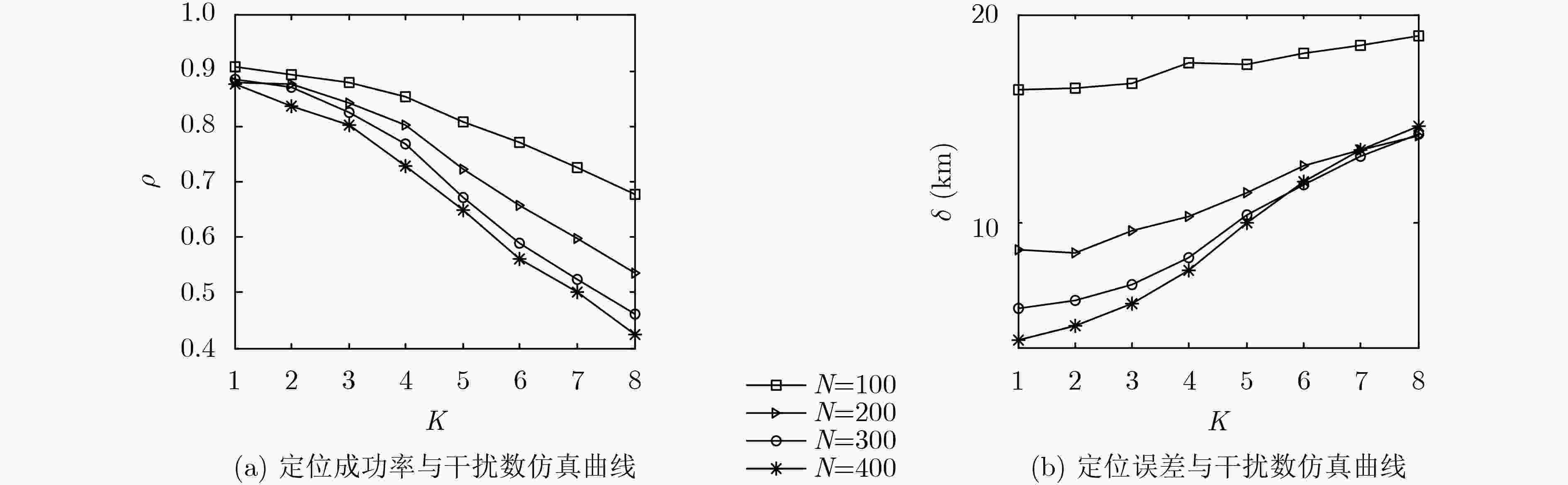
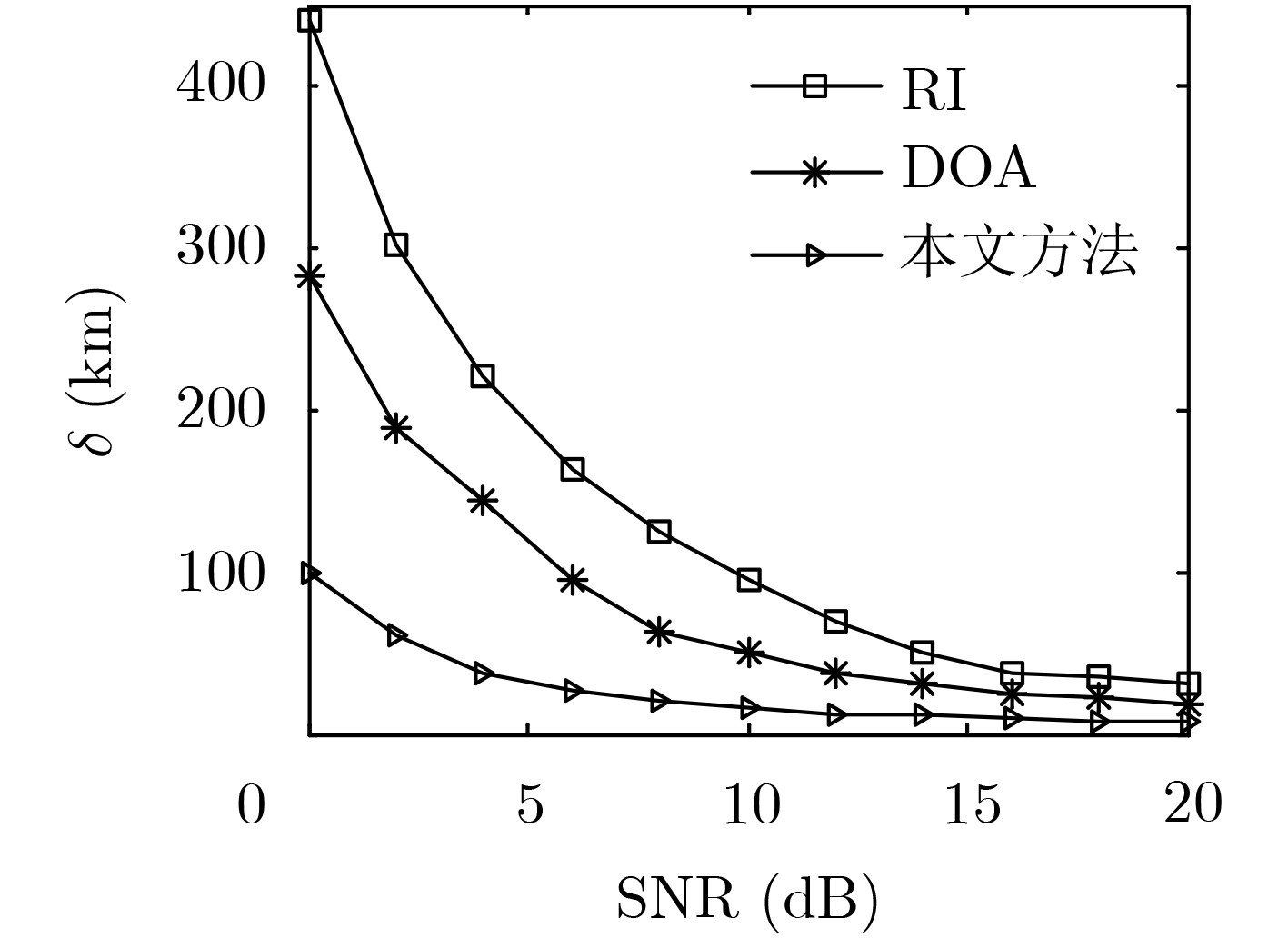
摘要: 针对卫星干扰处理中的多目标定位问题,该文提出基于压缩感知的定位方法。该方法利用目标的空间稀疏性,以及多波束天线在不同信号源方向上的增益不同,仅需要测量接收信号强度便可实现多个干扰的位置识别。研究结果表明,定位性能与节点分布、目标个数、波束覆盖半径、判决门限有关。在给定参数及原对偶内点算法下,该方法可实现1~4个干扰源的空域定位,在信噪比为20 dB时定位精度达到7.7 km,优于经典的旋转干涉仪和空间谱估计测向方法。Abstract: To cope with the issue of locating multi-target in mitigating satellite interference, a localization method is proposed based on Compressive Sensing (CS). The sources of satellite interference can be identified by using Received Signal Strength (RSS) measurement only, relying on the spatial sparsity of the target source and the fact that multi-beam antenna has different gain at the position of interference. The conclusions show that positioning performance is related to node distribution, target number, coverage radius and decision threshold. Furthermore, over the Primal-Dual Interior Point (PDIP) algorithm, the simulation result represents that the target number is four under certain conditions, and the position accuracy is closed to 7.7 km with SNR of 20 dB. In addition, the study result also confirms that the proposed algorithm is better than the classic methods of Rotating Interferometer (RI) and Direction Of Arrival (DOA) estimation
-
表 1 仿真参数配置
固定参数 取值 调整参数 取值 波束数M 19 载波频率f(GHz) 3.60~3.75 天线口径D(m) 14 功率系数k 1~5 天线效率$\eta $ 0.6 节点数N 400 蜂窝边长l(km) 240 干扰数K 4 区域半径R(km) 1050 覆盖半径r(km) 4l 搜索半径s(km) 30 判决门限T 0.2 参考功率P0 1 信噪比(dB) 20 表 2 评价指标与关键参数对应关系
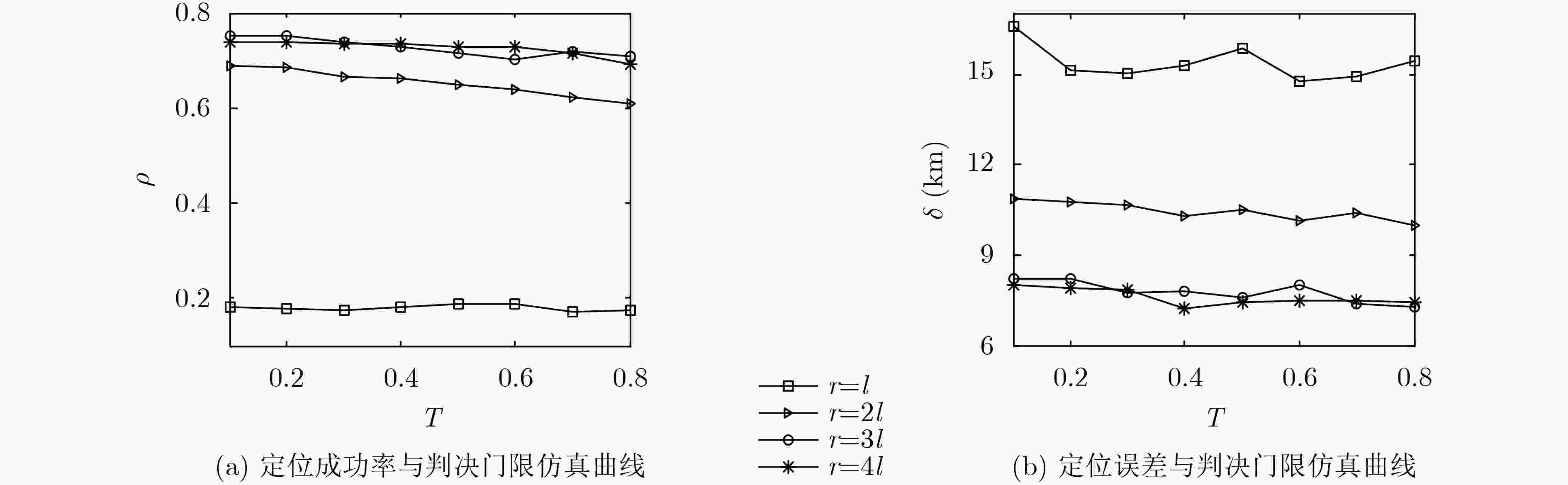
定位成功率$\rho $ 定位误差$\delta $ 节点数N – – 干扰数K – + 覆盖半径r + – 判决门限T – / -
[1] 易克初, 李怡, 孙晨华, 等. 卫星通信的近期发展与前景展望[J]. 通信学报, 2015, 36(6): 157–172. doi: 10.11959/j.issn.1000-436x.2015223YI Kechu, LI Yi, SUN Chenhua, et al. Recent development and its prospect of satellite communications[J]. Journal on Communications, 2015, 36(6): 157–172. doi: 10.11959/j.issn.1000-436x.2015223 [2] 郝才勇. 卫星干扰处理技术综述[J]. 电信科学, 2017, 8(1): 106–113. doi: 10.11959/j.issn.1000-0801.2017018HAO Caiyong. A survey of mitigating satellite interference technology[J]. Telecommunications Science, 2017, 8(1): 106–113. doi: 10.11959/j.issn.1000-0801.2017018 [3] 孙霆, 董春曦, 毛昱. 一种基于半定松弛技术的TDOA-FDOA无源定位算法[J]. 电子与信息学报, 2020, 42(7): 1599–1605. doi: 10.11999/JEIT190435SUN Ting, DONG Chunxi, and MAO Yu. A TDOA-FDOA passive positioning algorithm based on the semi-definite relaxation technique[J]. Journal of Electronics &Information Technology, 2020, 42(7): 1599–1605. doi: 10.11999/JEIT190435 [4] 孙光才, 王裕旗, 高昭昭, 等. 一种基于短合成孔径的双星干涉精确定位方法[J]. 电子与信息学报, 2020, 42(2): 472–479. doi: 10.11999/JEIT180940SUN Guangcai, WANG Yuqi, GAO Zhaozhao, et al. A dual satellite interferometric precise localization method based on short synthetic aperture[J]. Journal of Electronics &Information Technology, 2020, 42(2): 472–479. doi: 10.11999/JEIT180940 [5] 张金秀, 陶海红, 王渊. 一种基于双基线旋转的改进干涉仪定位算法[J]. 北京理工大学学报, 2018, 38(3): 320–324. doi: 10.15918/j.tbit1001-0645.2018.03.016ZHANG Jinxiu, TAO Haihong, and WANG Yuan. An improved locating algorithm based on double baselines rotating interferometer[J]. Transactions of Beijing Institute of Technology, 2018, 38(3): 320–324. doi: 10.15918/j.tbit1001-0645.2018.03.016 [6] ADEOGUN R O. A robust music based scheme for interference location in satellite systems with multibeam antennas[J]. International Journal of Computer Applications, 2013, 82(12): 1–6. doi: 10.5120/14165-2322 [7] 徐义, 郭福成, 冯道旺. 一种单星仅测TOA无源定位方法[J]. 宇航学报, 2010, 31(2): 502–508. doi: 10.3873/j.issn.1000-1328.2010.02.031XU Yi, GUO Fucheng, and FENG Daowang. A new satellite passive localization method using TOA measurement only[J]. Journal of Astronautics, 2010, 31(2): 502–508. doi: 10.3873/j.issn.1000-1328.2010.02.031 [8] HE Chao, XIE Zhidong, BIAN Dongming, et al. Study of interference localization using single satellite based on signal strength distribution in multi-beam antenna for satellite communications system[J]. International Journal of Distributed Sensor Networks, 2018, 14(5): 16–27. doi: 10.1177/1550147718774015 [9] CANDES E J and WAKIN M B. An introduction to compressive sampling[J]. IEEE Signal Processing Magazine, 2008, 25(2): 21–30. doi: 10.1109/MSP.2007.914731 [10] CEVHER V, DUARTE M F, and BARANIUK R G. Distributed target localization via spatial sparsity[C]. The 2008 16th European Signal Processing Conference, Lausanne, Switzerland: IEEE, 2008: 1–5. doi: 10.5281/zenodo.41257. [11] 余东平, 郭艳, 李宁, 等. 压缩感知多目标无源定位中的字典适配方法[J]. 电子与信息学报, 2019, 41(4): 865–871. doi: 10.11999/JEIT180531YU Dongping, GUO Yan, LI Ning, et al. Dictionary refinement method for compressive sensing based multi-target device-free localization[J]. Journal of Electronics &Information Technology, 2019, 41(4): 865–871. doi: 10.11999/JEIT180531 [12] 游康勇, 杨立山, 郭文彬. 无线传感器网络下基于压缩感知的多目标分层贪婪匹配定位[J]. 自动化学报, 2019, 45(3): 480–489. doi: 10.16383/j.aas.2018.c170237YOU Kangyong, YANG Lishan, and GUO Wenbin. Hierarchical greedy matching pursuit for multi-target localization in wireless sensor networks using compressive sensing[J]. Acta Automatica Sinica, 2019, 45(3): 480–489. doi: 10.16383/j.aas.2018.c170237 [13] CAINI C, CORAZZA G E, FALCIASECCA G, et al. A spectrum- and power-efficient EHF mobile satellite system to be integrated with terrestrial cellular systems[J]. IEEE Journal on Selected Areas in Communications, 1992, 10(8): 1315–1325. doi: 10.1109/49.166759 [14] CANDES E J and TAO T. Decoding by linear programming[J]. IEEE Transactions on Information Theory, 2005, 51(12): 4203–4215. doi: 10.1109/TIT.2005.858979 [15] BOYD S and VANDENBERGHE L. Convex Optimization[M]. Cambridge: Cambridge University Press, 2004. doi: 10.1017/CBO9780511804441. [16] CANDÈS E J, ROMBERG J K, and TAO T. Stable signal recovery from incomplete and inaccurate measurements[J]. Communications on Pure and Applied Mathematics, 2006, 59(8): 1207–1223. doi: 10.1002/cpa.20124 -





 下载:
下载:


 下载:
下载:
