Joint Transmitted Waveform and Mismatched Filter Design against Interrupted-sampling Repeater Jamming
-
摘要: 间歇采样转发干扰(ISRJ)是基于欠采样原理的新型雷达相干干扰技术,能够形成密集假目标干扰。该文针对抗间歇采样转发干扰问题,提出一种雷达发射波形和非匹配滤波联合设计的抗干扰方法。首先,以发射信号脉冲压缩积分旁瓣能量和干扰信号非匹配滤波输出积分能量为目标函数,综合考虑发射信号的幅度约束,建立了间歇采样转发干扰抑制的数学优化模型。然后,通过问题分解推导了雷达发射波形和非匹配滤波器的解析表达式,基于迭代算法设计了发射波形和非匹配滤波器。最后,通过仿真实验的方式验证了发射波形和非匹配滤波器的性能、抗间歇采样转发干扰性能以及所提方法的间歇采样转发干扰抑制能力。Abstract: Interrupted-Sampling Repeater Jamming (ISRJ) is an advanced radar coherent interference based on the principle of under-sampling method, and achieves a train of false targets. In this paper, a joint transmitted waveform and mismatched filter design method focus on suppressing the ISRJ is proposed. Firstly, the mathematical optimization model is established by minimizing the transmitted signal pulse compression integrated sidelobe level and jamming signal mismatched filter output integrated level under the constraint of constant modulus waveform. Secondly, the analytical solution of transmitted waveform and mismatched filter is obtained by simplifing the optimization problem. By utilizing cyclic iterative algorithm, unimodular waveform and mismatched filter are produced. Finally, simulations are presented to assess the waveform and filter performance and anti-ISRJ performance. Simulation results demonstrated that the ISRJ is suppressed by jointly designing the waveform and filter.
-
表 1 抑制ISRJ的恒模波形和非匹配滤波器设计流程
(1) 利用随机相位编码信号初始化${{x}}$, ${{y}}$和${{h}}$;利用随机序列初始
化${{\lambda}}$和$\mu ,\nu $;(2) 固定恒模波形${{x}}$和中间变量${{y}}$,利用式(10)计算非匹配滤波${{h}}$; (3) 固定非匹配滤波${{h}}$和中间变量${{y}}$,利用式(14)计算恒模波形${{x}}$; (4) 固定恒模波形${{x}}$和非匹配滤波${{h}}$,利用式(16)计算中间变量${{y}}$; (5) 更新利用式(13d)和式(13e)分别更新${{\lambda}}$和$\mu ,\nu $; (6) 重复步骤(3)—步骤(5),直到恒模波形${{x}}$和中间变量${{y}}$的残差满
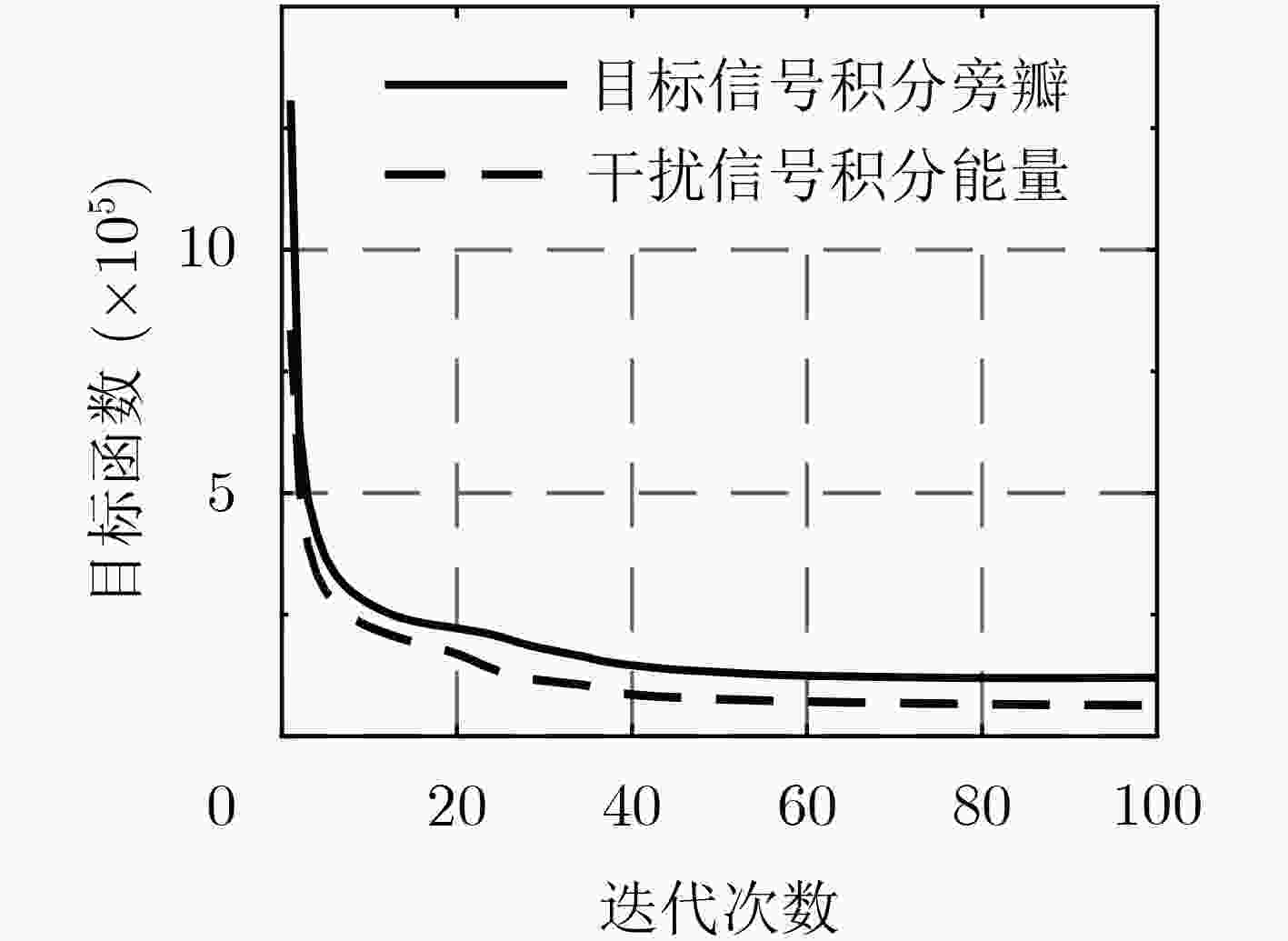
足:${\left\| { {{x - y} } } \right\|^2} \le \delta$;(7) 重复步骤 (2)—步骤(6),直到达到最大迭代次数Itermax。 表 2 仿真参数表
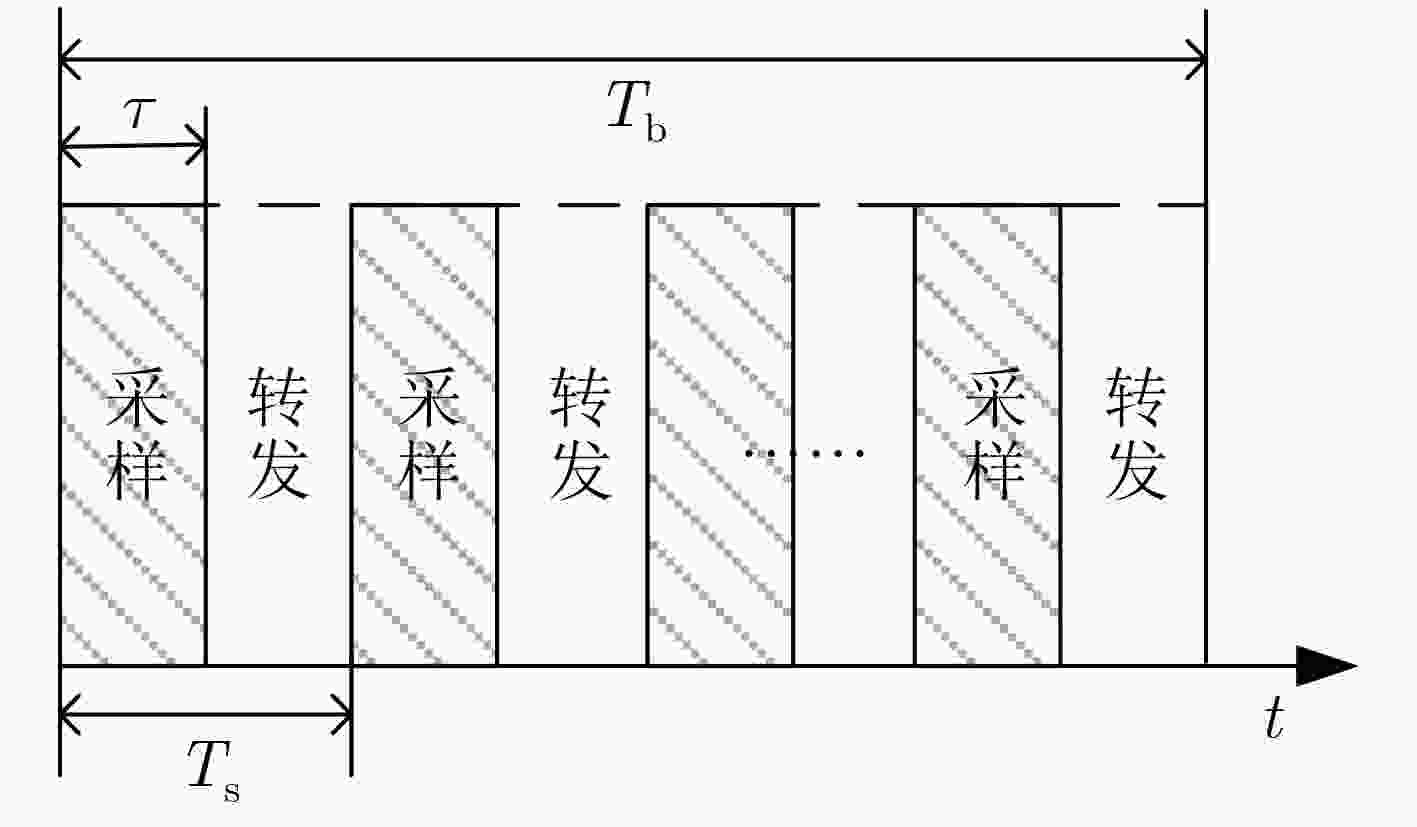
参数 数值 发射信号时宽Tb (μs) 40 间歇采样信号时宽τ (μs) 2 间歇采样周期Ts (μs) 8 算法截止条件δ 1×10–6 最大迭代次数Itermax 100 脉冲压缩归一化峰值bmax (dB) 0 干扰归一化峰值bmin (dB) –30 -
[1] 刘忠, 王雪松, 刘建成, 等. 基于数字射频存储器的间歇采样重复转发干扰[J]. 兵工学报, 2008, 29(4): 405–410. doi: 10.3321/j.issn:1000-1093.2008.04.005LIU Zhong, WANG Xuesong, LIU Jiancheng, et al. Jamming technique of interrupted-sampling and periodic repeater based on digital radio frequency memory[J]. Acta Armamentarii, 2008, 29(4): 405–410. doi: 10.3321/j.issn:1000-1093.2008.04.005 [2] FENG Dejun, XU Letao, PAN Xiaoyi, et al. Jamming wideband radar using interrupted-sampling repeater[J]. IEEE Transactions on Aerospace and Electronic Systems, 2017, 53(3): 1341–1354. doi: 10.1109/TAES.2017.2670958 [3] 吴晓芳, 王雪松, 卢焕章. 对SAR的间歇采样转发干扰研究[J]. 宇航学报, 2009, 30(5): 2043–2048, 2072. doi: 10.3873/j.issn.1000-1328.2009.05.050WU Xiaofang, WANG Xuesong, and LU Huanzhang. Study of intermittent sampling repeater jamming to SAR[J]. Journal of Astronautics, 2009, 30(5): 2043–2048, 2072. doi: 10.3873/j.issn.1000-1328.2009.05.050 [4] 张建中, 穆贺强, 文树梁, 等. 基于LFM分段脉冲压缩的抗间歇采样转发干扰方法[J]. 电子与信息学报, 2019, 41(7): 1712–1720. doi: 10.11999/JEIT180851ZHANG Jianzhong, MU Heqiang, WEN Shuliang, et al. Anti-intermittent sampling repeater jamming method based on LFM segmented pulse compression[J]. Journal of Electronics &Information Technology, 2019, 41(7): 1712–1720. doi: 10.11999/JEIT180851 [5] 周畅, 汤子跃, 朱振波, 等. 抗间歇采样转发干扰的波形设计方法[J]. 电子与信息学报, 2018, 40(9): 2198–2205. doi: 10.11999/JEIT171236ZHOU Chang, TANG Ziyue, ZHU Zhenbo, et al. Anti-interrupted sampling repeater jamming waveform design method[J]. Journal of Electronics &Information Technology, 2018, 40(9): 2198–2205. doi: 10.11999/JEIT171236 [6] 杨伟宏, 陈永光, 王涛. 对波形捷变SAR的间歇采样快/慢时间调制干扰[J]. 系统工程与电子技术, 2012, 34(12): 2456–2462. doi: 10.3969/j.issn.1001-506X.2012.12.09YANG Weihong, CHEN Yongguang, and WANG Tao. Intermittent sampling jamming against waveform agile SAR modulated in fast or slow time[J]. Systems Engineering and Electronics, 2012, 34(12): 2456–2462. doi: 10.3969/j.issn.1001-506X.2012.12.09 [7] 李欣, 王春阳, 包磊, 等. 基于Partial FFT的间歇采样转发干扰抑制方法[J]. 探测与控制学报, 2018, 40(6): 43–49.LI Xin, WANG Chunyang, BAO Lei, et al. Interrupted sampling repeater jamming suppression method based on Partial FFT[J]. Journal of Detection &Control, 2018, 40(6): 43–49. [8] 周超, 刘泉华, 胡程. 间歇采样转发式干扰的时频域辨识与抑制[J]. 雷达学报, 2019, 8(1): 100–106. doi: 10.12000/JR18080ZHOU Chao, LIU Quanhua, and HU Cheng. Time-frequency analysis techniques for recognition and suppression of interrupted sampling repeater jamming[J]. Journal of Radars, 2019, 8(1): 100–106. doi: 10.12000/JR18080 [9] 杨少奇, 田波, 周瑞钊. 利用时频分析的间歇采样干扰对抗方法[J]. 信号处理, 2016, 32(10): 1244–1251. doi: 10.16798/j.issn.1003-0530.2016.10.14YANG Shaoqi, TIAN Bo, and ZHOU Ruizhao. ECCM against interrupted sampling repeater jamming based on time-frequency analysis[J]. Journal of Signal Processing, 2016, 32(10): 1244–1251. doi: 10.16798/j.issn.1003-0530.2016.10.14 [10] GONG Shixian, WEI Xizhang, and LI Xiang. ECCM scheme against interrupted sampling repeater jammer based on time-frequency analysis[J]. Journal of Systems Engineering and Electronics, 2014, 25(6): 996–1003. doi: 10.1109/JSEE.2014.00114 [11] 张建中, 穆贺强, 文树梁, 等. 基于脉内LFM-Costas频率步进的抗间歇采样干扰方法[J]. 系统工程与电子技术, 2019, 41(10): 2170–2177. doi: 10.3969/j.issn.1001-506X.2019.10.03ZHANG Jianzhong, MU Heqiang, WEN Shuliang, et al. Anti-intermittent sampling jamming method based on intra-pulse LFM-Costas frequency stepping[J]. Systems Engineering and Electronics, 2019, 41(10): 2170–2177. doi: 10.3969/j.issn.1001-506X.2019.10.03 [12] 周畅, 范甘霖, 汤子跃, 等. 间歇采样转发干扰的关键参数估计[J]. 太赫兹科学与电子信息学报, 2019, 17(5): 782–787. doi: 10.11805/TKYDA201905.0782ZHOU Chang, FAN Ganlin, TANG Ziyue, et al. Parameter estimation of intermittent sampling repeater jamming[J]. Journal of Terahertz Science and Electronic Information Technology, 2019, 17(5): 782–787. doi: 10.11805/TKYDA201905.0782 [13] 周畅, 汤子跃, 余方利, 等. 基于脉内正交的抗间歇采样转发干扰方法[J]. 系统工程与电子技术, 2017, 39(2): 269–276. doi: 10.3969/j.issn.1001-506X.2017.02.06ZHOU Chang, TANG Ziyue, YU Fangli, et al. Anti intermittent sampling repeater jamming method based on intrapulse orthogonality[J]. Systems Engineering and Electronics, 2017, 39(2): 269–276. doi: 10.3969/j.issn.1001-506X.2017.02.06 [14] KAJENSKI P J. Mismatch filter design via convex optimization[J]. IEEE Transactions on Aerospace and Electronic Systems, 2016, 52(4): 1587–1591. doi: 10.1109/TAES.2016.140556 [15] RABASTE O and SAVY L. Mismatched filter optimization for radar applications using quadratically constrained quadratic programs[J]. IEEE Transactions on Aerospace and Electronic Systems, 2015, 51(4): 3107–3122. doi: 10.1109/TAES.2015.130769 [16] DE MAIO A, HUANG Yongwei, PIEZZO M, et al. Design of radar receive filters optimized according to L p-norm based criteria[J]. IEEE Transactions on Signal Processing, 2011, 59(8): 4023–4029. doi: 10.1109/TSP.2011.2153199 [17] 徐磊磊, 周生华, 刘宏伟, 等. 一种分布式MIMO雷达正交波形和失配滤波器组联合设计方法[J]. 电子与信息学报, 2018, 40(6): 1476–1483. doi: 10.11999/JEIT170836XU Leilei, ZHOU Shenghua, LIU Hongwei, et al. Joint design of distributed MIMO radar orthogonal waveforms and mismatched filter bank[J]. Journal of Electronics &Information Technology, 2018, 40(6): 1476–1483. doi: 10.11999/JEIT170836 [18] 李伟, 王泓霖, 郑家毅, 等. 博弈条件下雷达波形设计策略研究[J]. 电子与信息学报, 2019, 41(11): 2654–2660. doi: 10.11999/JEIT190114LI Wei, WANG Honglin, ZHENG Jiayi, et al. Research on radar waveform design strategy under game condition[J]. Journal of Electronics &Information Technology, 2019, 41(11): 2654–2660. doi: 10.11999/JEIT190114 [19] WU Linlong, BABU P, and PALOMAR D P. Transmit waveform/receive filter design for MIMO radar with multiple waveform constraints[J]. IEEE Transactions on Signal Processing, 2018, 66(6): 1526–1540. doi: 10.1109/TSP.2017.2787115 [20] TANG Bo, TANG Jun, and PENG Yingning. MIMO radar waveform design in colored noise based on information theory[J]. IEEE Transactions on Signal Processing, 2010, 58(9): 4684–4697. doi: 10.1109/TSP.2010.2050885 [21] CHENG Ziyang, HE Zishu, LIAO Bin, et al. MIMO radar waveform design with PAPR and similarity constraints[J]. IEEE Transactions on Signal Processing, 2018, 66(4): 968–981. doi: 10.1109/TSP.2017.2780052 [22] JING Yang, LIANG Junli, ZHOU Deyun, et al. Spectrally constrained unimodular sequence design without spectral level mask[J]. IEEE Signal Processing Letters, 2018, 25(7): 1004–1008. doi: 10.1109/LSP.2018.2836219 [23] HE Hao, LI Jian, and STOICA P. Waveform Design for Active Sensing Systems: A Computational Approach[M]. New York, US: Cambridge University Press, 2012: 39–40. doi: 10.1017/CBO9781139095174. [24] LIANG Junli, SO H C, LI Jian, et al. Unimodular sequence design based on alternating direction method of multipliers[J]. IEEE Transactions on Signal Processing, 2016, 64(20): 5367–5381. doi: 10.1109/TSP.2016.2597123 -





 下载:
下载:


 下载:
下载:
