最大互相关熵多凸组合自适应滤波算法

卢明飞; 彭思愿; 陈霸东

doi:10.11999/JEIT200288

最大互相关熵多凸组合自适应滤波算法

doi: 10.11999/JEIT200288

1.
西安交通大学人工智能与机器人研究所西安 710049
2.
南洋理工大学电气与电子工程学院新加坡 639798

基金项目: 国家自然科学基金-深圳市联合研究项目(U1613219)，国家自然科学基金(91648208, 61976175)

详细信息

作者简介:
卢明飞：男，1987年生，博士生，研究方向为自适应信号处理、模式识别与机器学习等

彭思愿：男，1991年生，博士生，研究方向为非负矩阵分解、信息论学习和自适应滤波算法等

陈霸东：男，1974年生，教授，研究方向为先进信号处理与脑机接口、机器学习与认知计算以及新型神经网络计算模型

通讯作者:
陈霸东　chenbd@mail.xjtu.edu.cn

中图分类号: TN713
计量
- 文章访问数: 1513
- HTML全文浏览量: 1212
- PDF下载量: 183
- 被引次数: 64
出版历程
- 收稿日期: 2020-04-21
- 修回日期: 2020-10-21
- 网络出版日期: 2020-11-18
- 刊出日期: 2021-02-23

Convex Combination of Multiple Adaptive Filters under the Maximum Correntropy Criterion

1.
Institute of Artificial Intelligence and Robotics, Xi’an Jiaotong University, Xi’an 710049, China
2.
School of Electronics and Information Engineering, Nanyang Technological University, 639798, Singapore

Funds: The National Natural Science Foundation-Shenzhen Joint Research Program (U1613219), The National Natural Science Foundation of China (91648208, 61976175)

摘要

摘要: 基于最大互相关熵准则(MCC)的自适应滤波算法在非高斯噪声环境下具有强鲁棒性，得到了广泛应用。然而，传统MCC滤波算法在选择参数时依然受到收敛速度与稳态精度之间固有矛盾的困扰。为解决这一问题，该文提出一类多凸组合MCC算法，能够充分发挥不同参数组合下滤波算法的性能优势，从而获得更好的信道跟踪能力。理论分析得出了所提算法的均值收敛条件和稳态均方误差，同时，仿真实验表明所提算法在对抗高斯和非高斯噪声时均具有收敛快、稳态精度高的特点。
- 自适应滤波 /
- 信道估计 /
- 最大互相关熵准则 /
- 凸组合
Abstract: The adaptive filtering algorithms under the Maximum Correntropy Criterion (MCC) show strong robustness against impulsive noises. The original MCC adaptive filter, however, still suffers from a compromise between convergence rate and misadjustment when choosing parameters. To address this issue, a convex combination approach is proposed in this paper, where multiple MCC adaptive filters with different step-sizes and kernel widths are combined together to yield fast convergence speed and lower misadjustment. Theoretical analysis on convergence of the new approach demonstrates that it can achieve more desirable performance than the original MCC adaptive filter as well as convex combination of two MCC adaptive filers with different step-sizes or kernel widths. Simulation results confirm the excellent performance of the new method.
- Adaptive filtering /
- Channel estimate /
- Maximum Correntropy Criterion(MCC) /
- Convex combination

HTML全文

图 1 算法收敛性能对比

下载: 全尺寸图片幻灯片

图 2 算法凸组合参数收敛过程

下载: 全尺寸图片幻灯片

图 3 改进前后算法收敛过程对比

下载: 全尺寸图片幻灯片

图 4 改进前后算法组合参数收敛过程对比

下载: 全尺寸图片幻灯片

图 5 各种组合算法收敛性能对比1

下载: 全尺寸图片幻灯片

图 6 各种组合算法收敛性能对比2

下载: 全尺寸图片幻灯片

表 1 算法参数设置

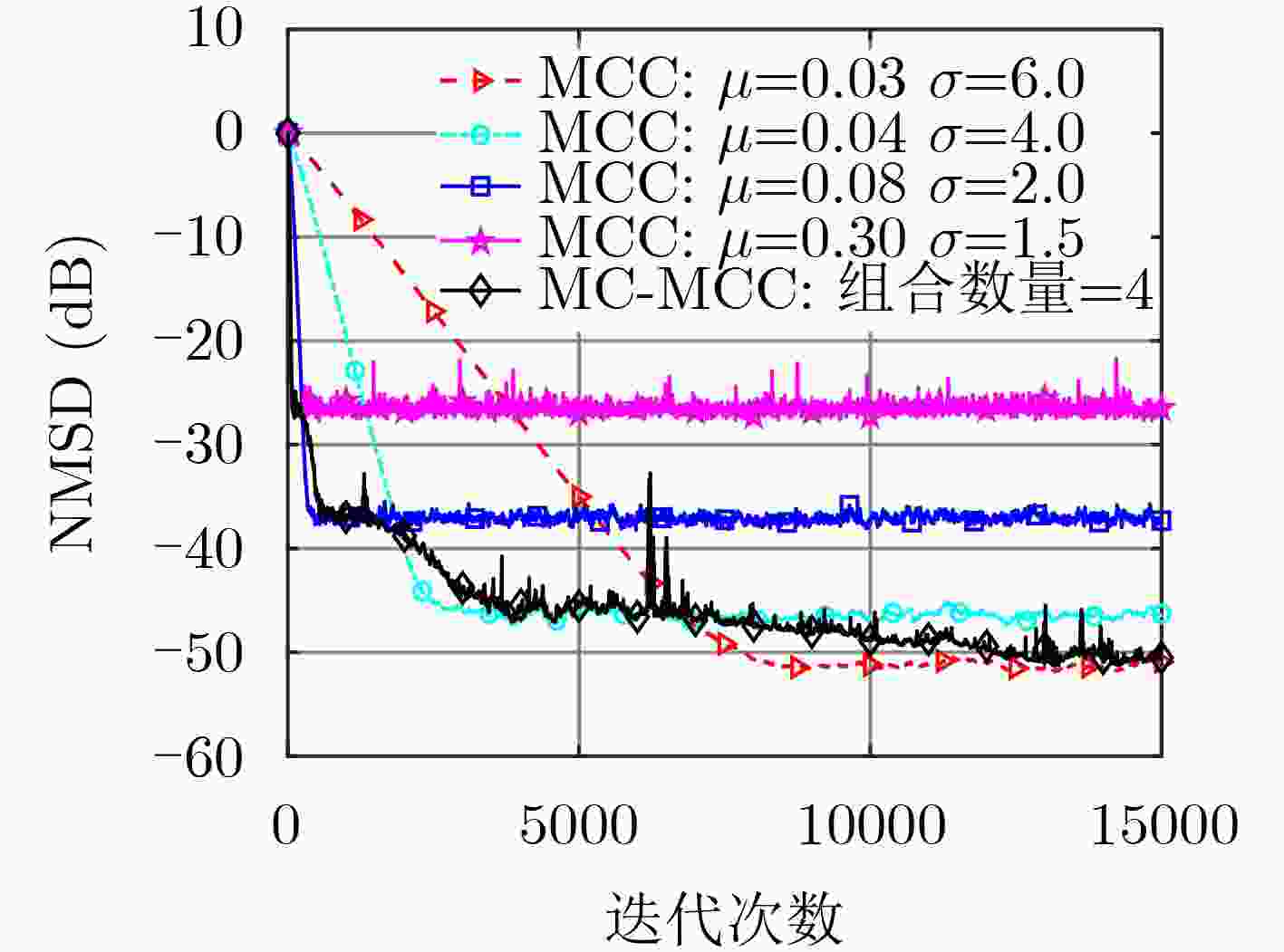
名称 ${\mu _1}$ / ${\sigma _1}$ ${\mu _2}$ / ${\sigma _2}$ ${\mu _3}$ / ${\sigma _3}$ ${\mu _4}$ / ${\sigma _4}$ ${\mu _\xi }$ / ${\sigma _\xi }$

数值 0.03/6.0 0.04/4.0 0.08/2.0 0.3/1.5 4.5/1.0

下载: 导出CSV

表 2 算法参数设置

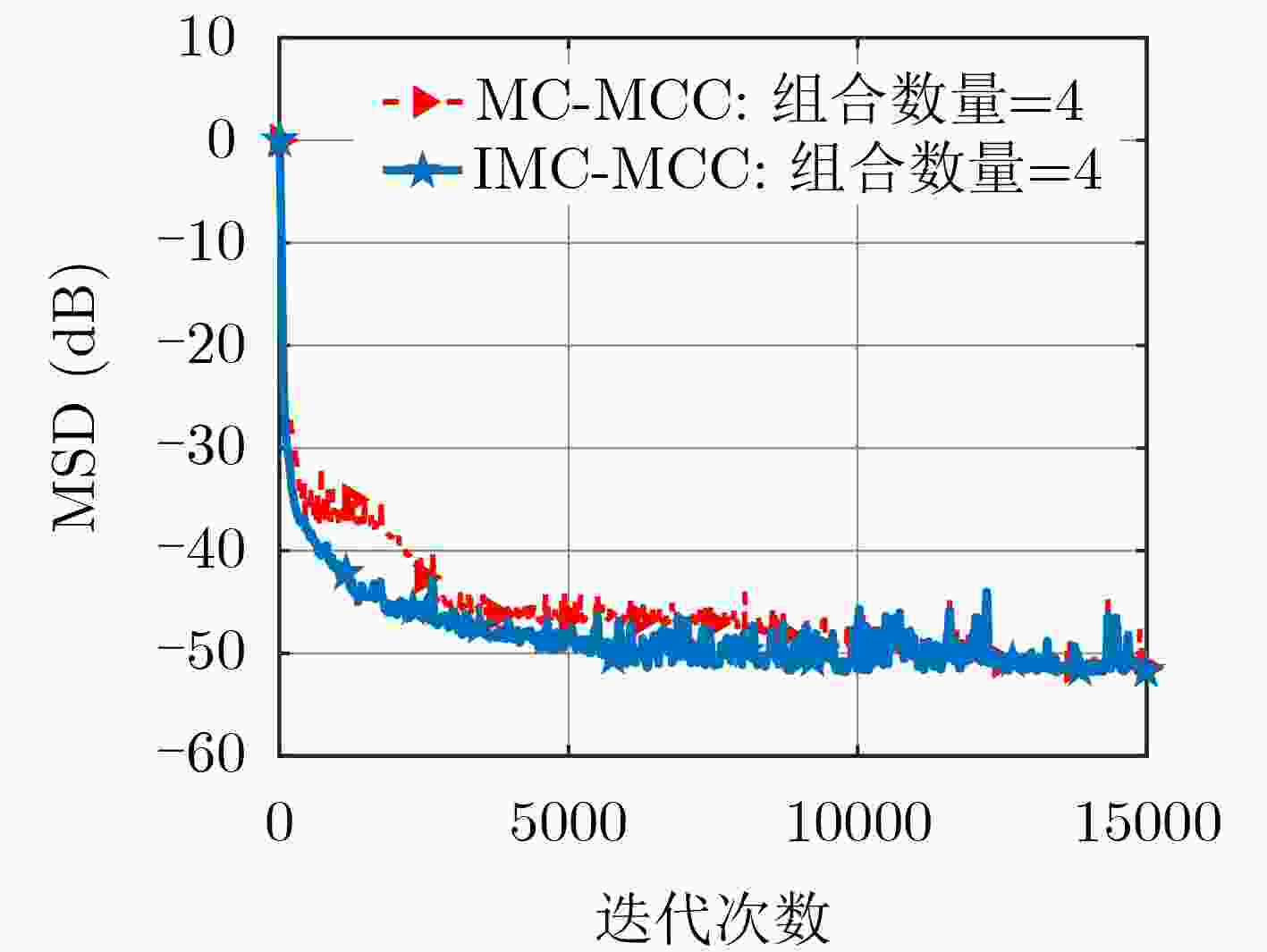
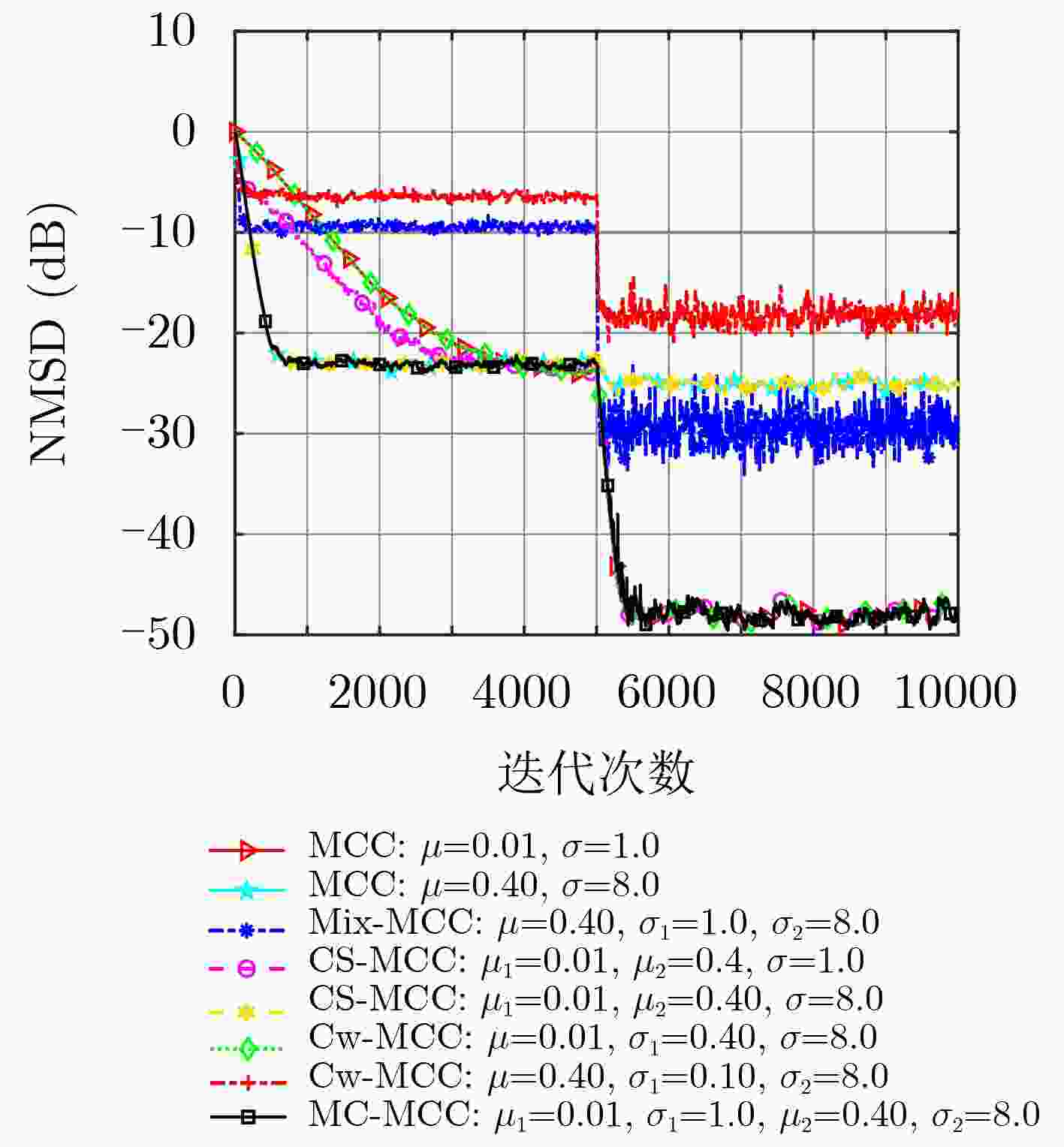
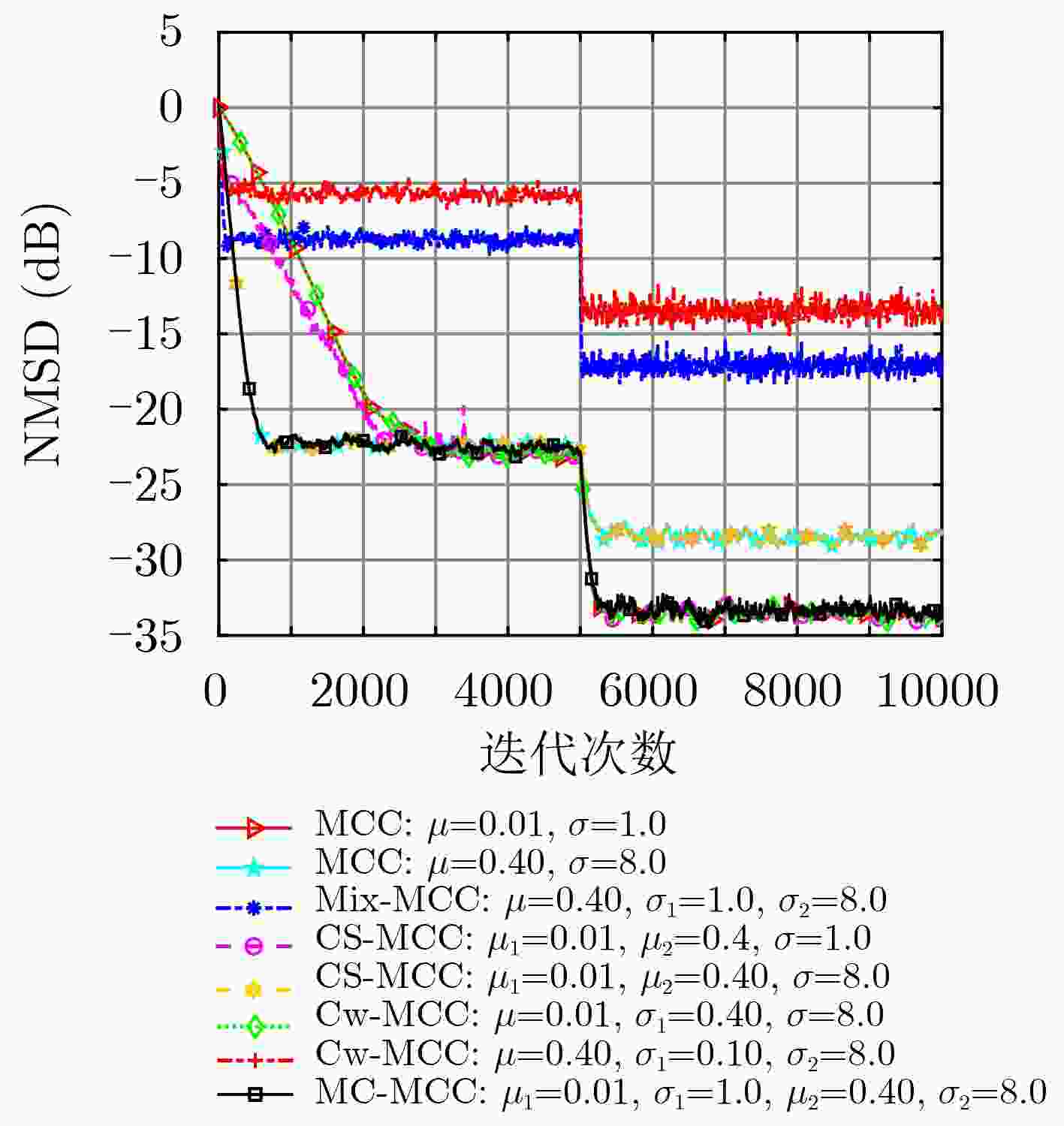
名称 ${\mu _1}$ ${\mu _2}$ ${\sigma _1}$ ${\sigma _2}$

数值 0.01 0.4 1.0 8.0

下载: 导出CSV

参考文献(23)

PRINCIPE J C. Information Theoretic Learning: Renyi’s Entropy and Kernel Perspectives[M]. New York: Springer, 2010: 385–388, 415–424.

CHEN Badong, ZHU Yu, HU Jinchun, et al. System Parameter Identification: Information Criteria and Algorithms[M]. London: Elsevier, 2013: 32–40.

HE Ran, ZHENG Weishi, and HU Baogang. Maximum correntropy criterion for robust face recognition[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2011, 33(8): 1561–1576. doi: 10.1109/TPAMI.2010.220

SINGH A and PRÍNCIPE J C. A loss function for classification based on a robust similarity metric[C]. 2010 International Joint Conference on Neural Networks, Barcelona, Spain, 2010: 1–6.

ZHAO Songlin, CHEN Badong, and PRÍNCIPE J C. An adaptive kernel width update for correntropy[C]. 2012 International Joint Conference on Neural Networks, Brisbane, Australia, 2012: 1–5.

CHEN Badong and PRINCIPE J C. Maximum correntropy estimation is a smoothed MAP estimation[J]. IEEE Signal Processing Letters, 2012, 19(8): 491–494. doi: 10.1109/LSP.2012.2204435

CHEN Badong, XING Lei, LIANG Junli, et al. Steady-state mean-square error analysis for adaptive filtering under the maximum correntropy criterion[J]. IEEE Signal Processing Letters, 2014, 21(7): 880–884. doi: 10.1109/LSP.2014.2319308

SAYED A H. Adaptive Filters[M]. Hoboken: John Wiley & Sons, Inc., 2008: 163–200.

WIDROW B and STEARNS S D. Adaptive Signal Processing[M]. Englewood Cliffs: Prentice-Hall, 1985.

邱天爽. 相关熵与循环相关熵信号处理研究进展[J]. 电子与信息学报, 2020, 42(1): 105–118. doi: 10.11999/JEIT190646

QIU Tianshuang. Development in signal processing based on correntropy and cyclic correntropy[J]. Journal of Electronics &Information Technology, 2020, 42(1): 105–118. doi: 10.11999/JEIT190646

ZHIDKOV S V. Impulsive noise suppression in OFDM-based communication systems[J]. IEEE Transactions on Consumer Electronics, 2003, 49(4): 944–948. doi: 10.1109/TCE.2003.1261179

WANG Ren, CHEN Badong, ZHENG Nanning, et al. A variable step-size adaptive algorithm under maximum correntropy criterion[C]. 2015 International Joint Conference on Neural Networks, Killarney, Ireland, 2015: 1–5.

ZHAO Haiquan, LIU Bing, and SONG Pucha. Variable step-size affine projection maximum correntropy criterion adaptive filter with correntropy induced metric for sparse system identification[J]. IEEE Transactions on Circuits and Systems II: Express Briefs, 2020, 67(11): 2782–2786. doi: 10.1109/TCSII.2020.2973764

WANG Weihua, ZHAO Jihong, QU Hua, et al. An adaptive kernel width update method of correntropy for channel estimation[C]. 2015 IEEE International Conference on Digital Signal Processing, Singapore, 2015: 916–920.

HUANG Fuyi, ZHANG Jiashu, and ZHANG Sheng. Adaptive filtering under a variable kernel width maximum correntropy criterion[J]. IEEE Transactions on Circuits and Systems II: Express Briefs, 2017, 64(10): 1247–1251. doi: 10.1109/TCSII.2017.2671339

李群生, 赵剡, 寇磊, 等. 一种基于多尺度核学习的仿射投影滤波算法[J]. 电子与信息学报, 2020, 42(4): 924–931. doi: 10.11999/JEIT190023

LI Qunsheng, ZHAO Yan, KOU Lei, et al. An affine projection algorithm with multi-scale kernels learning[J]. Journal of Electronics &Information Technology, 2020, 42(4): 924–931. doi: 10.11999/JEIT190023

CHEN Badong, WANG Xin, LU Na, et al. Mixture correntropy for robust learning[J]. Pattern Recognition, 2018, 79: 318–327. doi: 10.1016/j.patcog.2018.02.010

ARENAS-GARCÍA J, GÓMEZ-VERDEJO V, and FIGUEIRAS-VIDAL A R. New algorithms for improved adaptive convex combination of LMS transversal filters[J]. IEEE Transactions on Instrumentation and Measurement, 2005, 54(6): 2239–2249. doi: 10.1109/TIM.2005.858823

SILVA M T M and NASCIMENTO V H. Improving the tracking capability of adaptive filters via convex combination[J]. IEEE Transactions on Signal Processing, 2008, 56(7): 3137–3149. doi: 10.1109/TSP.2008.919105

ARENAS-GARCIA J, FIGUEIRAS-VIDAL A R, and SAYED A H. Mean-square performance of a convex combination of two adaptive filters[J]. IEEE Transactions on Signal Processing, 2006, 54(3): 1078–1090. doi: 10.1109/TSP.2005.863126

SHI Liming and LIN Yun. Convex combination of adaptive filters under the maximum correntropy criterion in impulsive interference[J]. IEEE Signal Processing Letters, 2014, 21(11): 1385–1388. doi: 10.1109/LSP.2014.2337899

ARENAS-GARCIA J, MARTINEZ-RAMON M, GOMEZ-VERDEJO V, et al. Multiple plant identifier via adaptive LMS convex combination[C]. 2003 IEEE International Symposium on Intelligent Signal Processing, Budapest, Hungary, 2003: 137–142.

MA Wentao, QU Hua, GUI Guan, et al. Maximum correntropy criterion based sparse adaptive filtering algorithms for robust channel estimation under non-Gaussian environments[J]. Journal of the Franklin Institute, 2015, 352(7): 2708–2727. doi: 10.1016/j.jfranklin.2015.03.039

施引文献

期刊类型引用(21)

1.	李民，郭琳，姚雄. 优化高斯过程回归在太阳能集热效率预测上的应用. 电网与清洁能源. 2023(08): 127-131+138 . 百度学术
2.	Han-shan Li. Recognition model and algorithm of projectiles by combining particle swarm optimization support vector and spatial-temporal constrain. Defence Technology. 2023(09): 273-283 . 必应学术
3.	何旭，席佩瑶，辛云宏. 基于代价敏感思想和自适应增强集成的SVM多分类算法. 微型电脑应用. 2023(09): 1-3 . 百度学术
4.	徐红先，张书玮. 基于极限学习机及多姿态信息融合的步态识别. 机械. 2023(11): 72-80 . 百度学术
5.	陈晓禾，曹旭刚，陈健生，胡春华，马羽. 基于三维卷积的帕金森患者拖步识别. 电子与信息学报. 2021(12): 3467-3475 . 本站查看
6.	雷建超，刘栋博，房玉，庄祖江，刘俊豪. 基于表面肌电信号的性别差异性手势识别. 中国医学物理学杂志. 2020(03): 337-341 . 百度学术
7.	金鑫，冯毅，尤雪汐，王佳欣. 基于机器学习的信息安全设备调配保障技术研究. 电子科技. 2020(08): 80-86 . 百度学术
8.	孟明，闫冉，高云园，佘青山. 基于多元变分模态分解的脑电多域特征提取方法. 传感技术学报. 2020(06): 853-860 . 百度学术
9.	王志芳，王书涛，王贵川. 粒子群优化BP神经网络在甲烷检测中的应用. 光子学报. 2019(04): 147-154 . 百度学术
10.	邹倩颖，王小芳. 粒子群优化BP神经网络在步态识别中的研究. 实验技术与管理. 2019(08): 130-133+138 . 百度学术
11.	郭海山，高波涌，陆慧娟. 基于Boruta-PSO-SVM的股票收益率研究. 传感器与微系统. 2018(03): 51-53+57 . 百度学术
12.	周长林，钱志升，王勤民，余道杰，程俊平. 基于PSO-SVM方法的电源线传导泄漏信号识别与还原. 电子与信息学报. 2018(09): 2206-2211 . 本站查看
13.	赵荣建，汤敏芳，陈贤祥，杜利东，曾华林，赵湛，方震. 基于光纤传感的生理参数监测系统研究. 电子与信息学报. 2018(09): 2182-2189 . 本站查看
14.	胡长俊，袁树杰. 煤矿井下WSN中基于自适应粒子群聚类算法的多sink节点部署. 计算机科学. 2018(11): 103-107+123 . 百度学术
15.	王秀娟，相从斌. 基于累积量的DoS攻击检测算法. 北京工业大学学报. 2017(09): 1328-1334 . 百度学术
16.	杜必强，孙立江. 基于PSO-SVM模型的焊接转子环焊缝超声缺陷识别. 动力工程学报. 2017(05): 379-385 . 百度学术
17.	赵湛，韩璐，方震，陈贤祥，杜利东，刘正奎. 基于可穿戴设备的日常压力状态评估研究. 电子与信息学报. 2017(11): 2669-2676 . 本站查看
18.	董广宇. 基于多特征融合的复杂路况步态识别方法. 科学技术与工程. 2017(08): 202-207 . 百度学术
19.	韩笑，佘青山，高云园，罗志增. 基于NA-MEMD和互信息的脑电特征提取方法. 传感技术学报. 2016(08): 1140-1148 . 百度学术
20.	黄成泉，王士同，蒋亦樟，董爱美. v-软间隔罗杰斯特回归分类机. 电子与信息学报. 2016(04): 985-992 . 本站查看
21.	徐超立，林科，杨晨，吴超华，高小榕. 基于小腿表面肌电的智能机器人协同控制方法. 中国生物医学工程学报. 2016(04): 385-393 . 百度学术

其他类型引用(43)

资源附件(0)

访问统计

图(6) / 表(2)

计量

文章访问数: 1513
HTML全文浏览量: 1212
PDF下载量: 183
被引次数: 64

姓名
邮箱
手机号码
标题
留言内容
验证码

留言板

最大互相关熵多凸组合自适应滤波算法

doi: 10.11999/JEIT200288

通讯作者:
陈霸东　chenbd@mail.xjtu.edu.cn

计量

Convex Combination of Multiple Adaptive Filters under the Maximum Correntropy Criterion

期刊类型引用(21)

其他类型引用(43)

计量

目录

名称	${\mu _1}$ / ${\sigma _1}$	${\mu _2}$ / ${\sigma _2}$	${\mu _3}$ / ${\sigma _3}$	${\mu _4}$ / ${\sigma _4}$	${\mu _\xi }$ / ${\sigma _\xi }$
数值	0.03/6.0	0.04/4.0	0.08/2.0	0.3/1.5	4.5/1.0

名称	${\mu _1}$	${\mu _2}$	${\sigma _1}$	${\sigma _2}$
数值	0.01	0.4	1.0	8.0

留言板

最大互相关熵多凸组合自适应滤波算法

doi: 10.11999/JEIT200288

通讯作者: 陈霸东 chenbd@mail.xjtu.edu.cn

计量

出版历程

Convex Combination of Multiple Adaptive Filters under the Maximum Correntropy Criterion

期刊类型引用(21)

其他类型引用(43)

计量

出版历程

目录

通讯作者:
陈霸东　chenbd@mail.xjtu.edu.cn