A Three-Dimensional Imaging Algorithm of Downward-looking Sparse Linear Array SAR Based on Low-rank Tensor
-
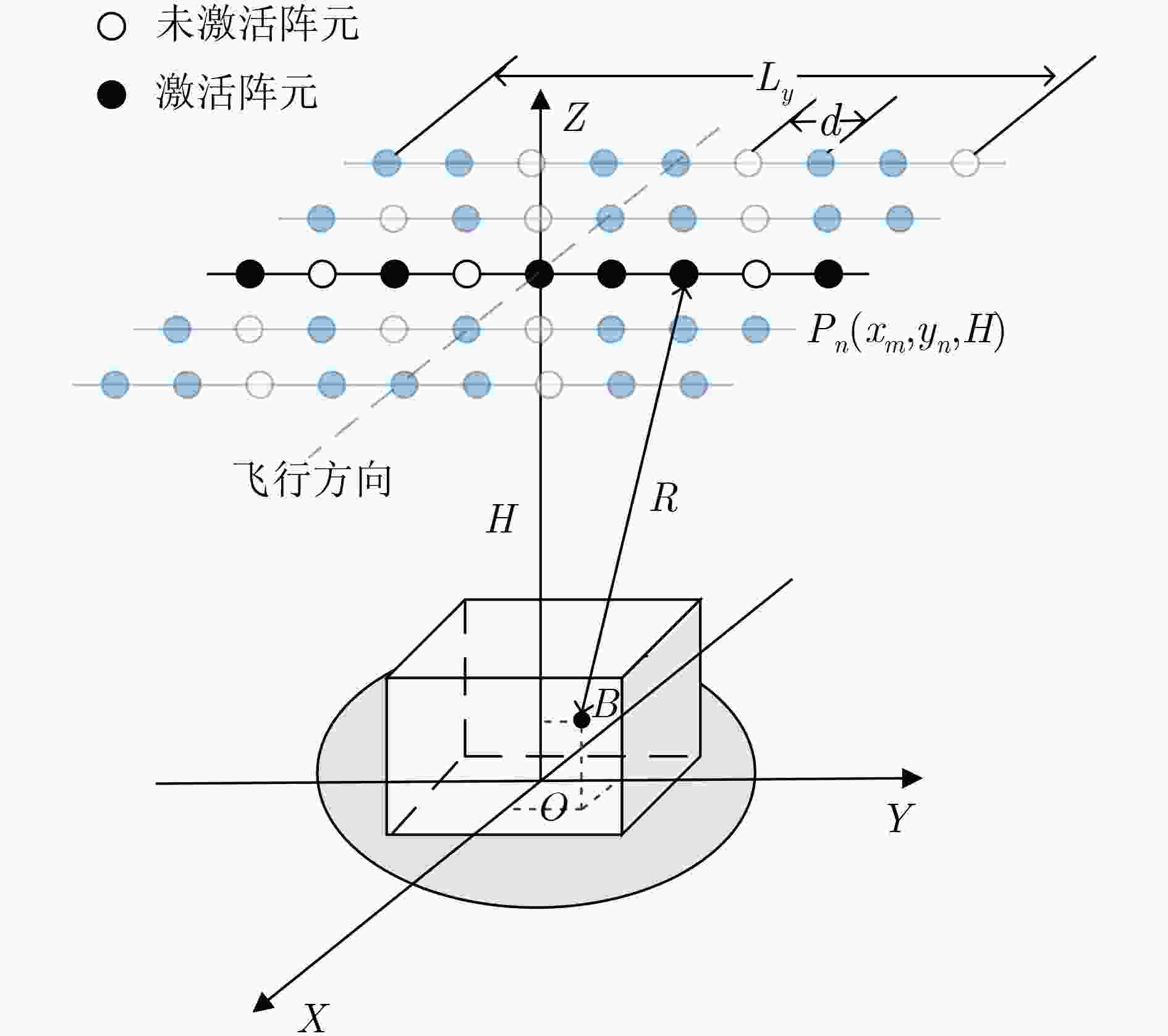
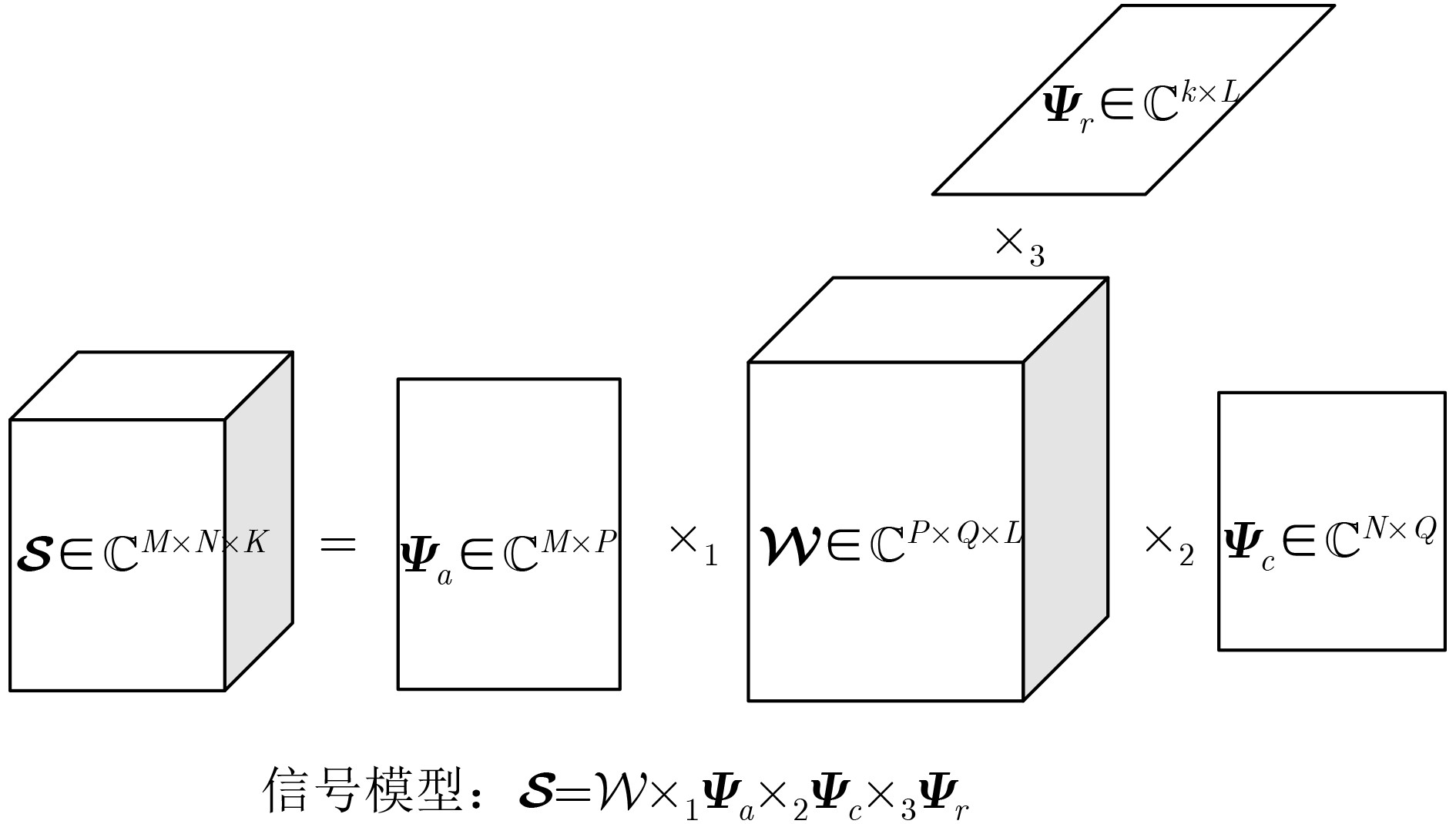
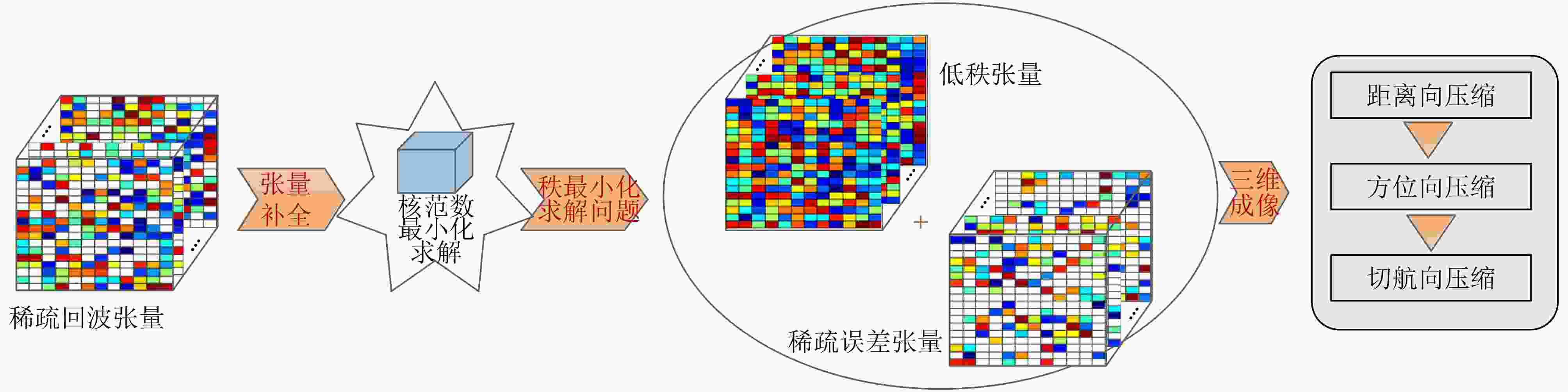
摘要: 为了解决3维稀疏数据处理中向量化或矩阵化带来的原始空间结构破坏与计算复杂度高的问题,该文针对下视稀疏线阵3维SAR成像几何模型和回波信号特点,构建了张量空间信号模型,提出了一种基于低秩张量补全的3维SAR稀疏成像算法。该算法首先利用回波张量的低秩性,通过张量补全重构稀疏回波中的丢失元素,再对补全后的全采样信号张量进行3维成像,从而获得高效率、低旁瓣、高分辨率3维图像。基于X波段下视稀疏线阵3维SAR点目标回波进行了3维成像仿真实验,比较了在不同信噪比和采样率条件下的成像性能,并基于实测数据进一步验证了该算法的有效性和优势。Abstract: In order to solving the problems of the inner structure damage and the high computation load brought by the vectorizing or matrixing of 3-D sparse data, the 3-D signal model is established in tensor space for downward-looking sparse linear array three-dimensional SAR. Based on this signal model, a three-dimensional SAR sparse imaging algorithm is proposed in this paper. The missing data firstly can be recovered by tensor completion on the assumption that the echo tensor is essentially low rank. Then, the resulting 3-D images can be well focused by any Fourier transform-based 3-D imaging algorithms with the recovered full-sampled data tensor. The proposed algorithm achieves not only high resolution and low-level side-lobes but also the ideal computational cost and memory consumption, which verified by several numerical simulations and multiple comparative studies on real data.
-
表 1 基于低秩张量补全的下视稀疏线阵3维SAR成像算法流程
输入:稀疏回波信号张量${{{\cal S}}}$,采样集$\varOmega $,正则参数$\rho $,最大迭代次数$J$ 输出:3维图像${{{\cal I}}}$ 初始化:${ {{{\cal X}}}_\varOmega } = { {{{\cal S}}}_\Omega }$, ${ {{{\cal Y}}}_i} = 0$, ${ {{{\cal M}}}_i} = {{{\cal X}}}$, ${\rho ^0} \ge 1$ //步骤 1 张量补全稀疏回波信号 (1) for j = 0 to J do (2) for i = 1 to 3 do (3) 更新${{ {\cal M} } }_i^{j + 1} \!=\! {\rm{fol} }{ {\rm{d} }_i}\left( { {{ {\cal M} } }_{i(i)}^{j + 1} } \right) \!=\! {\rm{fol} }{ {\rm{d} }_i}\left[ { {D_{ { { {\alpha _i} } / { {\rho ^j} } } } }({ {{ {\cal X} } }_{(i)} } + 1/{\rho ^j}{ {{ {\cal Y} } }_{i(i)} })} \right]$,其中fold表示将矩阵表示为对应阶的张量,${D_{{{{\alpha _i}} / {{\rho ^j}}}}}$表示
$\tau = {{{\alpha _i}} / {{\rho ^j}}}$时的软阈值因子${D_\tau }$。(4) end for
(5) 更新${{ {\cal X} } }_\varOmega ^{j + 1} = 1/3{\left(\displaystyle\sum\limits_{i = 1}^3 { {{ {\cal M} } }_i^{j + 1} } - 1/{\rho ^j}{{ {\cal Y} } }_i^{j + 1}\right)_\varOmega }$(6) 更新拉格朗日算子${{ {\cal Y} } }_i^{j + 1} = {{ {\cal Y} } }_i^j + {\rho ^j}({ {{ {\cal X} } }^{j + 1} } - {{ {\cal M} } }_i^{j + 1})$ (7) 更新${\rho ^{j{\rm{ + }}1}} = {t}{\rho ^j},{t} \in [1.1,1.2]$ (8) end for //步骤 2 3维RD处理 (9) ${{ {\cal I} } } = {\rm{3D {\text{-}} RD(} }{{ {\cal X} } })$,其中3D-RD表示3维距离徙动校正(Range Doppler, RD)处理,见参考文献[16]。 表 2 仿真系统参数
参数 数值 中心频率 10 GHz 信号带宽 150 MHz 飞行高度 2000 m 飞行速度 200 m/s 脉冲重复频率 1000 Hz 线阵长度 6 m 方位向全采样数 200 切航向全采样数 120 表 3 基于80%采样率稀疏数据的点目标的3维成像性能
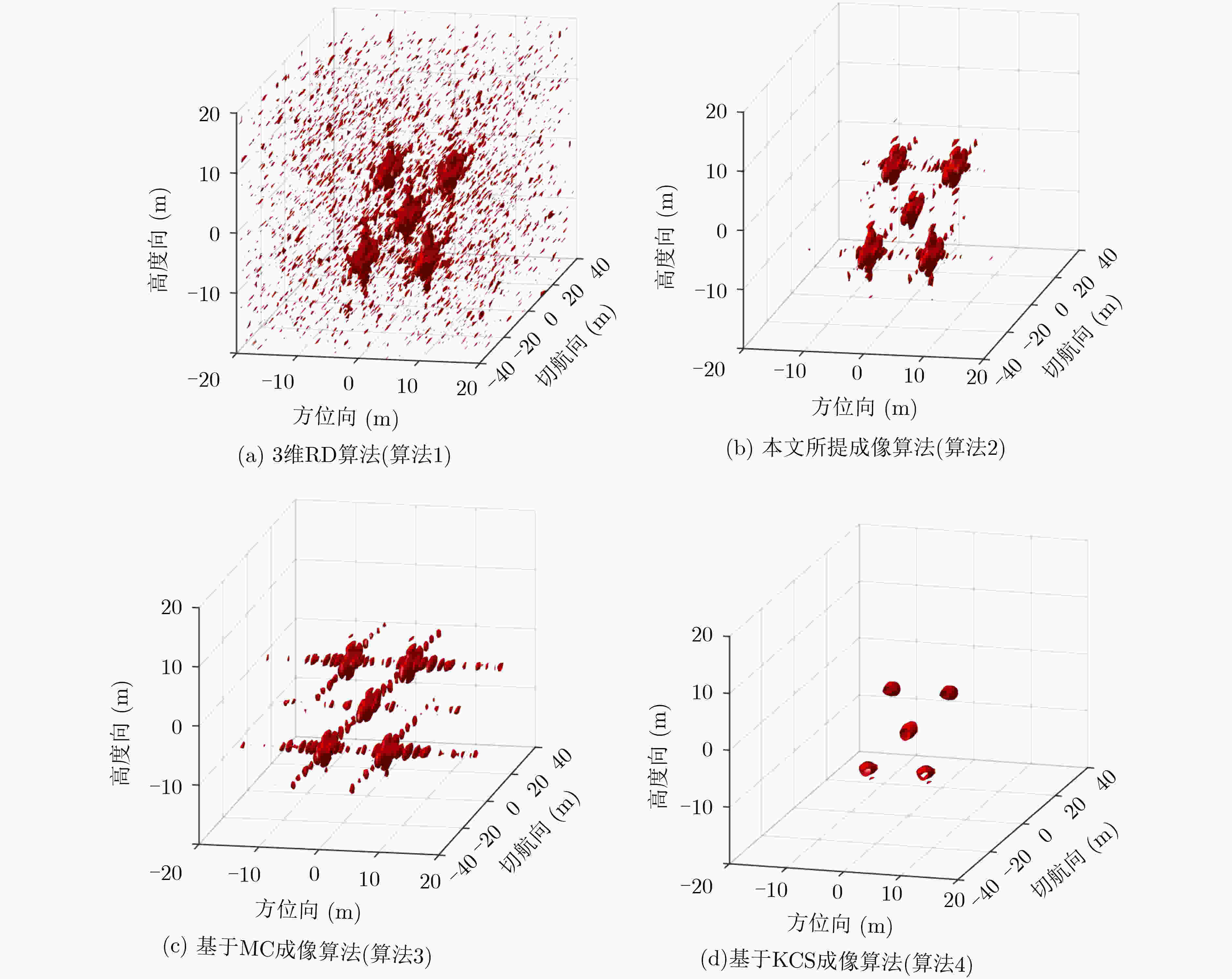
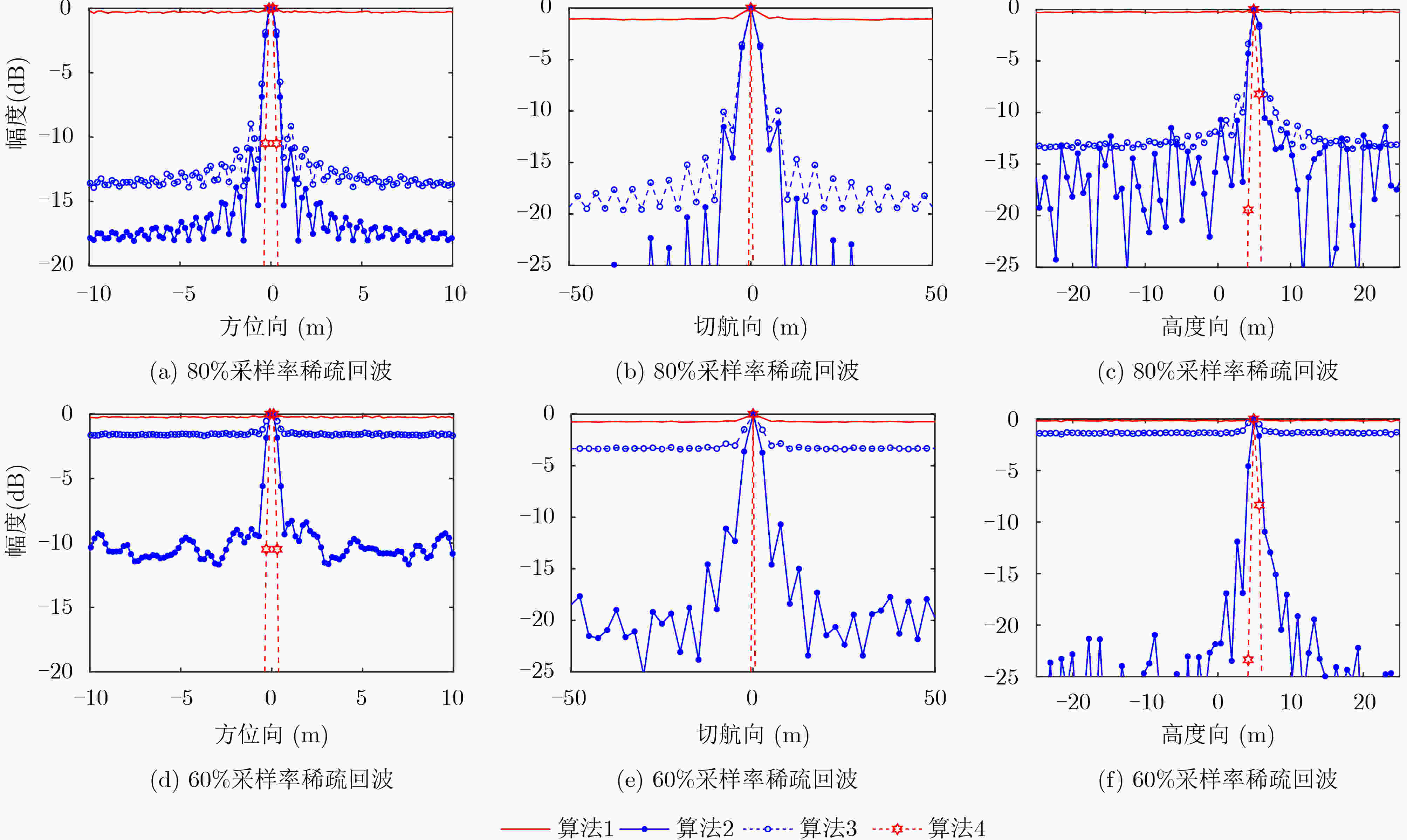
成像算法 峰值旁瓣比 积分旁瓣比 80%采样 60%采样 80%采样 60%采样 方位向 算法1 –0.94 –0.57 –0.21 –0.09 算法2 –10.69 –10.90 –1.79 –1.44 算法3 –10.03 –2.77 –0.94 –0.13 切航向 算法1 –0.16 –0.16 –0.10 –0.18 算法2 –8.33 –12.03 –3.59 –3.19 算法3 –9.19 –1.44 –2.45 –0.21 高度向 算法1 –0.19 –0.11 –0.31 –0.38 算法2 –16.69 –13.41 –7.11 –5.97 算法3 –11.57 –1.33 –1.96 –0.49 表 4 下视线阵3维SAR系统参数
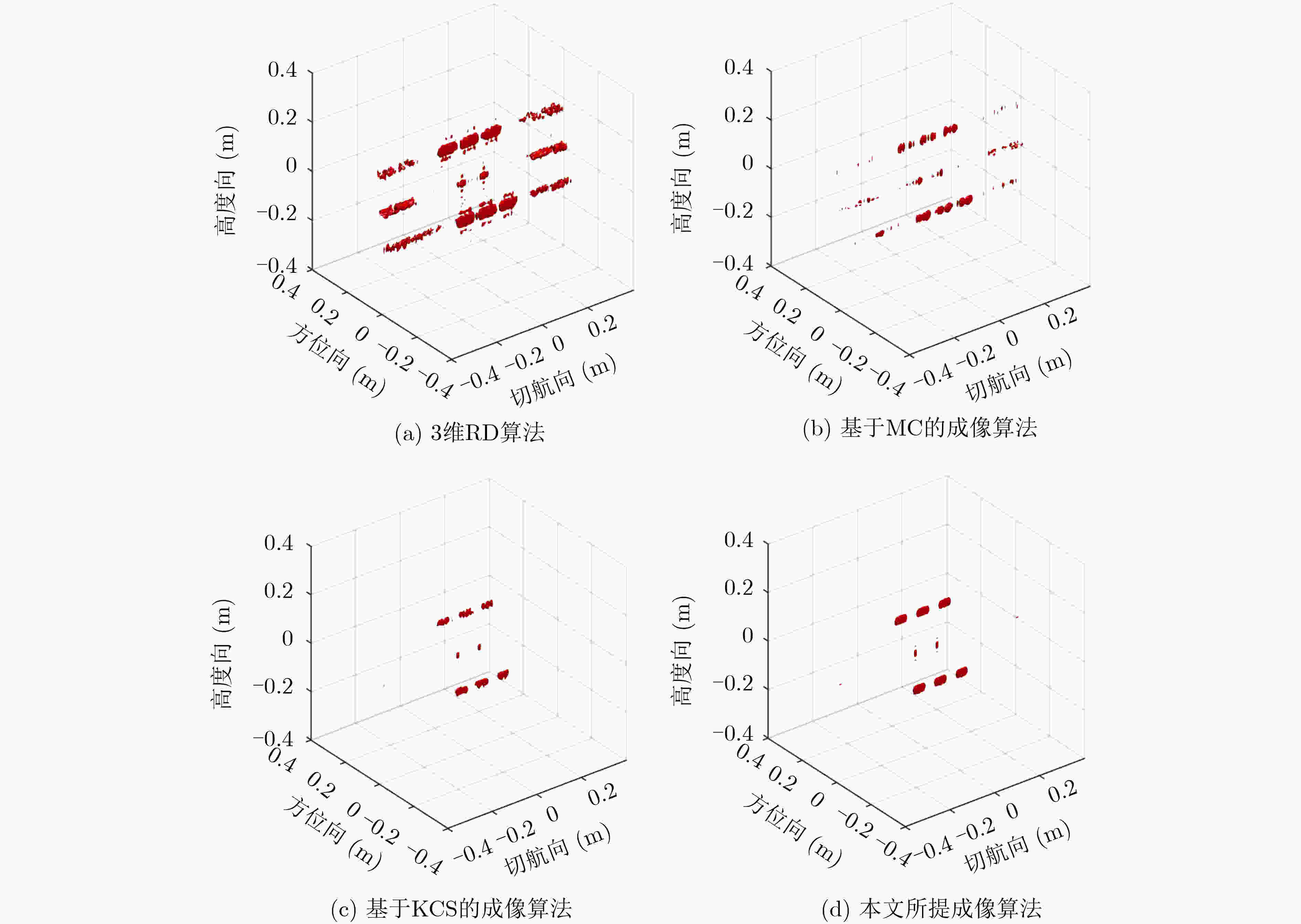
参数 数值 中心载频 10 GHz 带宽 4 GHz 频率步进 1 MHz 高度 2.2 m 切航向全采样扫描点数 50 切航向全采样扫描间隔 0.02 m 方位向全采样扫描点数 160 方位向全采样扫描间隔 0.01 m -
[1] GIERULL C H. On a concept for an airborne downward-looking imaging radar[J]. International Journal of Electronics and Communications, 1999, 53(6): 295–304. [2] 彭学明, 王彦平, 谭维贤, 等. 基于跨航向稀疏阵列的机载下视MIMO 3D-SAR三维成像算法[J]. 电子与信息学报, 2012, 34(4): 943–949. doi: 10.3724/SP.J.1146.2011.00720PENG Xueming, WANG Yanping, TAN Weixian, et al. Airborne downward-looking MIMO 3D-SAR imaging algorithm based on cross-track thinned array[J]. Journal of Electronics &Information Technology, 2012, 34(4): 943–949. doi: 10.3724/SP.J.1146.2011.00720 [3] 韩冬, 周良将, 焦泽坤, 等. 基于改进三维后向投影的多圈圆迹SAR相干三维成像方法[J]. 电子与信息学报, 2021, 43(1): 131–137. doi: 10.11999/JEIT190945HAN Dong, ZHOU Liangjiang, JIAO Zekun, et al. A coherent 3-D imaging method for multi-circular SAR based on an improved 3-D back projection algorithm[J]. Journal of Electronics &Information Technology, 2021, 43(1): 131–137. doi: 10.11999/JEIT190945 [4] PENG Xueming, HONG Wen, WANG Yanping, et al. Polar format imaging algorithm with wave-front curvature phase error compensation for airborne DLSLA three-dimensional SAR[J]. IEEE Geoscience and Remote Sensing Letters, 2014, 11(6): 1036–1040. doi: 10.1109/LGRS.2013.2282335 [5] 成晨. 三维合成孔径雷达超分辨成像方法研究[D].[硕士论文]. 电子科技大学, 2012.CHENG Chen. Research on superresolution imaging method for three-dimensional SAR[D].[Master dissertation], University of Electronic Science and Technology of China, 2012. [6] ZHANG Siqian, ZHU Yutao, and KUANG Gangyao. Imaging of downward-looking linear array three-dimensional SAR based on FFT-MUSIC[J]. IEEE Geoscience and Remote Sensing Letters, 2015, 12(4): 885–889. doi: 10.1109/LGRS.2014.2365611 [7] 王洪雁, 于若男. 基于稀疏和低秩恢复的稳健DOA估计方法[J]. 电子与信息学报, 2020, 42(3): 589–596. doi: 10.11999/JEIT190263WANG Hongyan and YU Ruonan. Sparse and low rank recovery based robust DOA estimation method[J]. Journal of Electronics &Information Technology, 2020, 42(3): 589–596. doi: 10.11999/JEIT190263 [8] ZHANG Siqian, DONG Ganggang, and KUANG Gangyao. Superresolution downward-looking linear array three-dimensional SAR imaging based on two-dimensional compressive sensing[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2016, 9(6): 2184–2196. doi: 10.1109/JSTARS.2016.2549548 [9] ZHANG Siqian, DONG Ganggang, and KUANG Gangyao. Matrix completion for downward-looking 3-D SAR imaging with a random sparse linear array[J]. IEEE Transactions on Geoscience and Remote Sensing, 2018, 56(4): 1994–2006. doi: 10.1109/TGRS.2017.2771826 [10] KOLDA T G and BADER B W. Tensor decompositions and applications[J]. SIAM Review, 2009, 51(3): 455–500. doi: 10.1137/07070111X [11] DAI Junwen and JIN Yaqiu. Scattering simulation and reconstruction of a 3-D complex target using downward-looking step-frequency radar[J]. IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(10): 4035–4047. doi: 10.1109/TGRS.2011.2131659 [12] 张澄波. 综合孔径雷达—原理、系统分析与应用[M]. 北京: 科学出版社, 1989: 39–40.ZHANG Chengbo. Synthetic Aperture Radar - Principle, System Analysis and Application[M]. Beijing: Science Press, 1989: 39–40. [13] 戴俊文, 金亚秋, 徐丰. 复杂目标电磁散射仿真与频率步进雷达对三维目标的重构[J]. 中国科学: 信息科学, 2011, 41(8): 912–928.DAI Junwen, JIN Yaqiu, and XU Feng. Scattering simulation and reconstruction of a 3D complex target using downward-looking step-frequency radar[J]. SCIENTIA SINICA Informationis, 2011, 41(8): 912–928. [14] LIU Ji, MUSIALSKI P, WONKA P, et al. Tensor completion for estimating missing values in visual data[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2013, 35(1): 208–220. doi: 10.1109/TPAMI.2012.39 [15] DING Shanshan, TONG Ningning, ZHANG Yongshun, et al. Super-resolution 3D imaging in MIMO radar using spectrum estimation theory[J]. IET Radar, Sonar & Navigation, 2017, 11(2): 304–312. doi: 10.1049/iet-rsn.2016.0233 [16] 张思乾. 下视线阵三维SAR成像技术研究[D]. [博士论文]. 国防科学技术大学, 2016.ZHANG Siqian. Research on downward-looking linear array three-dimensional SAR imaging technology[D]. [Ph.D. dissertation], National University of Defense Technology, 2016. [17] DUARTE M F and BARANIUK R G. Kronecker compressive sensing[J]. IEEE Transactions on Image Processing, 2012, 21(2): 494–504. doi: 10.1109/TIP.2011.2165289 -





 下载:
下载:



 下载:
下载:
