Time-Offset Generalized Frequency Division Multiplexing Communication in Doubly-selective Channels
-
摘要: 当信道存在时间-频率双选择性时,严重的子载波间干扰和子符号间干扰将导致广义频分复用(GFDM)系统性能显著下降。为此,该文提出一种时间偏移GFDM系统(TO-GFDM),通过对传统GFDM系统的原型滤波器进行时间偏移,来提高双选择信道下GFDM系统的性能。该文推导了GFDM信号在双选择信道中的平均信干比公式,并提出基于离散导频的联合迭代信道估计与符号检测算法,该算法利用信道估计器与串行干扰消除符号检测器之间的信息交换,逐步减小干扰信号,提高信道估计与符号检测的精度。理论分析与仿真实验结果表明,在双选择信道条件下,时间偏移GFDM比传统的GFDM具有更高的平均信干比和误码率性能;并且,联合迭代信道估计与符号检测算法能有效降低系统误码率。Abstract: The performance of Generalized Frequency Division Multiplexing (GFDM) systems significantly degrades over time-frequency doubly selective channels due to the severe inter-carrier interference and inter-subsymbol interference. To this end, a Time-Offset GFDM (TO-GFDM) is proposed, which can improve the performance of GFDM systems under doubly selective channel environment by introducing a time-offset to the prototype filter of conventional GFDM systems. The average signal-to-interference ratio of GFDM systems in doubly selective channels is analytically derived, and a pilot-aided joint iterative channel estimation and symbol detection algorithm is proposed. The proposed algorithm can progressively decrease the interference signal and improve the performance of channel estimation and symbol detection with the information exchanging between the channel estimation unit and the successive interference cancellation based symbol detection unit. The results of theoretical analysis and simulation demonstrate that in doubly selective channels, the time-offset GFDM outperforms the conventional GFDM in terms of average signal-to-interference ratio and bit error rate, and the joint iterative channel estimation and symbol detection algorithm can reduce the bit error rate effectively.
-
表 1 迭代联合信道估计与符号检测算法
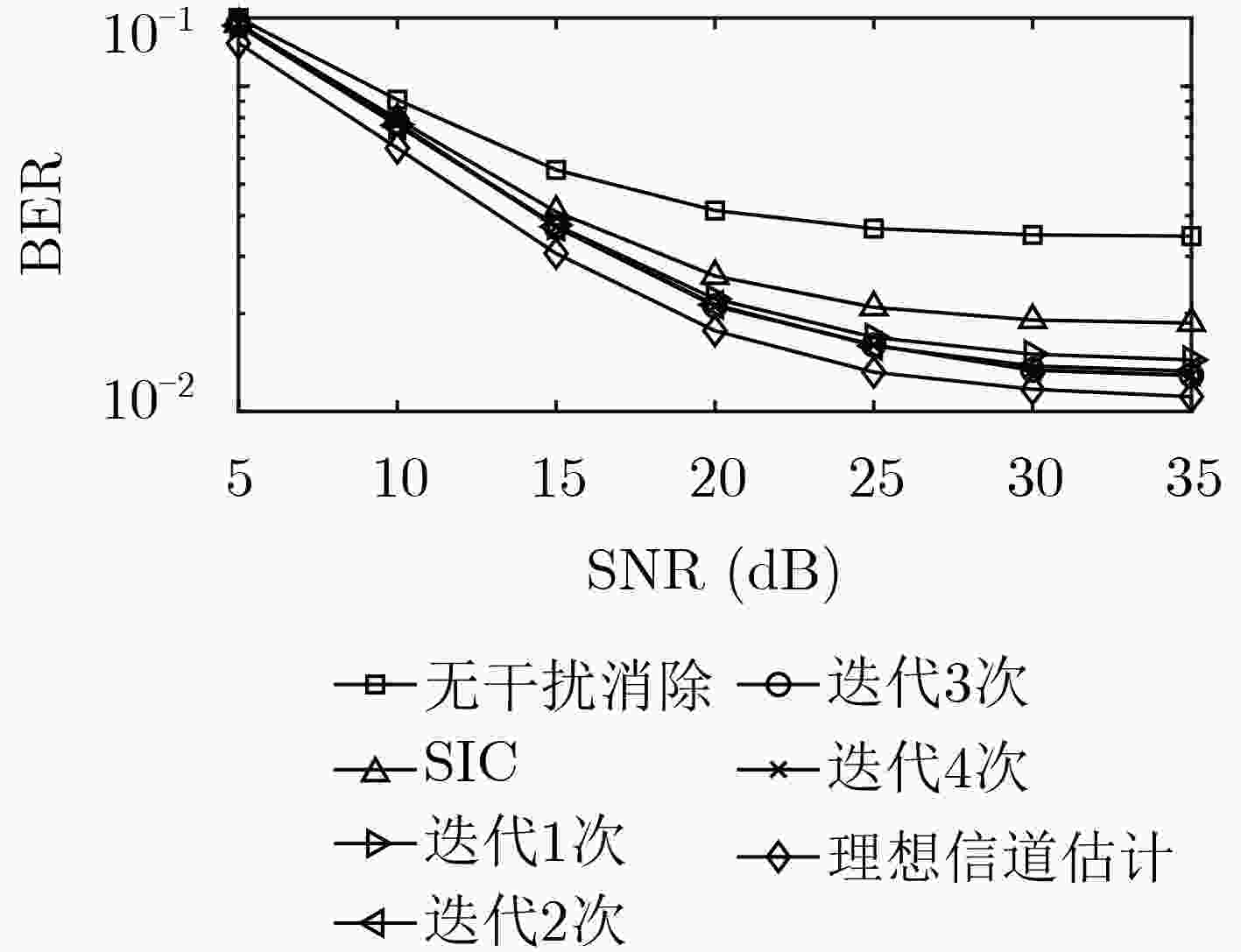
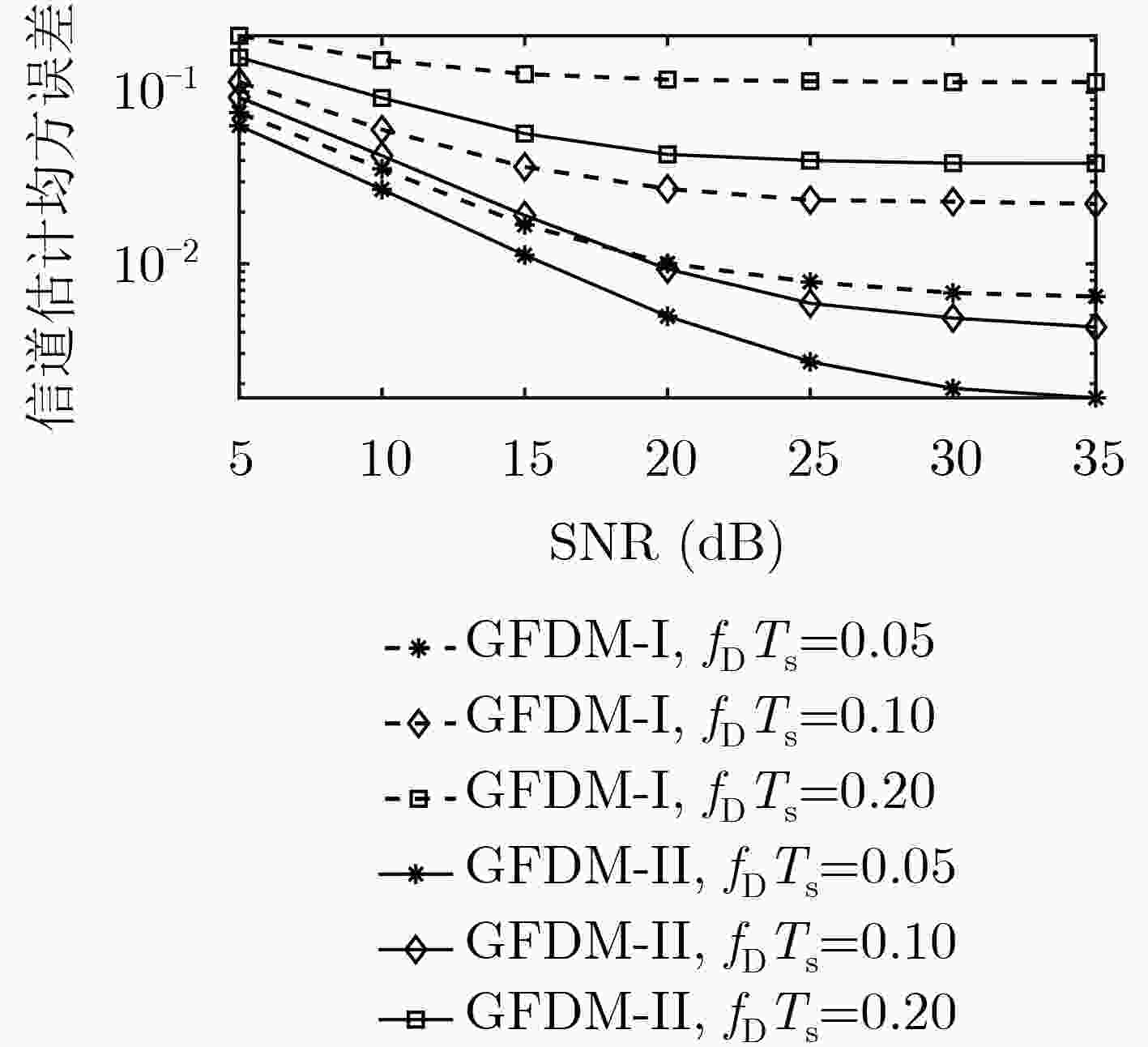
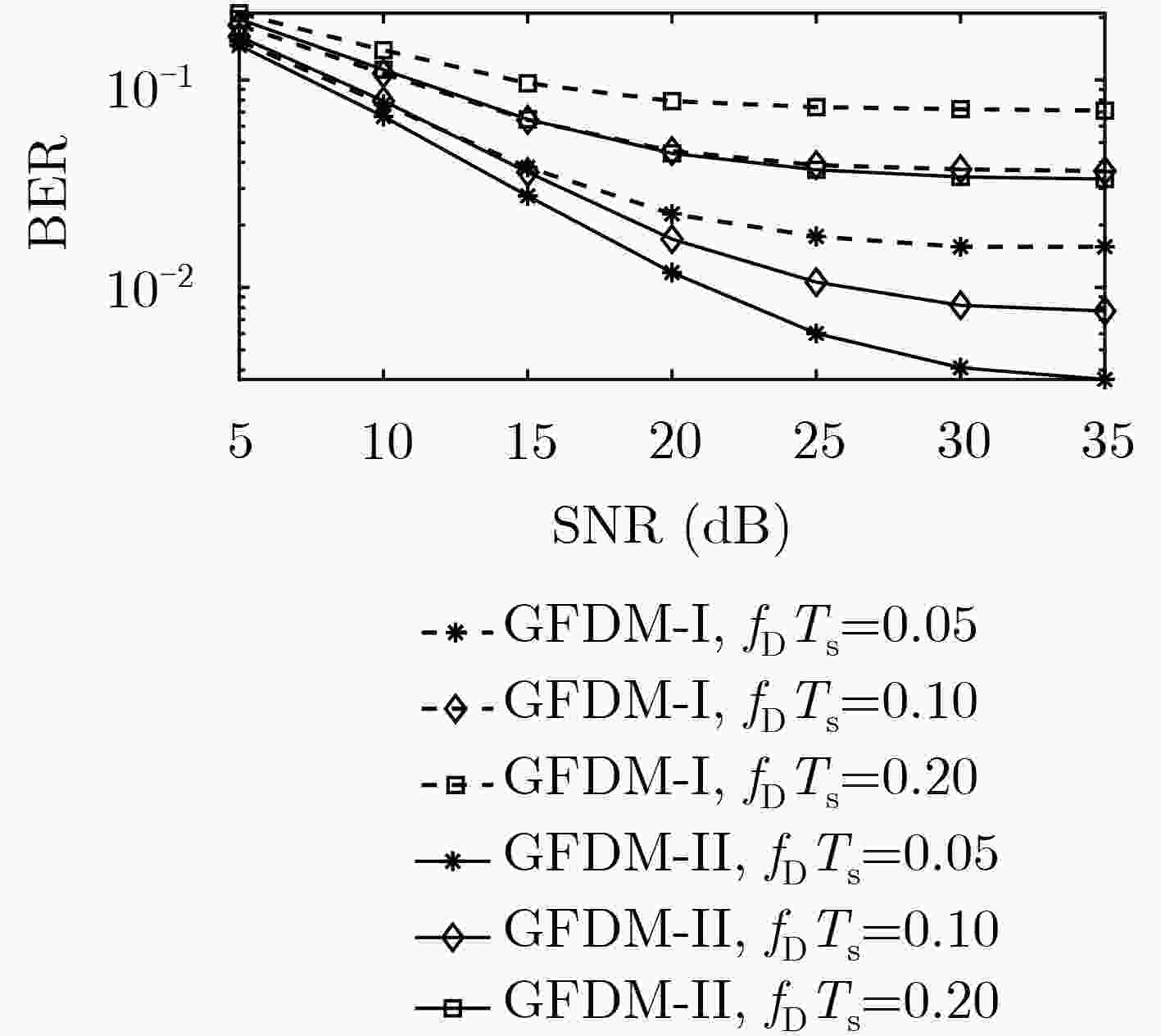
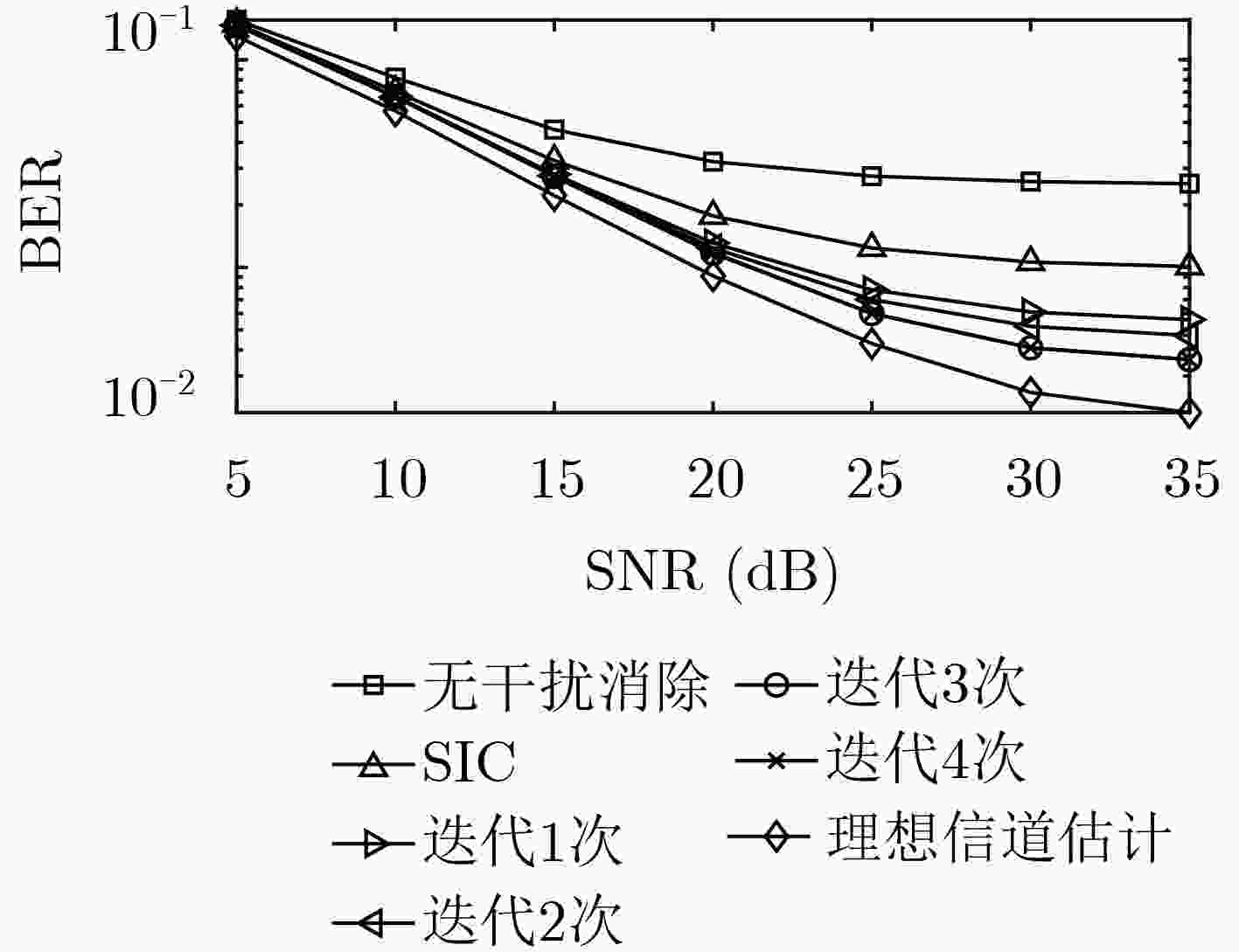
(1) 令迭代次数指示变量$i = 0$; (2) 通过式(20)计算得到符号判决统计量${{{r}}^{(i)}}$; (3) 利用式(23)估计导频符号的广义信道矢量${\tilde{ h}}_{\rm{P}}^{{\rm{LS}}(i)}$; (4) 基于${\tilde{ h}}_{\rm{P}}^{{\rm{LS}}(i)}$,利用式(25)估计广义信道矩阵${{\tilde {\mathbb {H}}}^{(i)}}$; (5) $i = i + 1$; (6) 利用式(36)消除导频符号对数据符号的干扰,即${{{r}}^{(i)}} = {{{r}}^{(0)}} - {{\tilde {\mathbb {H}}}^{(i - 1)}}{{{d}}_{\rm{p}}}$; (7) 利用式(37)确定最佳检测符号的索引值$({k^ * },{m^ * })$,并基于${{{{({r_{{k^ * },{m^ * }}})}^{(i)}}}/{{{(\tilde H_{{k^ * },{m^ * }}^{0,0})}^{(i - 1)}}}}$的值进行硬判决,得到估计值${({\tilde d_{{k^ * },{m^ * }}})^{(i)}}$; (8) 对符号判决统计量${{{r}}^{(i)}}$进行更新,${ {{r} }^{(i)} } = { {{r} }^{(i)} } - {[{\tilde {{H} }^{(i - 1)} }]_{ {k^ * } + {m^ * }K} }{({\tilde d_{ {k^ * },{m^ * } } })^{(i)} }$; (9) 返回第(7)步,对剩余未处理的数据符号依次完成硬判决; (10) 更新判决统计量,${{{r}}^{(i)}} = {{{r}}^{(0)}} - {{\tilde {\mathbb {H'}}}^{(i - 1)}}({\tilde{ d}}_{\rm{d}}^{(i)} + {{{d}}_{\rm{p}}})$; (11) 返回第(3)步,直至到达设定的迭代次数或者收敛。 表 2 系统仿真参数设定
参数 参数值 子载波数目 32 原型滤波器 升余弦函数 滚降因子$\alpha $ 0.4 采样频率 4.8 MHz 调制方式 QPSK 信道功率延迟分布 [0, –1, –9, –10, –15, –20] dB 时变信道模型 Jakes $\sigma _{\rm{p}}^2/\sigma _{\rm{d}}^2$ 2 -
MICHAILOW N, MATTHÉ M, GASPAR I S, et al. Generalized frequency division multiplexing for 5th generation cellular networks[J]. IEEE Transactions on Communications, 2014, 62(9): 3045–3061. doi: 10.1109/TCOMM.2014.2345566 TAO Yunzheng, LIU Long, LIU Shang, et al. A survey: Several technologies of non-orthogonal transmission for 5G[J]. China Communications, 2015, 12(10): 1–15. doi: 10.1109/CC.2015.7315054 FETTWEIS G, KRONDORF M, and BITTNER S. GFDM-generalized frequency division multiplexing[C]. The 69th IEEE Vehicular Technology Conference, Barcelona, Spain, 2009: 1–4. LI Fei, ZHENG Kan, LONG Hang, et al. Performance analysis of complementary GFDM in IoT communications[C]. 2019 IEEE 89th Vehicular Technology Conference, Kuala Lumpur, Malaysia, 2019: 1–5. 钱志鸿, 田春生, 郭银景, 等. 智能网联交通系统的关键技术与发展[J]. 电子与信息学报, 2020, 42(1): 2–19. doi: 10.11999/JEIT190787QIAN Zhihong, TIAN Chunsheng, GUO Yinjing, et al. The key technology and development of intelligent and connected transportation system[J]. Journal of Electronics &Information Technology, 2020, 42(1): 2–19. doi: 10.11999/JEIT190787 DE ALMEIDA I B F, MENDES L L, RODRIGUES J J P C, et al. 5G waveforms for IoT applications[J]. IEEE Communications Surveys & Tutorials, 2019, 21(3): 2554–2567. doi: 10.1109/COMST.2019.2910817 LIM B and KO Y C. SIR analysis of OFDM and GFDM waveforms with timing offset, CFO, and phase noise[J]. IEEE Transactions on Wireless Communications, 2017, 16(10): 6979–6990. doi: 10.1109/TWC.2017.2736998 MOHAMMADIAN A, TELLAMBURA C, and VALKAMA M. Analysis of self-interference cancellation under phase noise, CFO, and IQ imbalance in GFDM full-duplex transceivers[J]. IEEE Transactions on Vehicular Technology, 2020, 69(1): 700–713. doi: 10.1109/TVT.2019.2953623 VILAIPORNSAWAI U and JIA Ming. Scattered-pilot channel estimation for GFDM[C]. 2014 IEEE Wireless Communications and Networking Conference, Istanbul, Turkey, 2014: 1053–1058. EHSANFAR S, MATTHE M, ZHANG Dan, et al. Interference-free pilots insertion for MIMO-GFDM channel estimation[C]. 2017 IEEE Wireless Communications and Networking Conference, San Francisco, USA, 2017: 1–6. NA Zhenyu, PAN Zheng, XIONG Mudi, et al. Soft decision control iterative channel estimation for the internet of things in 5G networks[J]. IEEE Internet of Things Journal, 2019, 6(4): 5990–5998. doi: 10.1109/JIOT.2018.2864213 CHENG Hao, XIA Yili, HUANG Yongming, et al. Joint channel estimation and Tx/Rx I/Q imbalance compensation for GFDM systems[J]. IEEE Transactions on Wireless Communications, 2019, 18(2): 1304–1317. doi: 10.1109/TWC.2019.2891649 LI Fei, ZHENG Kan, ZHAO Long, et al. Design and performance of a novel interference-free GFDM transceiver with dual filter[J]. IEEE Transactions on Vehicular Technology, 2019, 68(5): 4695–4706. doi: 10.1109/TVT.2019.2902561 JEONG J, PARK Y, WEON S, et al. Eigendecomposition-based GFDM for interference-free data transmission and pilot insertion for channel estimation[J]. IEEE Transactions on Wireless Communications, 2018, 17(10): 6931–6943. doi: 10.1109/TWC.2018.2864995 EHSANFAR S, MATTHÉ M, CHAFII M, et al. Pilot-and CP-aided channel estimation in MIMO non-orthogonal multi-carriers[J]. IEEE Transactions on Wireless Communications, 2019, 18(1): 650–664. doi: 10.1109/TWC.2018.2883940 GOLDSMITH A. Wireless Communications[M]. New York: Cambridge University Press, 2005: 71–74. KOZEK W and MOLISCH A F. Nonorthogonal pulseshapes for multicarrier communications in doubly dispersive channels[J]. IEEE Journal on Selected Areas in Communications, 1998, 16(8): 1579–1589. doi: 10.1109/49.730463 NISSEL R, ADEMAJ F, and RUPP M. Doubly-selective channel estimation in FBMC-OQAM and OFDM systems[C]. The 88th IEEE Vehicular Technology Conference, Chicago, USA, 2018: 1–5. KAY S M. Fundamentals of Statistical Signal Processing: Estimation Theory[M]. Englewood Cliffs: PTR Prentice-Hall, 1993: 344–365. -





 下载:
下载:



 下载:
下载:
