雷达与电子支援措施异步抗差航迹关联算法

衣晓; 杜金鹏

doi:10.11999/JEIT200250

雷达与电子支援措施异步抗差航迹关联算法

doi: 10.11999/JEIT200250

衣晓,
杜金鹏^,

海军航空大学烟台 264001

基金项目: 国防科技卓越青年人才基金(2017-JCJQ-ZQ-003)，泰山学者工程专项经费(ts201712072)

详细信息

作者简介:
衣晓：男，1976年生，教授，博士生导师，研究方向为无线传感器网络、多源信息融合

杜金鹏：男，1995年生，硕士生，研究方向为数据关联

通讯作者:
杜金鹏　jpdu_1409@163.com

中图分类号: TN953; V271.4
计量
- 文章访问数: 1086
- HTML全文浏览量: 513
- PDF下载量: 65
- 被引次数: 12
出版历程
- 收稿日期: 2020-04-07
- 修回日期: 2020-11-01
- 网络出版日期: 2020-12-09
- 刊出日期: 2021-07-10

Asynchronous Anti-bias Track Association Algorithm of Radar and Electronic Support Measurements

Xiao YI,
Jinpeng DU^,

Naval Aviation University, Yantai 264001, China

Funds: The Excellent Youth Scholar of the National Defense Science and Technology Foundation of China (2017-JCJQ-ZQ-003), The Special Fund for the Taishan Scholar Project (ts201712072)

摘要

摘要: 针对雷达与电子支援措施(ESM)存在系统误差、航迹异步等复杂条件下的航迹关联问题，该文提出一种基于区间序列离散度的异步抗差航迹关联算法。定义混合区间序列的离散信息度量，给出系统误差的区间化方法，通过计算区间离散度并利用经典分配法进行关联判定。与传统算法相比，可在系统误差存在的前提下无需时域配准对异步航迹直接关联，且对噪声分布不敏感。仿真结果表明，所提算法具有良好的抗差性且不受目标运动位置的影响，适用于传感器同地或异地配置等多种情况。
- 雷达 /
- 电子支援措施 /
- 航迹关联 /
- 系统误差 /
- 异步航迹 /
- 离散度
Abstract: To address track association problem of radar and Electronic Support Measurements (ESM) under complex conditions such as system biases and asynchronous track, an asynchronous anti-bias track association algorithm based on discrete degree of interval sequence is proposed. The discrete information measurement of mixed interval sequence is defined and the interval method of system biases is given. The association determination is performed by calculating the interval discrete degree and using classical assignment method. Compared with the traditional algorithm, the asynchronous track can be directly correlated without time-domain registration in the presence of system errors and it is not sensitive to noise distribution. The simulation results show that the algorithm has good robust performance and is not affected by the target moving position. The algorithm can be applied to the configuration of sensors at same or different sites.
- Radar /
- Electronic Support Measurements (ESM) /
- Track association /
- System bias /
- Asynchronous track /
- Discrete degree

HTML全文

1. 引言

现代战场环境复杂，电子战装备呈现高度集成化、综合化发展趋势，释放干扰形式多样，特别是数字射频存储器(Digital Radio Frequency Memory, DRFM)技术在雷达对抗领域中的广泛应用^[1,2]，使得干扰信号与雷达信号在多个参数域重叠，导致常用时频域抗干扰方法失效。在如此严峻的干扰环境下，目标源DOA估计方法的性能将大打折扣。此外，目标源的非合作性导致有效样本数少。所以，研究有源欺骗干扰环境下，基于小样本的DOA估计方法具有重要意义。

常规的DOA估计算法有两类，第1类是最大似然DOA估计算法，在高信噪比情况下可接近克拉美罗界，但运算量非常大。虽然存在很多优化算法应用到最大似然DOA估计中以降低运算量^[3–5]，但还是面临寻优速度慢、精度不够的问题；第2类是子空间类算法，这类算法基于空间搜索，运算量大，而且不适用于相干信号源DOA估计。虽然存在很多算法用于改善相干源下子空间类算法的DOA估计性能^[6,7]，但多数算法基于特定的阵列结构，限制了算法的实用性。近几年兴起的稀疏重构类算法为DOA估计开辟了新思路^[8–11]。相比于其他稀疏重构类算法，稀疏贝叶斯学习算法具备较大优势。首先，稀疏贝叶斯学习算法的全局最小点通常是稀疏解，而广泛使用的基于L1惩罚项的算法在限定条件下才可以满足^[12]；其次，当感知矩阵列相关性很强时，大多数稀疏重构类算法失效，但稀疏贝叶斯学习算法仍有较好性能^[13]。稀疏贝叶斯DOA估计通常将DOA估计问题转化为基于多测量矢量(Multiple Measurement Vectors, MMV)模型的稀疏重构问题，根据贝叶斯准则获取后验概率函数，利用EM(Evidence Maximization)等算法得到超参数估计，进而估计来波方向。基于块稀疏贝叶斯学习(Block Sparse Bayesian Learning, BSBL)^[13–15]的DOA估计利用Kronecker积将MMV模型转化为具有块结构的SMV(Single Measurement Vector, SMV)模型，MMV模型下的非零行对应SMV模型下的非零块，再利用稀疏贝叶斯学习得到DOA估计。因为，BSBL算法既利用了统计信息又利用了结构信息，所以DOA估计的稳健性得以提高。

以上DOA估计算法工作在无干扰环境时性能较好，但有源欺骗干扰的存在会降低算法的DOA估计性能^[16,17]。极化域作为继时域、频域、空域后的又一重要信号域，若可以充分利用雷达信号和干扰信号在该域的差异，抗干扰性能将得以提升。Nathanson^[18]早先提出自适应极化对消器，用于研究雨杂波对消问题，之后，出现实时性较好的自适应极化滤波(Adaptive Polarization Filter, APF)包括极化状态估计和最佳极化接收两部分，通过调整接收天线极化形式，使其与干扰极化形式正交，从而抑制干扰信号，提高信干比^[19,20]。

针对有源欺骗干扰环境下基于小样本的DOA估计问题，本文将APF与BSBL算法联合，实现了干扰环境下的高精度DOA估计。首先通过APF抑制干扰，提高信干比。之后，建立有源欺骗干扰环境下的稀疏贝叶斯模型，利用相邻采样时间相关性，将MMV模型转化为具有块稀疏特性的SMV模型，采用BSBL算法进行DOA估计。在仿真中，先在不同信噪比条件下，分析了所提算法的DOA估计性能与干扰和目标的极化角度差以及算法迭代次数的关系。然后，在有源欺骗干扰、小样本环境下，将所提方法与BSBL算法、APF联合子空间类算法和APF联合最大似然DOA估计算法进行对比，仿真和实测数据处理结果验证了所提方法具有较高的空间分辨率和测角精度。

2. 有源欺骗干扰环境下信号模型

正交极化双通道测量是获取入射电磁波极化信息的物理前提，到达接收天线的信号极化矢量表示为

${{h}} = [{{{h}}_{\rm{h}}}, {{{h}}_{\rm{v}}}] = \left[ {\begin{array}{*{20}{c}} {\cos(\alpha )}&{\sin(\alpha ){{\rm{e}}^{({\rm{j}}\phi )}}} \end{array}} \right]$

(1)

其中，h和v表示接收天线正交极化双通道， $\alpha$ 和 $\phi$ 决定信号的极化状态。

雷达信号的极化矢量表示为

$\begin{array}{*{20}{c}} {{{{h}}_q} = [\!\begin{array}{*{20}{c}} {\cos({\alpha _q})}&{\sin({\alpha _q}){{\rm{e}}^{(j{\phi _q})}}} \end{array}\!], }&{q = 1, 2, ·\!·\!· , Q} \end{array}$

(2)

其中， $Q$ 为目标数目。干扰信号极化矢量表示为

$\!\begin{array}{*{20}{c}} {{{h}}_k^1 = [\!\!\begin{array}{*{20}{c}} {\cos(\alpha _k^1)}&{\sin(\alpha _k^1){{\rm{e}}^{({\rm j}{\phi _k})}}} \end{array}\!\!], }&{k = 1, 2, ·\!·\!· , K} \end{array}$

(3)

其中， $K$ 为干扰数目。

弹载雷达接收信号由3部分构成：目标信号、干扰信号和噪声信号。目标信号表示为

$\!\!\!\!\begin{array}{*{20}{c}} {{{{S}}_q} \!=\! \left[\! {{{\rm{e}}^{\left[ {{\rm{j}}\frac{{2{{π}} }}{\lambda }d\sin({\theta _q}){{(0:M - 1)}^{\rm{T}}}} \right]}}\!{{{g}}_q}(t)}\! \right]\! \otimes \!{{{h}}_q}, }\;{q \!=\! 1, 2, ·\!·\!· , Q} \end{array}$

(4)

其中， ${\theta _q}$ 表示目标方位角，d为均匀线阵的阵元间距， $M$ 为阵元数。 ${{{g}}_q}(t)$ 表示第 $q$ 个目标的回波复包络， $\otimes$ 表示Kronecker积运算。雷达接收到的干扰信号表示为

$\!\!\!\!\!\!\begin{array}{*{20}{c}} {{{{J}}_k} \!=\! \left[\! {{{\rm{e}}^{\left[ {{\rm{j}}\frac{{2{{π}} }}{\lambda }d\sin(\theta _k^1){{(0:M - 1)}^{\rm{T}}}} \right]}}{{{j}}_k}(t)}\! \right]\! \otimes \!{{h}}_k^1, }\;{k \!=\! 1, 2, ·\!·\!· , K} \end{array}$

(5)

其中， $\theta _k^1$ 表示干扰方位角， ${{{j}}_k}(t)$ 表示第 $k$ 个干扰信号的复包络。天线接收到的总信号 ${{X}}$ 表示为

${{X}} = \sum\limits_{{{q = 1}}}^Q {{{{S}}_q}} + \sum\limits_{{{k = 1}}}^K {{{{J}}_k}} +{{{N}}\!_{s}}$

(6)

其中， ${{{N}}\!_{s}}$ 表示互不相关的加性高斯白噪声。

3. APF联合BSBL算法的DOA估计方法

弹载雷达接收信号 ${{X}}$ 中包含多个有源欺骗干扰信号，在有限信噪比和迭代次数下，影响的BSBL算法DOA估计性能。将APF联合BSBL算法可提高BSBL算法在有源欺骗干扰环境下DOA估计性能。

APF抑制干扰的前提是知道干扰信号的极化信息。记接收电场的极化相干矩阵为 ${{C}}$ ，表示如式(7)

${{C}} = \left[ {\begin{array}{*{20}{c}} {{C_{{\rm{hh}}}}}&{{C_{{\rm{hv}}}}} \\ {{C_{{\rm{vh}}}}}&{{C_{{\rm{vv}}}}} \end{array}} \right]$

(7)

极化信息可完全由 ${{C}}$ 决定，实际应用中不可先验得到，它的最大似然估计为

$\hat {{C}} = \frac{1}{N}\sum\limits_{n = 1}^N {{{X}}_n^{\rm{H}}{{{X}}_n}}$

(8)

其中， $N$ 为回波样本数， ${{{X}}_n} = \left[ {{{{X}}_{n{\rm{h}}}}, {{{X}}_{n{\rm{v}}}}} \right]$ ， ${{{X}}_{n{\rm{h}}}}$ 和 ${{{X}}_{n{\rm{v}}}}$ 分别表示 ${{{X}}_{\rm{h}}}$ 和 ${{{X}}_{\rm{v}}}$ 的第 $n$ 列。假设 $n$ 时刻极化相干矩阵估计为 ${\hat{{C}}_n}$ , $n + 1$ 时刻的极化相干矩阵估计 ${\hat {{C}}_{n + 1}}$ 通过迭代得到，具体步骤如下：

(1)初始值 ${\hat {{C}}_0} = \left[ {\begin{array}{*{20}{c}} 1&{\rm{j}} \\ { - {\rm{j}}}&1 \end{array}} \right]$ 。

(2) ${\hat {{C}}_{n + 1}}$ 的迭代公式如式(9)

${\hat {{C}}_{n + 1}} = (1 - \zeta ){\hat {{C}}_n} + \zeta {{X}}_{n + 1}^{\rm{H}}{{{X}}_{n + 1}}$

(9)

其中， $n = 0, 1, \cdots , { N} - 1$ 。 $0 \le \zeta \le 1$ 为新数据权重因子，反映新数据对相干矩阵估计的重要性。接收回波样本数据量越大，每个新样本对 ${\hat {{C}}_{n + 1}}$ 的作用越小。所以，可以认为与样本数 $N$ 具有反比关系，取为 ${1 / N}$ 。

极化相干矩阵 $\hat {{C}}$ 迭代完成后，对其进行特征分解，小特征值对应的特征矢量记为 ${{{u}}_{{2}}}$ 。天线最佳接收极化矢量表示为

${{{h}}_{{\rm{opt}}}} = \frac{{{{{u}}_{{2}}}^{\rm{T}}}}{{\left\| {{{{u}}_{{2}}}} \right\|}}$

(10)

获得天线最佳接收极化矢量 ${{{h}}_{{\rm{opt}}}}$ 后，对雷达接收信号 ${{X}}$ 进行干扰滤除得 ${{{X}}^{\rm{A}}}$

$\begin{array}{*{20}{c}} {{{X}}_i^{\rm{A}} = {{{X}}_i}{{h}}_{{\rm{opt}}}^{\rm{T}}, }&{i = 1, 2, ·\!·\!· , N} \end{array}$

(11)

其中， ${{X}}_i^{\rm{A}}$ 表示 ${{{X}}^{\rm{A}}}$ 的第 $i$ 列。

利用APF提高信干比得到 ${{{X}}^{\rm{A}}}$ 后，通过BSBL算法进行DOA估计。BSBL算法的数学模型是将MMV模型转化为具有块稀疏特性的SMV模型。 ${{{X}}^{\rm{A}}}$ 在基于MMV的稀疏贝叶斯模型中表示为

${{{X}}^{\rm{A}}} = {{fs}} + {{V}}$

(12)

其中， ${{f}}$ 是 $M \times L$ 的学习字典， $L$ 是空间划分格数。 ${{s}}$ 是 $L \times N$ 维的待恢复稀疏矩阵，为了得到唯一的全局最优解，应保证 ${{s}}$ 是行稀疏的。 ${{V}}$ 是 $M \times N$ 维的噪声矢量。无角度欺骗干扰时， ${{s}}$ 的元素满足

${{s}}\left( {l, :} \right) = \left\{ {\begin{array}{*{20}{l}} {{{{z}}_q}, } & {{\theta _l} = {\theta _q}}\\ {0, } & {{其它}} \end{array}} \right. , {l = 1, 2, ·\!·\!· , L}$

(13)

其中， ${{{z}}_q}$ 表示目标源信号。有角度欺骗干扰时， ${{s}}$ 的元素满足

${{s}}\left( {l, :} \right) = \left\{ {\begin{array}{*{20}{l}} {{{{z}}_q}, } & {{\theta _l} = {\theta _q}} \\ {{{{z}}_k}, } & {{\theta _l} = \theta _k^1} \\ {0, } & {{其它}} \end{array}} \right., {l = 1, 2, ·\!·\!· , L}$

(14)

其中， ${{{z}}_k}$ 表示干扰转发信号。

令

${{y}} = {\rm{vec}}({({{{X}}^{\rm{A}}})^{\rm{T}}})$

(15)

${{D}} = {{f}} \otimes {{{I}}_N} \hspace{20pt}$

(16)

${{x}} = {\rm{vec}}({{{s}}^{\rm{T}}}) \hspace{20pt}$

(17)

${{v}} = {\rm{vec}}({{{V}}^{\rm{T}}}) \hspace{18pt}$

(18)

其中， ${\rm{vec}}( \bullet )$ 代表矩阵矢量化， ${{{I}}_N}$ 表示 $N$ 维单位阵。

利用式(15)到式(18)，MMV模型转化为SMV模型，表示为

${{y}} = {{Dx}} + {{v}}$

(19)

式(19)的等价表示为

$\begin{aligned} {{y}} =& \left[ {\begin{aligned} {{{{f}}_1} \otimes {{{I}}_N}}\;\; {{{{f}}_2} \otimes {{{I}}_N}}\;\;·\!·· &{{{{f}}_L} \otimes {{{I}}_N}} \end{aligned}}\right]\\ &\cdot{\left[ {\begin{aligned} {{{x}}_1^{\rm{T}}}\;\; {{{x}}_2^{\rm{T}}}\;\;·\!·\!· \;\;{{{x}}_L^{\rm{T}}} \end{aligned}} \right]^{\rm{T}}} + {{v}} \end{aligned}$

(20)

其中， ${{x}}_i^{\rm{T} }$ 表示 ${{s}}$ 的第 $i$ 行， ${{{f}}_i}$ 表示 ${{f}}$ 的第 $i$ 列， $i = 1, 2, ·\!·\!· , L$ 。由展开式可以看出， ${{x}}$ 由 $L$ 个块组成，每个块中包含 $N$ 个元素，由于接收信号采样频率较高， $N$ 个元素间通常具有时间相关性。假设噪声矢量中元素独立且同服从参数为 $\partial$ 的高斯分布， ${{y}}$ 的似然函数为

$p({{y}}|{{x}};\partial )\sim {{\rm{N}}_{{{y}}|{{x}}}}({{Dx}}, \partial {{I}})$

(21)

似然函数的概率密度函数形式确定后，未知参数为期望和方差，需要用样本对参数进行估计。

假定待恢复稀疏矩阵 ${{s}}$ 中的每行之间独立，且服从正态分布

$\begin{array}{*{20}{c}} {p({{{s}}_i};{\gamma _i}, {{{B}}_i})\sim{\rm{N}}({{0}}, {\gamma _i}{{{B}}_i}), }&{i = 1, 2, ·\!·\!· , L} \end{array}$

(22)

其中， ${\gamma _i}$ 控制 ${{s}}$ 的行稀疏性， ${{{B}}_i}$ 为正定矩阵，用于描述 ${{{s}}_i}$ 的相关结构。

则 ${{x}}$ 的先验概率满足

$p({{x}};{\gamma _i}, {{{B}}_i}, \forall i)\sim{{\rm{N}}_{{x}}}({{0}}, {{{Σ}} _0})$

(23)

其中， ${{{Σ}} _0}$ 表示为

${{{Σ}} _0} = \left[ {\begin{array}{*{20}{c}} {{\gamma _1}{{{B}}_1}}&{}&{}&{} \\ {}&{{\gamma _2}{{{B}}_2}}&{}&{} \\ {}&{}& \ddots &{} \\ {}&{}&{}&{{\gamma _L}{{{B}}_L}} \end{array}} \right]$

(24)

为了防止过拟合， $L$ 个块采用同一个 ${{B}}$ 描述相关结构^[13]，得

${{{Σ}} _0} = {{Γ}} \otimes {{B}}$

(25)

其中， ${{Γ}} = {\rm{diag}}({\gamma _1}, {\gamma _2}, ·\!·\!· , {\gamma _L})$ ，根据贝叶斯公式，后验概率 $p({{x}}|{{y}})$ 由先验概率和似然函数表示为

$p({{x}}|{{y}}) = \frac{{p({{y}}|{{x}}){{p}}({{x}})}}{{p({{y}})}}$

利用贝叶斯准则得后验概率分布

$p({{x}}|{{y}};\partial , {\gamma _i}, {{B}}, \forall i)\sim{{\rm{N}}_{{{x}}|{{y}}}}({{{μ}} _{{x}}}, {{{Σ}} _{{x}}})$

(26)

其中，

$\begin{aligned} {{{Σ}} _{{x}}} =& {\left( {{{Σ}} _0^{ - 1} + \frac{1}{\partial }{{{D}}^{\rm{T}}}{{D}}} \right)^{ - 1}}\\ =& {{{Σ}} _0} - {{{Σ}} _0}{{{D}}^{\rm{T}}}{\left( {\partial {{I}} + {{D}}{{{Σ}} _0}{{{D}}^{\rm{T}}}} \right)^{ - 1}}{{D}}{{{Σ}} _0} \end{aligned}$

(27)

$$ {{{μ}} _{{x}}} = \frac{1}{\partial }{{{Σ}} _{{x}}}{{{D}}^{\rm{T}}}{{y}} \hspace{115pt}$

(28)

${{x}}$ 的MAP(Maximum-A-Posterior)估计为

$\begin{aligned} {{{x}}^*} \triangleq {{{μ}} _x} =& {\left( {\partial {{{Σ}} _0}^{ - 1} + {{{D}}^{\rm{T}}}{{D}}} \right)^{ - 1}}{{{D}}^{\rm{T}}}{{y}} \\ =& {{{Σ}} _0}{{{D}}^{\rm{T}}}{\left( {\partial {{I}} + {{D}}{{{Σ}} _0}{{{D}}^{\rm{T}}}} \right)^{ - 1}}{{y}} \end{aligned}$

(29)

由此可知，对参数集 ${{Θ}} = \left\{ {{\gamma _1}, {\gamma _2}, ·\!·\!· , {\gamma _L}, {{B}}, \partial } \right\}$ 进行估计，即求得稀疏解。

最大化 $p({{y}};{{Θ}} )$ 可得参数估计，相当于最小化 $- \lg p({{y}};{{Θ}} )$ ，目标函数为

$L\left( {{Θ}} \right) = {{{y}}^{\rm{T}}}{{Σ}} _{{y}}^{ - 1}{{y}} + \lg \left| {{{{Σ}} _{{y}}}} \right|$

(30)

通过最大期望(Expectation-Maximization, EM)算法，得到参数更新^[13]

$\!\!\!\begin{array}{*{20}{c}} {{\gamma _i}\! =\! \frac{{{{\rm{t}}{\rm{r}}}\left[ {{{{B}}^{ - 1}}({{Σ}} _x^i \!+\! {{μ}} _x^i{{({{μ}} _x^i)}^{\rm{T}}})} \right]}}{N}, }&{i \!=\! 1, 2, ·\!·\!· , L} \end{array}$

(31)

其中， ${{\rm{tr}}}\left[ \bullet \right]$ 表示矩阵求迹， ${{{μ}} _x^i}{\underline{\underline \Delta } } {{{μ}} _x}\left(\! {\left( {i \!-\! 1} \right)\!N \!+\! 1\!:iN} \right)$ , ${{{Σ}} _x^i}{\underline{\underline \Delta } } {{{Σ}} _x}\left( {\left( {i - 1} \right)N + 1:iN, \left( {i - 1} \right)N + 1:iN} \right)$ 。

${{B}} = \frac{1}{L}\sum\limits_{i = 1}^L {\frac{{{{Σ}} _x^i + {{μ}} _x^i{{({{μ}} _x^i)}^{\rm{T}}}}}{{{\gamma _i}}}}$

(32)

为了增加鲁棒性，按以下规则对 ${{B}}$ 进行估计

${{B}} = {{\mathop {{B}}\limits^ \approx } /{||\mathop {{B}}\limits^ \approx |{|_{\rm{F}}}}}$

(33)

其中， $\mathop {{B}}\limits^ \approx = \displaystyle\sum\nolimits_{i = 1}^L {\frac{{{{μ}} _x^i{{({{μ}} _x^i)}^{\rm{T}}}}}{{{\gamma _i}}}} + h{{I}}$ , $h$ 为一正的常量， $||\mathop {{B}}\limits^ \approx |{|_{\rm{F}}}$ 表示 $\mathop {{B}}\limits^ \approx$ 的Frobenius范数。 $\partial$ 的迭代公式为

$\partial = \frac{{\left\| {{{y}} - {{D}}{{{μ}} _x}} \right\|_2^2 + \partial \left[ {LN - {{\rm{tr}}}({{{Σ}} _x}{{Σ}} _0^{ - 1})} \right]}}{{MN}}$

(34)

当达到设定的迭代次数小于门限时，停止迭代，此时， ${{\gamma _i}, }i = 1, 2, ·\!·\!· , L$ 中最大值对应目标方位。

4. 仿真与实测分析

4.1 仿真实验

仿真条件：仿真采用正交极化双通道阵列天线接收信号，基于7阵元均匀线阵，阵元间距取波长的一半。载波波段为C波段，信号形式为线性调频信号，带宽为4 MHz，采样频率为5 MHz。

(1)为验证干扰信号和雷达信号的极化角度差以及迭代次数对本文方法测角性能的影响，下面对本文方法测角误差进行仿真分析。目标雷达数目为1，方位角为10°，极化矢量固定为 ${{{h}}_1} \!=\!\! \left[\!\!\!\! {\begin{array}{*{20}{c}} {\cos(45^\circ)}\;{\sin(45^\circ){{\rm{e}}^{({\rm{j}}0^\circ)}}} \end{array}} \!\!\!\!\right]$ 。干扰数目为1，方位角为–10°，极化矢量为 ${{h}}_1^1 =$ $\left[\!\!\!\! {\begin{array}{*{20}{c}} {\cos(45^\circ)}\;{\sin(45^\circ){{\rm{e}}^{({\rm{j}}\Delta \phi )}}} \end{array}} \!\!\!\!\right]$ ，其中， $\Delta \phi$ 的变化间隔为0.5°，变化范围为[12.0° 24.5°]。接收信号前面采样数据信干比为–3 dB，用于干扰极化状态估计，后面采样数据信干比为0 dB。固定BSBL算法迭代次数为100次，本文方法的测角误差随目标和干扰的极化角度差变化曲线如图1(a)所示。然后，固定干扰极化矢量 ${{h}}_1^1 = \left[\!\!\!\! {\begin{array}{*{20}{c}} {\cos(45^\circ)}\;{\sin(45^\circ){{\rm{e}}^{({\rm{j}}40^\circ)}}} \end{array}} \!\!\!\!\right]$ ，迭代次数的变化间隔为2次，变化范围为[108次 160次]，本文方法的测角误差随迭代次数变化的曲线如图1(b)所示。

图 1 APF联合BSBL算法的测角性能分析

下载: 全尺寸图片幻灯片

由图1(a)可知，信噪比越高，测角误差越小，同一信噪比下，目标和干扰极化角度差越大，测角误差越小，并逐步趋于稳定；由图1(b)可知，信噪比越高，对迭代次数的要求越小，同一信噪比下，迭代次数越大，测角误差越小，并逐步趋于稳定。

(2)为验证有源欺骗干扰环境和小样本条件下所提方法DOA估计的性能，将本文方法与BSBL算法、APF联合子空间类算法、APF联合最大似然(Maximum Likelihood, ML)算法进行对比。信噪比取为20 dB，样本数为5，干扰数目为1，方位为10°，目标数目为2，方位分别为18°和25°。干扰极化矢量为 ${{h}}_1^1 = \left[\!\!\!\! {\begin{array}{*{20}{c}} {\cos(45^\circ)}\;{\sin(45^\circ){{\rm{e}}^{({\rm{j}}90^\circ)}}} \end{array}} \!\!\!\!\right]$ ，目标1极化矢量为 ${{{h}}_1} = \left[\!\!\!\! {\begin{array}{*{20}{c}} {\cos(45^\circ)}\;{\sin(45^\circ){{\rm{e}}^{({\rm{j}}0^\circ)}}} \end{array}} \!\!\!\!\right]$ ，目标2极化矢量为 ${{{h}}_2} = \left[\!\!\!\! {\begin{array}{*{20}{c}} {\cos(45^\circ)}\;{\sin(45^\circ){{\rm{e}}^{({\rm{j}}20^\circ)}}} \end{array}} \!\!\!\!\right]$ 。不同方法DOA估计结果如图2所示。

图 2 样本数为5时DOA估计结果图

下载: 全尺寸图片幻灯片

由图2可知，BSBL算法的估计结果偏离正确的方位角，干扰信号影响BSBL算法的稀疏恢复性能，这是因为待测源个数增多要求信噪比和BSBL算法迭代次数增加，导致BSBL算法测角性能下降；通过APF联合子空间类算法进行DOA估计，由于阵元数目较少、样本数少，子空间类算法空间分辨率有限，不可以同时对两个目标源进行准确的DOA估计；APF联合最大似然算法也分辨率不足，无法对两个目标进行准确的DOA估计；本文方法先通过APF滤除干扰，再通过BSBL进行DOA估计，可以分辨两个目标源，测得两个目标源方位角分别为18°和26°。综上所述，在有源欺骗干扰环境、阵元数少和小样本条件下，本文方法具有较高的空间分辨率和测角精度。

4.2 实测实验

实测场景和条件：实验采用基于弹载的正交极化双通道阵列天线接收信号，基于7阵元非均匀圆阵。为有效掩护雷达信号，干扰辐射功率高于雷达平均副瓣1～3 dB，并低于雷达主瓣约20～25 dB。各干扰源的辐射强度基本相同，天线指向固定，因此，弹载雷达收到的干扰信号功率相对稳定。典型配置为3个干扰，为了更好的干扰弹载雷达系统，使其不能准确测量雷达信号源方向，一般沿雷达两侧及径向布置有源欺骗干扰，布设距离100～300 m。雷达主瓣极化形式多为线极化，而雷达副瓣的极化形式较为杂乱，但此时雷达功率低于干扰功率较多。干扰场景如图3所示。

图 3 干扰场景图

下载: 全尺寸图片幻灯片

为在时-频-空域保护目标，干扰信号脉冲覆盖雷达信号脉冲的前后沿。干扰信号与雷达信号的载频、重频等参数相同或接近，3个干扰分布在雷达主瓣内，时-频-空域抑制干扰手段失效。导弹对雷达进行初始探测时，接收到的信号来自雷达副瓣和干扰。所以，初始探测采样数据可以近似为干扰数据，用于极化状态估计，进而在极化域实现抗干扰。在导弹攻击过程中，初始阶段干扰与弹载雷达的空间角度差较小，随着弹目不断接近，空间角度差逐渐变大。参考方向如图4所示。

图 4 干扰和弹载雷达方位角和仰角分布图

下载: 全尺寸图片幻灯片

因为仰角和方位角的2维测量导致冗余字典长度增加，所以利用本文方法进行DOA估计时，先进行大范围粗略估计，再进行小范围精确估计。仿真实验中用到的ESPRIT算法利用自相关矩阵信号子空间旋转不变性，从子阵固定关系中求得来波方向，在测角前需要先将总阵分为几个布局一致的子阵。由此可知，ESPRIT算法不适用于基于非均匀圆阵的DOA估计。所以实测数据处理时仅将所提方法与APF联合MUSIC算法和APF联合ML算法进行对比。为了定量评估DOA估计精度，测角误差表示为方位和仰角测角误差的均方根。基于接收到的20个脉冲信号，3种方法的测角均方根误差如图5所示。

图 5 实测数据测角均方根误差图

下载: 全尺寸图片幻灯片

由图5可知，本文方法同样适用于干扰环境下基于非均匀圆阵的2维DOA估计。在有源欺骗干扰和小样本环境下，相比APF联合MUSIC算法或最大似然算法，本文方法具有更高的测角精度。

5. 结束语

有源欺骗干扰的存在使得待测源个数增多，影响BSBL算法测向性能。因此，本文提出APF联合BSBL算法，用于有源欺骗干扰环境下基于小样本的DOA估计。本文方法先基于接收数据估计干扰极化状态，进而在极化域抑制干扰信号。然后，通过BSBL算法估计目标方向，有效提高了有源欺骗干扰环境下BSBL算法的测向性能。仿真和实测实验处理结果表明本文方法在有源欺骗干扰环境下具有较高的测角精度和空间分辨率。如何进一步降低本文方法运算量，使其可以应用于更为复杂的战场环境，将是今后的研究重点。

图 1 系统误差示意图

下载: 全尺寸图片幻灯片

图 2 算法流程图

下载: 全尺寸图片幻灯片

图 3 方位角量测误差下的正确关联率对比

下载: 全尺寸图片幻灯片

图 4 不同采样率之比下的正确关联率对比

下载: 全尺寸图片幻灯片

图 5 不同目标数目时的正确关联率对比

下载: 全尺寸图片幻灯片

图 6 正确关联率随目标运动位置的变化

下载: 全尺寸图片幻灯片

表 1 雷达与ESM最大系统误差取值表

实验编号	1	2	3	4	5	6
$\Delta \theta _{\rm{m}}^s(^\circ )$	0.5	0.5	1.0	1.5	0.5	0.5
$\Delta \theta _{\rm{m}}^w(^\circ )$	0.5	0.5	0.5	0.5	1.0	1.5
$\Delta \rho _{\rm{m}}^s({\rm{m)}}$	500	1000	500	500	500	500

下载: 导出CSV

表 2 不同系统误差下的算法关联率对比

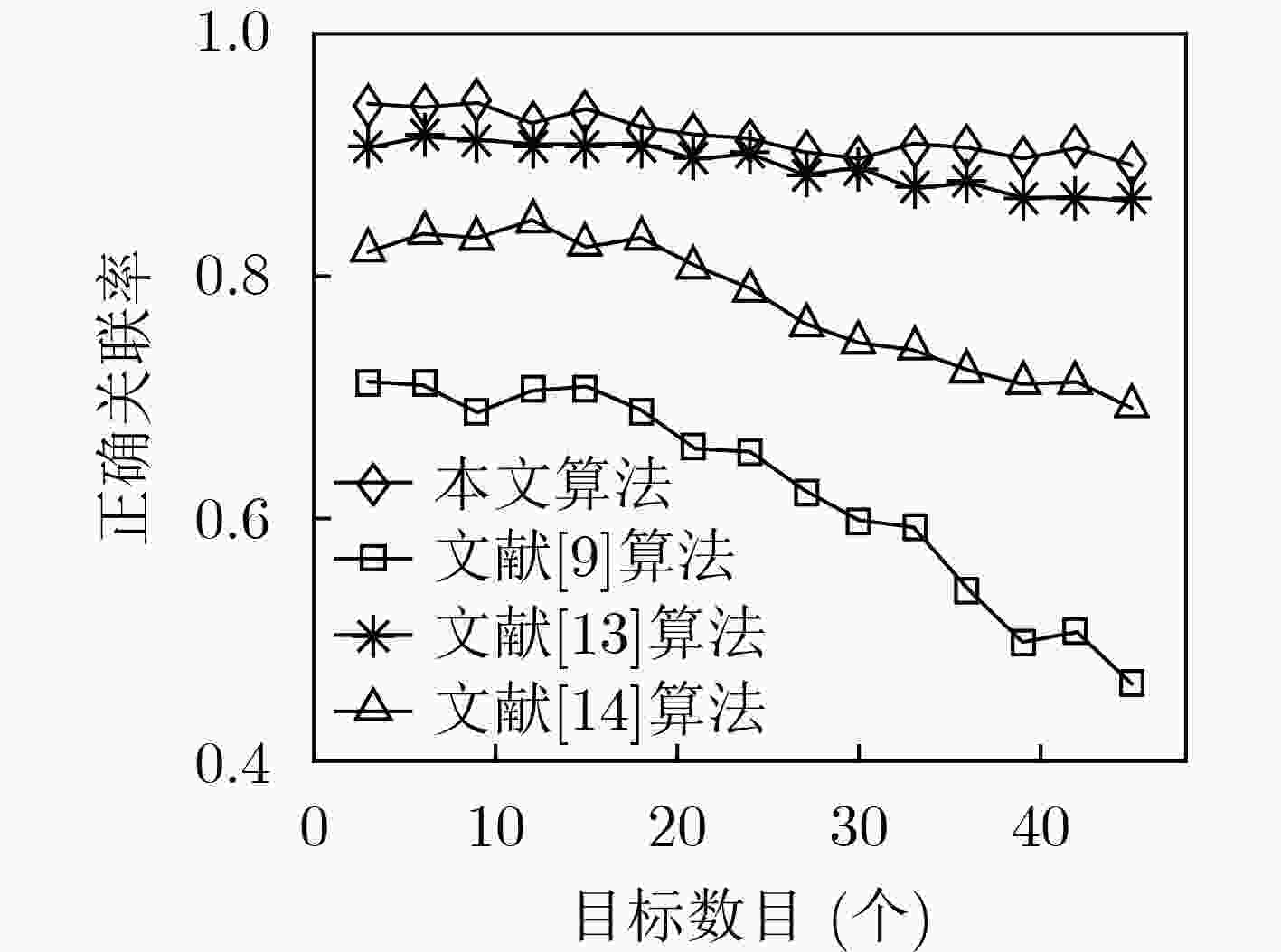
实验编号	本文算法			文献[9]算法			文献[13]算法			文献[14]算法
实验编号	E_c	E_e	E_s	E_c	E_e	E_s	E_c	E_e	E_s	E_c	E_e	E_s
1	0.937	0.056	0.007	0.743	0.075	0.182	0.936	0.028	0.036	0.866	0.023	0.111
2	0.932	0.060	0.008	0.698	0.049	0.253	0.935	0.033	0.032	0.858	0.024	0.118
3	0.914	0.054	0.032	0.504	0.175	0.321	0.900	0.044	0.056	0.817	0.078	0.105
4	0.892	0.056	0.052	0.445	0.243	0.312	0.881	0.058	0.061	0.772	0.026	0.202
5	0.944	0.047	0.009	0.506	0.090	0.404	0.937	0.023	0.040	0.840	0.048	0.112
6	0.933	0.056	0.011	0.456	0.234	0.310	0.925	0.038	0.037	0.787	0.051	0.162

下载: 导出CSV

表 3 不同目标运动模型下的正确关联率

目标运动模型	匀速直线运动	匀加速直线运动	变加速直线运动	匀速圆周运动
正确关联率	0.931	0.928	0.923	0.917

下载: 导出CSV

表 4 不同采样周期和开机时延的正确关联率

ESM开机时延(s)	雷达，ESM采样周期(时间间隔)(s)
ESM开机时延(s)	t₁=0.1,t₂=0.3	t₁=0.3,t₂=0.5	t₁=0.5,t₂=1.1
Δt=0.1	0.913	0.913	0.834
Δt=0.2	0.922	0.891	0.844
Δt=0.3	0.928	0.890	0.820
Δt=0.4	0.927	0.881	0.831

下载: 导出CSV

表 5 不同噪声分布的正确关联率

噪声分布形式	高斯分布	瑞利分布	指数分布	均匀分布
正确关联率	0.926	0.920	0.914	0.934

下载: 导出CSV

参考文献(18)

[1]	何友, 王国宏, 关欣, 等. 信息融合理论及应用[M]. 北京: 电子工业出版社, 2010: 124–146. HE You, WANG Guohong, GUAN Xin, et al. Information Fusion Theory with Applications[M]. Beijing: Publishing House of Electronics Industry, 2010: 124–146.
[2]	TU Yongiun, HUANG Gaoming, LI Jinghui, et al. Performance analysis of radar and ESM track association algorithms[J]. Applied Mechanics and Materials, 2011, 130–134: 1925–1928. doi: 10.4028/www.scientific.net/AMM.130-134.1925
[3]	WANG Guohong, MAO Shiyi, and HE You. Analytical performance evaluation of association of active and passive tracks for airborne sensors[J]. Signal Processing, 2003, 83(5): 973–981. doi: 10.1016/s0165-1684(02)00500-5
[4]	OFFER C R. Performance of bearing-only ESM-radar track association[C]. Proceedings of the 9th IET Data Fusion & Target Tracking Conference, London, UK, 2012: 1–6. doi: 10.1049/cp.2012.0409.
[5]	WANG Guohong, MAO Shiyi, HE You, et al. Triple-threshold radar-to-ESM correlation algorithm when each radar track is specified by different number of measurements[J]. IEE Proceedings - Radar, Sonar and Navigation, 2000, 147(4): 177–181. doi: 10.1049/ip-rsn:20000094
[6]	WANG Guohong, HE You, MAO Shiyi, et al. Quadri-threshold algorithm of co-located radar-to-ESM correlation[J]. Chinese Journal of Aeronautics, 2000, 13(2): 86–90.
[7]	陈中华, 王国宏, 刘德浩, 等. 基于几何法的雷达与ESM航迹关联算法[J]. 电光与控制, 2012, 19(4): 10–12, 22. doi: 10.3969/j.issn.1671-637X.2012.04.003 CHEN Zhonghua, WANG Guohong, LIU Dehao, et al. Radar-ESM track correlation based on geometric method[J]. Electronics Optics &Control, 2012, 19(4): 10–12, 22. doi: 10.3969/j.issn.1671-637X.2012.04.003
[8]	关欣, 彭彬彬, 衣晓. 基于区间重合度的雷达与ESM航迹关联算法[J]. 雷达科学与技术, 2017, 15(1): 61–67. doi: 10.3969/j.issn.1672-2337.2017.01.011 GUAN Xin, PENG Binbin, and YI Xiao. Track association algorithm of radar and ESM based on the interval overlap ratio[J]. Radar Science and Technology, 2017, 15(1): 61–67. doi: 10.3969/j.issn.1672-2337.2017.01.011
[9]	宋振宇, 张翔宇, 张光轶. 系统误差对异地配置的雷达和ESM航迹关联的影响[J]. 电光与控制, 2014, 21(3): 42–46. doi: 10.3969/j.issn.1671-637X.2014.03.010 SONG Zhenyu, ZHANG Xiangyu, and ZHANG Guangyi. Effect of systematic errors on radar-to-ESM track association at different sites[J]. Electronics Optics &Control, 2014, 21(3): 42–46. doi: 10.3969/j.issn.1671-637X.2014.03.010
[10]	张翔宇, 王国宏, 王娜, 等. 系统误差下异地配置的雷达和电子支援测量航迹关联[J]. 电光与控制, 2012, 19(3): 30–35, 43. doi: 10.3969/j.issn.1671-637X.2012.03.007 ZHANG Xiangyu, WANG Guohong, WANG Na, et al. Track association of radar and ESM sensors with systematic errors at different sites[J]. Electronics Optics &Control, 2012, 19(3): 30–35, 43. doi: 10.3969/j.issn.1671-637X.2012.03.007
[11]	ZHANG Feihu and KNOLL A. Systematic error modeling and bias estimation[J]. Sensors, 2016, 16(5): 729. doi: 10.3390/s16050729
[12]	WANG Guohong, ZHANG Xiangyu, and TAN Shuncheng. Effect of biased estimation on radar-to-ESM track association[J]. Journal of Systems Engineering and Electronics, 2012, 23(2): 188–194. doi: 10.1109/JSEE.2012.00024
[13]	李保珠, 张林, 董云龙, 等. 基于航迹矢量分级聚类的雷达与电子支援措施抗差关联算法[J]. 电子与信息学报, 2019, 41(6): 1310–1316. doi: 10.11999/JEIT180714 LI Baozhu, ZHANG Lin, DONG Yunlong, et al. Anti-bias track association algorithm of radar and electronic support measurements based on track vectors hierarchical clustering[J]. Journal of Electronics &Information Technology, 2019, 41(6): 1310–1316. doi: 10.11999/JEIT180714
[14]	关欣, 彭彬彬, 衣晓. 修正极坐标系下雷达与ESM航迹对准关联[J]. 航空学报, 2017, 38(5): 320668. doi: 10.7527/S1000-6893.2016.0287 GUAN Xin, PENG Binbin, and YI Xiao. Track alignment-association of radar and ESM in MPC[J]. Acta Aeronautica et Astronautica Sinica, 2017, 38(5): 320668. doi: 10.7527/S1000-6893.2016.0287
[15]	李保珠, 关键, 董云龙. 基于航迹矢量检测的雷达与电子支援设施抗差关联算法[J]. 电子与信息学报, 2019, 41(1): 123–129. doi: 10.11999/JEIT180303 LI Baozhu, GUAN Jian, and DONG Yunlong. Anti-bias track association algorithm of radar and electronic support measurements based on track vectors detection[J]. Journal of Electronics &Information Technology, 2019, 41(1): 123–129. doi: 10.11999/JEIT180303
[16]	ZHU Hongyan and WANG Chen. Joint track-to-track association and sensor registration at the track level[J]. Digital Signal Processing, 2015, 41: 48–59. doi: 10.1016/j.dsp.2015.03.012
[17]	左燕, 陈志猛, 蔡立平. 基于约束总体最小二乘的单站DOA/TDOA联合误差校正与定位算法[J]. 电子与信息学报, 2019, 41(6): 1317–1323. doi: 10.11999/JEIT180655 ZUO Yan, CHEN Zhimeng, and CAI Liping. Single-observer DOA/TDOA Registration and passive localization based on constrained total least squares[J]. Journal of Electronics &Information Technology, 2019, 41(6): 1317–1323. doi: 10.11999/JEIT180655
[18]	衣晓, 杜金鹏. 基于分段序列离散度的异步航迹关联算法[J]. 航空学报, 2020, 41(7): 323694. doi: 10.7527/S1000-6893.2020.23694 YI Xiao and DU Jinpeng. Asynchronous track-to-track association algorithm based on discrete degree of segmented sequence[J]. Acta Aeronautica et Astronautica Sinica, 2020, 41(7): 323694. doi: 10.7527/S1000-6893.2020.23694

施引文献

期刊类型引用(7)

1.	赵书红，董绍武，白杉杉，高喆. 一种优化的频率驾驭算法研究. 电子与信息学报. 2021(05): 1457-1464 . 本站查看
2.	陶贵丽，刘文强，张兴华，牛晓霞. 带丢包不确定广义系统鲁棒Kalman预报器. 系统科学与数学. 2021(05): 1215-1232 . 百度学术
3.	谢卫，王前东. 一种基于自适应网格剖分的协方差交集融合新算法. 电讯技术. 2019(09): 1067-1074 . 百度学术
4.	刘振亚，高敏，程呈. 基于理想弹道鲁棒容积卡尔曼滤波视线角估计. 系统工程与电子技术. 2018(02): 409-416 . 百度学术
5.	秦文利，胡捍英，陈松. 基于带势概率假设密度粒子滤波的MIMO雷达检测前跟踪算法. 信息工程大学学报. 2018(02): 140-145 . 百度学术
6.	王雪梅，刘文强，邓自立. 带丢失观测和不确定噪声方差系统改进的鲁棒协方差交叉融合稳态Kalman滤波器. 控制理论与应用. 2016(07): 973-979 . 百度学术
7.	王雪梅，刘文强，邓自立. 带不确定协方差线性相关白噪声系统改进的鲁棒协方差交叉融合稳态Kalman估值器. 控制与决策. 2016(10): 1749-1756 . 百度学术

其他类型引用(5)

资源附件(0)

访问统计

图(6) / 表(5)

计量

文章访问数: 1086
HTML全文浏览量: 513
PDF下载量: 65
被引次数: 12

1. 引言
2. 有源欺骗干扰环境下信号模型
3. APF联合BSBL算法的DOA估计方法
4. 仿真与实测分析
4.1 仿真实验
4.2 实测实验
5. 结束语

姓名
邮箱
手机号码
标题
留言内容
验证码

留言板

雷达与电子支援措施异步抗差航迹关联算法

doi: 10.11999/JEIT200250

作者简介:
衣晓：男，1976年生，教授，博士生导师，研究方向为无线传感器网络、多源信息融合

杜金鹏：男，1995年生，硕士生，研究方向为数据关联

通讯作者:
杜金鹏　jpdu_1409@163.com

计量

Asynchronous Anti-bias Track Association Algorithm of Radar and Electronic Support Measurements

1. 引言

2. 有源欺骗干扰环境下信号模型

3. APF联合BSBL算法的DOA估计方法

4. 仿真与实测分析

4.1 仿真实验

4.2 实测实验

5. 结束语

期刊类型引用(7)

其他类型引用(5)

计量

目录

1. 引言

2. 有源欺骗干扰环境下信号模型

3. APF联合BSBL算法的DOA估计方法

4. 仿真与实测分析

4.1 仿真实验

4.2 实测实验

5. 结束语

留言板

雷达与电子支援措施异步抗差航迹关联算法

doi: 10.11999/JEIT200250

作者简介: 衣晓：男，1976年生，教授，博士生导师，研究方向为无线传感器网络、多源信息融合 杜金鹏：男，1995年生，硕士生，研究方向为数据关联

通讯作者: 杜金鹏 jpdu_1409@163.com

计量

出版历程

Asynchronous Anti-bias Track Association Algorithm of Radar and Electronic Support Measurements

1. 引言

2. 有源欺骗干扰环境下信号模型

3. APF联合BSBL算法的DOA估计方法

4. 仿真与实测分析

4.1 仿真实验

4.2 实测实验

5. 结束语

期刊类型引用(7)

其他类型引用(5)

计量

出版历程

目录

1. 引言

2. 有源欺骗干扰环境下信号模型

3. APF联合BSBL算法的DOA估计方法

4. 仿真与实测分析

4.1 仿真实验

4.2 实测实验

5. 结束语

作者简介:
衣晓：男，1976年生，教授，博士生导师，研究方向为无线传感器网络、多源信息融合

杜金鹏：男，1995年生，硕士生，研究方向为数据关联

通讯作者:
杜金鹏　jpdu_1409@163.com