Research on Virtual Channel Hybrid Scheduling Algorithm in Advanced Orbit System
-
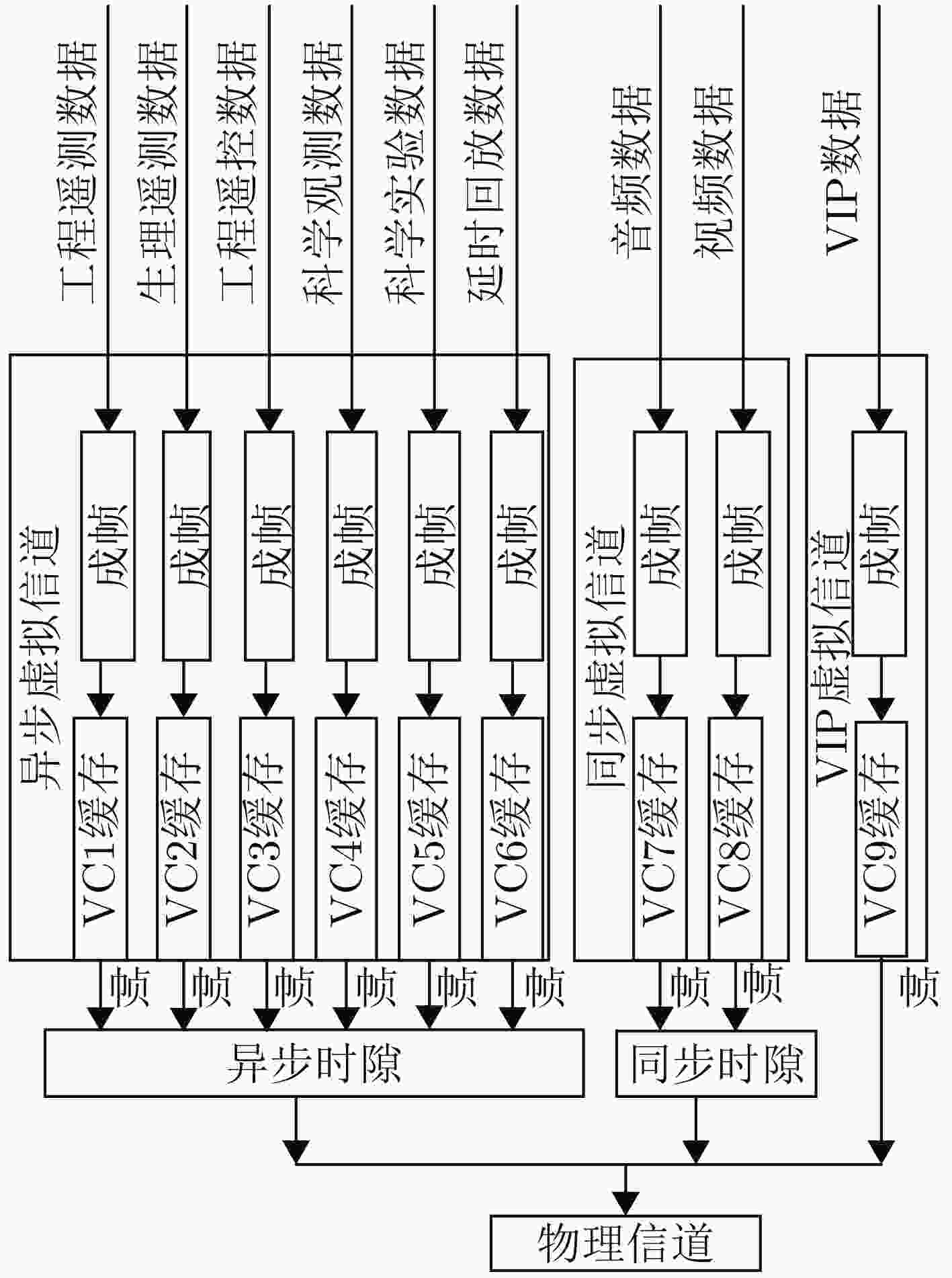
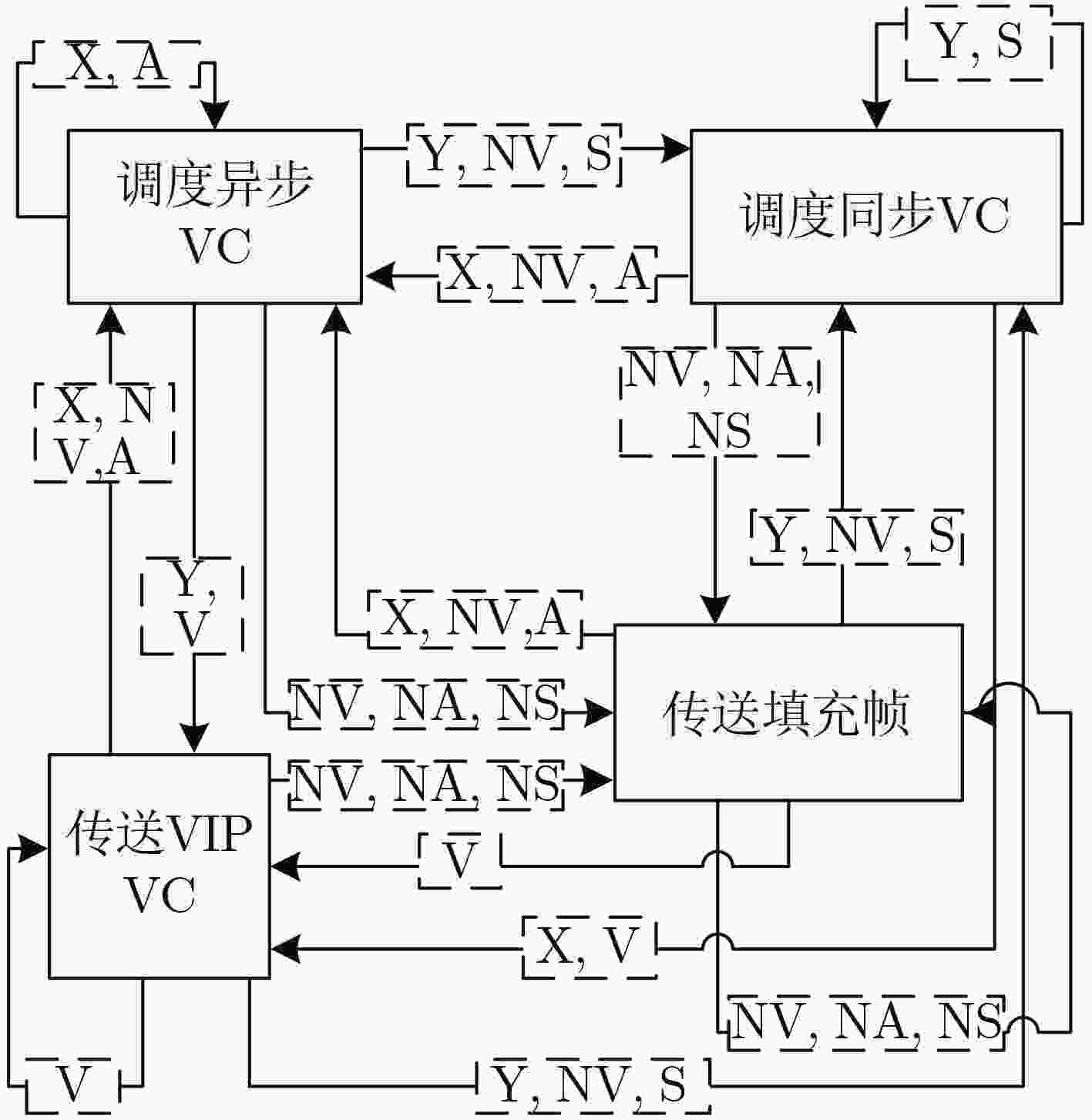
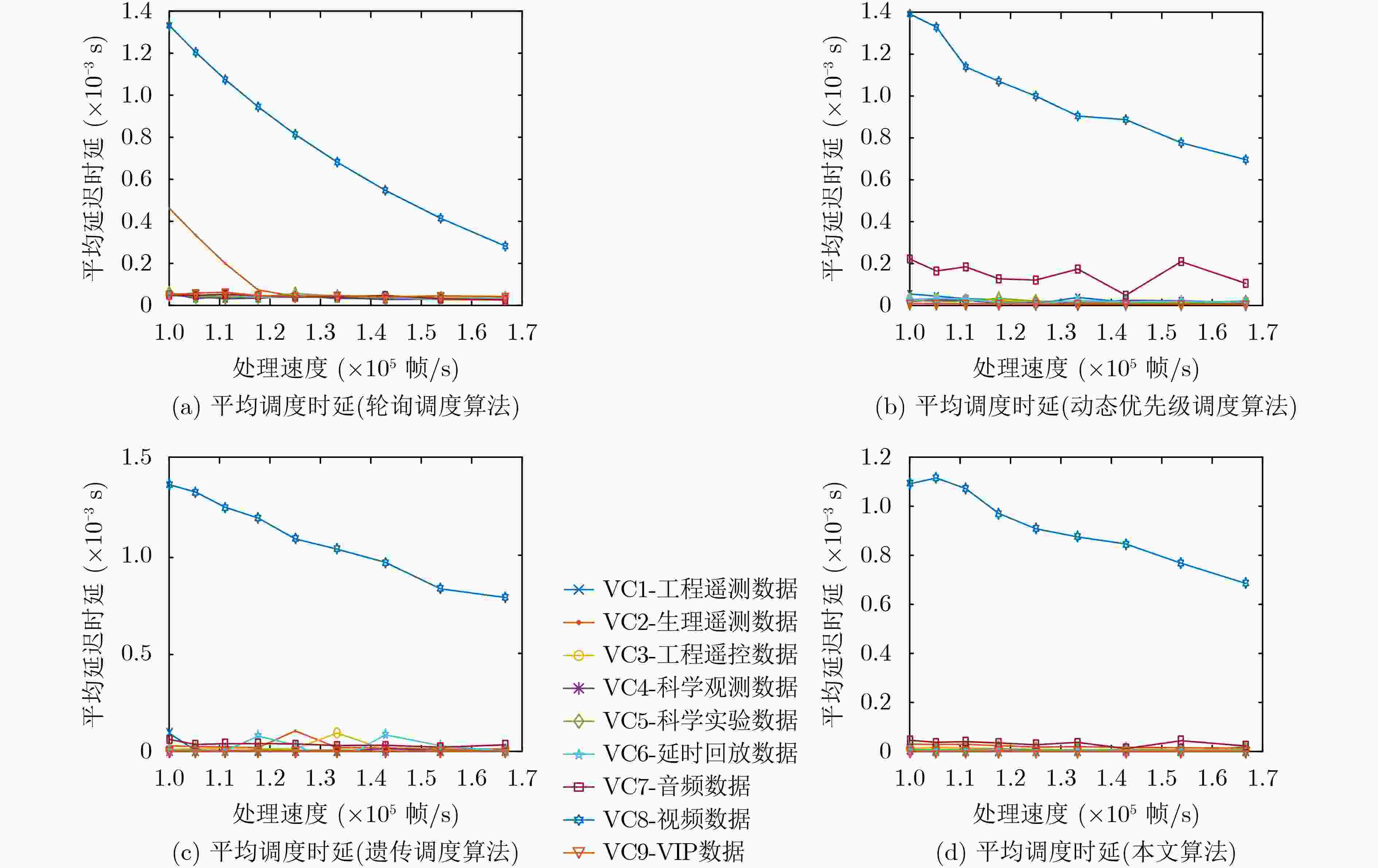
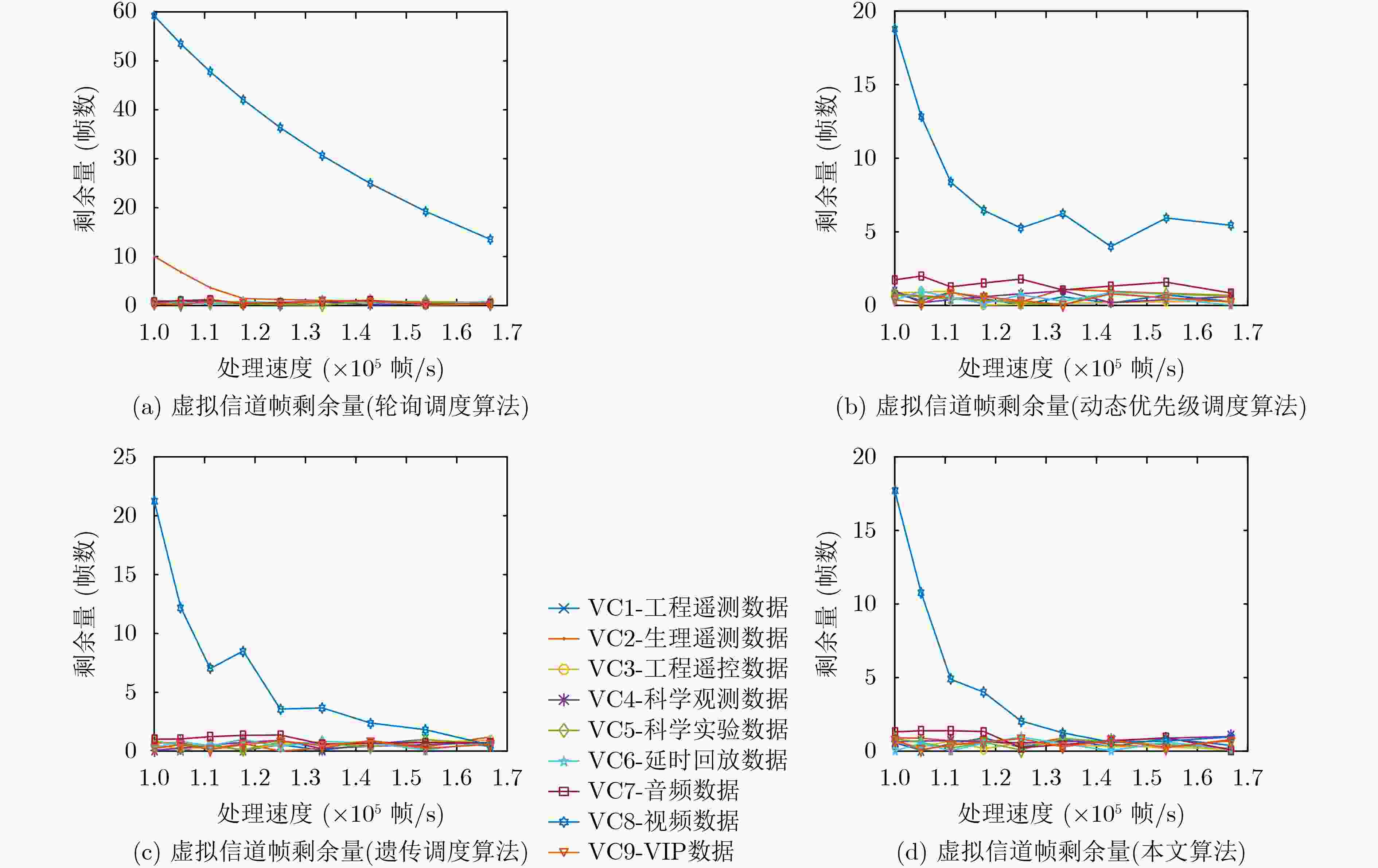
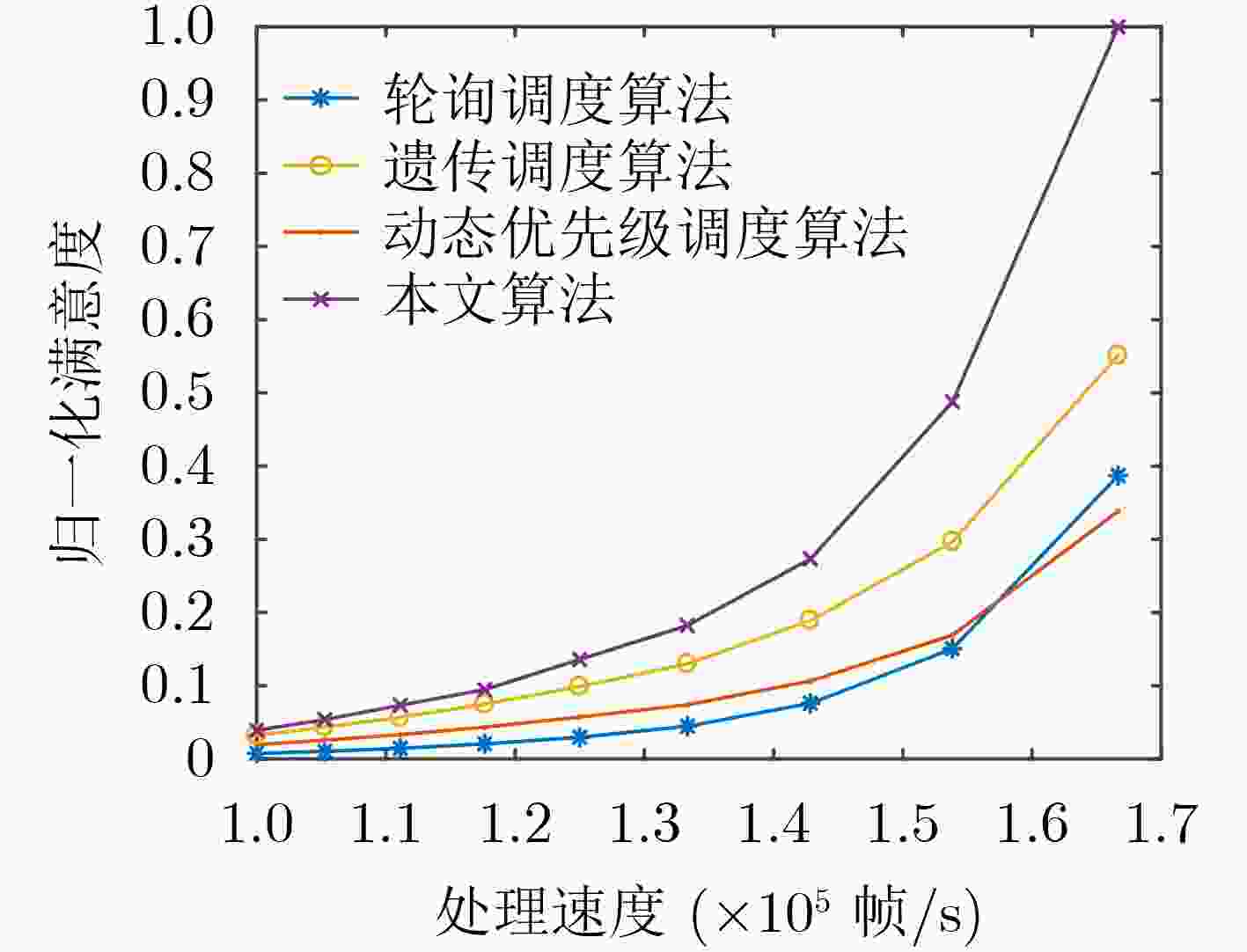
摘要: 为高效传输业务类型多样化的空间数据,该文基于高级在轨系统(AOS)虚拟信道复用技术,建立了AOS虚拟信道(VC)混合调度模型。在混合调度模型中,对异步虚拟信道提出了基于遗传-粒子群排序的调度算法,业务优先级、调度时延紧迫度及帧剩余量紧迫度是影响虚拟信道调度先后顺序的关键约束,该算法根据约束建立了遗传-粒子群适应度函数模型,进一步使粒子群体内的粒子根据遗传算法的进化算子进行位置更新,从而找到最优的异步虚拟信道调度顺序。同时,对同步虚拟信道设计了动态加权轮询调度算法,使各同步虚拟信道按照加权因子和分配的时隙数,轮流占用物理信道。仿真结果表明,该文的虚拟信道混合调度算法兼顾了异步数据的优先性、同步数据的等时性和VIP数据的紧迫性,具有更小的平均调度时延和更少的帧剩余量,满足不同业务的传输要求。Abstract: In view of transporting various spatial data service types, an Advanced Orbiting Systems (AOS) virtual channel hybrid scheduling model is established based on AOS virtual channel multiplexing technology. In the model, a algorithm based on genetic-particle swarm ordering is proposed for asynchronous Virtual Channel (VC). Service priority, scheduling delay urgency and frame remaining urgency are the key constraints that affect the scheduling order of VC.The algorithm establishes the genetic-particle swarm fitness function model according to the constraints, and further enables the particles in the particle swarm to update the position according to the evolution operator of the genetic algorithm, thereby finding the optimal asynchronous VC scheduling sequence.At the same time, a dynamic weighted round-robin scheduling algorithm is designed for the synchronous VC, so that each synchronous VC occupies the physical channel according to the weighting factor and the allocated number of time slots. Simulation results show that the VC hybrid scheduling algorithm in this paper takes into account the priority of asynchronous data, the isochronism of synchronous data, and the urgency of VIP data. It has a smaller average scheduling delay and less frame remaining, so the algorithm meets the transmission requirements of different services.
-
表 1 算法1:遗传-粒子群排序过程
输入:粒子个数$N$,粒子维度$n$,粒子位置更新次数$D$,粒子初
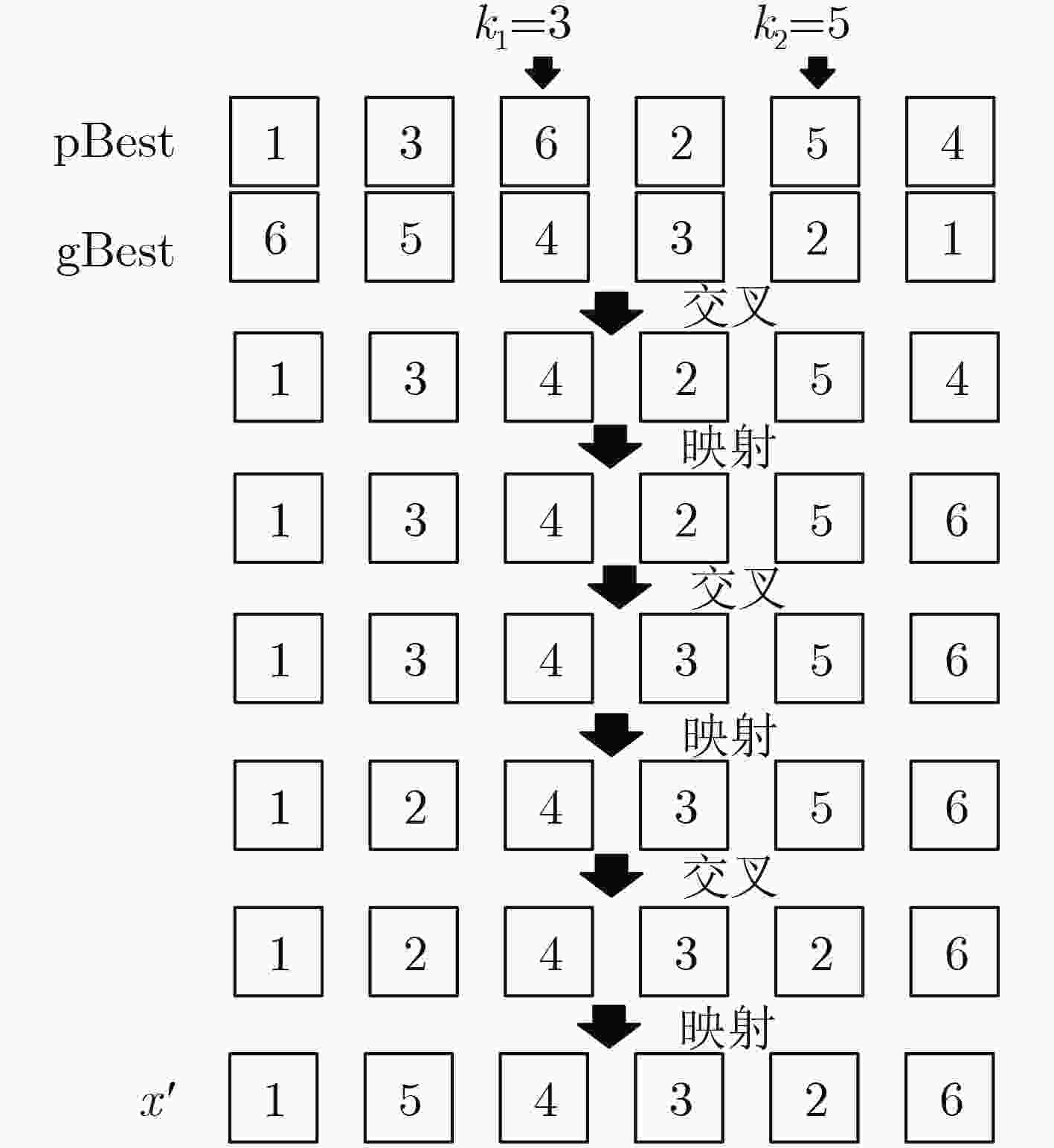
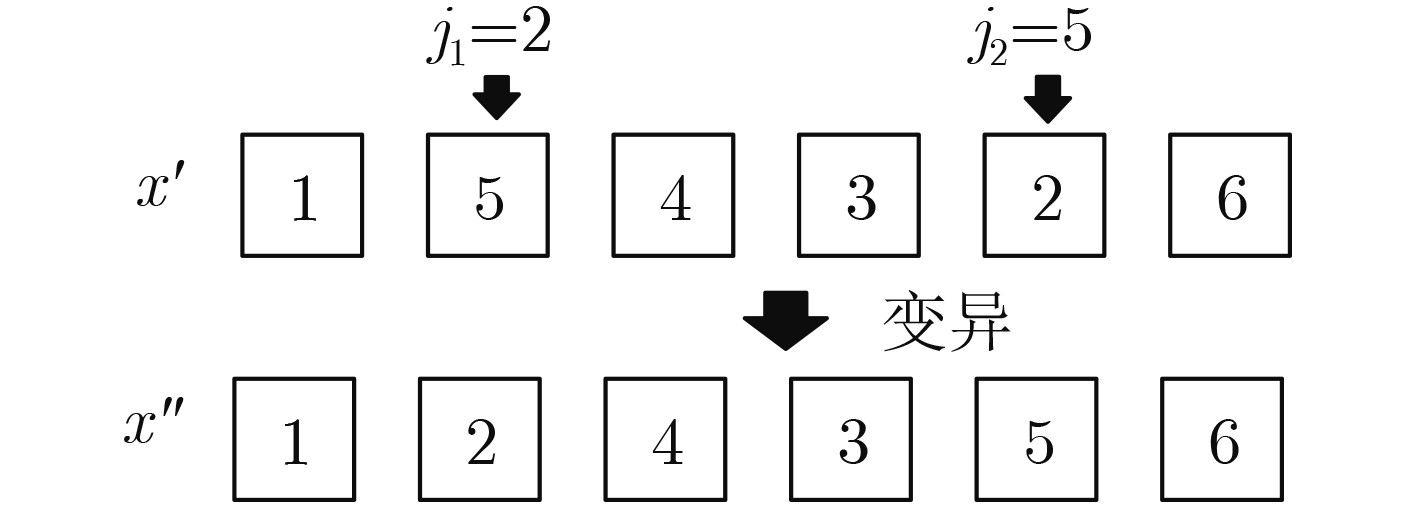
始位置${{x}}$输出:粒子群最优位置gBest (1) 粒子当前最好位置${\rm{pBest}} = {{x}}$ (2) 根据式(7)计算粒子适应度函数值$f$ (3) for i=1 to $N$ do (4) 粒子个体最优值$p(i) = f(i)$ (5) end for (6) 粒子群最优值$g = \min (f(i))$ (7) for l=1 to $D$ do (8) for m=1 to $N$ do (9) 执行遗传-粒子群进化算子:交叉、变异、选择,更新粒子位置 (10) end for (11) 根据式(7)计算位置更新后粒子的适应度函数值$f$ (12) for m=1 to $N$ do (13) if $f(m) < p(m)$ then (14) 粒子个体最优值$p(m) = f(m)$ (15) end if (16) if $p(m) < g$ then (17) 粒子群最优值$g = p(m)$ (18) end if (19) end for (20) end for (21) 粒子群最优位置${gBest}$即为粒子群最优值$g$对应的位置向量 表 2 算法2:异步虚拟信道调度过程
输入:各异步VC优先级${p_i}$,平均调度时延${t_{ {{{\rm{avg}}\_{\rm{delay}}\_i} } } }$,帧剩余量${R_{{\rm{ES}}i}}$,一个调度周期内异步VC总时隙数${T_a}$ 输出:各异步VC平均调度时延${t_{ {{{\rm{avg}}\_{\rm{delay}}\_i} } } }$,帧剩余量${R_{{\rm{ES}}i}}$ (1) if 是异步时隙 then (2) if 存在某一VC帧剩余量${R_{ {\rm{ES} }i } } \ge 1$ then (3) 调用算法1得出粒子群最优位置${ {{\rm{gBest}}} }$即各VC最佳调度顺序 (4) 将帧剩余量大于等于1的VC按${ {{\rm{gBest}}} }$中的顺序重新排列 (5) 按照新的顺序进行调度 (6) 计算各异步VC平均调度时延${t_{ {{{\rm{avg}}\_{\rm{delay}}\_i} } } }$,帧剩余量${R_{{\rm{ES}}i}} $ (7) end if (8) end if 表 3 虚拟信道参数
虚拟信道 业务类型 优先级 允许最大调度延时(s) 平均包到达率(包/s) 平均帧到达率(帧/s) VC1 工程遥测数据 5 0.0100 17.1500×103 1.7150×103 VC2 生理遥测数据 2 0.0020 24.7600×103 12.3750×103 VC3 工程遥控数据 6 0.0500 15.1440×103 7.5720×103 VC4 科学观测数据 4 0.0070 31.9100×103 3.1910×103 VC5 科学实验数据 3 0.0020 45.5100×103 4.5510×103 VC6 延时回放数据 1 0.0015 12.8560×103 1.6070×103 VC7 音频数据 – – 5.9900×103 2.9950×103 VC8 视频数据 – – 40.5300×103 20.2650×103 VC9 VIP数据 – – – 0.9550×103 -
[1] ZHANG Cuitao and HE Xiongwen. Research and application of consultative committee for space data systems wireless communications standards for spacecraft[J]. World Academy of Science, Engineering and Technology International Journal of Electronics and Communication Engineering, 2017, 11(11): 1148–1151. [2] 戴昌昊, 张德智, 胡倩, 等. 一种基于CCSDS AOS协议的分包遥测调度算法[J]. 测控技术, 2017, 36(9): 47–49, 53. doi: 10.3969/j.issn.1000-8829.2017.09.011DAI Changhao, ZHANG Dezhi, HU Qian, et al. A packet telemetry scheduling algorithm based on CCSDS AOS protocol[J]. Measurement &Control Technology, 2017, 36(9): 47–49, 53. doi: 10.3969/j.issn.1000-8829.2017.09.011 [3] CCSDS. CCSDS 732.0-B-2 AOS space data link protocol[S]. Washington, USA: CCSDS, 2006: 7. [4] CCSDS. CCSDS 912.3-B-2 Space link extension—forward space packet service specification[S]. Washington, USA: CCSDS, 2010. [5] LIU Qingli, PAN Chengsheng, WANG Guoren, et al. CCSDS advanced orbiting systems, data links protocol: Study on virtual channels scheduling algorithm[C]. The 2008 8th IEEE International Conference on Intelligent Systems Design and Applications, Kaohsiung, China, 2008: 351–355. doi: 10.1109/ISDA.2008.158. [6] RIHA A P and OKINO C. An advanced orbiting systems approach to quality of service in space-based intelligent communication networks[C]. 2006 IEEE Aerospace Conference, Big Sky, USA, 2006: 1–11. doi: 10.1109/AERO.2006.1655837. [7] 刘立士, 李清凡, 田野, 等. 基于帧紧迫度的边界可移动虚拟信道调度算法[J]. 科学技术与工程, 2014, 14(17): 97–103. doi: 10.3969/j.issn.1671-1815.2014.17.019LIU Lishi, LI Qingfan, TIAN Ye, et al. A virtual channels scheduling algorithm of moving boundary based on frame urgency[J]. Science Technology and Engineering, 2014, 14(17): 97–103. doi: 10.3969/j.issn.1671-1815.2014.17.019 [8] GUPTA I, KUMAR M S, JANA P K. Efficient workflow scheduling algorithm for cloud computing system: A dynamic priority-based approach[J]. Arabian Journal for Science and Engineering, 2018, 43(12): 7945–7960. doi: 10.1007/s13369-018-3261-8 [9] 季伟东, 孙小晴, 林平, 等. 基于非线性降维的自然计算方法[J]. 电子与信息学报, 2020, 42(8): 1982–1989. doi: 10.11999/JEIT190623JI Weidong, SUN Xiaoqing, LIN Ping, et al. Natural computing method based on nonlinear dimension reduction[J]. Journal of Electronics &Information Technology, 2020, 42(8): 1982–1989. doi: 10.11999/JEIT190623 [10] JIA Zhaohong, WANG Yan, WU Chao, et al. Multi-objective energy-aware batch scheduling using ant colony optimization algorithm[J]. Computers & Industrial Engineering, 2019, 131: 41–56. [11] MARINI F and WALCZAK B. Particle Swarm Optimization (PSO). A tutorial[J]. Chemometrics and Intelligent Laboratory Systems, 2015, 149: 153–165. [12] ZHANG Yudong, WANG Shuihua, and JI Genlin. A comprehensive survey on particle swarm optimization algorithm and its applications[J]. Mathematical Problems in Engineering, 2015, 2015: 931256. [13] 唐红亮, 吴柏林, 胡旺, 等. 基于粒子群优化的地震应急物资多目标调度算法[J]. 电子与信息学报, 2020, 42(3): 737–745. doi: 10.11999/JEIT190277TANG Hongliang, WU Bolin, HU Wang, el al. Earthquake emergency resource multiobjective schedule algorithm based on particle swarm optimization[J]. Journal of Electronics &Information Technology, 2020, 42(3): 737–745. doi: 10.11999/JEIT190277 [14] 唐巍, 高峰. 考虑用户满意度的户用型微电网日前优化调度[J]. 高电压技术, 2017, 43(1): 140–148.TANG Wei and GAO Feng. Optimal operation of household microgrid day-ahead energy considering user satisfaction[J]. High Voltage Engineering, 2017, 43(1): 140–148. [15] 刘经浩, 贺蓉, 李仁发, 等. 一种基于实时电价的HEMS家电最优调度方法[J]. 计算机应用研究, 2015, 32(1): 132–137, 160. doi: 10.3969/j.issn.1001-3695.2015.01.030LIU Jinghao, HE Rong, LI Renfa, et al. Optimal scheduling model for home energy management system based on real-time electricity pricing[J]. Application Research of Computers, 2015, 32(1): 132–137, 160. doi: 10.3969/j.issn.1001-3695.2015.01.030 -





 下载:
下载:


 下载:
下载:
