Integral Cryptanalysis of ACE Encryption Algorithm
-
摘要: ACE是国际轻量级密码算法标准化征集竞赛第2轮候选算法之一。该算法具有结构简洁,软硬件实现快、适用于资源受限环境等特点,其安全性备受业界广泛关注。该文引入字传播轨迹新概念,构建了一个传播轨迹的描述模型,并给出一个可以自动化评估分组密码算法抵抗积分攻击能力的方法。基于ACE算法结构特点,将该自动化搜索方法应用于评估ACE算法的安全性。结果表明:ACE置换存在12步的积分区分器,需要的数据复杂度为2256,时间复杂度为2256次12步的ACE置换运算,存储复杂度为8 Byte。相比于ACE算法设计者给出的积分区分器,该新区分器的步数提高了4步。Abstract: ACE as an authenticated encryption algorithm is selected as one of the round 2 candidates of the lightweight crypto standardization process. Since its excellent design advantages, e.g. simple structure, high performance in software and hardware, and suitable for constrained environments, the security of ACE is received extensive attention. In this paper, the concept of word propagation trail is introduced, and an exact model is constructed to describe the trail. A new automatic method for evaluating the security of word-based cipher against the integral attack is also proposed by using this model. Moreover, based on the structure of ACE, the security of ACE permutation is evaluated by using this new automatic method. More specifically, a new 12-step integral distinguisher of ACE permutation is verified by using this method, which requires the data complexity of about 2256 chosen data, the time complexity of about 2256 12-step ACE permutation operations, and the memory complexity of about 8 Byte. Compared with the distinguishers given by ACE’s designer, this new result prominently increases 4 steps indeed.
-
表 1 文中用到的符号
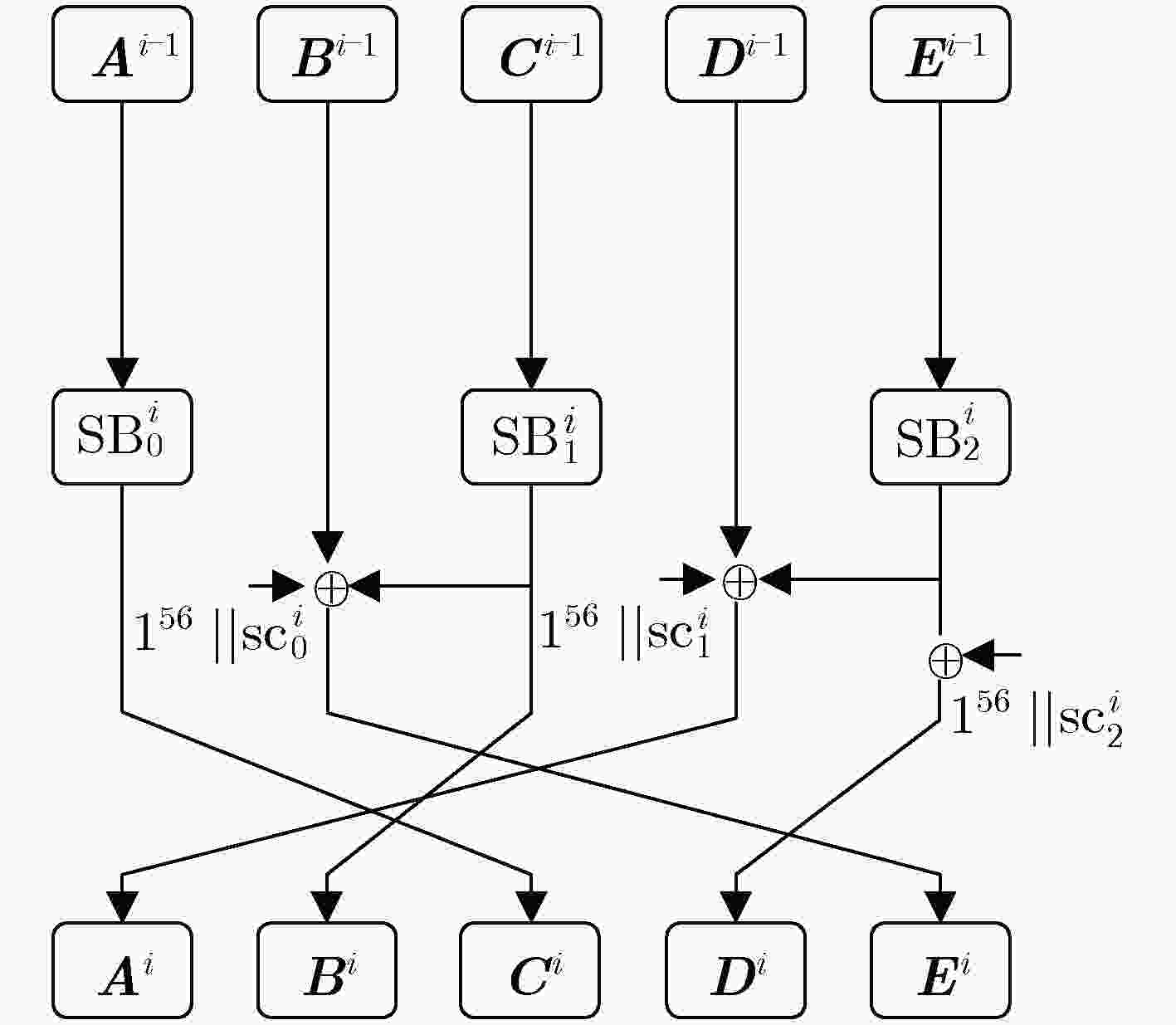
符号 定义 ${{X}} \oplus {{Y}}$ 表示${{X}}$和${{Y}}$之间按位异或 +/– 十进制加/减 ${{X}}||{{Y}}$ 表示${{X}}$和${{Y}}$串联 ${1^n}/{0^n}$ 表示$n$ bit全1或全0的比特串 ${\rm{SB}}_j^i({{X}})$ 表示ACE置换第$i$步的第$j$个密码S盒 ${\rm{|}}{{X}}{\rm{|}}$ 表示集合${{X}}$中元素的个数 $(\alpha ,{{\beta }}) = \max (x[0],x[1], ··· ,x[n - 1])$ 计算数组$[x[0],x[1], ··· ,x[n - 1]]$的最大值$\alpha $以及最大值对应的下标的集合${{\beta }}$,例如$\max (2,2,1,0) = (2,[0,1])$ $\alpha = {\max '}(x[0],x[1], ··· ,x[n - 1])$ 计算数组$[x[0],x[1], ··· ,x[n - 1]]$中的最大值$\alpha $ $(\alpha ,{{\beta }}) = \min (x[0],x[1], ··· ,x[n - 1])$ 计算数组$[x[0],x[1] ··· ,x[n - 1]]$的最小值$\alpha $以及最小值对应的下标的集合${{\beta }}$,例如$\min (2,2,1,0) = (0,[3])$ $\alpha = {\min'}(x[0],x[1], ··· ,x[n - 1])$ 计算数组$[x[0],x[1], ··· ,x[n - 1]]$的最小值$\alpha $ 表 2 算法1:利用字传播模型确定
$r_{\rm{e}}^k$ 输入:分组密码轮函数${f_{\rm{r}}} \in {(F_2^n)^m}$,加密轮数$R$,活跃字的下标$k$ 输出:$r_{\rm{e}}^k$,以及加密$r_{\rm{e}}^k$轮后,当第$k$个字活跃时,输出状态中的平衡字的下标集合${{{\omega }}_k}$ (1) ${r_{\rm{h}}} = R$, ${r_{\rm{l}}} = 0$, $r_{\rm{e}}^k = 0$, $r = 0$, flag= 0 (2) $x_k^i[0]$, $x_k^i[1]$, $ ··· $, $x_k^i[m - 1]$为$i$轮加密后,输出状态对应的MILP模型变量,每一个MILP变量的值范围是大于等于0的整数 (3) While ${r_{\rm{h}}} - {r_{\rm{l}}} > 1$ do (4) $r = \left\lfloor {({r_{\rm{h}}} + {r_{\rm{l}}})/2} \right\rfloor $ (5) 利用性质3和性质4构建出$r$轮的字传播模型${M_{\rm{e}}}$ (6) ${M_{\rm{e}}}.{\rm{con}} \leftarrow x_k^0[k] = 1,M.{\rm{con}} \leftarrow x_k^0[j] = 0,j \in [0,m), j \ne k$ (7) ${M_{\rm{e}}}.{\rm{con}} \leftarrow {\min' }\{ (x_k^r[0],x_k^r[1], \cdots ,x_k^r[m - 1])\} = 1$ (8) 利用求解器对模型${M_{\rm{e}}}$进行求解 (9) If Me 有解 (10) ${r_{\rm{l}}} = r,{\rm{ flag }} = 1$ (11) else (12) ${r_{\rm{h}}} = r,{\rm{ flag}} = 0$ (13) End If (14) End While (15) If ${\rm{flag}} = = 1$ (16) $r_{\rm{e}}^k = r$ (17) else (18) $r_{\rm{e}}^k = r - 1$ (19)End If (20)$(1,{{{\omega }}_k}) = \min \{ (x_k^{r_{\rm{e}}^k}[0],x_k^{r_{\rm{e}}^k}[1], \cdots ,x_k^{r_{\rm{e}}^k}[m - 1])\} $ (21) return $r_{\rm{e}}^k$和${{{\omega }}_k}$ 表 3 算法2:利用字传播模型确定
$r_{\rm{d}}^k$ 输入:分组密码解密轮函数${f_{\rm{r}}}^{ - 1} \in {(F_2^n)^m}$,解密轮数$R$,活跃字的下标$k$ 输出:$r_{\rm{d}}^k$,以及解密$r_{\rm{d}}^k$轮后,输出状态中的不包含第$k$个字的下标集合${{{\varphi }}_k}$ (1) ${r_{\rm{h}}} = R$, ${r_{\rm{l}}} = 0$, $r_{\rm{d}}^k = 0$, $r = 0$, ${\rm{flag}} = 0$ (2) $y_k^i[0]$, $y_k^i[1]$, $ ··· $, $y_k^i[m - 1]$为第$i$轮解密输出状态对应的MILP模型变量,每一个MILP变量的值范围是大于等于0的整数 (3) While ${r_{\rm{h}}} - {r_{\rm{l}}} > 1$ do (4) $r = \left\lfloor {({r_{\rm{h}}} + {r_{\rm{l}}})/2} \right\rfloor $ (5) 利用性质3和性质4构建出$r$轮的字解密传播模型${M_{\rm{d}}}$ (6) ${M_{\rm{d}}}.{\rm{con}} \leftarrow y_k^0[k] = 1,M.{\rm{con}} \leftarrow y_k^0[j] = 0,j \in [0,m),j \ne k$ (7) ${M_{\rm{d}}}.{\rm{con}} \leftarrow {\min '}\{ (y_k^r[0],y_k^r[1], ··· ,y_k^r[m - 1])\} = 0$ (8) 利用求解器对模型${M_{\rm{d}}}$进行求解 (9) If Md 有解 (10) ${r_{\rm{l}}} = r,{\rm{ flag }} = 1$ (11) else (12) ${r_{\rm{h}}} = r,{\rm{ flag}} = 0$ (13) End If (14) End While (15) If ${\rm{flag}} = = 1$ (16) $r_{\rm{d}}^k = r$ (17) else (18) $r_{\rm{d}}^k = r - 1$ (19) End If (20) $(0,{{{\varphi }}_k}) = \min \{ (y_k^{r_{\rm{d}}^k}[0],y_k^{r_{\rm{d}}^k}[1], ··· ,y_k^{r_{\rm{d}}^k}[m - 1])\} $ (21) return $r_{\rm{d}}^k$和${{{\varphi }}_k}$ 表 4 ACE置换对应的
$r_{\rm{e}}^k$ 和${{{\omega }}_k}$ $k$ $r_{\rm{e}}^k$ ${{{\omega }}_k}$ 0 8 [1] 1 8 [3] 2 7 [1] 3 9 [1] 4 7 [3] 表 5 ACE置换对应的
$r_{\rm{d}}^k$ 和${{{\varphi }}_k}$ $k$ $r_{\rm{d}}^k$ ${{{\varphi }}_k}$ 0 4 [0] 1 3 [4] 2 5 [0] 3 3 [0] 4 4 [4] 表 6 ACE置换12步的积分区分器
输入形式 输出形式 ${c^{64}}{a^{64}}{a^{64}}{a^{64}}{a^{64}}$ ${u^{64}}{b^{64}}{u^{64}}{u^{64}}{u^{64}}$ 注:${c^{64}}$表示任意的一个64 bit的常数,${a^{64}}$表示64 bit的活跃字集,${b^{64}}$表示64 bit的平衡字集,${u^{64}}$表示64 bit的未知字集。 表 7 ACE置换积分分析结果对比
分析方法 积分区分器步数 选择明文量 方法 除属性 8 ${2^{319}}$ 文献[19] 字传播轨迹 12 ${2^{256}}$ 本文 -
MATSUI M. Linear cryptanalysis method for DES cipher[C]. Workshop on the Theory and Application of Cryptographic Techniques on Advances in Cryptology, Lofthus, Norway, 1993: 386–397. doi: 10.1007/3-540-48285-7_33. BIHAM E and SHAMIR A. Differential cryptanalysis of DES-like cryptosystems[J]. Journal of Cryptology, 1991, 4(1): 3–72. doi: 10.1007/BF00630563 BIHAM E, BIRYUKOV A, and SHAMIR A. Cryptanalysis of Skipjack reduced to 31 rounds using impossible differentials[C]. International Conference on the Theory and Application of Cryptographic Techniques Prague on Advances in Cryptology, Prague, Czech Republic, 1999: 12–23. doi: 10.1007/3-540-48910-X_2. 韦永壮, 史佳利, 李灵琛. LiCi分组密码算法的不可能差分分析[J]. 电子与信息学报, 2019, 41(7): 1610–1617. doi: 10.11999/JEIT180729WEI Yongzhuang, SHI Jiali, and LI Lingchen. Impossible differential cryptanalysis of LiCi block cipher[J]. Journal of Electronics &Information Technology, 2019, 41(7): 1610–1617. doi: 10.11999/JEIT180729 DINUR I and SHAMIR A. Cube attacks on tweakable black box polynomials[C]. The 28th Annual International Conference on the Theory and Applications of Cryptographic Techniques on Advances in Cryptology, Cologne, Germany, 2009: 278–299. doi: 10.1007/978-3-642-01001-9_16. KNUDSEN L and WAGNER D. Integral cryptanalysis[C]. The 9th International Workshop on Fast Software Encryption, Leuven, Belgium, 2002: 112–127. doi: 10.1007/3-540-45661-9_9. TODO Y. Structural evaluation by generalized integral property[C]. The 34th Annual International Conference on the Theory and Applications of Cryptographic Techniques on Advances in Cryptology, Sofia, Bulgaria, 2015: 287–314. doi: 10.1007/978-3-662-46800-5_12. LI Yanjun, WU Wenling, and ZHANG Lei. Improved integral attacks on reduced-round CLEFIA block cipher[C]. The 12th International Workshop on Information Security Applications, Jeju Island, Korea, 2011: 28–39. doi: 10.1007/978-3-642-27890-7_3. Z’ABA M R, RADDUM H, HENRICKSEN M, et al. Bit-Pattern based integral attack[C]. The 15th International Workshop on Fast Software Encryption, Lausanne, Switzerland, 2008: 363–381. doi: 10.1007/978-3-540-71039-4_23. LIU Meicheng. Degree evaluation of NFSR-based cryptosystems[C]. The 37th Annual International Cryptology Conference on Advances in Cryptology, Santa Barbara, USA, 2017: 20–24. doi: 10.1007/978-3-319-63697-9_8. BOURA C, CANTEAUT A, and DE CANNIÈRE C. Higher-order differential properties of KECCAK and LUFFA[C]. The 18th International Workshop on Fast Software Encryption, Lyngby, Denmark, 2011: 252–269. doi: 10.1007/978-3-642-21702-9_15. TODO Y and MORII M. Bit-based division property and application to SIMON family[C]. The 23rd International Workshop on Fast Software Encryption, Bochum, Germany, 2016: 357–377. doi: 10.1007/978-3-662-52993-5_18. XIANG Zejun, ZHANG Wentao, BAO Zhenzhen, et al. Applying MILP method to searching integral distinguishers based on division property for 6 lightweight block ciphers[C]. The 22nd International Conference on the Theory and Application of Cryptology and Information Security on Advances in Cryptology, Hanoi, Vietnam, 2016: 648–678. doi: 10.1007/978-3-662-53887-6_24. WANG Senpeng, HU Bin, GUAN Jie, et al. MILP-aided method of searching division property using three subsets and applications[C]. The 25th International Conference on the Theory and Application of Cryptology and Information Security on Advances in Cryptology, Kobe, Japan, 2019: 398–427. doi: 10.1007/978-3-030-34618-8_14. ESKANDARI Z, KIDMOSE A B, KÖLBL S, et al. Finding integral distinguishers with ease[C]. The 25th International Conference on Selected Areas in Cryptography, Calgary, Canada, 2018: 115–138. doi: 10.1007/978-3-030-10970-7_6. ZHANG Wenying and RIJMEN V. Division cryptanalysis of block ciphers with a binary diffusion layer[J]. IET Information Security, 2019, 13(2): 87–95. doi: 10.1049/iet-ifs.2018.5151 徐洪, 方玉颖, 戚文峰. SIMON64算法的积分分析[J]. 电子与信息学报, 2020, 42(3): 720–728. doi: 10.11999/JEIT190230XU Hong, FANG Yuying, and QI Wenfeng. Integral attacks on SIMON64[J]. Journal of Electronics &Information Technology, 2020, 42(3): 720–728. doi: 10.11999/JEIT190230 ZHANG Wenying, CAO Meichun, GUO Jian, et al. Improved security evaluation of SPN block ciphers and its applications in the single-key attack on SKINNY[J]. IACR Transactions on Symmetric Cryptology, 2020, 2019(4): 171–191. doi: 10.13154/tosc.v2019.i4.171-191 AAGAARD M, ALTAWY R, GONG Guang, et al. ACE: An authenticated encryption and hash algorithm[EB/OL]. https://uwaterloo.ca/communications-security-lab/lwc/ace, 2020. Computer Security Resource Center. Lightweight cryptography[EB/OL]. https://csrc.nist.gov/Projects/lightweight-cryptography, 2020. BOGDANOV A and SHIBUTANI K. Generalized Feistel networks revisited[J]. Designs, Codes and Cryptography, 2013, 66(1): 75–97. doi: 10.1007/s10623-012-9660-z YANG Gangqiang, ZHU Bo, SUDER V, et al. The SIMECK family of lightweight block ciphers[C]. The 17th International Workshop on Cryptographic Hardware and Embedded Systems, Saint-Malo, France, 2015: 307–329. doi: 10.1007/978-3-662-48324-4_16. -





 下载:
下载:








 下载:
下载:
