Off Line Fingerprint Database Based on Multivariate Gaussian Mixture Model
-
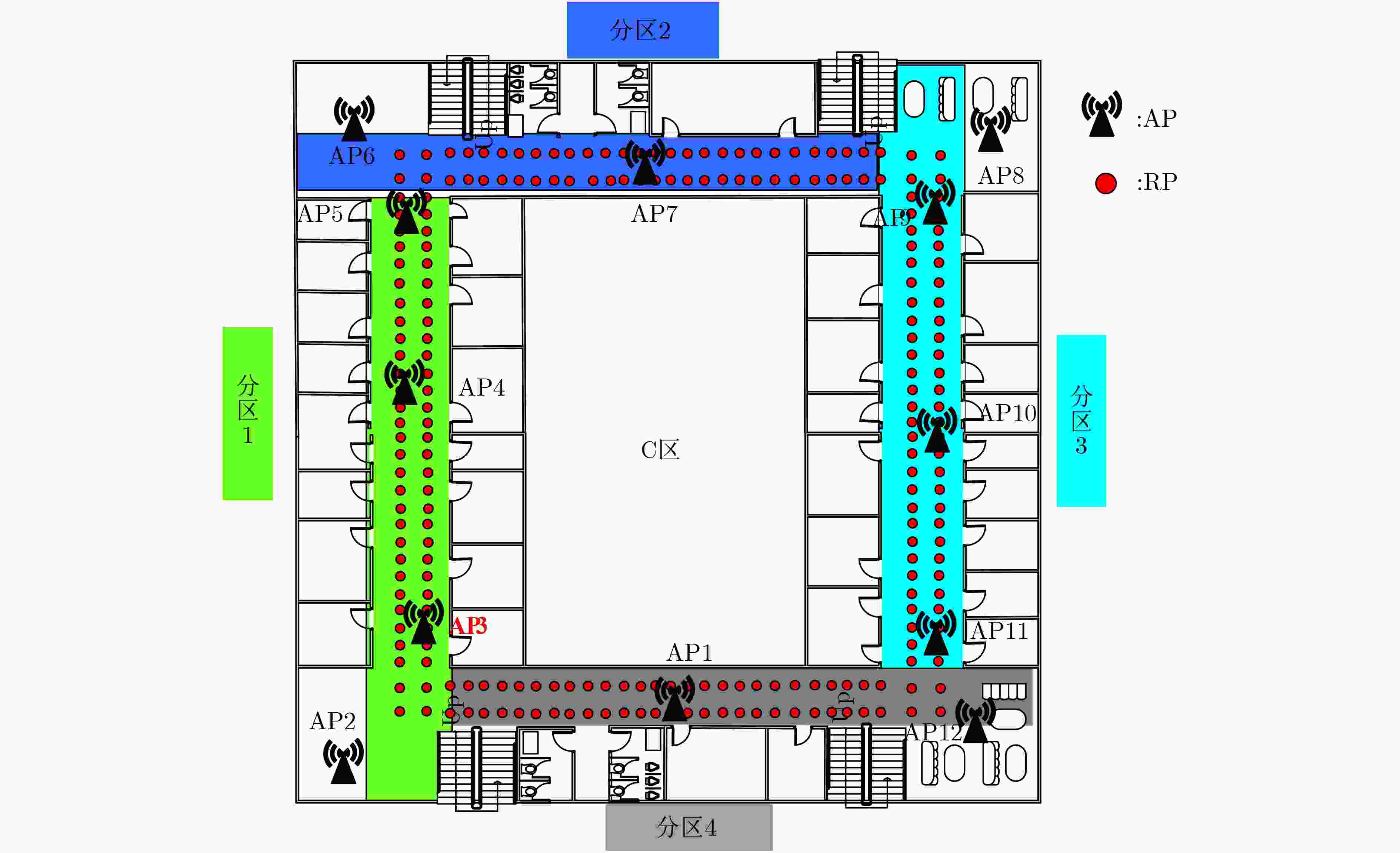
摘要: 针对室内环境下单次采样测量值的波动变化及信号间的相互干扰,该文提出一种基于分区多元高斯混合模型(MVGMM)的室内定位系统。根据信号接入点(AP)铺设位置与空间结构,系统采用一对多支持向量机算法对目标区域做分区操作,以精确信号变化的区域范围。利用狭小分区内信号间的耦合关系,建立基于信号间相互干扰的多元高斯混合模型,以改善信号波动所造成的定位精度下降。当室内环境发生变化时,基于分区多元高斯混合模型的自适应更新算法可对各分区指纹数据的可信度做出判断,并以自适应算法更新信号波动较大分区的模型参数,提高模型与现有环境间的耦合程度。实验结果表明,该文算法可利用相对少量样本数据,构建稳定可维护的室内信号分布模型,相较于其他算法,其定位精度也有一定程度提高。Abstract: For the fluctuation of single sampling measurement value and the mutual interference between signals in indoor environment, this paper proposes an indoor positioning system based on the partition MultiVariate Gaussian Mixture Model(MVGMM). According to the Access Point (AP) position and indoor spatial structure, the system uses SVM classification in “one-against-all” form to partition the target area in order to predict the subarea with signal changes. A MVGMM based on the mutual interference between signals is established by using the coupling relationship between multiple communication devices in the partition. It is important to improve the positioning accuracy which is affected by signal fluctuation. When the indoor environment changes, the adaptive updating algorithm based on the partition MVGMM can test the reliability of fingerprint data in each segmentation. Moreover, it can update the model parameters in the partition with large signal fluctuation by the adaptive algorithm to strengthen the coupling relationship between the model and the existing environment. Experimental result demonstrates that the proposed algorithm can build a stable and maintainable indoor signal distribution model by using a relatively small number of sample data. Its positioning accuracy is also improved to a certain extent compared to other algorithms.
-
表 1 MVGMM模型的参数估计
输入:高斯组成元素数量${C_k}$,高斯组成元素的初始权值$\bar w_c^k$,初始均值${\bar{{\mu }}}_c^k$,初始协方差${\bar{{ P}}}_c^k$,分区${\varOmega _k}$内参考点位置${ {{x} }^k} = [{{x} }_1^k,{{x} }_2^k,···,{{x} }_{ {N_k} }^k]$
与相应采样值${{{R}}^k} = [{{r}}_1^k,{{r}}_2^k,···,{{r}}_{{N_k}}^k]$, $c \in \{ 1,2,..,{C_k}\} $输出:高斯组成元素权值$w_c^k$,均值${{\mu }}_c^k$,协方差${{P}}_c^k$ do $w_c^k \leftarrow \bar w_c^k$, ${{\mu }}_c^k \leftarrow {\bar{{\mu }}}_c^k$, ${{P}}_c^k \leftarrow {\bar{{ P}}}_c^k$ E步: for $n \in \{ 1,2,···,{N_k}\} ,c \in \{ 1,2,..,{C_k}\} $ 计算$\gamma _{n,c}^k$ //基于式(5) end M步: for $c \in \{ 1,2,..,{C_k}\} $ 计算${w_c}$, ${{\mu }}_c^k$, ${{P}}_c^k$ //基于式(6)—式(8) end while ($(L({{\bar{{z}}}^k},{{\bar{{w}}}^k},{{\bar{{\mu }}}^k},{{\bar{{ P}}}^k}) - L({{{z}}^k},{{{w}}^k},{{{\mu }}^k},{{{P}}^k})) > 0$) $w_c^k \leftarrow \bar w_c^k$, ${{\mu }}_c^k \leftarrow {\bar{{\mu }}}_c^k$, ${{P}}_c^k \leftarrow {\bar{{ P}}}_c^k$ 表 2 分区MVGMM模型的自适应更新算法
输入:原始高斯组成元素数量${C_k}$,原始高斯组成元素的权值$\hat w_c^k$,均值${\hat{{\mu }}}_c^k$,协方差${\hat{{P}}}_c^k$,新增分区${\varOmega _\kappa }$内采样数据${{\hat{{z}}}^k} = [{\hat{{z}}}_1^k,{\hat{{z}}}_2^k,···,{\hat{{z}}}_{{N_k}}^k]$,
$c \in \{ 1,2,···,{C_k}\} $输出:更新后高斯组成元素权值$w_c^k$,均值${{\mu }}_c^k$,协方差${{P}}_c^k$ do $w_c^k \leftarrow \hat w_c^k$, ${{\mu }}_c^k \leftarrow {\hat{{\mu }}}_c^k$, ${{P}}_c^k \leftarrow {\hat{{P}}}_c^k$ E步: for $n \in \{ 1,2,···,{N_k}\} ,c \in \{ 1,2,···,{C_k}\} $ 计算$\gamma _{n,c}^k$ //基于式(5) end for $c \in \{ 1,2,···,{C_k}\} $ 计算$n_c^k$, $E_c^k({{z}})$和$E_c^k({{{z}}^2})$ //基于式(6)—式(8) 计算${\hat w_c}$, ${\hat{{\mu }}}_c^k$和${\hat{{P}}}_c^k$ //基于式(17)-式(19) end while( $(L({{\hat{{z}}}^k},{{\hat{{w}}}^k},{{\hat{{\mu }}}^k},{{\hat{{P}}}^k}) - L({{{z}}^k},{{{w}}^k},{{{\mu }}^k},{{{P}}^k})) > 0$) $w_c^k \leftarrow \hat w_c^k$,${{\mu }}_c^k \leftarrow {\hat{{\mu }}}_c^k$, ${{P}}_c^k \leftarrow {\hat{{P}}}_c^k$ 表 3 分区判别精度(%)
分区 分区精度(预测正确/测试点) 分区1 99.46(183/184) 分区2 98.91(182/184) 分区3 98.91(182/184) 分区4 99.46(183/184) -
[1] WANG Chun, LUO Juan, and ZHENG Yanliu. Optimal target tracking based on dynamic fingerprint in indoor wireless network[J]. IEEE Access, 2018, 6: 77226–77239. doi: 10.1109/ACCESS.2018.2880247 [2] 江小平, 王妙羽, 丁昊, 等. 基于信道状态信息幅值-相位的被动式室内指纹定位[J]. 电子与信息学报, 2020, 42(5): 1165–1171. doi: 10.11999/JEIT180871JIANG Xiaoping, WANG Miaoyu, DING Hao, et al. Passive fingerprint indoor positioning based on CSI amplitude-phase[J]. Journal of Electronics &Information Technology, 2020, 42(5): 1165–1171. doi: 10.11999/JEIT180871 [3] 左燕, 陈志猛, 蔡立平. 基于约束总体最小二乘的单站DOA/TDOA联合误差校正与定位算法[J]. 电子与信息学报, 2019, 41(6): 1317–1323. doi: 10.11999/JEIT180655ZUO Yan, CHEN Zhimeng, and CAI Liping. Single-observer DOA/TDOA registration and passive localization based on constrained total least squares[J]. Journal of Electronics &Information Technology, 2019, 41(6): 1317–1323. doi: 10.11999/JEIT180655 [4] PATWARI N, HERO A O, PERKINS M, et al. Relative location estimation in wireless sensor networks[J]. IEEE Transactions on Signal Processing, 2003, 51(8): 2137–2148. doi: 10.1109/TSP.2003.814469 [5] 李世宝, 王升志, 刘建航, 等. 基于接收信号强度非齐性分布特征的半监督学习室内定位指纹库构建[J]. 电子与信息学报, 2019, 41(10): 2302–2309. doi: 10.11999/JEIT180599LI Shibao, WANG Shengzhi, LIU Jianhang, et al. Semi-supervised indoor fingerprint database construction method based on the nonhomogeneous distribution characteristic of received signal strength[J]. Journal of Electronics &Information Technology, 2019, 41(10): 2302–2309. doi: 10.11999/JEIT180599 [6] 刘坤, 吴建新, 甄杰, 等. 基于阵列天线和稀疏贝叶斯学习的室内定位方法[J]. 电子与信息学报, 2020, 42(5): 1158–1164. doi: 10.11999/JEIT190314LIU Kun, WU Jianxin, ZHEN Jie, et al. Indoor localization algorithm based on array antenna and sparse Bayesian learning[J]. Journal of Electronics &Information Technology, 2020, 42(5): 1158–1164. doi: 10.11999/JEIT190314 [7] ACHUTEGUI K, MÍGUEZ J, RODAS J, et al. A multi-model sequential Monte Carlo methodology for indoor tracking: Algorithms and experimental results[J]. Signal Processing, 2012, 92(11): 2594–2613. doi: 10.1016/j.sigpro.2012.03.017 [8] KHALAJMEHRABADI A, GATSIS N, and AKOPIAN D. Modern WLAN fingerprinting indoor positioning methods and deployment challenges[J]. IEEE Communications Surveys & Tutorials, 2017, 19(3): 1974–2002. doi: 10.1109/COMST.2017.2671454 [9] CHEN Lina, LI Binghao, ZHAO Kai, et al. An improved algorithm to generate a Wi-Fi fingerprint database for indoor positioning[J]. Sensors, 2013, 13(8): 11085–11096. doi: 10.3390/s130811085 [10] HONKAVIRTA V, PERALA T, ALI-LOYTTY S, et al. A comparative survey of WLAN location fingerprinting methods[C]. The 6th Workshop on Positioning, Navigation and Communication, Hannover, Germany, 2009: 243–251. doi: 10.1109/WPNC.2009.4907834. [11] ZHANG Tianyu, ZHAO Qian, SHIN K, et al. Bayesian-optimization-based peak searching algorithm for clustering in wireless sensor networks[J]. Journal of Sensor and Actuator Networks, 2018, 7(1): 2. doi: 10.3390/jsan7010002 [12] ZHAO Yuxin, FRITSCHE C, YIN Feng, et al. Sequential Monte Carlo methods and theoretical bounds for proximity report based indoor positioning[J]. IEEE Transactions on Vehicular Technology, 2018, 67(6): 5372–5386. doi: 10.1109/TVT.2018.2799174 [13] ZHAO Yuxin, LIU Chao, MIHAYLOVA L S, et al. Gaussian processes for RSS fingerprints construction in indoor localization[C]. The 21st International Conference on Information Fusion, Cambridge, UK, 2018: 1377–1384. doi: 10.23919/ICIF.2018.8455842. [14] HE Suining, TAN Jiajie, and CHAN S H G. Towards area classification for large-scale fingerprint-based system[C]. 2016 ACM International Joint Conference on Pervasive and Ubiquitous Computing, Heidelberg, Germany, 2016: 232–243. doi: 10.1145/2971648.2971689. [15] 傅惠民, 杨海峰, 张勇波, 等. 基于空间特征分区和前点约束的WKNN室内定位方法[J]. 软件学报, 2019, 30(11): 3427–3439. doi: 10.13328/j.cnki.jos.005569FU Huimin, YANG Haifeng, ZHANG Yongbo, et al. WKNN indoor positioning algorithm based on spatial characteristics partition and former location restriction[J]. Journal of Software, 2019, 30(11): 3427–3439. doi: 10.13328/j.cnki.jos.005569 [16] LI Yan, WILLIAMS S, MORAN B, et al. High-dimensional probabilistic fingerprinting in wireless sensor networks based on a multivariate Gaussian mixture model[J]. Sensors, 2018, 18(8): 2602. doi: 10.3390/s18082602 [17] RAITOHARJU M, GARCÍA-FERNÁNDEZ Á F, HOSTETTLER R, et al. Gaussian mixture models for signal mapping and positioning[J]. Signal Processing, 2020, 168: 107330. doi: 10.1016/j.sigpro.2019.107330 [18] REYNOLDS D A, QUATIERI T F, and DUNN R B. Speaker verification using adapted Gaussian mixture models[J]. Digital Signal Processing, 2000, 10(1/3): 19–41. doi: 10.1006/dspr.1999.0361 -





 下载:
下载:



 下载:
下载:
