A Signal Acquisition Method Based on Multi-Sample Serial Fast Fourier Transform in High Dynamic and Low SNR Environment
-
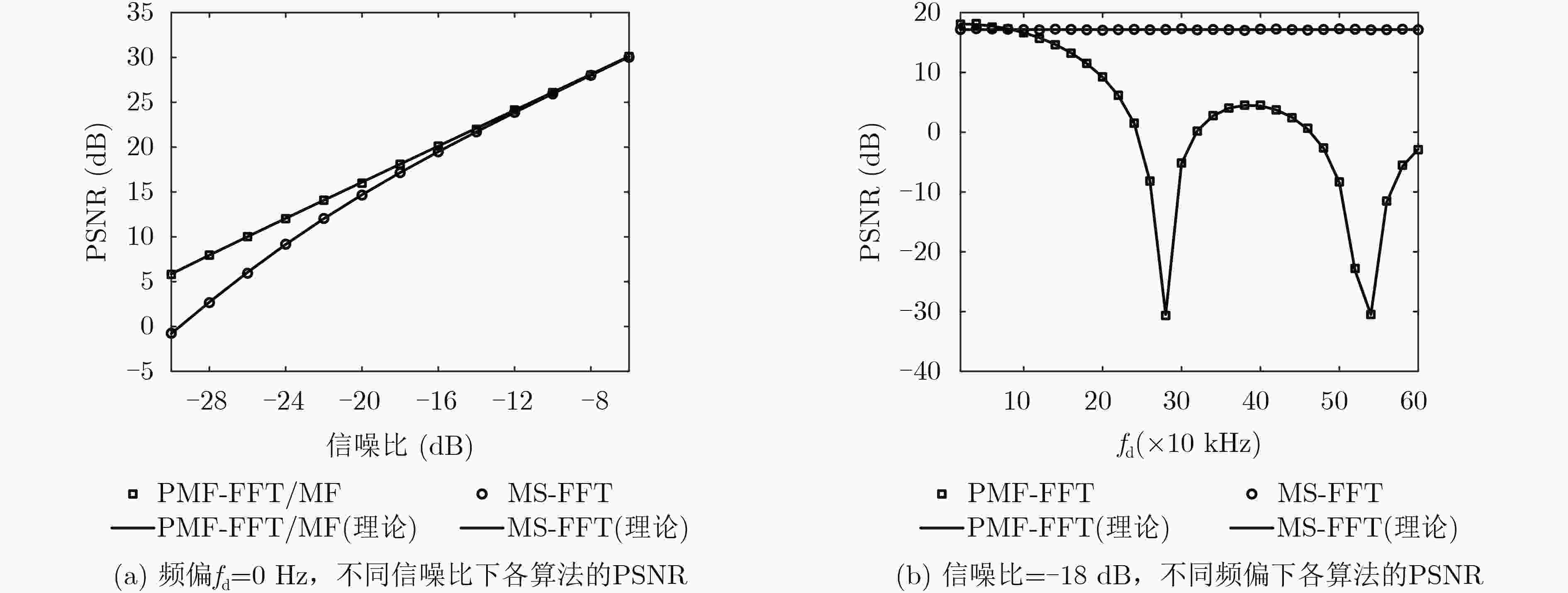
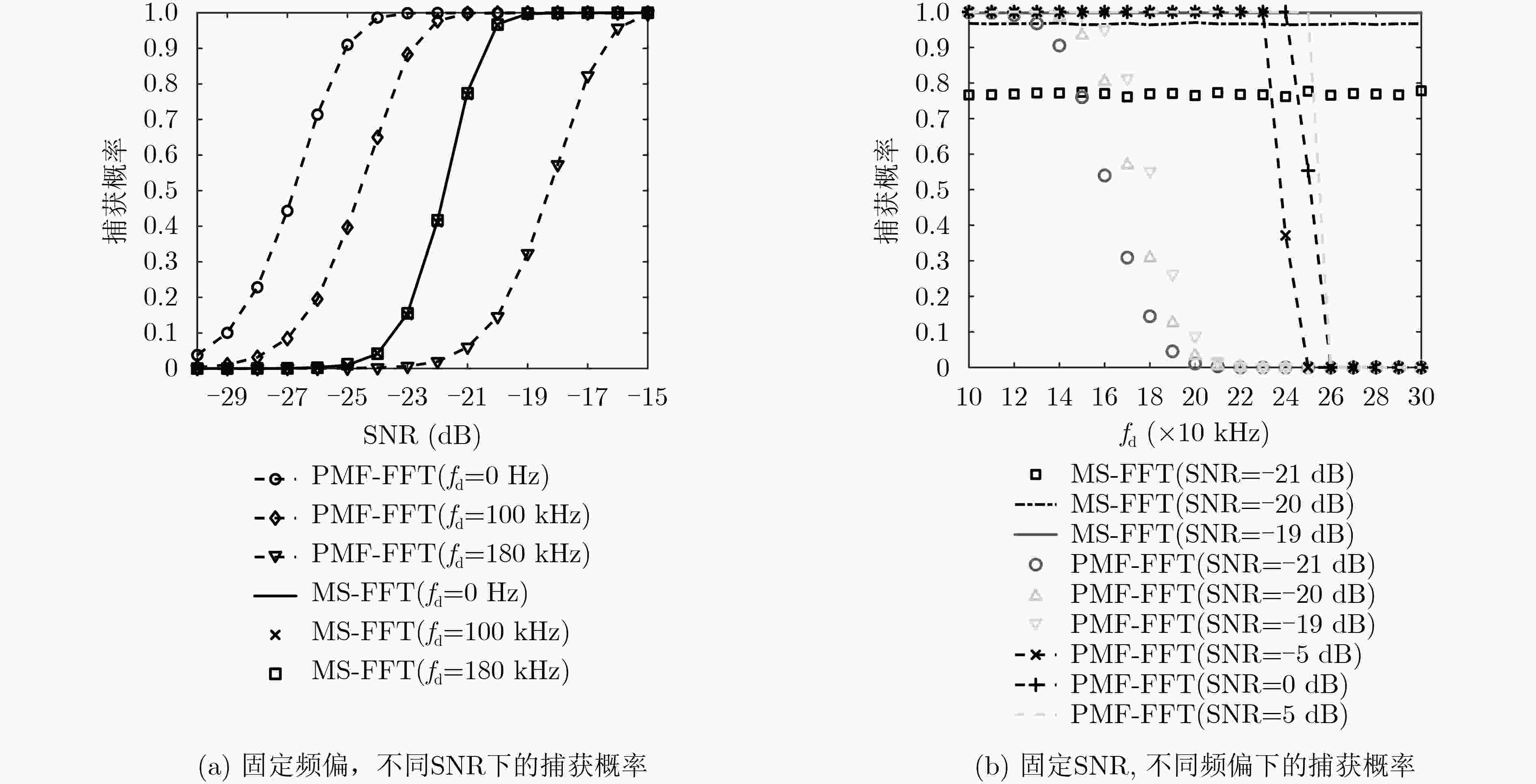
摘要: 高超音速技术是未来空间飞行器的发展趋势,同时对通信平台在超高动态、低信噪比环境下的快速捕获能力也提出了新的挑战。针对经典捕获算法受频偏影响的局限性,该文提出一种基于信号多样本点串行快速傅里叶变换的信号捕获算法(MS-FFT),所提算法通过串行执行多个样本点的FFT,采用非相干合并后的峰值搜索得到捕获结果,在不增加复杂度的条件下,避免了频偏对捕获性能的影响。通过对峰值信噪比(PSNR)理论公式的推导,证明了MS-FFT的频偏适应范围取决于采样率,随着数模转换器件采样能力的不断提升,具有比经典算法更大的频偏适应范围。最后,通过仿真验证了上述理论推导的正确性,证明了所提算法更加适合超高动态环境的应用场景。Abstract: Hypersonic technology is the development trend of space vehicles in the future. It also poses new challenges for the fast acquire capability of communication platforms in ultra-high dynamic and low signal-to-noise ratio environments. To overcome the limitation of the classic acquisition algorithm affected by frequency offset, a signal acquisition algorithm based on Multi-sample Serial Fast Fourier Transform (MS-FFT) is proposed. The proposed algorithm serially executes the FFT of multiple samples and runs the peak searching after non-coherent combining to obtain the acquire result. Without increasing the complexity, the influence of frequency offset on the acquisition performance is avoided. By deriving the theoretical formula of the Peak Signal-to-Noise Ratio (PSNR), it is proved that the frequency offset adaptation range of MS-FFT depends on the sampling rate and can be larger than the classical algorithm with the continuous improvement of the sampling capability of digital-analog conversion devices. Finally, the correctness of the above theoretical derivation is verified by simulation, and it is proved that the proposed algorithm is more suitable for the application scenarios of ultra-high dynamic environment.
-
表 1 MS-FFT算法流程表
输入:接收信号$y[n]$,本地参考序列$c$,同步头长度$N$,下采样率$d$,门限$T$,常数${\rm{C}}$ 输出:同步位置${n_s}$,频偏估计${f_{{\rm{est}}}}$ (1) (初始化设置):接收序列序号$n = - 1$,${P_n} = 0,y[n] = 0(n \le 0)$,设置${n_{\rm{A}}},{n_{\rm{B}}},{n_{\rm{C}}},{n_{\rm{S}}} = 0,{f_{{\rm{est}}}} = 0$; While ${n_{\rm{B}}} = = 0$ (2) 更新序号$n = n + 1$; (3) (更新接收序列):根据式(5)和式(6)得到并更新当前时刻$n$下的矩阵${{p}}$; (4) (FFT):计算矩阵${{p}}$最后一列的FFT,结果记为${{{P}}_n} = \{ {P_{j,{N_C} - 1}}\} _{j = 0}^{d - 1}$; (5) (非相干叠加):${z_n}(j) = \displaystyle\sum\nolimits_{i = n - d + 1}^n { { {\left| { {P_{ji} } } \right|}^2}\;,\;j = 0,1,···,N/d - 1}$; (6) (取最大值及下标):${\hat z_n} = \mathop {\max }\limits_{j = 0,1,···,N/d - 1} {z_n}(j)$,$k' = \mathop {\arg \max }\limits_{j = 0,1,···,N/d - 1} {z_n}(j)$; (7) (信号检测):若连续${{C} }$次检测$\{ {\hat { {z} }_n} > {\rm{T} }\& \& {\hat {{z} }_{n - { {C} } } } \le {T_{ {\rm{lb} } } }\}$为真,记${n_{\rm{A}}} = n$; 若$\{ {n_{\rm{A} } } \ne 0\& \& {\hat {\rm{z} }_n} \le T\}$为真,记${n_{\rm{B}}} = n$; end While
(8) (同步位置确定):${n_{\rm{C} } } = \mathop {\arg \max }\limits_{n = {n_{\rm{A} } } - {{C} } + 1,{n_{\rm{A} } } - {\rm{C} }, ··· ,{n_{\rm{B} } } } {\hat z_n}$, ${n_{\rm{S} } } = {n_{\rm{A} } } + {n_{\rm{C} } } - {{C} } + 1$;(9) (频偏估计):${{{{\overset{\frown}{{P}}} }}_{k'}} = {[{P_{{n_s} - d + 1,k'}},{P_{{n_s} - d + 2,k'}},···,{P_{{n_s},k'}}]^{\rm{T}}}$; ${ {{D} }_{k'} } = {\rm{diag} }(1,{{\rm{e}}^{ {\rm{j} }2\pi k'/N} },{{\rm{e}}^{ {\rm{j} }2\pi k' \cdot 2/N} }, ··· ,{{\rm{e}}^{j2\pi k' \cdot (d - 1)/N} })$; ${{P}}_{k'}^{(f)} = {\rm{FFT}}\{ {{{D}}_{k'}}{{{{\overset{\frown}{{P}}} }}_{k'}}\} = \{ {{P}}_{k'i}^{(f)}\} _{i = 0}^{d - 1}$;
$L = \mathop {\arg \max }\limits_{i = 0,1, ··· ,d - 1} {{P}}_{k'i}^{(f)}$;${f_{ {\rm{est} } } } = {f_{\rm{s}}}(k' + {N_{ {\rm{NC} } } }L)/N$。 -
[1] 申志强, 孟令杰. 临近空间高超声速飞行器测控通信的需求及策略分析[J]. 航天电子对抗, 2010, 26(2): 31–34. doi: 10.3969/j.issn.1673-2421.2010.02.009SHEN Zhiqiang and MENG Lingjie. Requirements and strategy analysis of TT& C used for ultrasonic speed aircraft[J]. Aerospace Electronic Warfare, 2010, 26(2): 31–34. doi: 10.3969/j.issn.1673-2421.2010.02.009 [2] 潘忠显. 高动态飞行器信号捕获算法研究[D]. [硕士论文], 西安电子科技大学, 2014: 29–30.PAN Zhongxian. A study on signals acquisition method of high dynamic vehicles[D]. [Master dissertation], Xidian University, 2014: 29–30. [3] KAY S M. Fundamentals of Statistical Signal Processing: Estimation Theory[M]. Upper Saddle River, NJ: Prentice Hall PTR, 1993: 157–168. [4] DIEZ J, PANTALEON C, VIELVA L, et al. A simple expression for the optimization of spread-spectrum code acquisition detectors operating in the presence of carrier-frequency offset[J]. IEEE Transactions on Communications, 2004, 52(4): 550–552. doi: 10.1109/TCOMM.2004.826345 [5] 祝武勇. 高动态下扩频通信系统同步技术研究及FPGA实现[D]. [硕士论文], 电子科技大学, 2019: 30–38.ZHU Wuyong. Research and FPGA implementation on synchronization technology of spread spectrum communication system under high dynamics[D]. [Master dissertation], University of Electronic Science and Technology of China, 2019: 30–38. [6] LIU Chang, ZHANG Jun, ZHU Yanbo, et al. Analysis and optimization of PMF-FFT acquisition algorithm for high-dynamic GPS signal[C]. 2011 IEEE 5th International Conference on Cybernetics and Intelligent Systems (CIS), Qingdao, China, 2011: 185–189. [7] 杨秦彪, 王祖林, 黄勤, 等. 高动态链路中折叠PMF-FFT快速捕获方法[J]. 系统工程与电子技术, 2016, 38(8): 1723–1729. doi: 10.3969/j.issn.1001-506X.2016.08.03YANG Qinbiao, WANG Zulin, HUANG Qin, et al. Folded PMF-FFT fast acquisition method for high dynamic scenarios[J]. Systems Engineering and Electronics, 2016, 38(8): 1723–1729. doi: 10.3969/j.issn.1001-506X.2016.08.03 [8] 王凯, 吴斌, 汪勃. 一种利用压缩感知改进的PMF-FFT扩频捕获算法[J]. 电讯技术, 2018, 58(6): 661–667. doi: 10.3969/j.issn.1001-893x.2018.06.008WANG Kai, WU Bin, WANG Bo. An improved PMF-FFT spread spectrum signal acquisition algorithm based on compressed sensing[J]. Telecommunication Engineering, 2018, 58(6): 661–667. doi: 10.3969/j.issn.1001-893x.2018.06.008 [9] LU Yongcai, ZONG Zhulin, and HE Chun. Low-resource and efficient parallel frequency search method for GNSS receiver[C]. 2010 International Conference on Computational Problem-Solving (ICCP), Lijiang, China, 2010: 136–140. [10] PAN Yi, ZHANG Tianqi, ZHANG Gang, et al. A novel acquisition algorithm based on PMF-apFFT for BOC modulated signals[J]. IEEE Access, 2019, 7: 46686–46694. doi: 10.1109/ACCESS.2019.2909787 [11] GUO Wenfei, NIU Xiaoji, GUO Chi, et al. A new FFT acquisition scheme based on partial matched filter in GNSS receivers for harsh environments[J]. Aerospace Science and Technology, 2017, 61: 66–72. doi: 10.1016/j.ast.2016.11.017 [12] 张天骐, 袁帅, 刘董华, 等. 高动态环境下高阶双二进制偏移载波信号的精确捕获[J]. 电子与信息学报, 2018, 40(11): 2728–2735. doi: 10.11999/JEIT180087ZHANG Tianqi, YUAN Shuai, LIU Donghua, et al. Accurate acquisition of high order double binary offset carrier signals for high dynamic environment[J]. Journal of Electronics &Information Technology, 2018, 40(11): 2728–2735. doi: 10.11999/JEIT180087 [13] LI Manshu, CHENG Yufan, WANG Xuezhe, et al. A synchronization acquisition algorithm for wireless communication system in high dynamic environment[C]. 2017 IEEE 17th International Conference on Communication Technology (ICCT), Chengdu, China, 2017: 1407–1411. [14] 曾芳玲, 欧阳晓凤, 徐浩, 等. 基于时频融合的长码直接捕获优化算法研究[J]. 电子与信息学报, 2019, 41(2): 309–316. doi: 10.11999/JEIT180119ZENG Fangling, OUYANG Xiaofeng, XU Hao, et al. Improved long-code direct acquisition algorithm based on time-frequency fusion[J]. Journal of Electronics &Information Technology, 2019, 41(2): 309–316. doi: 10.11999/JEIT180119 [15] SHI Lei, ZHU Congying, ZHAO Lei, et al. Fast Doppler shift acquisition method for hypersonic vehicle communications[J]. IET Communications, 2020, 14(3): 474–479. doi: 10.1049/iet-com.2018.6228 [16] STRÄSSLE C, MEGNET D, MATHIS H, et al. The Squaring-loss paradox[C]. ION GNSS 20th International Technical Meeting of the Satellite Division, Fort Worth, USA, 2007: 2715–2722. -





 下载:
下载:


 下载:
下载:
