Weighted Fusion Robust Incremental Kalman Filter
-
摘要: 在一定环境条件下,当系统的量测方程没有进行验证或校准时,使用该量测方程往往会产生未知的系统误差,从而导致较大的滤波误差。同样地,当系统的噪声方差不确定时,滤波的性能也将会变坏,甚至会引起滤波器发散。增量方程的引入可以有效消除系统的未知量测误差,从而带未知量测误差的欠观测系统的状态估计问题可以转换为增量系统的状态估计问题。该文考虑带未知量测误差和未知噪声方差的线性离散系统,首先提出一种基于增量方程的鲁棒增量Kalman滤波器。进而,基于线性最小方差最优融合准则,提出一种加权融合鲁棒增量Kalman滤波算法。仿真实例证明了所提算法的有效性和可行性。Abstract: Under certain environmental conditions, when the measurement equation of the system is not verified or calibrated, the use of the measurement equation will often produce unknown system errors, resulting in large filtering errors. Similarly, when the noise variance of the system is uncertain, the performance of the filter will deteriorate, and even cause the filter divergence. The introduction of incremental equation can effectively eliminate the unknown measurement error of the system, so that the state estimation of system under poor observation condition with unknown measurement error can be transformed into the state estimation of incremental system. In this paper, a robust incremental Kalman filter based on incremental equation is proposed for linear discrete systems with unknown measurement error and unknown noise variance. Then, based on the linear minimum variance optimal fusion criterion, a weighted fusion robust incremental Kalman filtering algorithm is proposed. Simulation results show the effectiveness and feasibility of the proposed algorithm.
-
表 1 局部和加权融合鲁棒增量Kalman滤波器在时刻k=200时的均方误差值比较
传感器1 传感器2 传感器3 融合器 0.2593 0.2610 0.2597 0.2490 -
[1] KALMAN R E. A new approach to linear filtering and prediction problems[J]. Journal of Fluids Engineering, 1960, 82(1): 35–45. doi: 10.1115/1.3662552 [2] 邓自立, 齐文娟, 张鹏. 鲁棒整合卡尔曼滤波理论及应用[M]. 哈尔滨: 哈尔滨工业大学出版社, 2016: 4.DENG Zili, QI Wenjuan, and ZHANG Peng. Robust Fusion Kalman Filtering Theory with Applications[M]. Harbin: Harbin Institute of Technology Press, 2016: 4. [3] 杨峰, 郑丽涛, 王家琦, 等. 双层无迹卡尔曼滤波[J]. 自动化学报, 2019, 45(7): 1386–1391. doi: 10.16383/j.aas.c180349YANG Feng, ZHENG Litao, WANG Jiaqi, et al. Double layer unscented Kalman filter[J]. Acta Automatica Sinica, 2019, 45(7): 1386–1391. doi: 10.16383/j.aas.c180349 [4] 张宏伟, 谢维信. 平滑约束无迹卡尔曼滤波器[J]. 信号处理, 2019, 35(3): 466–471. doi: 10.16798/j.issn.1003-0530.2019.03.019ZHANG Hongwei and XIE Weixin. Smoothly constrained unscented Kalman filter[J]. Journal of Signal Processing, 2019, 35(3): 466–471. doi: 10.16798/j.issn.1003-0530.2019.03.019 [5] 耿友林, 解成博, 尹川, 等. 基于卡尔曼滤波的接收信号强度指示差值定位算法[J]. 电子与信息学报, 2019, 41(2): 455–461. doi: 10.11999/JEIT180268GENG Youlin, XIE Chengbo, YI Chuan, et al. Received signal strength indication difference location algorithm based on Kalman filter[J]. Journal of Electronics &Information Technology, 2019, 41(2): 455–461. doi: 10.11999/JEIT180268 [6] 王少帅, 李登峰. 基于无迹卡尔曼滤波的路面附着系数估计[J]. 电子设计工程, 2020, 28(1): 27–31. doi: 10.14022/j.issn1674-6236.2020.01.007WANG Shaoshuai and LI Dengfeng. Road adhesion coefficient estimation based on unscented Kalman filter[J]. Electronic Design Engineering, 2020, 28(1): 27–31. doi: 10.14022/j.issn1674-6236.2020.01.007 [7] 沈连丰, 张瑞, 朱亚萍, 等. 面向自动驾驶的车辆精确实时定位算法[J]. 电子与信息学报, 2020, 42(1): 28–35. doi: 10.11999/JEIT190610SHEN Lianfeng, ZHANG Rui, ZHU Yaping, et al. High-precision and real-time localization algorithm for automatic driving vehicles[J]. Journal of Electronics &Information Technology, 2020, 42(1): 28–35. doi: 10.11999/JEIT190610 [8] SUN Xiaojun, GAO Yuan, DENG Zili, et al. Multi-model information fusion Kalman filtering and white noise deconvolution[J]. Information Fusion, 2010, 11(2): 163–173. doi: 10.1016/j.inffus.2009.06.004 [9] 刘利生, 吴斌, 杨萍. 航天器精确定轨与自校准技术[M]. 北京: 国防工业出版社, 2005: 9.LIU Lisheng, WU Bin, and YANG Ping. Orbit Precision Determination & Self-Calibration Technique of Spacecraft[M]. Beijing: National Defense Industry Press, 2005: 9. [10] 傅惠民, 娄泰山, 吴云章. 欠观测条件下的扩展增量Kalman滤波方法[J]. 航空动力学报, 2012, 27(4): 777–781. doi: 10.13224/j.cnki.jasp.2012.04.004FU Huimin, LOU Taishan, and WU Yunzhang. Extended incremental Kalman filter method under poor observation condition[J]. Journal of Aerospace Power, 2012, 27(4): 777–781. doi: 10.13224/j.cnki.jasp.2012.04.004 [11] 傅惠民, 娄泰山, 吴云章. 增量粒子滤波方法[J]. 航空动力学报, 2013, 28(6): 1201–1207. doi: 10.13224/j.cnki.jasp.2013.06.005FU Huimin, LOU Taishan, and WU Yunzhang. Incremental particle filter method[J]. Journal of Aerospace Power, 2013, 28(6): 1201–1207. doi: 10.13224/j.cnki.jasp.2013.06.005 [12] 傅惠民, 吴云章, 娄泰山. 欠观测条件下的增量Kalman滤波方法[J]. 机械强度, 2012, 34(1): 43–47. doi: 10.16579/j.issn.1001.9669.2012.01.014FU Huimin, WU Yunzhang, and LOU Taishan. Incremental Kalman filter method under poor observation condition[J]. Journal of Mechanical Strength, 2012, 34(1): 43–47. doi: 10.16579/j.issn.1001.9669.2012.01.014 [13] 孙小君, 周晗, 闫广明. 基于新息的自适应增量Kalman滤波器[J]. 电子与信息学报, 2020, 42(9): 2223–2230. doi: 10.11999/JEIT190493SUN Xiaojun, ZHOU Han, and YAN Guangming. Adaptive incremental Kalman filter based on innovation[J]. Journal of Electronics &Information Technology, 2020, 42(9): 2223–2230. doi: 10.11999/JEIT190493 [14] SUN Xiaojun and YAN Guangming. Multi-sensor optimal weighted fusion incremental Kalman smoother[J]. Journal of Systems Engineering and Electronics, 2018, 29(2): 262–268. doi: 10.21629/JSEE.2018.02.06 [15] 蔡博, 高宏力, 宋兴国, 等. 基于改进增量卡尔曼滤波算法的UWB室内定位研究[J]. 机械设计与制造, 2020(2): 22–25. doi: 10.3969/j.issn.1001-3997.2020.02.006CAI Bo, GAO Hongli, SONG Xingguo, et al. Research of UWB indoor location based on improved incremental Kalman filter algorithm[J]. Machinery Design &Manufacture, 2020(2): 22–25. doi: 10.3969/j.issn.1001-3997.2020.02.006 [16] 伍锡锈. 基于增量Kalman滤波的GPS多路径效应系统误差研究[J]. 测绘工程, 2012, 21(6): 35–37. doi: 10.3969/j.issn.1006-7949.2012.06.009WU Xixiu. GPS multipath effect systematic error research based on incremental Kalman filter[J]. Engineering of Surveying and Mapping, 2012, 21(6): 35–37. doi: 10.3969/j.issn.1006-7949.2012.06.009 [17] 肖曦, 王伟华, 吕志鹏. 一种基于增量式卡尔曼滤波器的PMSM转速滤波算法[J]. 电机与控制学报, 2014, 18(10): 104–111. doi: 10.3969/j.issn.1007-449X.2014.10.016XIAO Xi, WANG Weihua, and LÜ Zhipeng. Filtering algorithm of speed for PMSM based on incremental Kalman filter[J]. Electric Machines and Control, 2014, 18(10): 104–111. doi: 10.3969/j.issn.1007-449X.2014.10.016 [18] LEWIS F L, XIE Lihua, and POPA Dan. Optimal and Robust Estimation[M]. 2nd ed. Boca Raton: CRC Press, 2008. [19] QU Xiaomei and ZHOU Jie. The optimal robust finite-horizon Kalman filtering for multiple sensors with different stochastic failure rates[J]. Applied Mathematics Letters, 2013, 26(1): 80–86. doi: 10.1016/j.aml.2012.03.036 [20] ZHU Xing, SOH Y C, and XIE Lihua. Design and analysis of discrete-time robust Kalman filters[J]. Automatica, 2002, 38(6): 1069–1077. doi: 10.1016/S0005-1098(01)00298-9 [21] XI Hongsheng. The guaranteed estimation performance filter for discrete-time descriptor systems with uncertain noise[J]. International Journal of Systems Science, 1997, 28(1): 113–121. doi: 10.1080/00207729708929368 [22] ZHAO Dong, DING S X, KARIMI H R, et al. On robust Kalman filter for two-dimensional uncertain linear discrete time-varying systems: A least squares method[J]. Automatica, 2019, 99: 203–212. doi: 10.1016/j.automatica.2018.10.029 [23] DONG Zhe and YOU Zheng. Finite-horizon robust Kalman filtering for uncertain discrete time-varying systems with uncertain-covariance white noises[J]. IEEE Signal Processing Letters, 2006, 13(8): 493–496. doi: 10.1109/LSP.2006.873148 [24] 傅惠民, 吴琼. 线性独立增量过程分析方法[J]. 航空动力学报, 2010, 25(4): 930–935.FU Huimin and WU Qiong. Analysis method for linear process with independent increments[J]. Journal of Aerospace Power, 2010, 25(4): 930–935. -





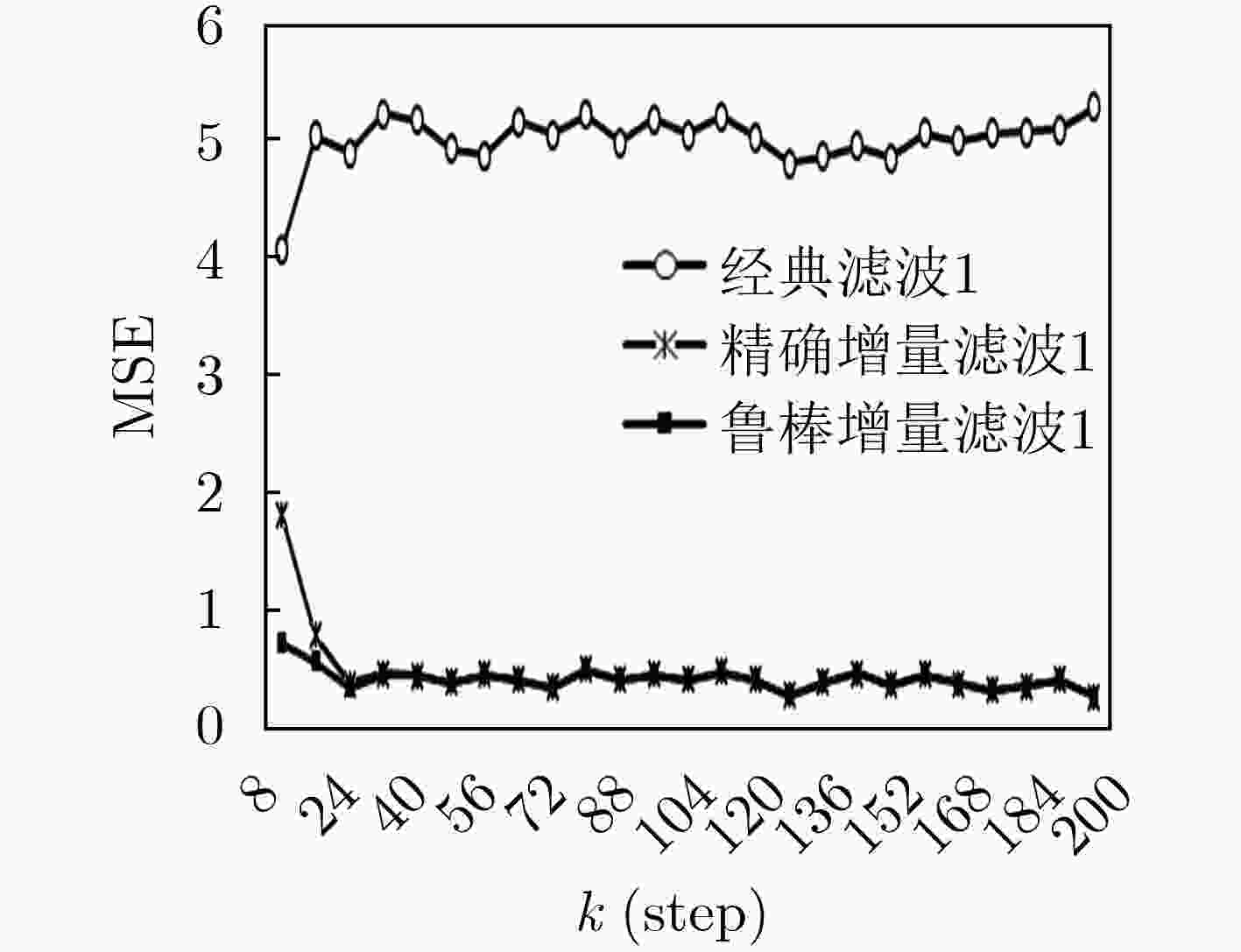
 下载:
下载:
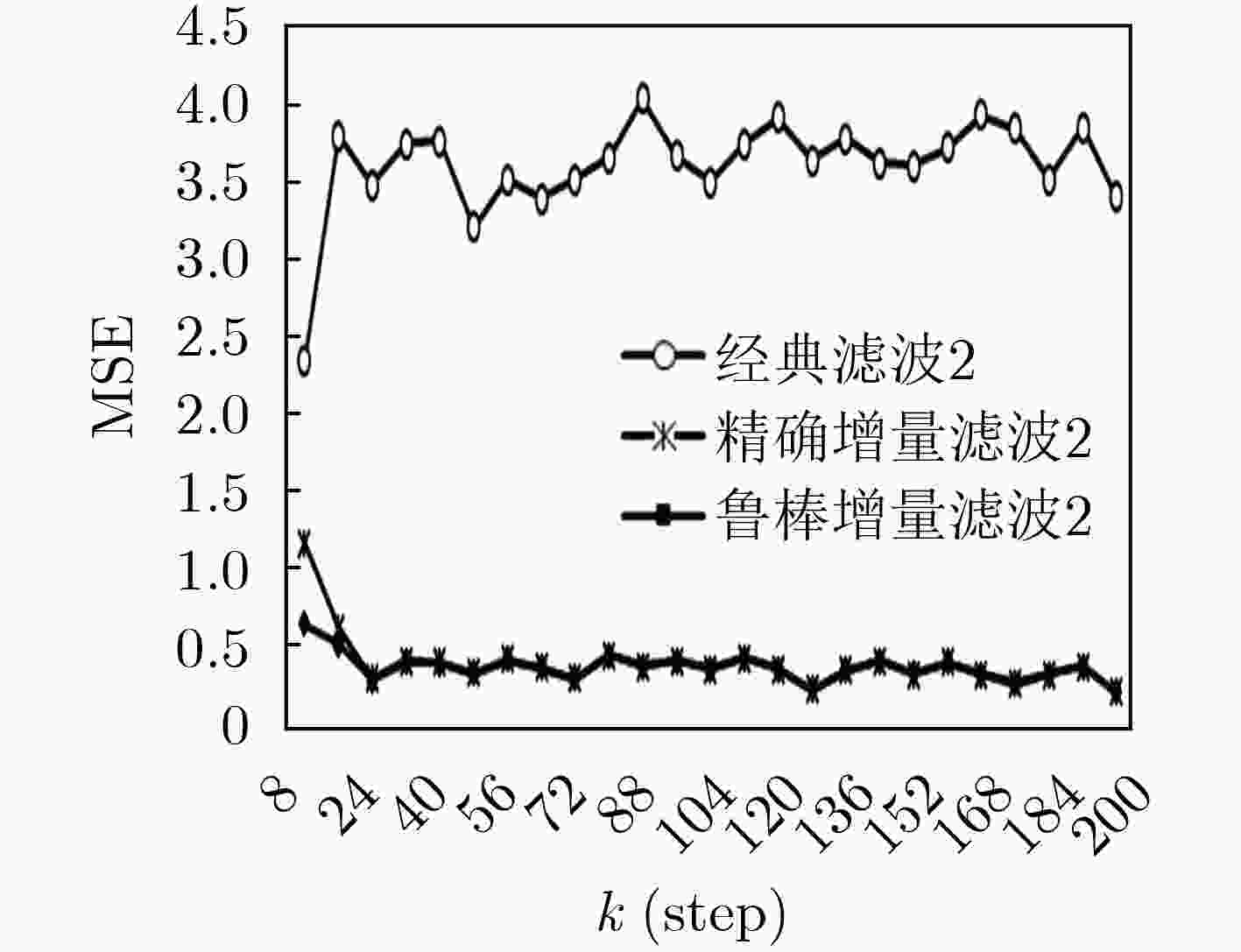
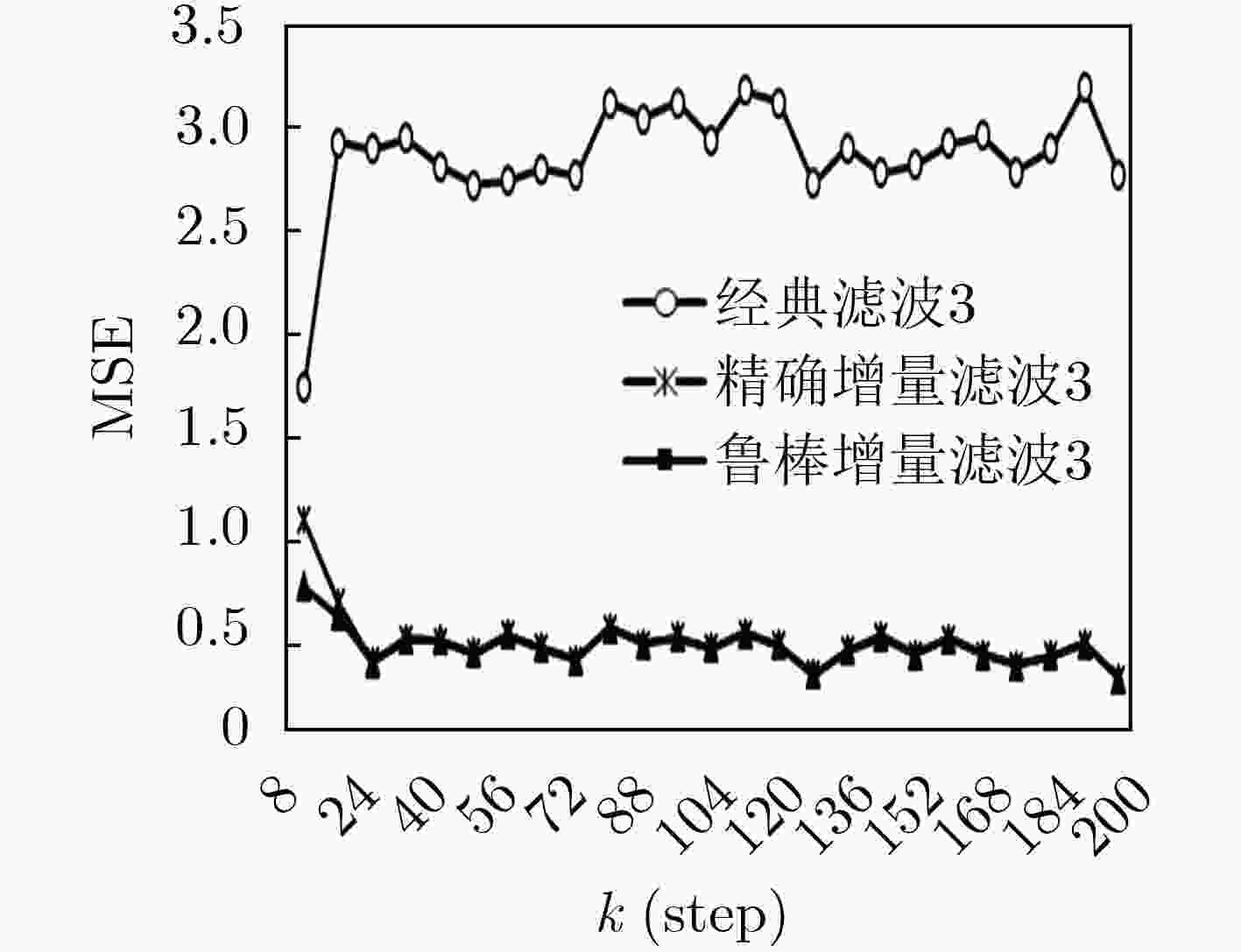
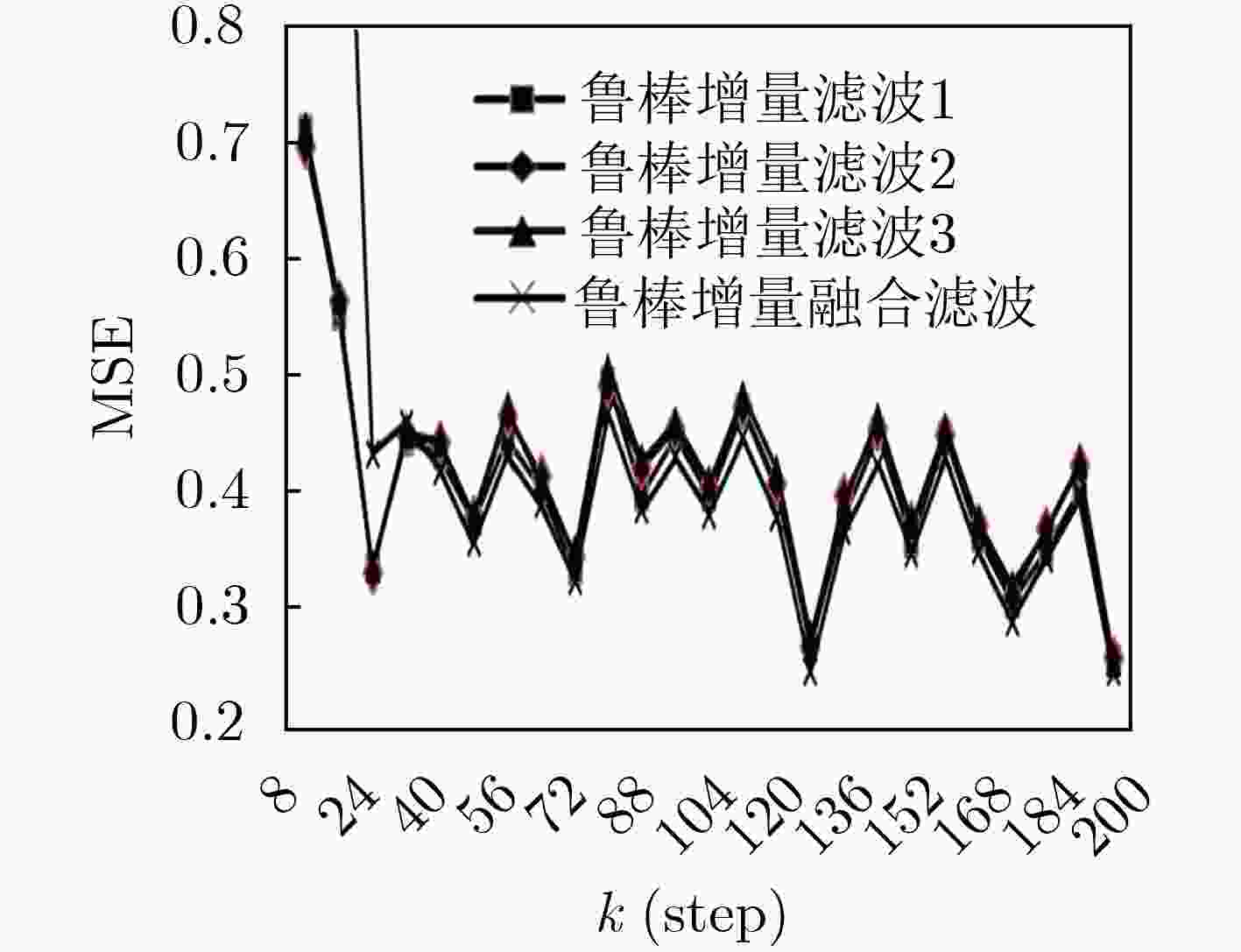


 下载:
下载:
