二进制指数退避的Gossip算法研究

成卫青; 张蕾

doi:10.11999/JEIT200094

二进制指数退避的Gossip算法研究

doi: 10.11999/JEIT200094

成卫青^{1, 2, ,},
张蕾¹

1.
南京邮电大学计算机学院南京 210023
2.
东南大学计算机网络和信息集成教育部重点实验室南京 211189

基金项目: 国家自然科学基金(61170322)，江苏省研究生教育教学改革课题(JGZZ19_038)

详细信息

作者简介:
成卫青：女，1972年生，教授，研究方向为网络测量、分布式系统和模式识别

张蕾：女，1994年生，硕士，研究方向为分布式系统

通讯作者:
成卫青　chengweiq@njupt.edu.cn

中图分类号: TP391; TP393
计量
- 文章访问数: 921
- HTML全文浏览量: 612
- PDF下载量: 46
- 被引次数: 0
出版历程
- 收稿日期: 2020-02-11
- 修回日期: 2021-03-23
- 网络出版日期: 2021-06-03
- 刊出日期: 2021-12-21

Research on Gossip Algorithms with Binary Exponential Backoff

Weiqing CHENG^{1, 2
, ,},
Lei ZHANG¹

1.
School of Computer, Nanjing University of Posts and Telecommunications, Nanjing 210023, China
2.
Key Laboratory of Computer Network and Information Integration (Ministry of Education), Southeast University, Nanjing 211189, China

摘要

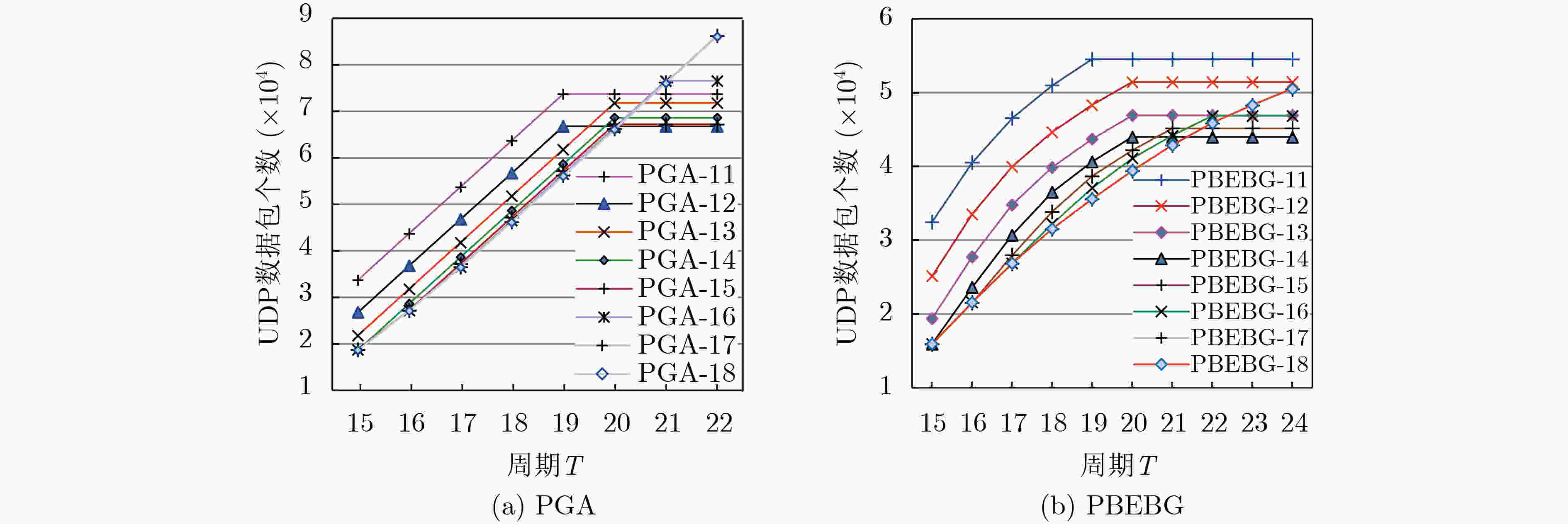
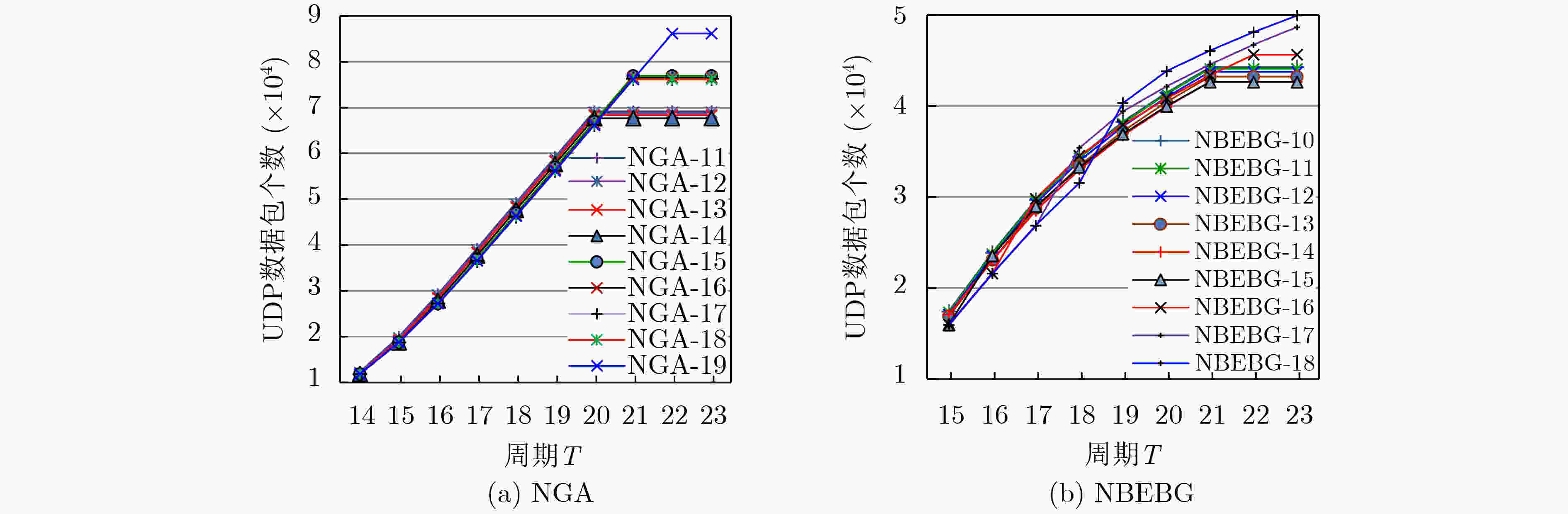
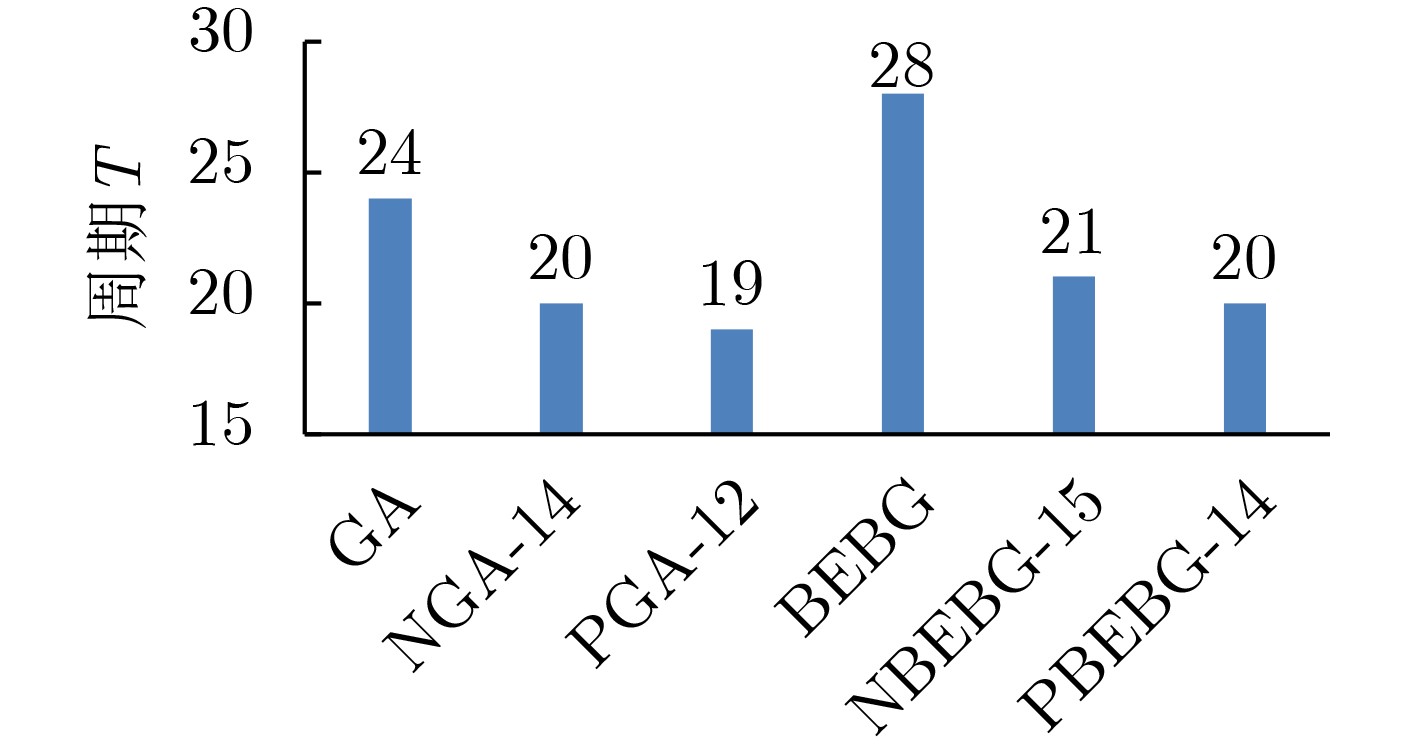
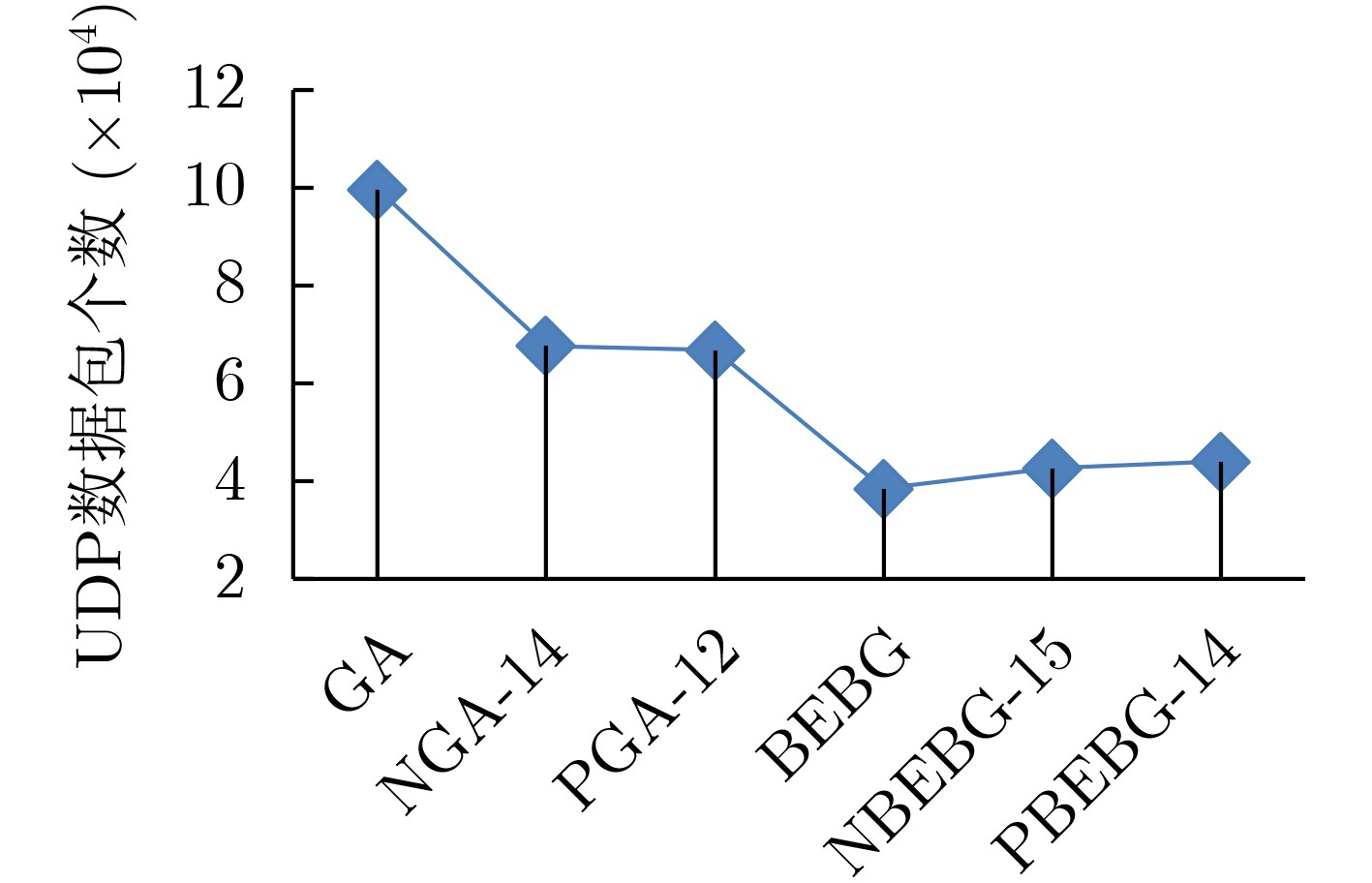
摘要: 为减少Gossip算法进行信息传播的通信开销，该文提出一个将二进制指数退避算法与经典Gossip算法相结合的二进制指数退避的Gossip算法(BEBG)，其信息传播策略是一个节点收到同一信息的次数越多，继续传播该信息的概率就越低。理论分析与仿真实验表明，BEBG能够有效减少信息传播冗余，网络中有10⁴个节点时比经典Gossip算法减少了约61%网络负载。为解决BEBG存在的边缘节点问题，进一步提出了两个BEBG改进算法，引入Pull的PBEBG和引入向邻居节点Push的NBEBG。实验结果表明，两个算法能够消除边缘节点，当网络中有10⁴个节点时，它们与相应的分别引入相同Pull和Push的经典Gossip算法相比，分别减少了约34%和37%的网络负载。
- 分布式系统 /
- 信息传播 /
- Gossip算法
Abstract: In order to reduce the communication cost of classic Gossip algorithm for information dissemination, an improved Gossip algorithm BEBG (Gossip with Binary Exponential Backoff) is proposed, which combines the binary exponential backoff algorithm with Gossip algorithm. Its information dissemination strategy is that the more times that a node has received the same information, the lower probability it continues to spread the information. Theoretical analysis and simulation results show that the BEBG can effectively reduce the redundancy of information propagation, and compared with the classic Gossip algorithm, the network load is reduced by about 61% when there are 10⁴ nodes in the network. In order to solve the problem of edge nodes in the BEBG, two improved BEBG algorithms PBEBG that introduces Pull operations and NBEBG that introduces pushing information to a Neighbor node are further proposed. Experimental results show that the two algorithms can eliminate the edge nodes, and when there are 10⁴ nodes in the network, they reduce the network load by about 34% and 37% respectively compared with the corresponding improved classic Gossip algorithms which introduce the same pull and push respectively.
- Distributed systems /
- Information dissemination /
- Gossip algorithm

HTML全文

图 1 PBEBG算法中的“拉”

下载: 全尺寸图片幻灯片

图 2 NBEBG中向前1个邻居节点推送信息

下载: 全尺寸图片幻灯片

图 3 6种算法名称

下载: 全尺寸图片幻灯片

图 4 不同“Pull”值时，算法PGA和PBEBG随时间变化的总信息量

下载: 全尺寸图片幻灯片

图 5 不同“Push”值时，算法NGA和NBEBG随时间变化的总信息量

下载: 全尺寸图片幻灯片

图 6 6种算法将信息传遍整个网络所需周期对比

下载: 全尺寸图片幻灯片

图 7 6种算法总信息量对比

下载: 全尺寸图片幻灯片

表 1 BEBG算法的信息发送过程(算法1)

Data: 节点集合 V，本节点 v 向外传播信息的概率 p；
Result: 如果本节点 v 已着色，它可能发送待传播更新信息 info 　　　　给另一个节点。
(1) 初始化
(2) if 本节点 v 已着色(已获得 info) then
(3)　　　根据传播概率 p 决定是否传播 info
(4)　　　 if 本节点决定发送 then
(5)　　　　从 V-{v} 中随机选择一个节点
(6)　　　　向该节点发送 info
(7)　　　 end if
(8) end if

下载: 导出CSV

表 2 BEBG算法的信息接收过程(算法2)

Input: 本轮中可能接收到所关注的信息 info；
Result: 如果本轮中收到了所关注的信息 info，则本节点的传播　　　　概率 p 可能被改变，且本节点为已着色。
(1) first ← false
(2) reflag ← true, changP ← false
(3) while reflag do
(4)　　　执行接收操作
(5)　　　if 如果接收操作没有超时 then
(6)　　　　　　接收消息
(7)　　　　　　if 消息包含关注的信息 info then
(8)　　　　　　　　changeP ← true
(9)　　　　　　　　if 本节点未着色 then
(10)　　　　　　　　　　p ← 1
(11)　　　　　　　　　　first ← true
(12)　　　　　　　　　　colored ← true
(13)　　　　　　　　end if
(14)　　　　　　end if
(15)　　 else
(16)　　　　　　if first then
(17)　　　　　　　　changeP←false
(18)　　　　　　　　first ←false
(19)　　　　　　end if
(20)　　　　　　if changeP and p > 1/32 then
(21)　　　　　　　　p ← p/2
(22)　　　　　　end if
(23)　　　　　　reflag ← false
(24)　　　　end if
(25) end while

下载: 导出CSV

表 3 PBEBG算法的发送过程(算法3)

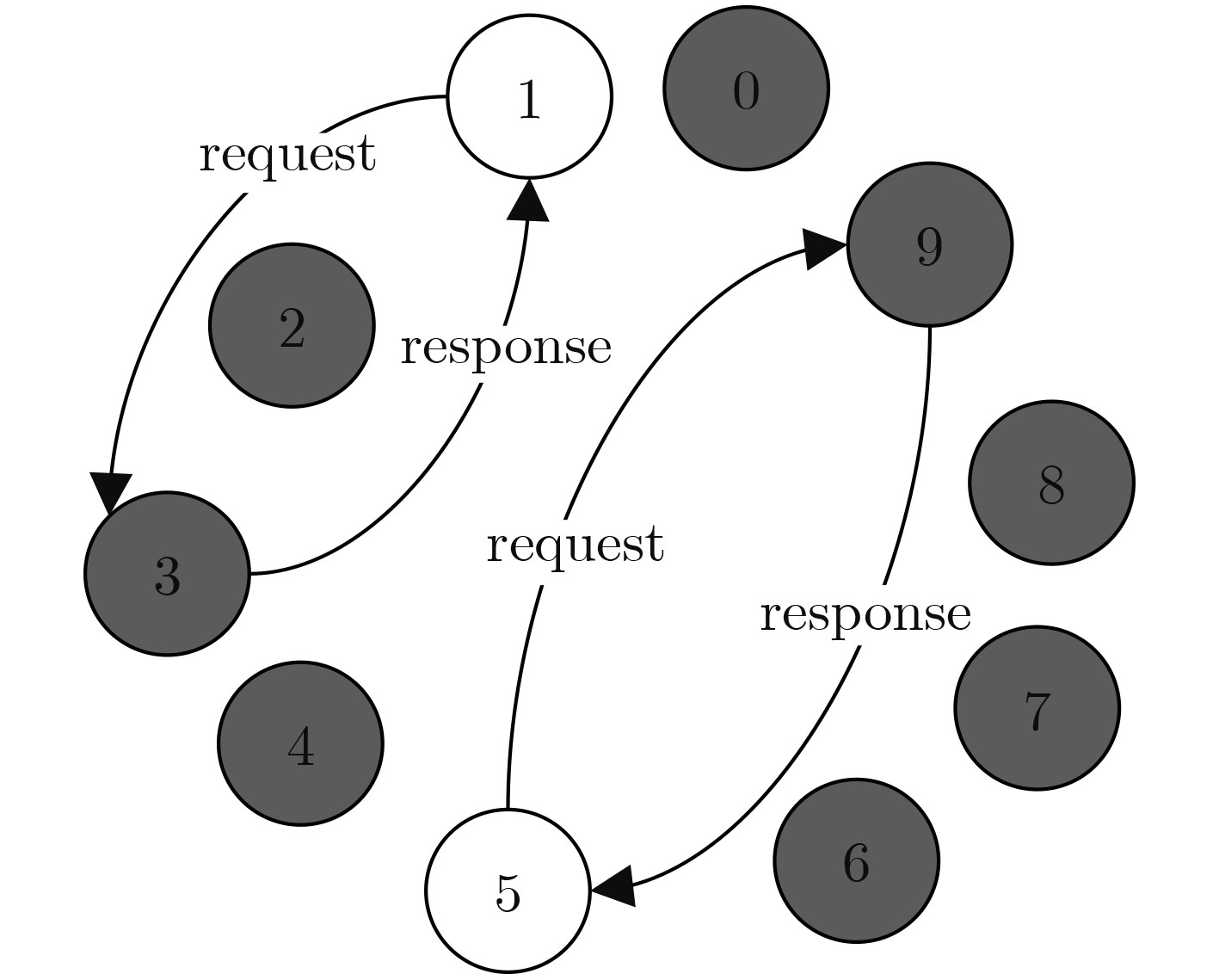
Data: 节点集合 V，当前轮次 T，本节点传播概率 p，响应标记response，请求标记 request ，最后一个发来请求的节点 s；
Result: 如果本节点 v 未着色且 request 为真，则发送请求给另一个节点；如果本节点已着色，可能发送待传播信息info给另一个节点；或者如果response为真则发送info给最后一个发来请求的节点 s。
(1) 初始化
(2) if 本节点 v 未着色且决定pull (即request为真) then
(3)　　　从 V-{v} 中随机选择一个节点
(4)　　　向该节点发送一个请求
(5) end if
(6) if 本节点 v 已着色(已获得 info)then
(7)　　　 if 本节点在上一轮收到了请求(即response为真) then
(8)　　　　　向最后一个发来请求的节点 s 发送info
(9)　　　 else
(10)　　　　　根据传播概率 p 决定是否传播 info
(11)　　　　　 if 本节点决定发送 then
(12)　　　　　　　　从 V-{v} 中随机选择一个节点
(13)　　　　　　　　向该节点发送 info
(14)　　　　　 end if
(15)　　　 end if
(16) end if

下载: 导出CSV

表 4 PBEBG算法的接收过程(算法4)

Data: 节点集合 V，当前轮次 T，阈值 Pull；
Input: 本轮中可能接收到所关注的信息 info 和请求；
Result: 如果本轮中收到了所关注的信息 info，则本节点的传播概率 p 可能被改变，且本节点为已着色；如果本轮中收到了请求，则设置响应标记 response 为真，并记录最后一个发来请求的节点 s；如果本节点在本轮最终仍是未着色的，且当前轮次T>=Pull，则设置请求标记 request 为真。
(1) first ← false, response ← false, request ← false
(2) reflag ← true, changP ← false
(3) while reflag do
(4) 　　　执行接收操作
(5) 　　　if 如果接收操作没有超时 then
(6) 　　　　　　接收来自节点src的消息
(7) 　　　　　　if 这是一个请求消息 then
(8) 　　　　　　　　 response ← true, s ← src
(9) 　　　　　　else if 消息包含关注的信息 then
(10) 　　　　　　　　changeP ← true
(11) 　　　　　　　　request ← false
(12) 　　　　　　　　if 本节点未着色 then
(13) 　　　　　　　　　　p ← 1
(14) 　　　　　　　　　　first ← true
(15) 　　　　　　　　　　colored ← true
(16) 　　　　　　　　end if
(17) 　　　　　　end if
(18) 　　　else
(19) 　　　　　　if 本节点未着色且 T>=Pull then
(20) 　　　　　　　　request←true
(21) 　　　　　　end if
(22) 　　　　　　if first then
(23) 　　　　　　　　changeP←false
(24) 　　　　　　　　first←false
(25) 　　　　　　end if
(26) 　　　　　　if changeP and p > 1/32 then
(27) 　　　　　　　　p ← p/2
(28) 　　　　　　end if
(29) 　　　　　　reflag ← false
(30) 　　　end if
(31) end while

下载: 导出CSV

表 5 NBEBG算法的信息发送过程(算法5)

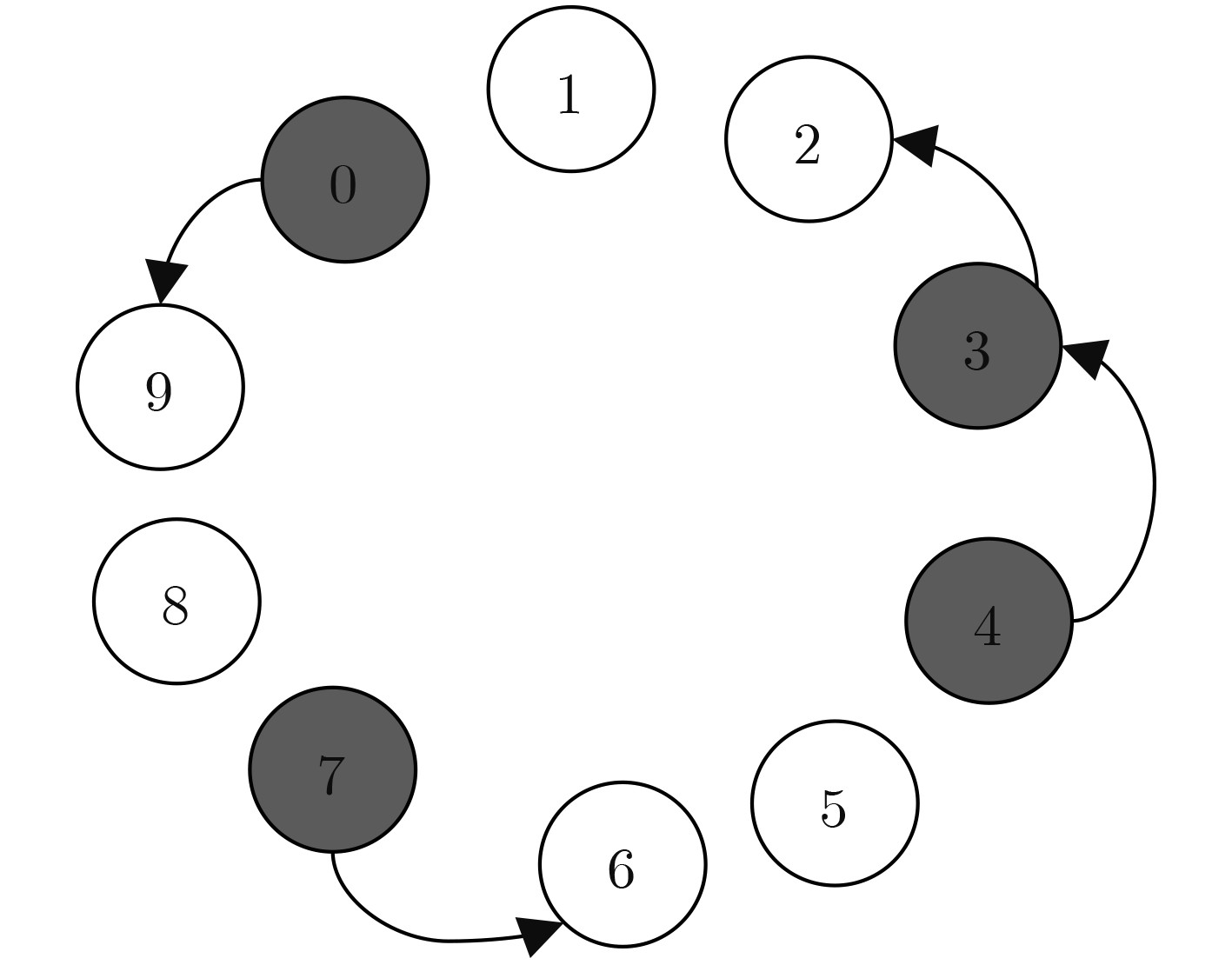
Data: 节点集合 V，当前轮次 T，本节点 v 向外传播信息的概率 p，标记 hasPush，阈值Push；
Result: 如果本节点 v 已着色，它可能发送待传播更新信息 info 给另一个节点，或者如果 hasPush 为假且 T>=Push 则发送 info 给本节点的前一个节点。
(1) 初始化
(2) if 本节点 v 已着色(已获得 info) then
(3)　　 if!hasPush and T>=Push then
(4)　　　　发送 info 给本节点的前一个节点
(5)　　　　 hasPush ←true
(6)　　 else
(7)　　　　根据传播概率 p 决定是否传播 info
(8)　　　　 if 本节点决定发送 then
(9)　　　　　　　从 V-{v} 中随机选择一个节点
(10)　　　　　　　向该节点发送 info
(11)　　　　end if
(12)　　 end if
(13) end if

下载: 导出CSV

参考文献(23)

[1]	DEMERS A, GREENE D, HOUSER C, et al. Epidemic algorithms for replicated database maintenance[J]. ACM SIGOPS Operating Systems Review, 1988, 22(1): 8–32. doi: 10.1145/43921.43922
[2]	GUPTA I, VAN RENESSE R, and BIRMAN K P. Scalable fault-tolerant aggregation in large process groups[C]. 2001 International Conference on Dependable Systems and Networks, Gothenburg, Sweden, 2001: 433–442. doi: 10.1109/DSN.2001.941427.
[3]	JELASITY M and BABAOGLU O. T-Man: Gossip-based overlay topology management[C]. The 3rd International Workshop on Engineering Self-Organising Applications, Utrecht, The Netherlands, 2005: 1–15. doi: 10.1007/11734697_1.
[4]	PROVENSI L L, SINGH A, ELIASSEN F, et al. Maelstream: Self-organizing media streaming for many-to-many interaction[J]. IEEE Transactions on Parallel and Distributed Systems, 2018, 29(6): 1342–1356. doi: 10.1109/TPDS.2018.2791599
[5]	LIU Mengdi, XU Guangquan, ZHANG Jun, et al. Roundtable gossip algorithm: A novel sparse trust mining method for large-scale recommendation systems[C]. The 18th International Conference on Algorithms and Architectures for Parallel Processing, ICA3PP 2018, Guangzhou, China, 2018: 495–510. doi: 10.1007/978-3-030-05063-4_37.
[6]	LAVINIA A, DOBRE C, POP F, et al. A failure detection system for large scale distributed systems[J]. International Journal of Distributed Systems and Technologies, 2011, 2(3): 64–87. doi: 10.1109/CISIS.2010.29
[7]	VAN RENESSE R, BIRMAN K P, and VOGELS W. Astrolabe: A robust and scalable technology for distributed system monitoring, management, and data mining[J]. ACM Transactions on Computer Systems, 2003, 21(2): 164–206. doi: 10.1145/762483.762485
[8]	PIETRO R D and MICHIARDI P. Gossip-based aggregate computation: Computing faster with non address-oblivious schemes[C]. The 27th ACM Symposium on Principles of Distributed Computing, Toronto, Canada, 2008: 442. doi: 10.1145/1400751.1400837.
[9]	WANG Gang, WANG Zhiyue, and WU Jie. A local average broadcast gossip algorithm for fast global consensus over graphs[J]. Journal of Parallel and Distributed Computing, 2017, 109: 301–309. doi: 10.1016/j.jpdc.2017.05.008
[10]	张仕将, 柴晶, 陈泽华, 等. 基于Gossip协议的拜占庭共识算法[J]. 计算机科学, 2018, 45(2): 20–24. doi: 10.11896/j.issn.1002-137X.2018.02.004 ZHANG Shijiang, CHAI Jing, CHEN Zehua, et al. Byzantine consensus algorithm based on gossip protocol[J]. Computer Science, 2018, 45(2): 20–24. doi: 10.11896/j.issn.1002-137X.2018.02.004
[11]	WANG Huiwei, LIAO Xiaofeng, WANG Zidong, et al. Distributed parameter estimation in unreliable sensor networks via broadcast gossip algorithms[J]. Neural Networks, 2016, 73: 1–9. doi: 10.1016/j.neunet.2015.09.008
[12]	AZIMI R and SAJEDI H. Peer sampling gossip-based distributed clustering algorithm for unstructured P2P networks[J]. Neural Computing and Applications, 2018, 29(2): 593–612. doi: 10.1007/s00521-017-3119-0
[13]	AZIMI R and SAJEDI H. A decentralized gossip based approach for data clustering in peer-to-peer networks[J]. Journal of Parallel and Distributed Computing, 2018, 119: 64–80. doi: 10.1016/j.jpdc.2018.03.009
[14]	FEMMINELLA M, FRANCESCANGELI R, REALI G, et al. Gossip-based signaling dissemination extension for next steps in signaling[C]. 2012 IEEE Network Operations and Management Symposium, Maui, United States, 2012: 1022–1028. doi: 10.1109/NOMS.2012.6212024.
[15]	崔闻. 基于Gossip的无线传感器网络定位算法研究[D]. [硕士论文], 哈尔滨工业大学, 2014. CUI Wen. Research on gossip-based localization algorithms in wireless sensor networks[D]. [Master dissertation], Harbin Institute of Technology, 2014.
[16]	LIU Yan, NIU Di, and KHABBAZIAN M. Cooper: Expedite batch data dissemination in computer clusters with coded gossips[J]. IEEE Transactions on Parallel and Distributed Systems, 2017, 28(8): 2204–2217. doi: 10.1109/TPDS.2017.2654242
[17]	KERMARREC A M and VAN STEEN M. Gossiping in distributed systems[J]. ACM SIGOPS Operating Systems Review, 2007, 41(5): 2–7. doi: 10.1145/1317379.1317381
[18]	ESPOSITO C, CASTIGLIONE A, PALMIERI F, et al. Improving the gossiping effectiveness with distributed strategic learning[J]. Future Generation Computer Systems, 2017, 71: 221–233. doi: 10.1016/j.future.2016.11.006
[19]	HOEFLER T, BARAK A, SHILOH A, et al. Corrected gossip algorithms for fast reliable broadcast on unreliable systems[C]. 2017 IEEE International Parallel and Distributed Processing Symposium, Orlando, United States, 2017: 357–366. doi: 10.1109/IPDPS.2017.36.
[20]	LI Bo, WU Junfeng, QI Hongsheng, et al. Boolean gossip networks[J]. IEEE/ACM Transactions on Networking, 2018, 26(1): 118–130. doi: 10.1109/TNET.2017.2763964
[21]	FERTIN G, PETERS J G, RAABE L, et al. Odd gossiping[J]. Discrete Applied Mathematics, 2017, 216: 550–561. doi: 10.1016/j.dam.2016.01.034
[22]	田振兴, 代杰. 基于改进Gossip协议的数据同步设计[J]. 指挥信息系统与技术, 2017, 8(5): 99–103. doi: 10.15908/j.cnki.cist.2017.05.017 TIAN Zhenxing and DAI Jie. Data synchronization design based on improved gossip protocol[J]. Command Information System and Technology, 2017, 8(5): 99–103. doi: 10.15908/j.cnki.cist.2017.05.017
[23]	HAEUPLER B, PANDURANGAN G, PELEG D, et al. Discovery through gossip[C]. The 24th ACM Symposium on Parallelism in Algorithms and Architectures, Pittsburgh, United States, 2012: 140–149. doi: 10.1145/2312005.2312031.