采用JVC算法生成枝切线的干涉相位解缠方法

王朝霞; 刘永信; 张杰; 范陈清

doi:10.11999/JEIT200086

采用JVC算法生成枝切线的干涉相位解缠方法

doi: 10.11999/JEIT200086

1.
内蒙古大学计算机学院呼和浩特 010021
2.
内蒙古大学电子信息工程学院呼和浩特 010021
3.
自然资源部第一海洋研究所青岛 266061

基金项目: 国家重点研发计划(2017YFC1405600)，自然资源部海洋遥测工程技术研究中心创新青年基金项目(2017002)

详细信息

作者简介:
王朝霞：男，1985年生，博士生，研究方向为3维高度成像技术、卫星组网观测技术等

刘永信：男，1955年生，博士，教授，博士生导师，研究方向为雷达成像技术、图像处理、信息融合等

张杰：男，1963年生，博士，研究员，博士生导师，研究方向为海洋遥感遥测技术等

范陈清：男，1983年生，副研究员，研究方向为高度遥感技术、微波雷达成像等

通讯作者:
刘永信　yxliu@imu.edu.cn

中图分类号: TN911.7; TP751.1
计量
- 文章访问数: 818
- HTML全文浏览量: 512
- PDF下载量: 55
- 被引次数: 0
出版历程
- 收稿日期: 2020-01-28
- 修回日期: 2020-12-15
- 网络出版日期: 2021-01-05
- 刊出日期: 2021-06-18

Interference Phase Unwrapping Method Using JVC Algorithm to Generate Branch Cuts

1.
College of Computer Science, Inner Mongolia University, Hohhot 010021, China
2.
College of Electronic Information Engineering, Inner Mongolia University, Hohhot 010021, China
3.
First Institute of Oceanography, Ministry of Natural Resources, Qingdao 266061, China

Funds: The National Key R&D Plan (2017YFC1405600), The Youth Innovation Fund Project in Marine Telemetry Engineering Technology Research Center of Ministry of Natural Resources (2017002)

摘要

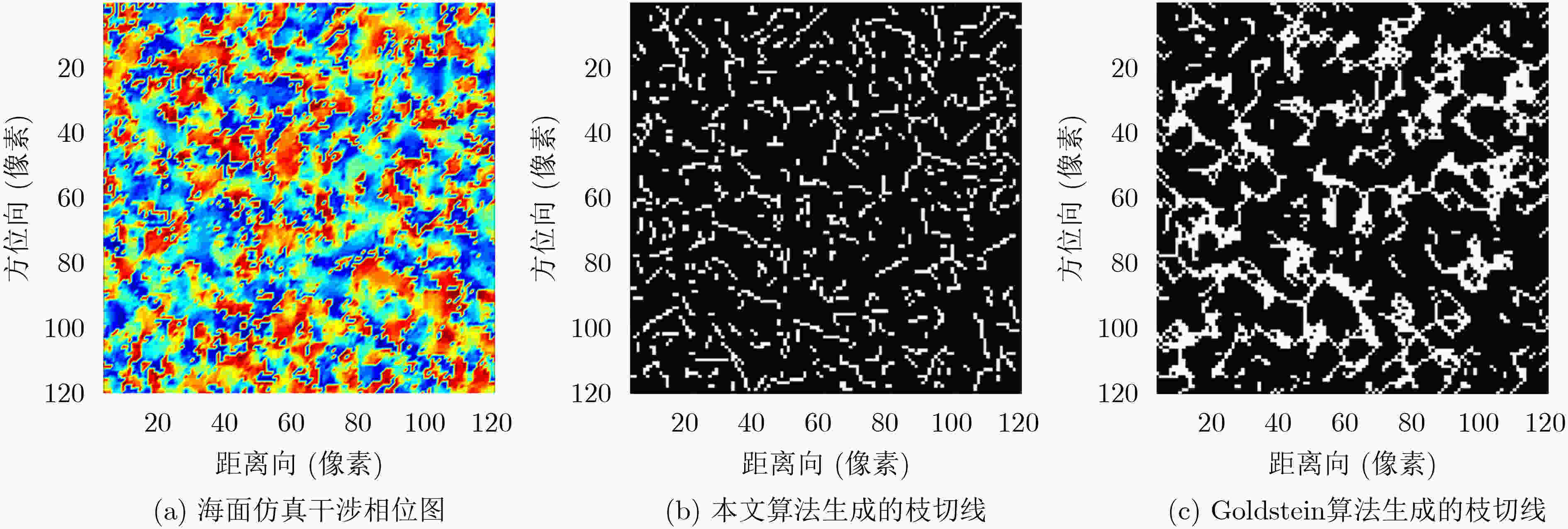
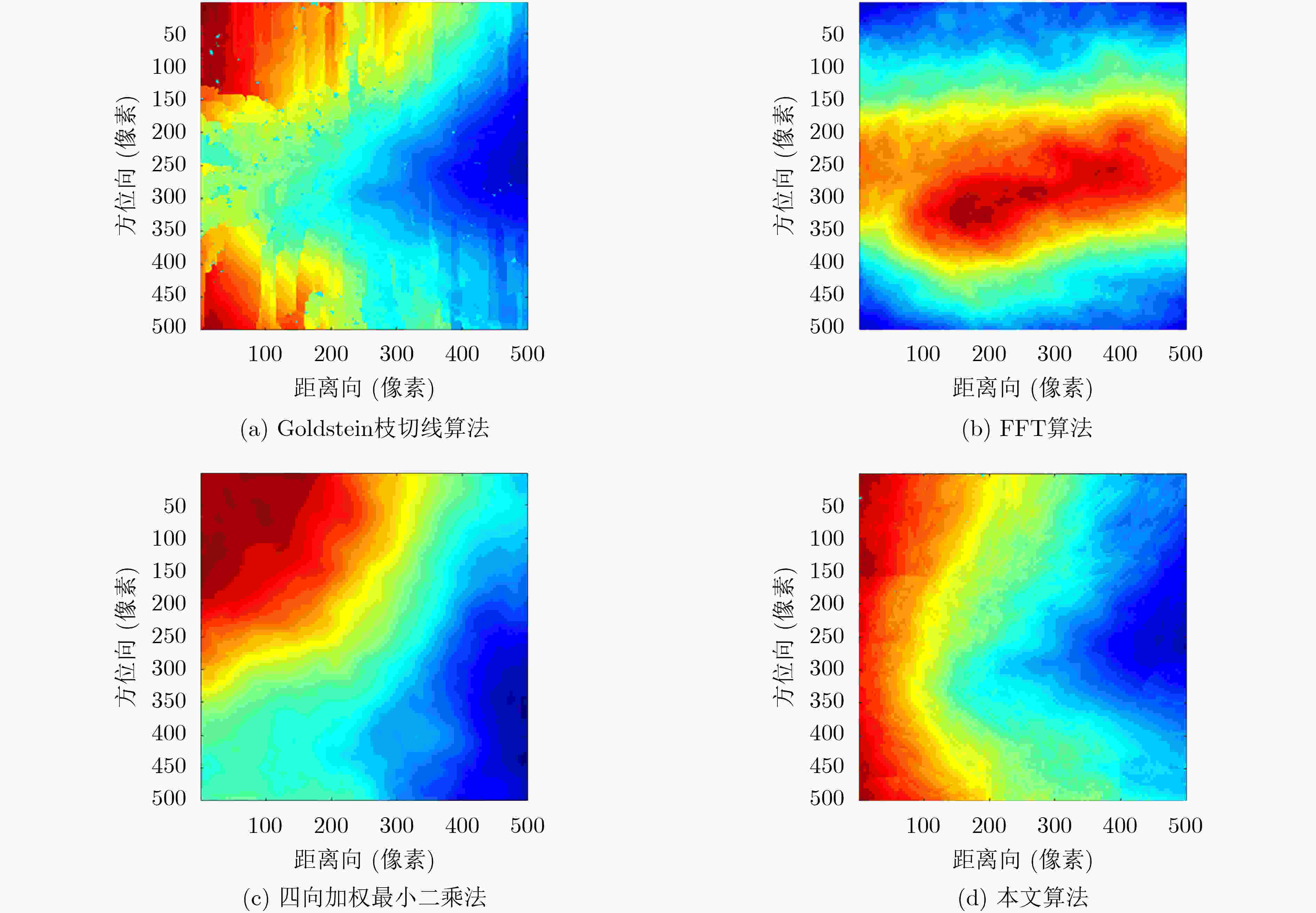
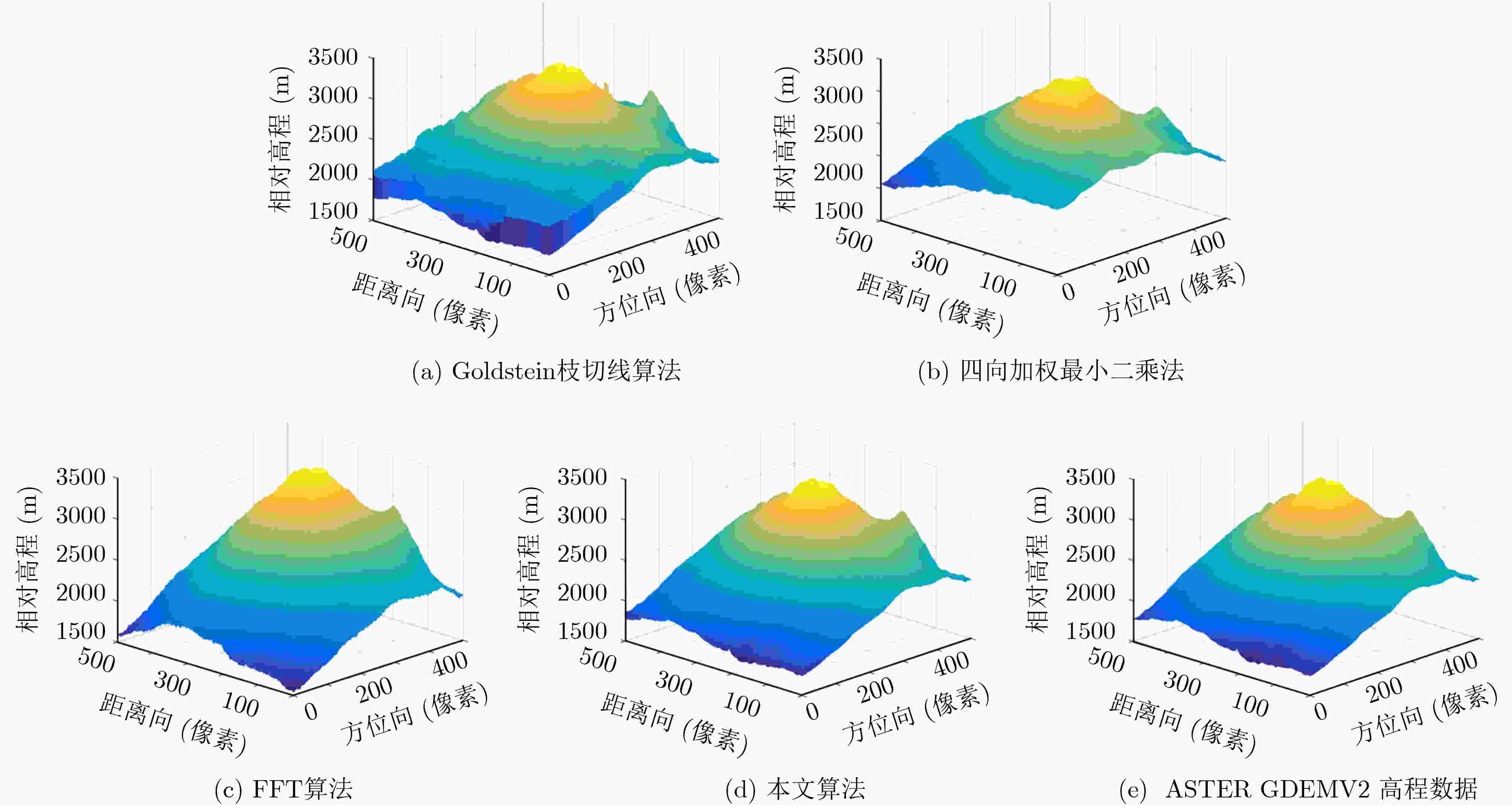
摘要: 海面高程3维成像是随着天宫二号发射而实现的技术，相位解缠是3维成像高度计高程反演的关键步骤。为改进Goldstein枝切法，缩短干涉相位图中枝切线的总长度，提升相位解缠的精确性，该文提出一种基于JVC全局最优线性分配算法生成枝切线的相位解缠方法。首先找出干涉相位图中的所有残差点并计算每一对异号残差点之间的距离；通过对比每对残差点之间的距离和各自与最近边界的距离和，确定采用JVC算法放置枝切线还是在残差点与边界之间直接放置枝切线，使得平衡枝切线的总长度最短。通过对3维成像高度计海面高程仿真干涉相位图和Etna火山地区干涉图像进行解缠实验并与其他3种算法进行对比，表明该算法的解缠结果与真实相位值误差相对较小，而且能够有效避免“孤岛现象”的产生。
- 相位解缠 /
- 3维成像高度计 /
- Jonker-Volgenant-Castanon算法 /
- 枝切线
Abstract: Three-dimensional imaging of sea surface altitude is a technology realized with the launch of Tiangong-2. Phase unwrapping is a key step in elevation inversion of three-dimensional radar imaging altimeter. In order to improve the branch cut algorithm proposed by Goldstein, shorten the total length of branch cuts in interferogram and advance the accuracy of phase unwrapping, a method that based on Jonker-Volgenant-Castanon (JVC) global optimal linear assignment algorithm to generate branch cuts is proposed in this paper. At first, all residual points in the interferogram are found out, and the distance between all opposite polarity pairs is calculated. Then, by comparing the distance between each pair of residual points and the distance sum between both of them and the nearest boundary, it is determined whether to place the branch cuts directly between the residual points and the boundaries or to use JVC algorithm. So, the shortest total length of the balanced branch cuts is obtained. The experiments of unwrapping are carried out by using the interferogram both of simulated three-dimensional imaging altimeter sea surface elevation and Etna volcano area. By comparison with the other three algorithms, it shows that the error between the unwrapping result of the proposed algorithm and the real phase value is relatively small. Also, it can void the “islanding phenomenon” effectively.
- Phase unwrapping /
- Three-dimensional imaging altimeter /
- Jonker-Volgenant-Castanon(JVC) algorithm /
- Branch cuts

HTML全文

图 1 3维成像高度计海面仿真干涉相位及其枝切线示意图

下载: 全尺寸图片幻灯片

图 2 3维成像高度计海面仿真干涉相位解缠结果

下载: 全尺寸图片幻灯片

图 3 海面仿真干涉相位图解缠后对应的相对数字高程

下载: 全尺寸图片幻灯片

图 4 Etna火山地区干涉相位及枝切线示意图

下载: 全尺寸图片幻灯片

图 5 Etna火山地区干涉相位图解缠结果

下载: 全尺寸图片幻灯片

图 6 Etna火山地区干涉相位解缠后对应的相对数字高程

下载: 全尺寸图片幻灯片

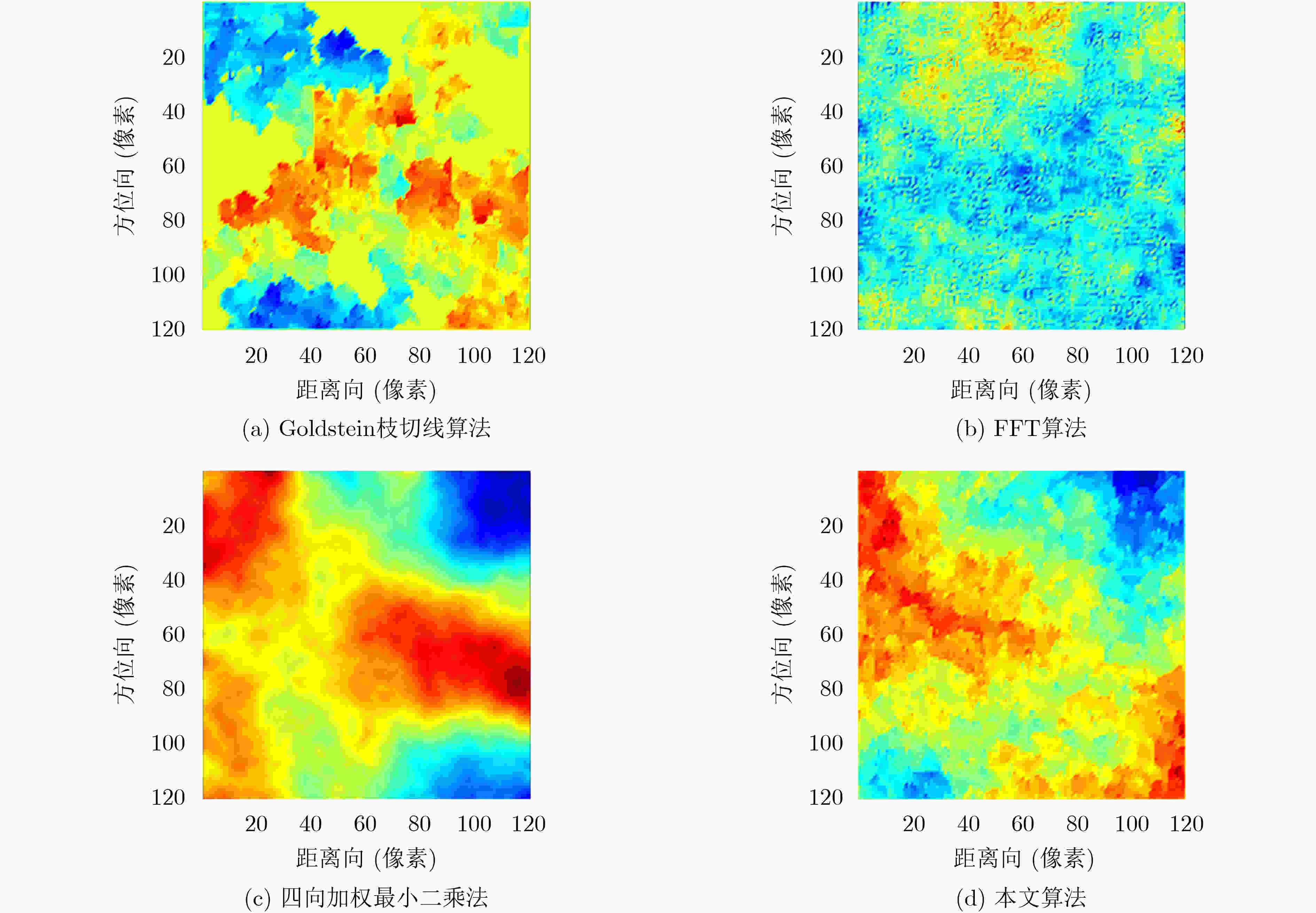
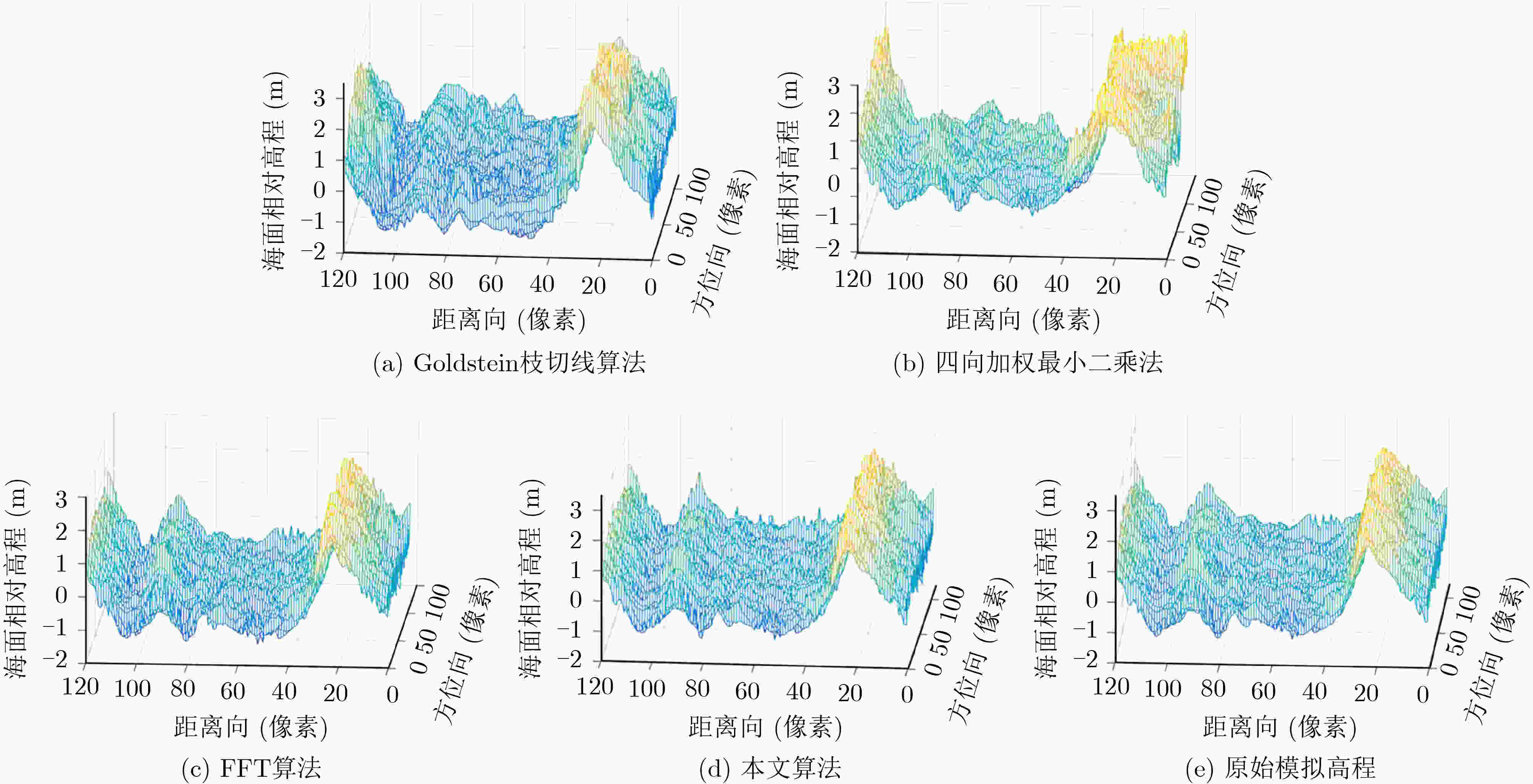
表 1 3维成像高度计海面仿真干涉相位图4种算法解缠结果对比

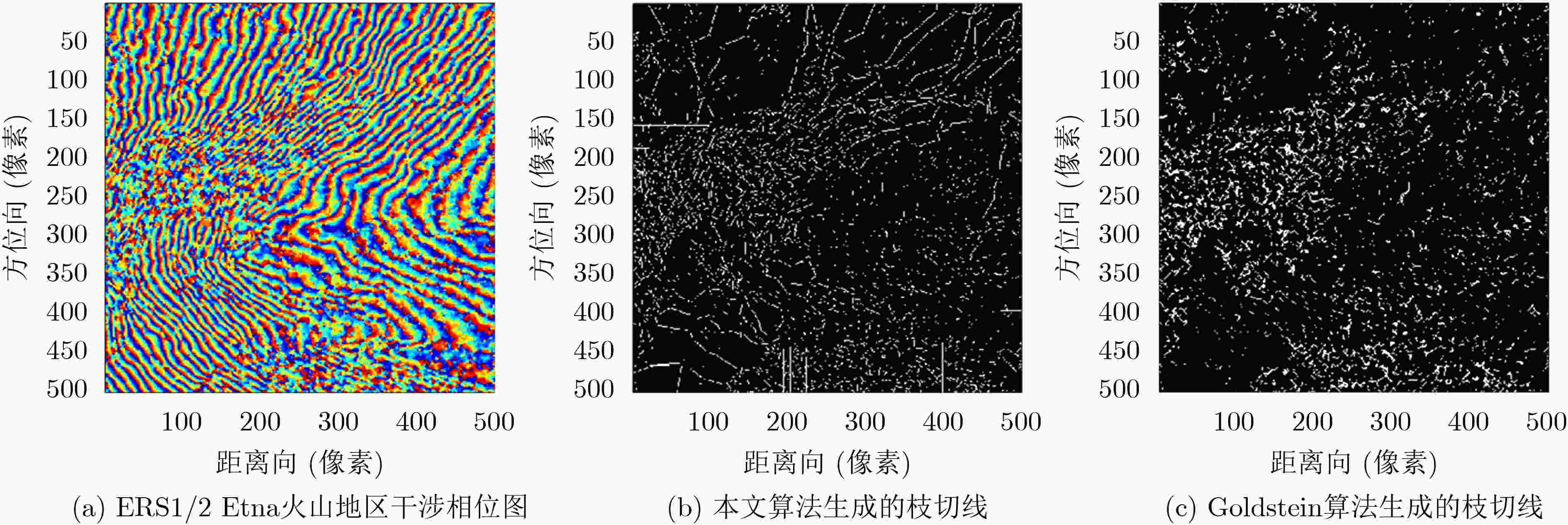
解缠算法	RMSE(m)	像素解缠率(%)	算法时间复杂度	算法运行时间(s)
Goldstein枝切线算法	0.5051	76.99	O(MN·s)	0.2685
四向加权最小二乘法	0.3110	100	O(MN·W²)	0.1018
FFT算法	0.1514	100	O(IMN·log₂MN)	0.2152
本文算法	0.0782	100	O(mn·log₂s+MN)	0.2348

下载: 导出CSV

表 2 Etna火山地区干涉相位图4种算法解缠结果对比

解缠算法	Goldstein枝切线算法	四向加权最小二乘法	FFT算法	本文算法
RMSE(m)	16.3951	33.7292	10.2693	8.7567
算法运行时间(s)	4.3245	3.3862	4.1879	4.2541

下载: 导出CSV

参考文献(16)

[1]	REN Lin, YANG Jingsong, JIA Yongjun, et al. Sea surface wind speed retrieval and validation of the interferometric imaging radar altimeter aboard the Chinese Tiangong-2 space laboratory[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2018, 11(12): 4718–4724. doi: 10.1109/JSTARS.2018.2879753
[2]	CHEVALIER L, DESROCHES D, LAIGNEL B, et al. High-resolution SWOT simulations of the macrotidal Seine estuary in different hydrodynamic conditions[J]. IEEE Geoscience and Remote Sensing Letters, 2019, 16(1): 5–9. doi: 10.1109/LGRS.2018.2862470
[3]	WANG Xian, FANG Suping, ZHU Xindong, et al. Phase unwrapping of interferometric fringes based on a mutual information quality map and phase recovery strategy[J]. Optical Engineering, 2018, 57(11): 114108. doi: 10.1117/1.OE.57.11.114108
[4]	余洁, 王少华, 焦帅, 等. 时空三维相位解缠算法改进研究[J]. 武汉大学学报: 信息科学版, 2019, 44(9): 1355–1362. doi: 10.13203/j.whugis20170414 YU Jie, WANG Shaohua, JIAO Shuai, et al. Improvement of spatio-temporal three-dimensional phase unwrapping algorithm[J]. Geomatics and Information Science of Wuhan University, 2019, 44(9): 1355–1362. doi: 10.13203/j.whugis20170414
[5]	徐华平, 高帅, 尤亚楠. 一种基于增采样的干涉SAR相位解缠方法[J]. 电子与信息学报, 2017, 39(12): 2811–2818. doi: 10.11999/JEIT170128 XU Huaping, GAO Shuai, and YOU Ya’nan. An InSAR phase unwrapping method based on incremental sampling[J]. Journal of Electronics &Information Technology, 2017, 39(12): 2811–2818. doi: 10.11999/JEIT170128
[6]	JIN Biao, GUO Jiao, WEI Pengliang, et al. Multi-baseline InSAR phase unwrapping method based on mixed-integer optimisation model[J]. IET Radar, Sonar & Navigation, 2018, 12(7): 694–701. doi: 10.1049/iet-rsn.2017.0543
[7]	GOLDSTEIN R M, ZEBKER H A, and WERNER C L. Satellite radar interferometry: Two-dimensional phase unwrapping[J]. Radio Science, 1988, 23(4): 713–720. doi: 10.1029/RS023i004p00713
[8]	GHIGLIA D C, MASTIN G A, and ROMERO L A. Cellular-automata method for phase unwrapping[J]. Journal of the Optical Society of America A, 1987, 4(1): 267–280. doi: 10.1364/JOSAA.4.000267
[9]	蒋锐, 朱岱寅, 朱兆达. 一种基于等效残差点的InSAR相位解缠绕方法[J]. 南京航空航天大学学报, 2013, 45(2): 209–216. doi: 10.16356/j.1005-2615.2013.02.007 JIANG Rui, ZHU Daiyin, and ZHU Zhaoda. Phase unwrapping approach using equivalent residues for InSAR[J]. Journal of Nanjing University of Aeronautics &Astronautics, 2013, 45(2): 209–216. doi: 10.16356/j.1005-2615.2013.02.007
[10]	张妍, 冯大政, 曲小宁, 等. 改进的枝切法在相位展开中的应用[J]. 电子科技大学学报, 2013, 42(4): 555–558. doi: 10.3969/j.issn.1001-0548.2013.04.005 ZHANG Yan, FENG Dazheng, QU Xiaoning, et al. Application of a novel branch-cut algorithm in phase unwrapping[J]. Journal of University of Electronic Science and Technology of China, 2013, 42(4): 555–558. doi: 10.3969/j.issn.1001-0548.2013.04.005
[11]	DE SOUZA J C, OLIVEIRA M E, and DOS SANTOS P A M. Branch-cut algorithm for optical phase unwrapping[J]. Optics Letters, 2015, 40(15): 3456–3459. doi: 10.1364/OL.40.003456
[12]	谢先明, 唐超. 一种融合残差点信息的改进的多基线InSAR高程重建方法[J]. 电子与信息学报, 2018, 40(5): 1159–1165. doi: 10.11999/JEIT170775 XIE Xianming and TANG Chao. An improved multi-baseline InSAR height reconstruction method based on interferogram residues[J]. Journal of Electronics &Information Technology, 2018, 40(5): 1159–1165. doi: 10.11999/JEIT170775
[13]	张晖, 刘永信, 张杰, 等. 地波雷达与自动识别系统目标点迹最优关联算法[J]. 电子与信息学报, 2015, 37(3): 619–624. doi: 10.11999/JEIT140678 ZHANG Hui, LIU Yongxin, ZHANG Jie, et al. Target point tracks optimal association algorithm with surface wave radar and automatic identification system[J]. Journal of Electronics &Information Technology, 2015, 37(3): 619–624. doi: 10.11999/JEIT140678
[14]	李芹, 刘维, 王道档, 等. 基于二阶质量权的四向剪切相位解包裹算法[J]. 光电子∙激光, 2018, 29(6): 618–626. doi: 10.16136/j.joel.2018.06.0250 LI Qin, LIU Wei, WANG Daodang, et al. Four-direction least-square phase unwrapping algorithm based on shearing interferometry and second derivative of quality weight[J]. Journal of Optoelectronics∙Laser, 2018, 29(6): 618–626. doi: 10.16136/j.joel.2018.06.0250
[15]	WANG Yong and QIAN Guangzhao. Novel approach for InSAR sensors imaging via gradient-based algorithm for the sparse signal reconstruction[J]. IEEE Sensors Journal, 2018, 18(6): 2385–2394. doi: 10.1109/JSEN.2018.2791568
[16]	LI Hui and ZHAO Jiayang. Evaluation of the newly released worldwide AW3D30 DEM over typical landforms of China using two global DEMs and ICESat/GLAS data[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2018, 11(11): 4430–4440. doi: 10.1109/JSTARS.2018.2874361