Quadrature Multicarrier Noise Reduction Differential Chaos Shift Keying System
-
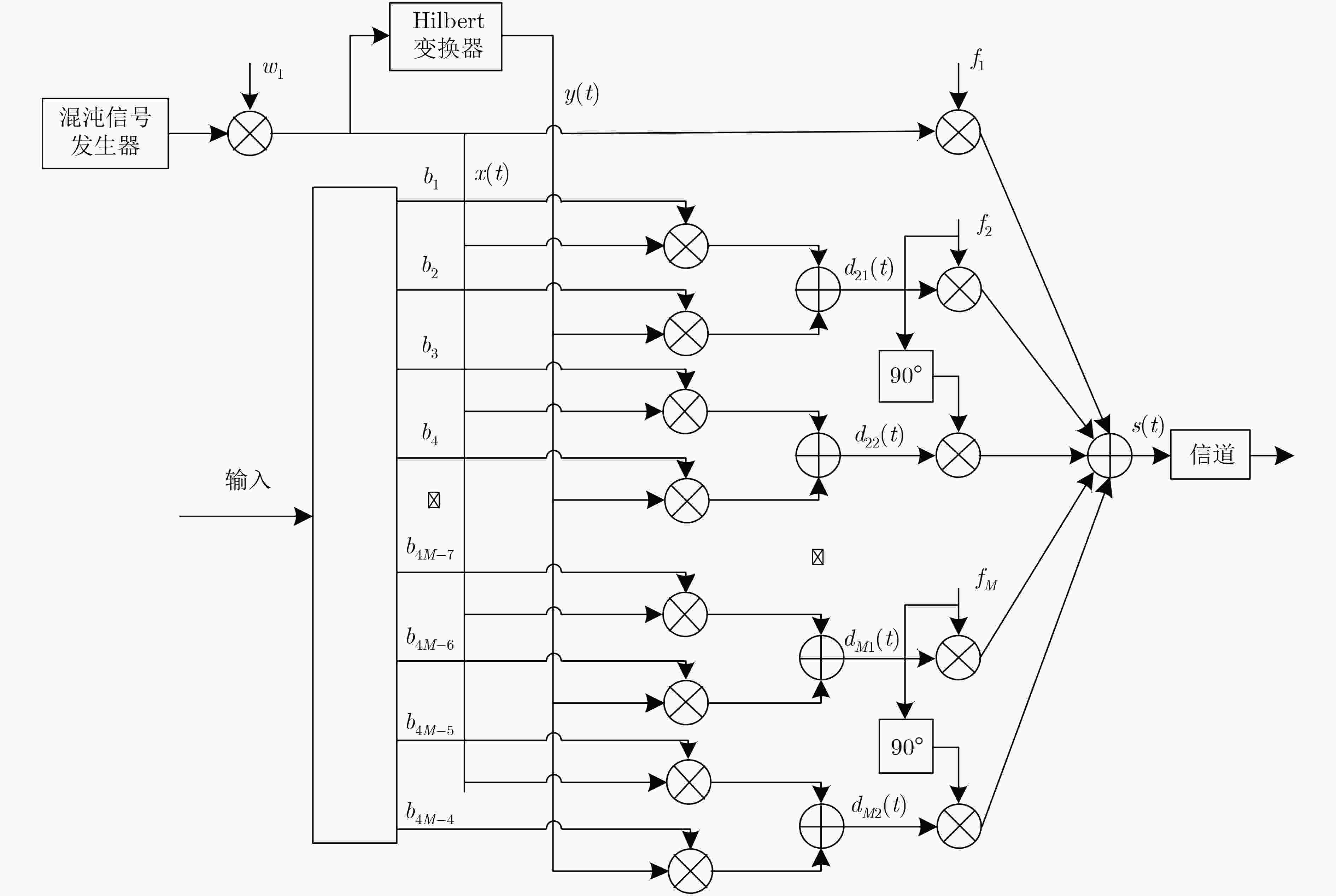
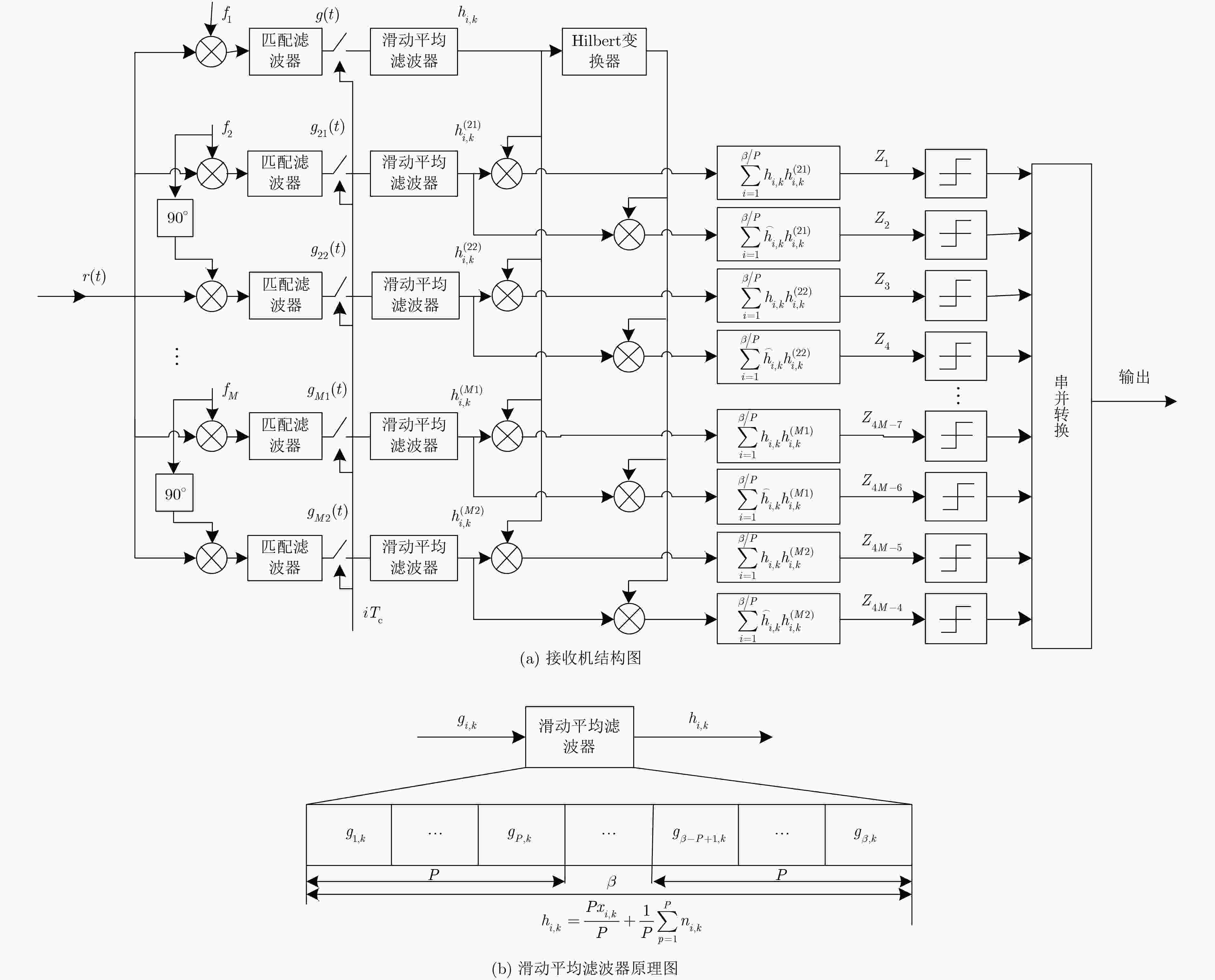
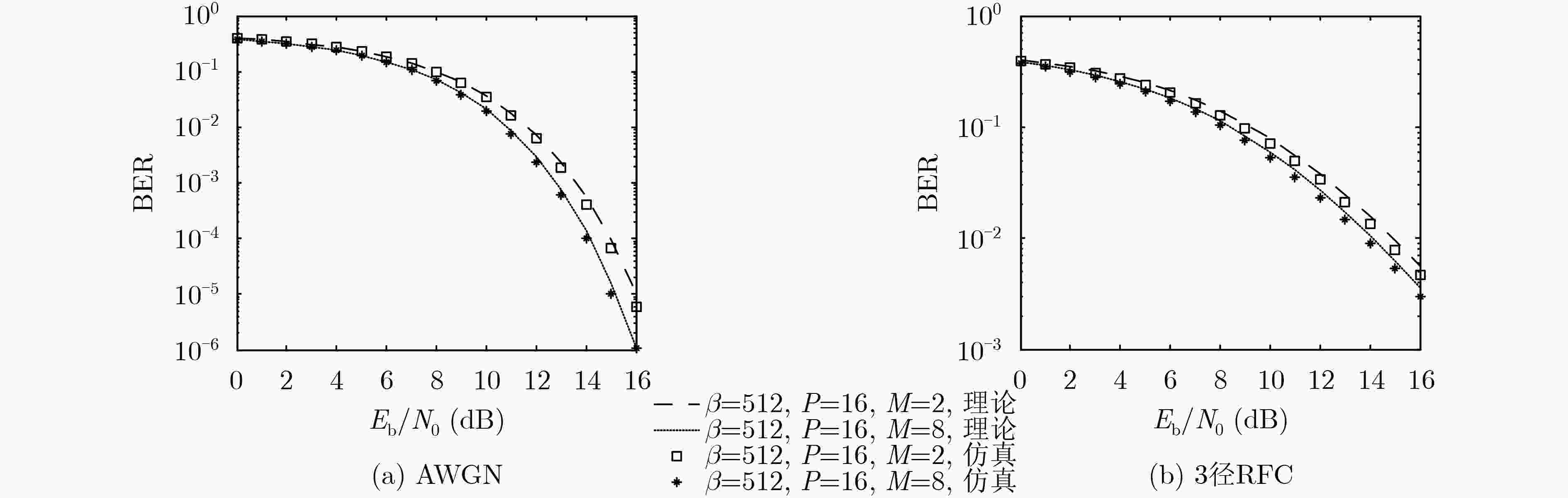
摘要: 为解决多载波差分混沌移位键控(MC-DCSK)系统传输速率低和误码性能差的缺点,该文提出一种正交多载波降噪差分混沌移位键控(QMC-NR-DCSK)系统。在发送端,预定义载波用于发送参考信号,剩余M-1个不同中心频率的载波及其经正交调制技术后得到的频率相同但相位正交的载波都用于传输信息信号,此外,通过进一步引入Hilbert变换,将系统的频带利用率和传输速率提升为MC-DCSK系统的4倍。在接收端引入滑动平均滤波器的降噪操作降低了噪声的方差,从而改善了系统误码性能。推导了QMC-NR-DCSK系统在加性高斯白噪声(AWGN)信道和多径瑞利衰落(RFC)信道下的比特误码率公式并进行了仿真。仿真结果和理论分析表明:QMC-NR-DCSK系统能有效提升传输速率、带宽效率和误码性能,为该系统应用于多载波无线通信提供理论参考。Abstract: The major drawbacks of MultiCarrier Differential Chaos Shift Keying (MC-DCSK) system are relating to low data rate and poor bit error performance. Therefore a Quadrature MultiCarrier Noise Reduction Differential Chaos Shift Keying (QMC-NR-DCSK) system is proposed to improve the performances of MC-DCSK system. At the transmitter, reference signal is transmitted on the predefined carrier. While the remaining M-1 carriers and the carriers with orthogonal phase at the same frequency are all used to transmit information signals by using Quadrature Modulation technology, and the data-rate to bandwidth ratio and transmission rate of which are four times higher than that of MC-DCSK system by further introducing Hilbert transformation. The noise reduction operation of the moving average filter is introduced to reduce the variance of noise at the receiver, thereby improving the bit error performance of the QMC-NR-DCSK system. The bit error rate formula and simulations of QMC-NR-DCSK system under Additive White Gaussian Noise (AWGN) channel and multi-path Rayleigh Fading Channel (RFC) are carried out respectively. The results show that QMC-NR-DCSK system can effectively improve the transmission rate, data-rate to bandwidth ratio and bit error performance, which provides a theoretical reference for the application of the multicarrier communication systems.
-
表 1 几种多载波系统间TR, EE和EB的对比
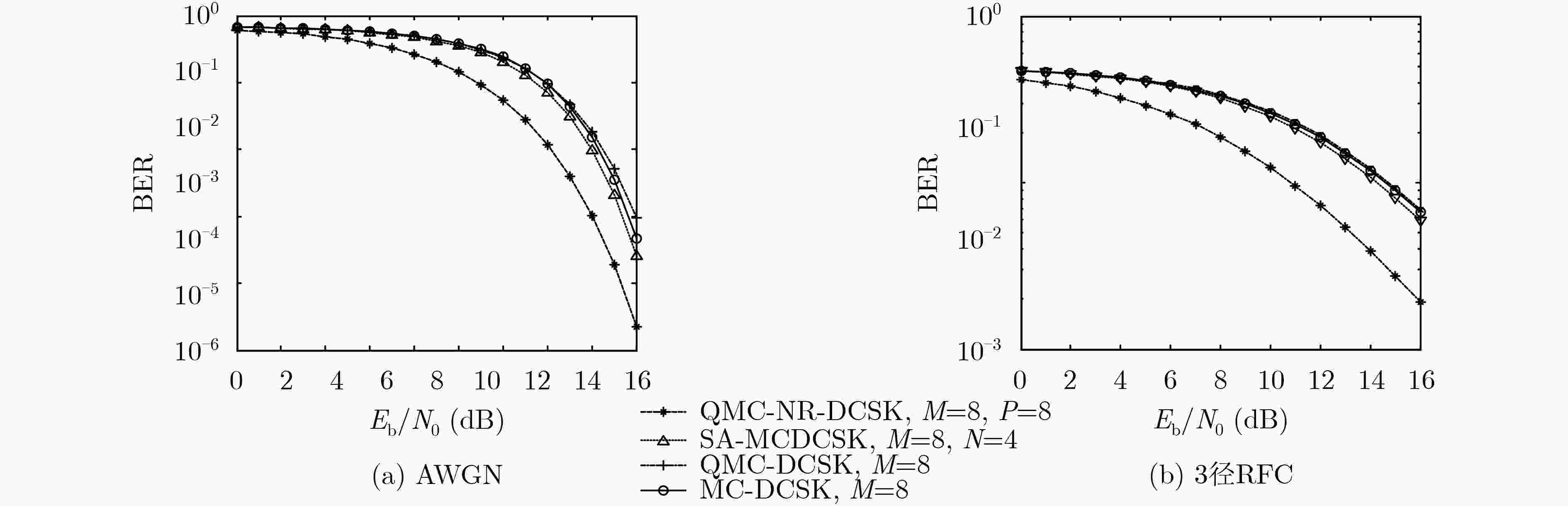
系统名称 传输速率${\rm{TR}}$ 能量效率${\rm{EE}}$ 带宽效率${\rm{BE}}$ MC-DCSK ${ {(M - 1)} / \beta}$ ${ {M - 1} / \beta}$ ${{(M - 1)} / {(M\beta (1 + \alpha ))}}$ QMC-DCSK ${ {2(M - 1)} / \beta}$ ${{(M - 1)} / {(M - {1 / 2})}}$ ${{2(M - 1)} / {(M\beta (1 + \alpha ))}}$ SA-MCDCSK ${ {(M - N)} / \beta}$ ${{(M - N)} / M}$ ${{(M - N)} / {(M\beta (1 + \alpha ))}}$ QMC-NR-DCSK $4{ {(M - 1)} / \beta}$ ${{(M - 1)} / {(M - {3 / 4})}}$ ${{4(M - 1)} / {(M\beta (1 + \alpha ))}}$ 表 2 多径RFC信道参数取值表
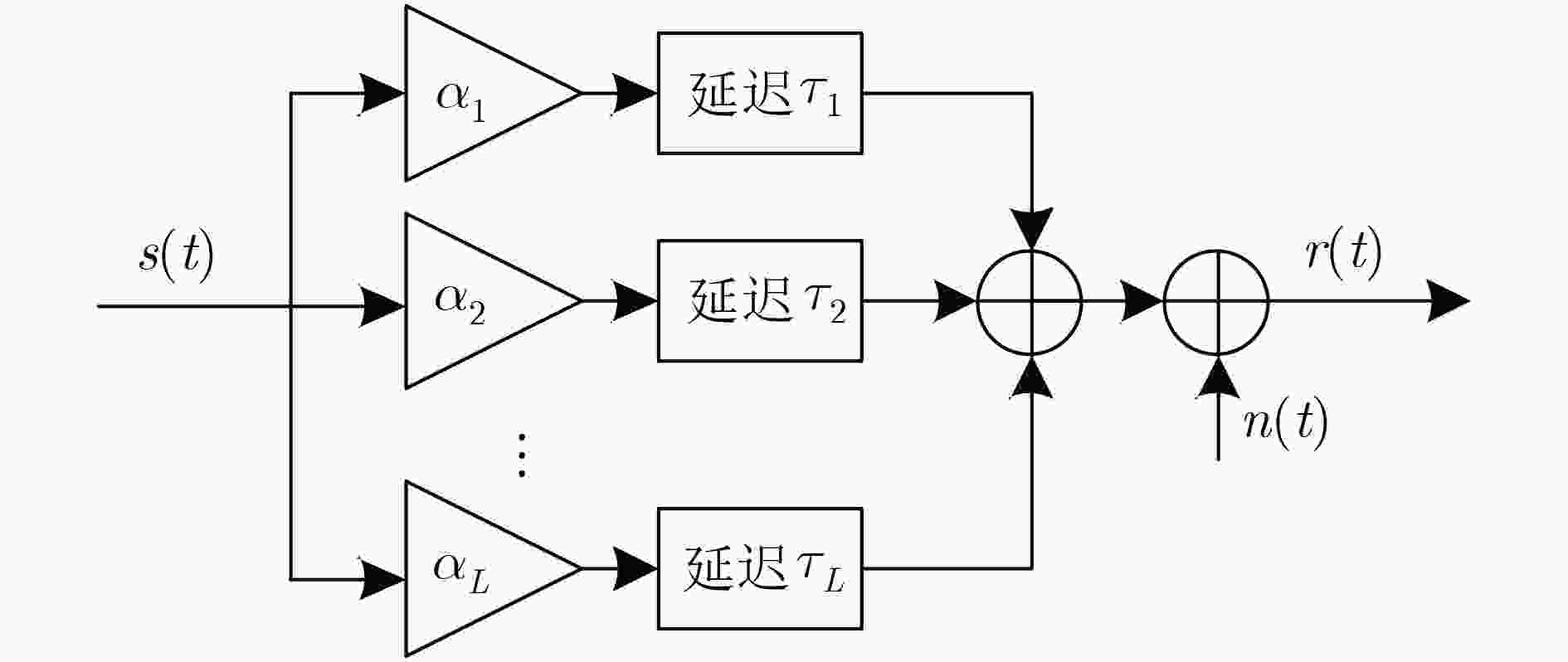
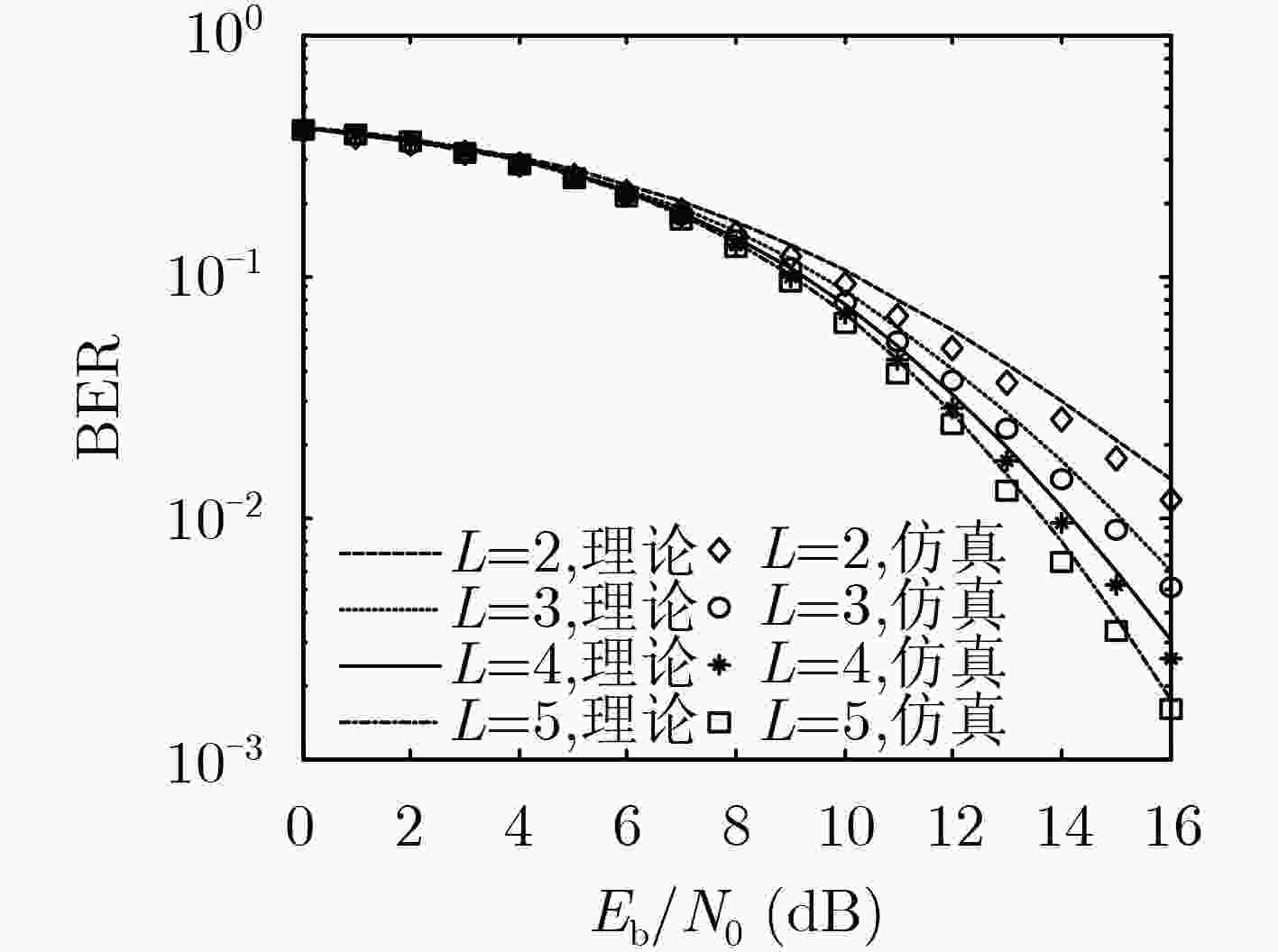
L $E\left[ {\alpha _l^2} \right]$ ${\tau _l}$ L=2 1/2, 1/2 0, 1 L=3 1/3, 1/3, 1/3 0, 1, 2 L=4 1/4, 1/4, 1/4, 1/4 0, 1, 2, 3 L=5 1/5, 1/5, 1/5, 1/5, 1/5 0, 1, 2, 3, 4 -
QUYEN N X and KYAMAKYA K. Chaos-based Digital Communication Systems with Low Data-rate Wireless Applications[M]. KYAMAKYA K, MATHIS W, STOOP R, et al. Recent Advances in Nonlinear Dynamics and Synchronization. Cham, Germany: Springer, 2017: 239–269. doi: 10.1007/978-3-319-58996-1_11. KADDOUM G. Wireless chaos-based communication systems: A comprehensive survey[J]. IEEE Access, 2016, 4: 2621–2648. doi: 10.1109/access.2016.2572730 ÇIÇEK S, KOCAMAZ U E, and UYAROGLU Y. Secure chaotic communication with Jerk chaotic system using sliding mode control method and its real circuit implementation[J]. Iranian Journal of Science and Technology, Transactions of Electrical Engineering, 2019, 43(3): 687–698. doi: 10.1007/s40998-019-00184-9 GALIAS Z and MAGGIO G M. Quadrature chaos-shift keying: Theory and performance analysis[J]. IEEE Transactions on Circuits and Systems I: Fundamental Theory and Applications, 2001, 48(12): 1510–1519. doi: 10.1109/TCSI.2001.972858 张刚, 赵畅畅, 张天骐. 短参考正交多用户差分混沌键控方案的性能分析[J]. 电子与信息学报, 2019, 41(9): 2055–2062. doi: 10.11999/JEIT181038ZHANG Gang, ZHAO Changchang, and ZHANG Tianqi. Performance analysis of short reference orthogonal multiuser differential chaotic shift keying scheme[J]. Journal of Electronics &Information Technology, 2019, 41(9): 2055–2062. doi: 10.11999/JEIT181038 NGUYEN X Q. On the study of a quadrature DCSK modulation scheme for cognitive radio[J]. International Journal of Bifurcation and Chaos, 2017, 27(9): 1750135. doi: 10.1142/S0218127417501358 LYU Yibo, WANG Lin, CAI Guofa, et al. Iterative receiver for M-ary DCSK systems[J]. IEEE Transactions on Communications, 2015, 63(11): 3929–3936. doi: 10.1109/TCOMM.2015.2425877 张琳, 徐位凯, 王琳, 等. 码复用差分混沌键控性能分析与同步算法[J]. 重庆邮电大学学报: 自然科学版, 2016, 28(3): 330–336. doi: 10.3979/j.issn.1673-825X.2016.03.008ZHANG Lin, XU Weikai, WANG Lin, et al. Performance analysis and synchronization algorithm for CS-DCSK system[J]. Journal of Chongqing University of Posts and Telecommunications:Natural Science Edition, 2016, 28(3): 330–336. doi: 10.3979/j.issn.1673-825X.2016.03.008 WANG Shaonan, LIU Yingjie, and MA Weijiao. Design of a novel frequency division scheme for DCSK chaos communication system[C]. 2017 3rd International Conference on Information Management (ICIM), Chengdu, China, 2017: 317–321. doi: 10.1109/INFOMAN.2017.7950400. 张刚, 陈和祥, 张天骐. 多用户降噪差分混沌键控通信方案[J]. 电子与信息学报, 2019, 41(2): 362–368. doi: 10.11999/JEIT171173ZHANG Gang, CHEN Hexiang, and ZHANG Tianqi. A multiuser noise reduction differential chaos shift keying system[J]. Journal of Electronics &Information Technology, 2019, 41(2): 362–368. doi: 10.11999/JEIT171173 KADDOUM G, RICHARDSON F D, and GAGNON F. Design and analysis of a multi-carrier differential chaos shift keying communication system[J]. IEEE Transactions on Communications, 2013, 61(8): 3281–3291. doi: 10.1109/TCOMM.2013.071013.130225 BAO Jiyu, XU Weikai, WANG Lin, et al. Performance analysis and sub-carriers power allocation for MC-QCSK[C]. 2015 International Conference on Wireless Communications & Signal Processing (WCSP), Nanjing, China, 2015: 1–5. doi: 10.1109/WCSP.2015.7341173. QUYEN N X and PHAM C K. Quadrature multi-carrier DCSK: A high-efficiency scheme for radio communications[C]. 2017 International Conference on Advanced Technologies for Communications (ATC), Quy Nhon, Vietnam, 2017: 186–191. doi: 10.1109/ATC.2017.8167614. YANG Hua, JIANG Guoping, TANG W K S, et al. Multi-carrier differential chaos shift keying system with subcarriers allocation for noise reduction[J]. IEEE Transactions on Circuits and Systems II: Express Briefs, 2018, 65(11): 1733–1737. doi: 10.1109/TCSII.2017.2752754 CAI Guofa, WANG Lin, and CHEN Guanrong. Capacity of the non-coherent DCSK system over rayleigh fading channel[J]. IET Communications, 2016, 10(18): 2663–2669. doi: 10.1049/iet-com.2016.0487 MANDAL S, BANERJEE S. Analysis and CMOS implementation of a chaos-based communication system[J]. IEEE Transactions on Circuits and Systems I: Regular Papers, 2004, 51(9): 1708–1722. doi: 10.1109/TCSI.2004.834482 LONG N H, QUYEN N X, and VAN YEM V. Design of an improved multi-carrier DCSK system for digital communications[C]. 2017 International Conference on Recent Advances in Signal Processing, Telecommunications & Computing, Da Nang, Vietnam, 2017: 211–216. doi: 10.1109/SIGTELCOM.2017.7849824. -





 下载:
下载:






 下载:
下载:
