Collaborative Parameter Update Based on Average Variance Reduction of Historical Gradients
-
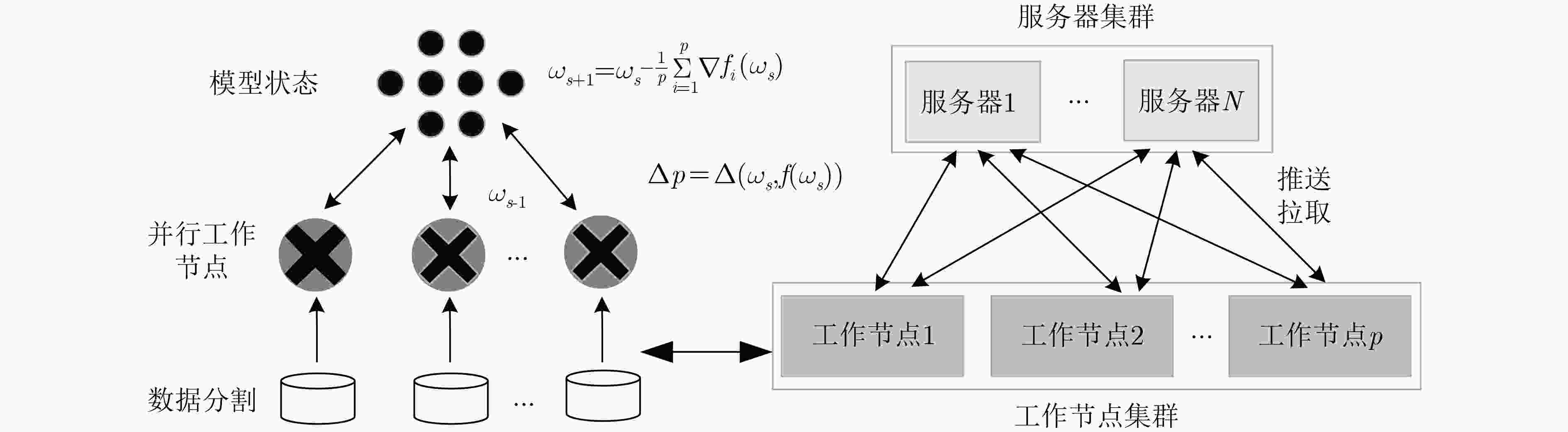
摘要: 随机梯度下降算法(SGD)随机使用一个样本估计梯度,造成较大的方差,使机器学习模型收敛减慢且训练不稳定。该文提出一种基于方差缩减的分布式SGD,命名为DisSAGD。该方法采用历史梯度平均方差缩减来更新机器学习模型中的参数,不需要完全梯度计算或额外存储,而是通过使用异步通信协议来共享跨节点的参数。为了解决全局参数分发存在的“更新滞后”问题,该文采用具有加速因子的学习速率和自适应采样策略:一方面当参数偏离最优值时,增大加速因子,加快收敛速度;另一方面,当一个工作节点比其他工作节点快时,为下一次迭代采样更多样本,使工作节点有更多时间来计算局部梯度。实验表明:DisSAGD显著减少了循环迭代的等待时间,加速了算法的收敛,其收敛速度比对照方法更快,在分布式集群中可以获得近似线性的加速。Abstract: The Stochastic Gradient Descent (SGD) algorithm randomly picks up a sample to estimate gradients, creating big variance which reduces the convergence speed and makes the training unstable. A Distributed SGD based on Average variance reduction, called DisSAGD is proposed. The method uses the average variance reduction based on historical gradients to update parameters in the machine learning model, requiring little gradient calculation and additional storage, but using the asynchronous communication protocol to share parameters across nodes. In order to solve the “update staleness” problem of global parameter distribution, a learning rate with an acceleration factor and an adaptive sampling strategy are included: on the one hand, when the parameter deviates from the optimal value, the acceleration factor is increased to speed up the convergence; on the other hand, when one work node is faster than the other ones, more samples are sampled for the next iteration, so that the node has more time to calculate the local gradient. Experiments show that the DisSAGD reduces significantly the waiting time of loop iterations, accelerates the convergence of the algorithm being faster than that of the controlled methods, and obtains almost linear acceleration in distributed cluster environments.
-
Key words:
- Gradient descent /
- Machine learning /
- Distributed cluster /
- Adaptive sampling /
- Variance reduction
-
表 1 基于历史梯度平均方差缩减算法
输入:learning rate $\lambda $. 输出:$\omega $ and $g$ for next epoch. (1) Initialize $\omega $ using plain SGD for 1 epoch; (2) while not converged do (3) $\overline \omega \leftarrow 0$; (4) $\overline g \leftarrow 0$; (5) for $t$= 0, 1, ···, T do (6) Randomly sample ${i_t} = \{ 1,2,··· ,m\}$ without replacement; (7) $\overline \omega \leftarrow \frac{1}{m}\displaystyle\sum\limits_{i = 1}^m { {\omega _i} }$; (8) $\overline g \leftarrow \frac{1}{m}\displaystyle\sum\limits_{i = 1}^m {\nabla {f_i}({\omega _i})}$; (9) Update $g$ and $\omega $ using equation(1) and equation(3),
respectively;(10) end (11) end 表 2 DisSAGD算法的伪代码
输入:${D_1},{D_2}, ··· ,{D_p}$. 输出:${\omega _1},{\omega _2}, ··· ,{\omega _p}$. (1) Initialize ${\omega _p}$; (2) for s = 1, 2, ···, N do (3) for each node $k \in \{ 1,2, ··· ,p\} $do (4) Call subroutine avr_hg($\lambda $); (5) end (6) Return all ${\omega _{k,t}}$ and ${f_{k,t}}(\omega )$ from node k to server; (7) Compute ${\omega ^{s - 1} } = \dfrac{1}{k}\displaystyle\sum\limits_{i = 1}^k { {\omega _i} }$ and $f(\omega )$ using equation(4)
on the server side;(8) ${\omega ^s} = {\omega ^{s - 1} } - {\lambda _{s - 1} }\dfrac{1}{k}\displaystyle\sum\limits_{i = 1}^k {\nabla {f_i}(\omega )}$; (9) end (10) ${\omega _p} \leftarrow {\omega ^s}$; 表 3 模型的F1值
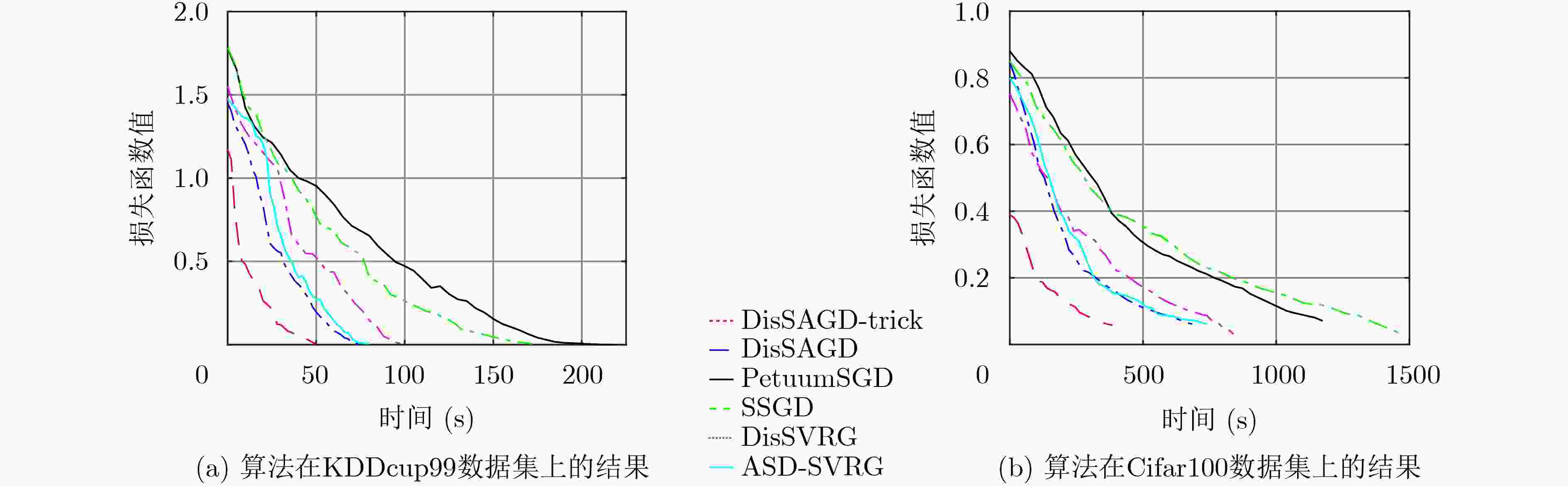
SVHN Cifar100 KDDcup99 PetuumSGD 0.9547 0.6684 0.9335 SSGD 0.9675 0.6691 0.9471 DisSVRG 0.9688 0.6776 0.9441 ASD-SVRG 0.9831 0.6834 0.9512 DisSAGD 0.9827 0.6902 0.9508 DisSAGD-tricks 0.9982 0.7086 0.9588 -
周辉林, 欧阳韬, 刘健. 基于随机平均梯度下降和对比源反演的非线性逆散射算法研究[J]. 电子与信息学报, 2020, 42(8): 2053–2058. doi: 10.11999/JEIT190566ZHOU Huilin, OUYANG Tao, and LIU Jian. Stochastic average gradient descent contrast source inversion based nonlinear inverse scattering method for complex objects reconstruction[J]. Journal of Electronics &Information Technology, 2020, 42(8): 2053–2058. doi: 10.11999/JEIT190566 XING E P, HO Q, DAI Wei, et al. Petuum: A new platform for distributed machine learning on big data[J]. IEEE Transactions on Big Data, 2015, 1(2): 49–67. doi: 10.1109/TBDATA.2015.2472014 HO Qirong, CIPAR J, CUI Henggang, et al. More effective distributed ml via a stale synchronous parallel parameter server[C]. Advances in Neural Information Processing Systems, Stateline, USA, 2013: 1223–1231. SHI Hang, ZHAO Yue, ZHANG Bofeng, et al. A free stale synchronous parallel strategy for distributed machine learning[C]. The 2019 International Conference on Big Data Engineering, Hong Kong, China, 2019: 23–29. doi: 10.1145/3341620.3341625. ZHAO Xing, AN Aijun, LIU Junfeng, et al. Dynamic stale synchronous parallel distributed training for deep learning[C]. 2019 IEEE 39th International Conference on Distributed Computing Systems (ICDCS), Dallas, USA, 2019: 1507–1517. doi: 10.1109/ICDCS.2019.00150. DEAN J, CORRADO G S, MONGA R, et al. Large scale distributed deep networks[C]. The 25th International Conference on Neural Information Processing Systems, Red Hook, USA, 2012: 1223–1231. 赵小强, 宋昭漾. 多级跳线连接的深度残差网络超分辨率重建[J]. 电子与信息学报, 2019, 41(10): 2501–2508. doi: 10.11999/JEIT190036ZHAO Xiaoqiang and SONG Zhaoyang. Super-resolution reconstruction of deep residual network with multi-level skip connections[J]. Journal of Electronics &Information Technology, 2019, 41(10): 2501–2508. doi: 10.11999/JEIT190036 LI Mu, ANDERSEN D G, PARK J W, et al. Scaling distributed machine learning with the parameter server[C]. The 2014 International Conference on Big Data Science and Computing, Beijing, China, 2014: 583–598. https://doi.org/10.1145/2640087.2644155. ZHANG Ruiliang, ZHENG Shuai, and KWOK J T. Asynchronous distributed semi-stochastic gradient optimization[C]. The Thirtieth AAAI Conference on Artificial Intelligence, Phoenix, USA, 2016: 2323–2329. XIE Pengtao, KIM J K, ZHOU Yi, et al. Distributed machine learning via sufficient factor broadcasting[J]. arXiv: 1511. 08486, 2015. LI Mu, ZHANG Tong, CHEN Yuqiang, et al. Efficient mini-batch training for stochastic optimization[C]. The 20th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, New York, USA, 2014: 661–670. doi: 10.1145/2623330.2623612. WU Jiaxiang, HUANG Weidong, HUANG Junzhou, et al. Error compensated quantized SGD and its applications to large-scale distributed optimization[C]. The 35th International Conference on Machine Learning, Stockholm, The Kingdom of Sweden, 2018. LE ROUX N, SCHMIDT M, and BACH F. A stochastic gradient method with an exponential convergence rate for finite training sets[C]. The 26th Annual Conference on Neural Information Processing Systems, Lake Tahoe, USA, 2012: 2663–2671. DEFAZIO A, BACH F, and LACOSTE-JULIEN S. SAGA: A fast incremental gradient method with support for non-strongly convex composite objectives[C]. The 27th International Conference on Neural Information Processing Systems, Cambridge, USA, 2014: 1646–1654. BAN Zhihua, LIU Jianguo, and CAO Li. Superpixel segmentation using Gaussian mixture model[J]. IEEE Transactions on Image Processing, 2018, 27(8): 4105–4117. doi: 10.1109/TIP.2018.2836306 WANG Pengfei, LIU Risheng, ZHENG Nenggan, et al. Asynchronous proximal stochastic gradient algorithm for composition optimization problems[J]. Proceedings of the AAAI Conference on Artificial Intelligence, 2019, 33(1): 1633–1640. doi: 10.1609/aaai.v33i01.33011633 FERRANTI L, PU Ye, JONES C N, et al. SVR-AMA: An asynchronous alternating minimization algorithm with variance reduction for model predictive control applications[J]. IEEE Transactions on Automatic Control, 2019, 64(5): 1800–1815. doi: 10.1109/TAC.2018.2849566 邵言剑, 陶卿, 姜纪远, 等. 一种求解强凸优化问题的最优随机算法[J]. 软件学报, 2014, 25(9): 2160–2171. doi: 10.13328/j.cnki.jos.004633SHAO Yanjian, TAO Qing, JIANG Jiyuan, et al. Stochastic algorithm with optimal convergence rate for strongly convex optimization problems[J]. Journal of Software, 2014, 25(9): 2160–2171. doi: 10.13328/j.cnki.jos.004633 赵海涛, 程慧玲, 丁仪, 等. 基于深度学习的车联边缘网络交通事故风险预测算法研究[J]. 电子与信息学报, 2020, 42(1): 50–57. doi: 10.11999/JEIT190595ZHAO Haitao, CHENG Huiling, DING Yi, et al. Research on traffic accident risk prediction algorithm of edge internet of vehicles based on deep learning[J]. Journal of Electronics &Information Technology, 2020, 42(1): 50–57. doi: 10.11999/JEIT190595 RAMAZANLI I, NGUYEN H, PHAM H, et al. Adaptive sampling distributed stochastic variance reduced gradient for heterogeneous distributed datasets[J]. arXiv: 2002. 08528, 2020. SUSSMAN D M. CellGPU: Massively parallel simulations of dynamic vertex models[J]. Computer Physics Communications, 2017, 219: 400–406. doi: 10.1016/j.cpc.2017.06.001 -





 下载:
下载:


 下载:
下载:
