一种网络RTK参考站模糊度快速解算方法

王守华; 吴黎荣; 尤志奇; 付文涛; 纪元法

doi:10.11999/JEIT200059

一种网络RTK参考站模糊度快速解算方法

doi: 10.11999/JEIT200059

王守华^{1, 2, 3, ,},
吴黎荣^{2, 3},
尤志奇^{2, 3},
付文涛³,
纪元法^{2, 3}

1.
桂林电子科技大学信息与通信学院桂林 541004
2.
桂林电子科技大学认知无线电与信息处理省部共建教育部重点实验室桂林 541004
3.
卫星导航定位与位置服务国家地方联合工程研究中心桂林 541004

基金项目: 认知无线电与信息处理省部共建教育部重点实验室主任基金(CRKL190105)，广西自然科学基金(2018JJA170154)，广西科技项目(AA17202033)，广西区级研究生教育创新计划项目(YCSW2021180)

详细信息

作者简介:
王守华：1975年生，男，博士生，教授，研究方向为信号处理、卫星导航

吴黎荣：1993年生，男，硕士生，研究方向为网络RTK

尤志奇：1996年生，男，硕士生，研究方向为北斗高精度定位

付文涛：1989年生，男，硕士，研究方向为卫星导航

纪元法：1975年生，男，博士，教授，研究方向为卫星导航、信号处理

通讯作者:
王守华　wshgluet@163.com

中图分类号: TN927
计量
- 文章访问数: 928
- HTML全文浏览量: 455
- PDF下载量: 67
- 被引次数: 0
出版历程
- 收稿日期: 2020-10-15
- 修回日期: 2021-04-06
- 网络出版日期: 2021-06-03
- 刊出日期: 2021-08-10

A Fast Ambiguity Solution Method for Network RTK Reference Station

Shouhua WANG^{1, 2, 3
, ,},
Lirong WU^{2, 3},
Zhiqi YOU^{2, 3},
Wentao FU³,
Yuanfa JI^{2, 3}

1.
College of Information and Communication, Guilin University of Electronic Technology, Guilin 541004, China
2.
Key Laboratory of Cognitive Radio and Information Processing of Guilin University of Electronic Technology, Ministry of Education, Guilin 541004, China
3.
National Engineering Research Center for Satellite Navigation, Positioning and Position Service, Guilin 541004, China

Funds: The Key Laboratory of Cognitive Radio and Information Processing, Ministry of Education (Guilin University of Electronic Technology (CRKL190105), The Foundation of Guangxi Natural Science Foundation (2018JJA170154), The Department of Science and Technology of Guangxi Zhuang Autonomous Region (AA17202033), The Innovation Project of Guangxi Graduate Education (YCSW2021180)

摘要

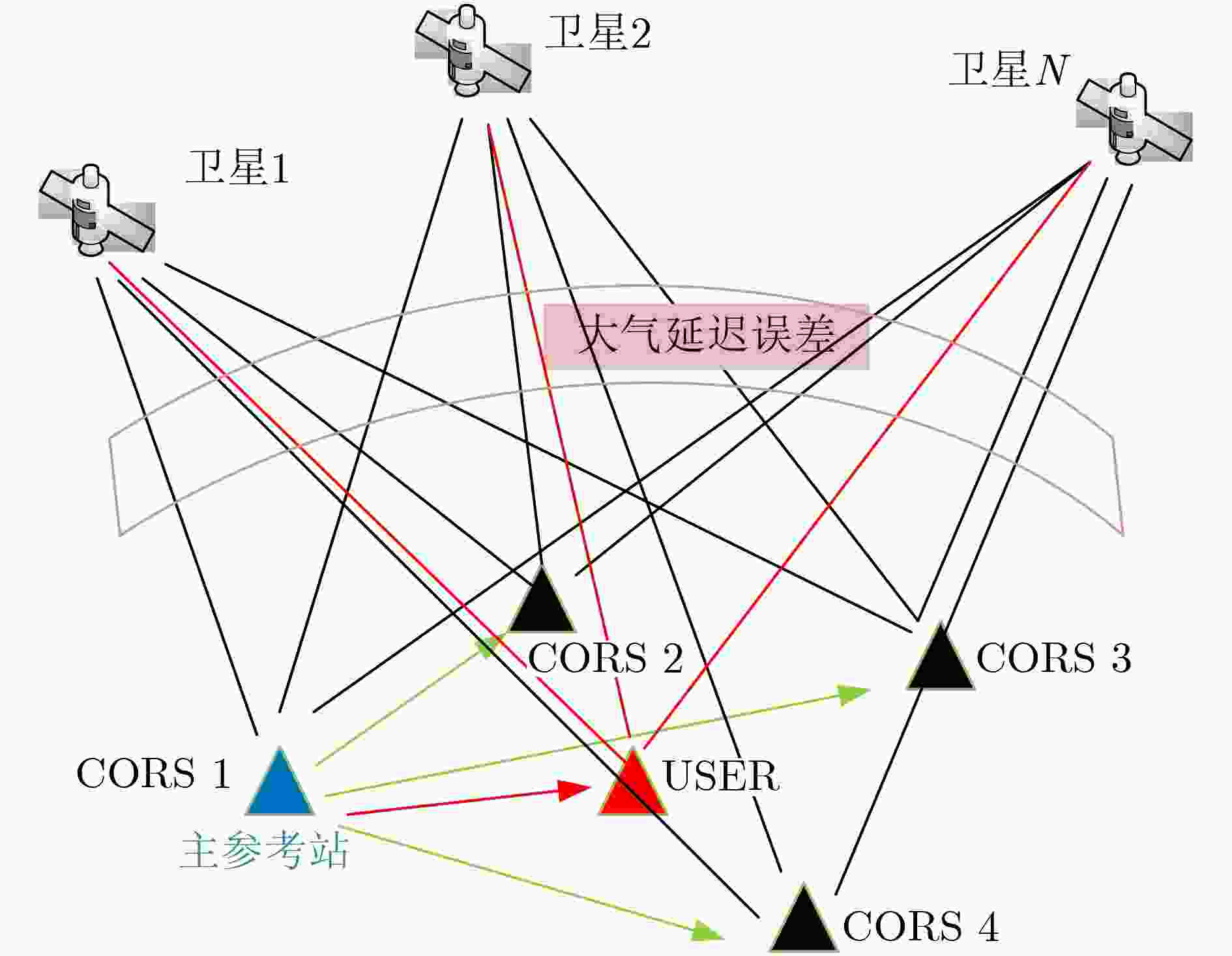
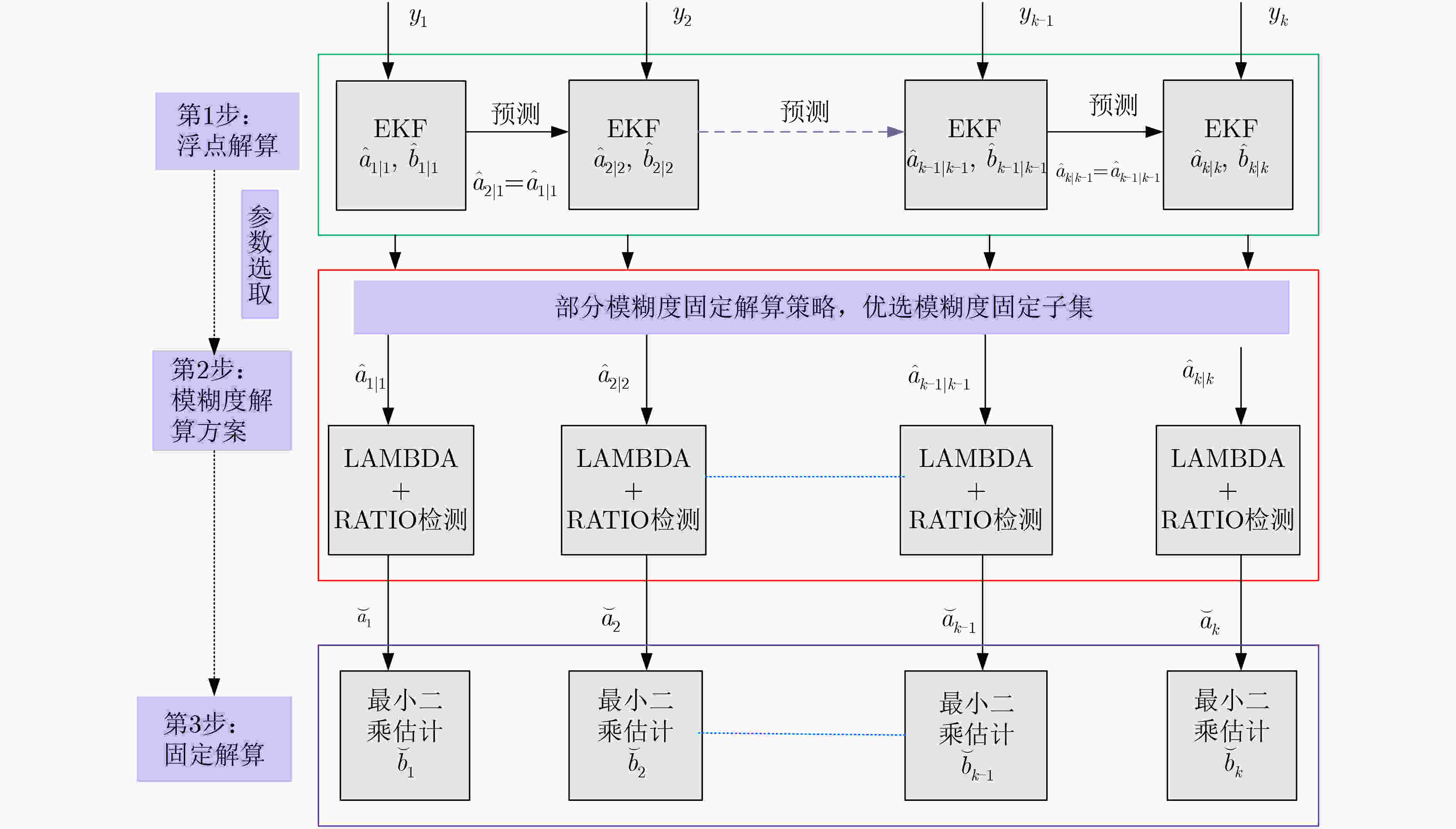
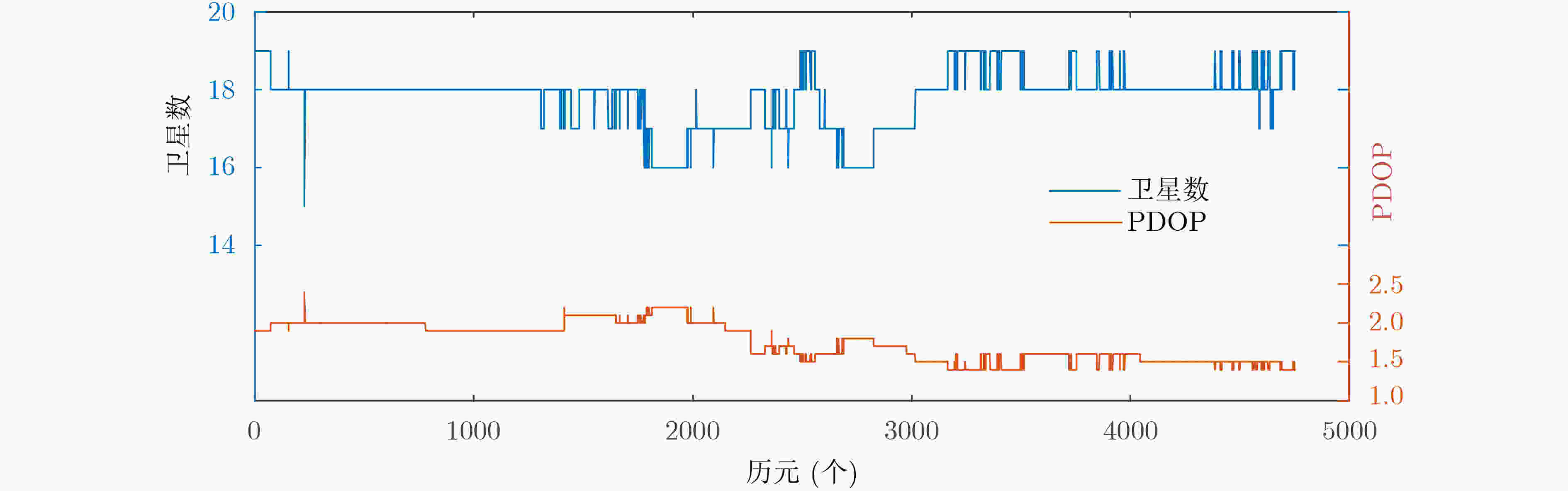
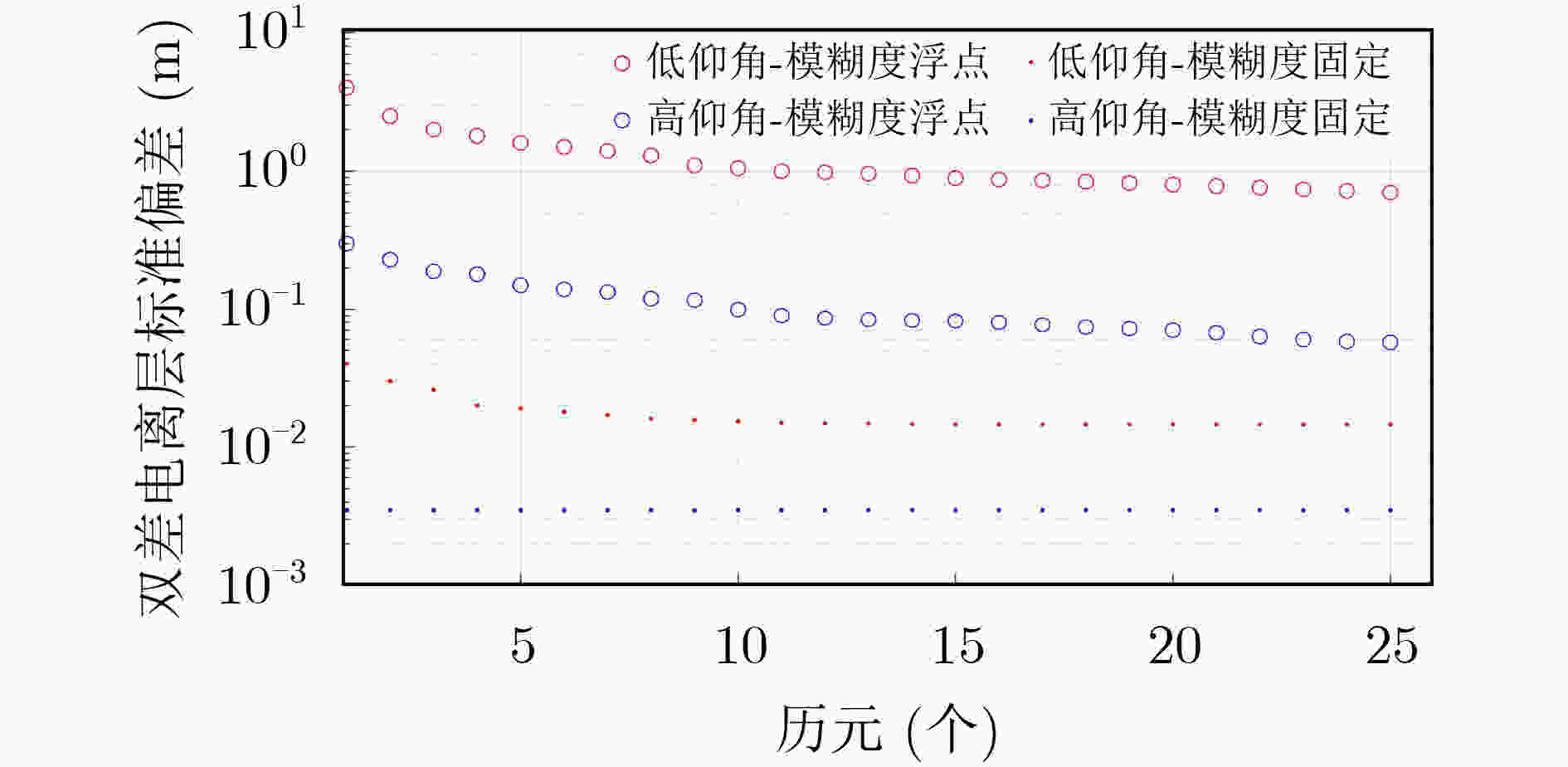
摘要: 针对由于存在大气因素的干扰，网络载波相位差分技术(RTK)参考站模糊度解算会受到影响，同时当新卫星升至预先设置的截止高度角以上时，需要较长的初始化收敛时间，该文提出一种网络RTK参考站模糊度快速解算方法。该方法先利用电离层加权策略，辅助基线模糊度的快速解算，再采用扩展卡尔曼滤波(EKF)技术估计浮点模糊度，利用部分模糊度解算方法，最后通过最小二乘模糊度降相关(LAMBDA)算法和比率(RATIO)检测对模糊度进行固定解算。实验结果表明，该方法可以显著提高网络RTK参考站模糊度的固定率和缩短初始化收敛时间。
- 网络RTK /
- 模糊度解算 /
- 部分模糊度固定 /
- 电离层加权法
Abstract: Due to the interference of atmospheric factors, the ambiguity resolution of network Real Time kinematic (RTK) reference stations is affected, and when new satellites rise above the preset cutoff height, a longer initialization convergence time is required. A fast ambiguity solution method for Network RTK reference stations is proposed. Firstly, the ionosphere weighting strategy is used to assist the fast resolution of baseline ambiguity. Then, Extended Kalman Filter(EKF)is used to estimate ambiguity floating solution; The partial ambiguity solution method is adopted. Finally, the ambiguities are fixed in combination with Least squares AMBiguity Decorrelation Adjustment(LAMBDA) and RATIO detection. Experiments results show that this method can significantly improve the ambiguity fixation rate of network RTK reference stations and shorten the initialization convergence time.
- Network RTK /
- Ambiguity resolution /
- Partial ambiguity fixed /
- Ionosphere weighted method

HTML全文

图 1 网络RTK定位原理图

下载: 全尺寸图片幻灯片

图 2 网络RTK参考站模糊度解算步骤流程图

下载: 全尺寸图片幻灯片

图 3 未加权电离层模型处理结果

下载: 全尺寸图片幻灯片

图 4 电离层加权模型处理结果

下载: 全尺寸图片幻灯片

图 5 不同模糊度解算方法的RATIO值对比

下载: 全尺寸图片幻灯片

图 6 可见卫星数量及空间分布PDOP序列图

下载: 全尺寸图片幻灯片

图 7 全模糊度固定解算方法的3维基线序列

下载: 全尺寸图片幻灯片

8 不同模糊度解算方法的3维基线序列

下载: 全尺寸图片幻灯片

图 9 模糊度固定前后的双差电离层延迟的标准偏差示例

下载: 全尺寸图片幻灯片

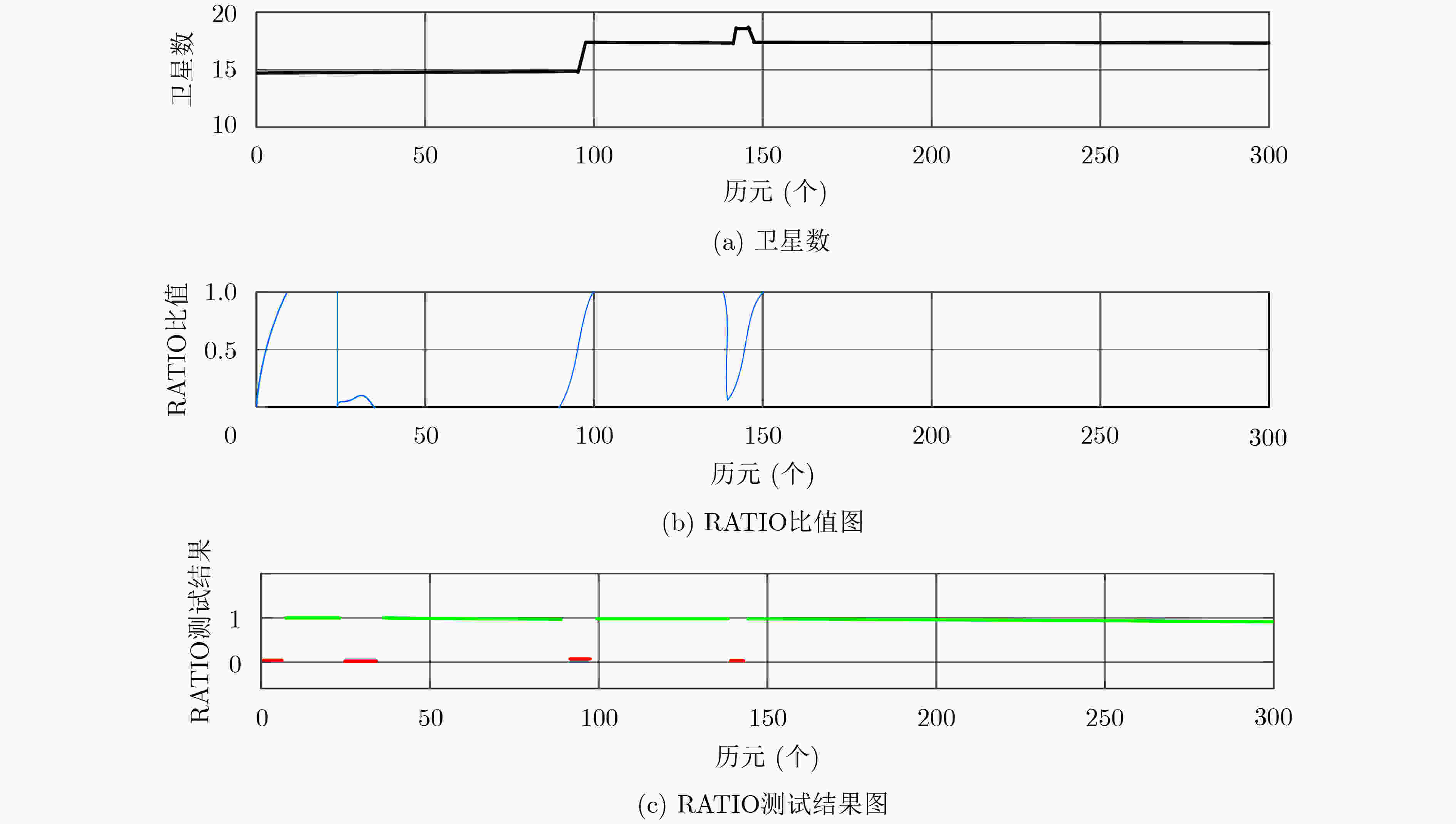
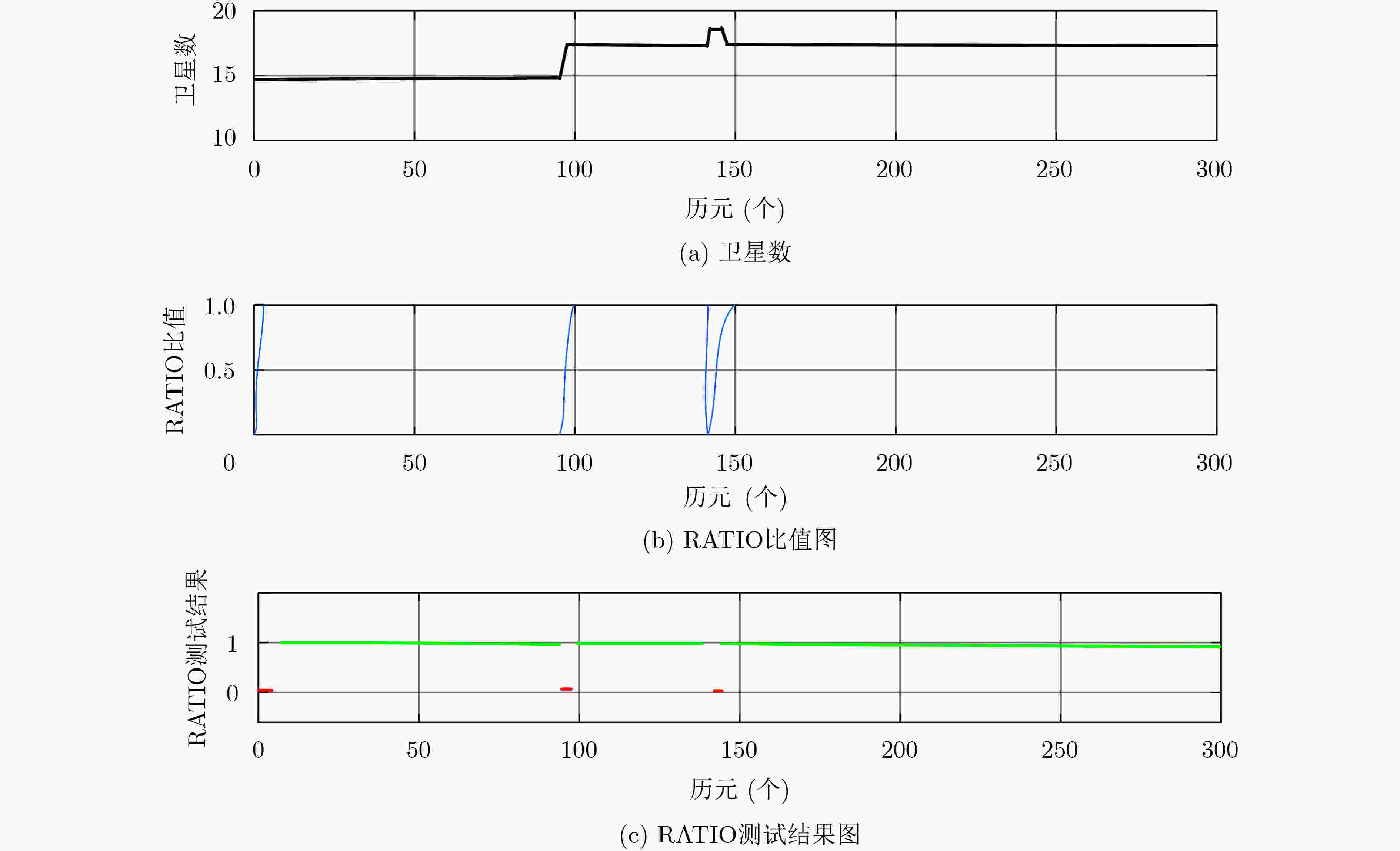
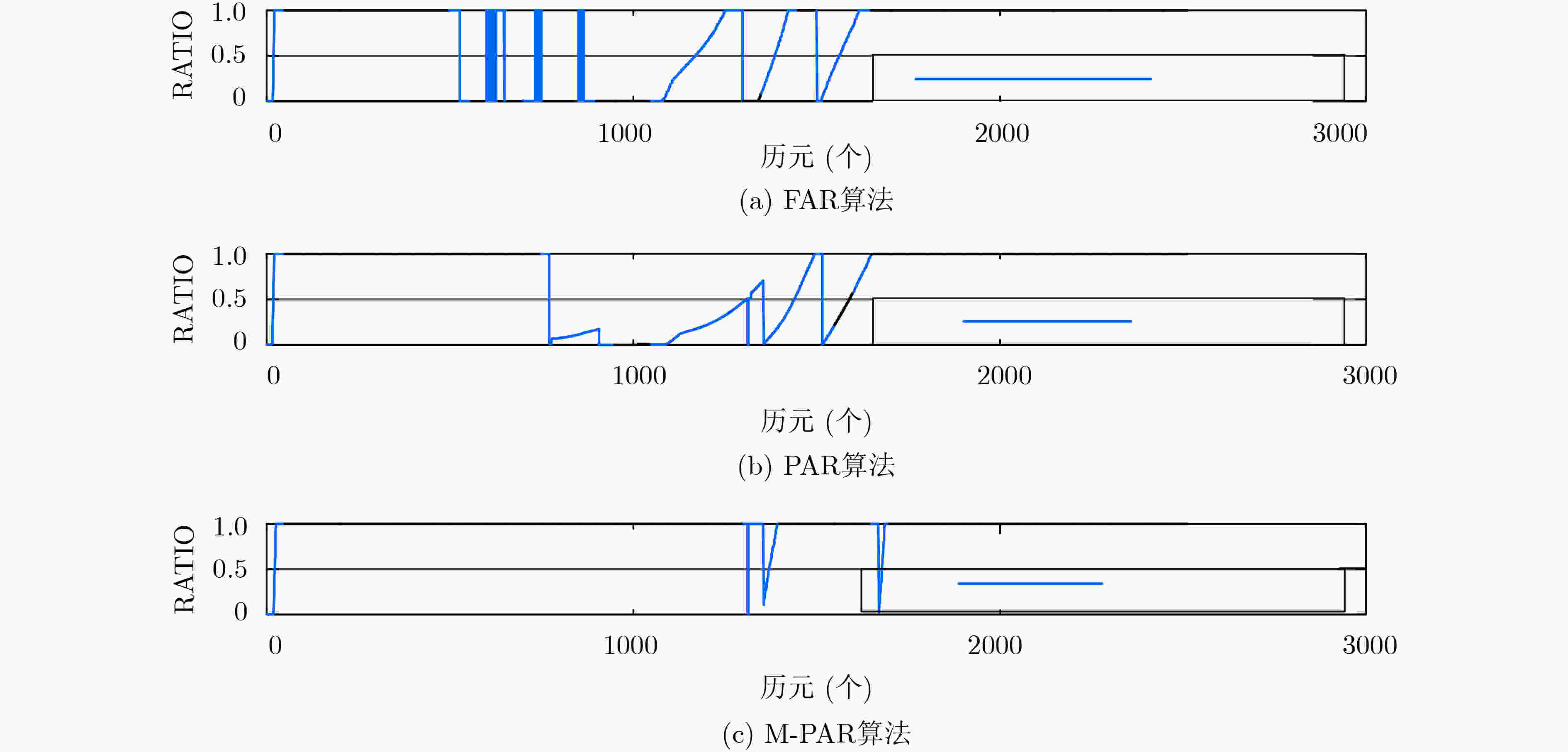
表 1 不同解算方法的固定率和初始化时间对比

模糊度解算方法	模糊度固定率(%)	初始化时间(s)
LAMBDA(全)	18.6	3680
FAR	82.3	270
PAR	92.6	20
M-PAR	97.6	20

下载: 导出CSV

表 2 不同解算方法的定位结果绝对误差(m)

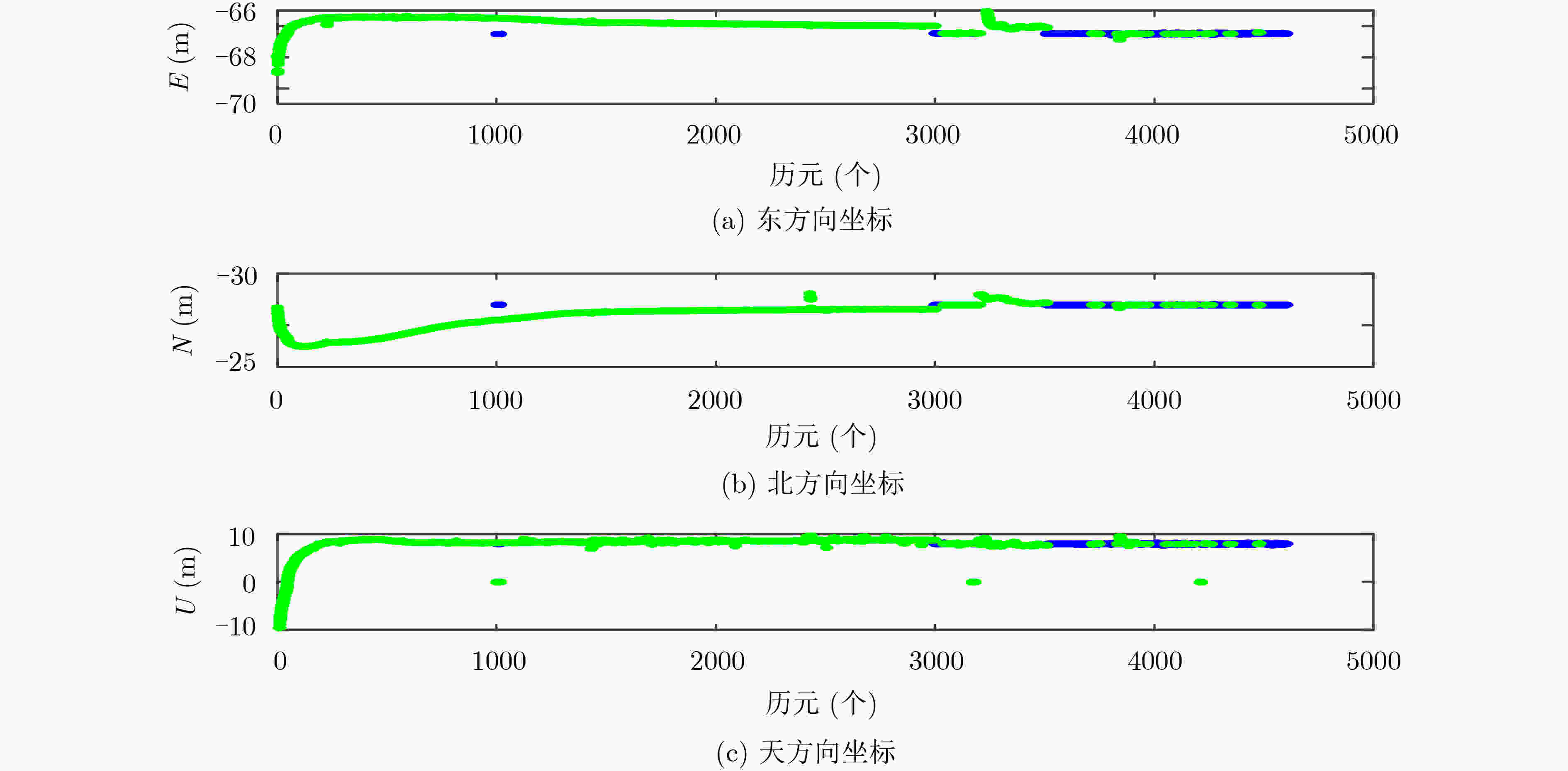
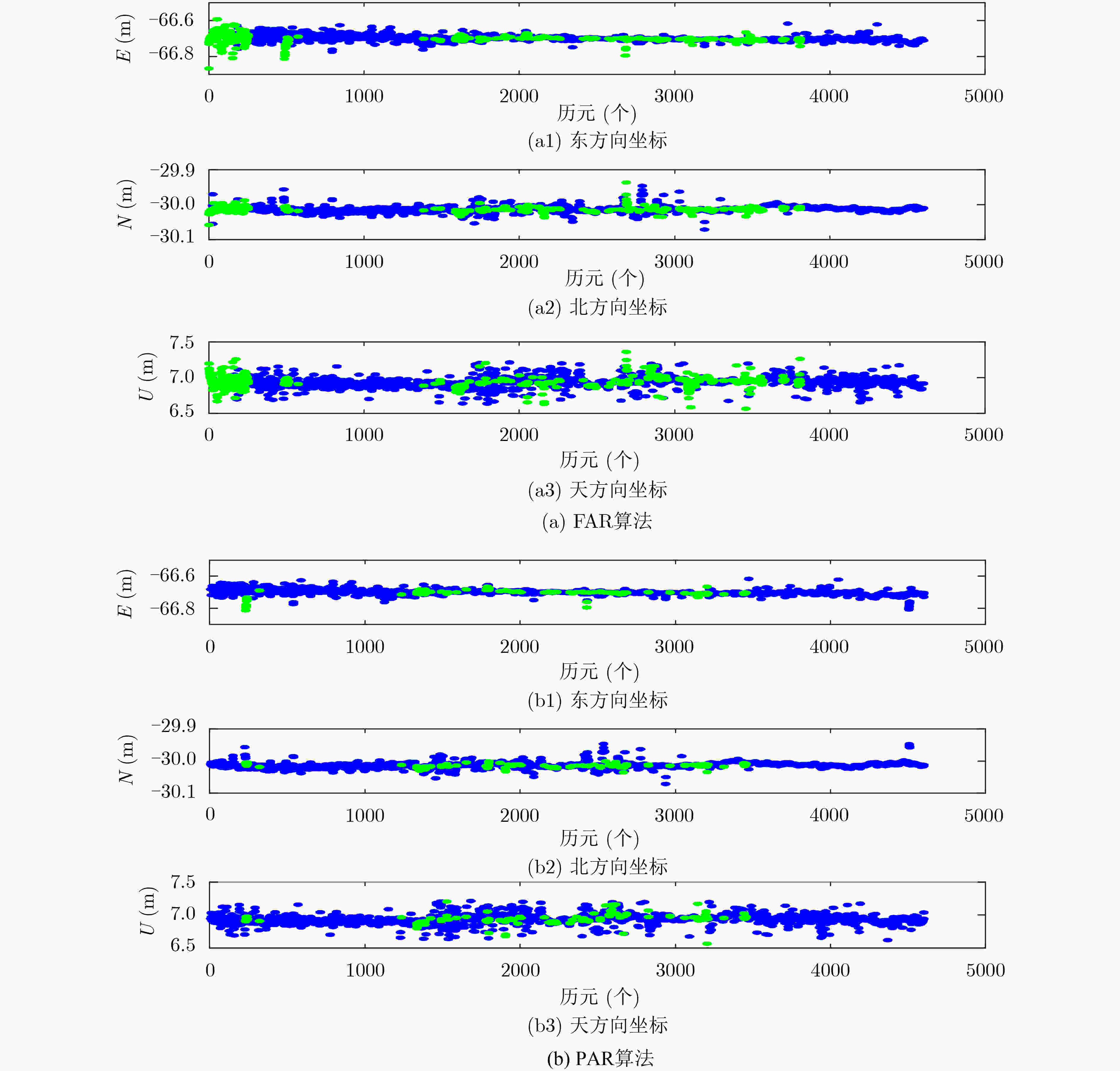
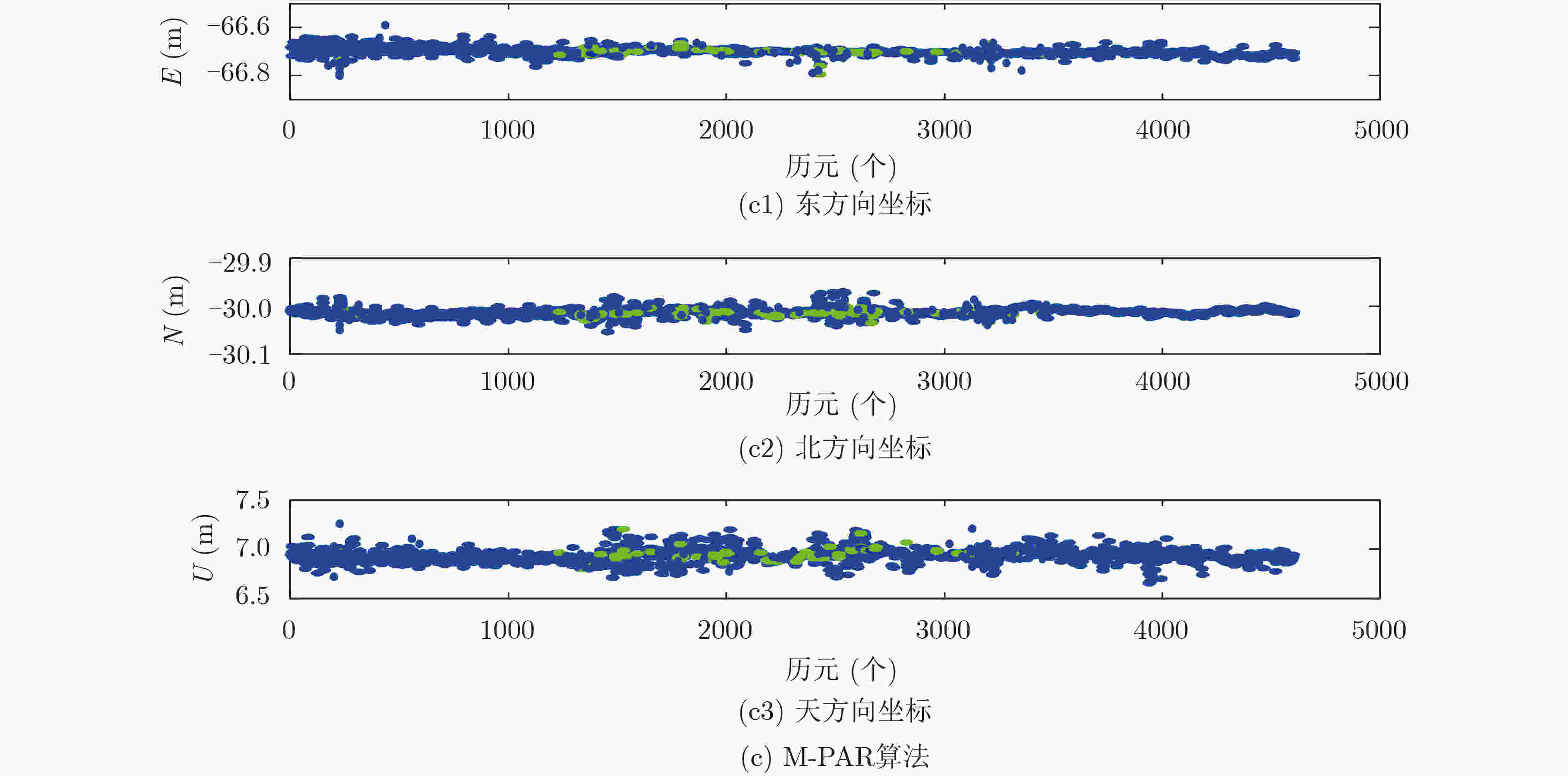
模糊度解算方法	ΔE	ΔN	ΔU
FAR(Float/fix)	0.375	0.224	0.544
PAR(Float/Fix)	0.162	0.112	0.205
M-PAR(Float/Fix)	0.045	0.068	0.104
FAR(Fix)	0.113	0.141	0.231
PAR(Fix)	0.013	0.012	0.063
M-PAR(Fix)	0.008	0.010	0.032
注：ΔE表示东向误差；ΔN表示北向误差；ΔU表示天向误差

下载: 导出CSV

参考文献(20)

[1]	TEUNISSEN P J G. Success probability of integer GPS ambiguity rounding and bootstrapping[J]. Journal of Geodesy, 1998, 72(10): 606–612. doi: 10.1007/s001900050199
[2]	范建军, 雍少为, 王飞雪. 基于卡尔曼滤波的多径误差消除及双频模糊度快速估计方法研究[J]. 电子与信息学报, 2008, 30(5): 1075–1079. FAN Jianjun, YONG Shaowei, and WANG Feixue. Study on multipath mitigation and dual-frequency fast ambiguity estimation based on Kalman filter[J]. Journal of Electronics & Information Technology, 2008, 30(5): 1075–1079.
[3]	ODIJK D, ARORA B S, and TEUNISSEN P J G. Predicting the success rate of long-baseline GPS+Galileo (Partial) ambiguity resolution[J]. The Journal of Navigation, 2014, 67(3): 385–401. doi: 10.1017/S037346331400006X
[4]	周乐韬, 黄丁发, 袁林果, 等. 网络RTK参考站间模糊度动态解算的卡尔曼滤波算法研究[J]. 测绘学报, 2007, 36(1): 37–42. doi: 10.3321/j.issn:1001-1595.2007.01.007 ZHOU Letao, HUANG Dingfa, YUAN Linguo, et al. A Kalman filtering algorithm for online integer ambiguity resolution in reference station network[J]. Acta Geodaetica et Cartographica Sinica, 2007, 36(1): 37–42. doi: 10.3321/j.issn:1001-1595.2007.01.007
[5]	丁乐乐, 张小红, 于兴旺, 等. 网络RTK双差模糊度解算成功率的提高[C]. 第二届中国卫星导航学术年会电子文集, 上海, 2011. DING Lele, ZHANG Xiaohong, YU Xingwang, et al. Network RTK double difference ambiguity resolution success rate of increase[C]. Electronic Collection of the 2nd China Satellite Navigation Annual Conference, Shanghai, China, 2011.
[6]	高旺, 高成发, 潘树国, 等. 基于部分固定策略的多系统长距离基准站间模糊度快速解算[J]. 武汉大学学报: 信息科学版, 2017, 42(4): 558–562. GAO Wang, GAO Chengfa, PAN Shuguo, et al. Fast ambiguity resolution between GPS/GLONASS/BDS combined long-range base stations based on partial-fixing strategy[J]. Geomatics and Information Science of Wuhan University, 2017, 42(4): 558–562.
[7]	BOCK Y, GOUREVITCH S A, COUNSELMAN III C C, et al. Interferometric analysis of GPS phase observations[J]. Manuscripta Geodaetica, 1986, 11(4): 282–288.
[8]	WANG Shengli, DENG Jian, OU Jikun, et al. Three-step algorithm for rapid ambiguity resolution between reference stations within network RTK[J]. The Journal of Navigation, 2016, 69(6): 1310–1324. doi: 10.1017/S037346331600031X
[9]	祝会忠, 徐爱功, 高猛, 等. BDS网络RTK中距离参考站整周模糊度单历元解算方法[J]. 测绘学报, 2016, 45(1): 50–57. ZHU Huizhong, XU Aigong, GAO Meng, et al. The algorithm of single-epoch integer ambiguity resolution between middle-range BDS network RTK reference stations[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(1): 50–57.
[10]	吴康良, 罗晨曦, 杨菂. 随机模型对BDS/GPS长基线解算精度的影响[J]. 大地测量与地球动力学, 2018, 38(4): 386–389, 406. WU Kangliang, LUO Chenxi, and YANG Di. The effect of stochastic model on the accuracy of BDS/GPS long baseline solution[J]. Journal of Geodesy and Geodynamics, 2018, 38(4): 386–389, 406.
[11]	ODIJK D, VERHAGEN S, and TEUNISSEN P J G. Medium-distance GPS Ambiguity Resolution with Controlled Failure Rate[M]. KENYON S, PACINO M C, and Marti U. Geodesy for Planet Earth. Berlin, Germany, Springer, 2012.
[12]	SASI G and RAO B. Ionospheric delay estimation for improving the global positioning system position accuracy[J]. IETE Journal of Research, 2008, 54(1): 23–29. doi: 10.1080/03772063.2008.10876178
[13]	刘鸣, 柴洪洲, 董冰全. 北斗网络RTK基准站间整周模糊度快速确定方法[J]. 信息工程大学学报, 2016, 17(6): 760–763. doi: 10.3969/j.issn.1671-0673.2016.06.023 LIU Ming, CHAI Hongzhou, and DONG Bingquan. Algorithm of instantaneous integer ambiguity resolution for reference stations of BDS network RTK[J]. Journal of Information Engineering University, 2016, 17(6): 760–763. doi: 10.3969/j.issn.1671-0673.2016.06.023
[14]	SUN R, HAN K, HU J, et al. Integrated solution for anomalous driving detection based on BeiDou/GPS/IMU measurementss[J]. Transportation Research Part C: Emerging Technologies, 2016, 69: 193–207. doi: 10.1016/j.trc.2016.06.006
[15]	张晋升, 李成钢, 何冰, 等. 区域电离层估计方法在网络RTK中的应用[J]. 导航定位学报, 2018, 6(3): 107–112. doi: 10.3969/j.issn.2095-4999.2018.03.020 ZHANG Jinsheng, LI Chenggang, HE Bing, et al. Application of regional ionospheric parameter estimation in network RTK[J]. Journal of Navigation and Positioning, 2018, 6(3): 107–112. doi: 10.3969/j.issn.2095-4999.2018.03.020
[16]	SCHAFFRIN B and BOCK Y. A unified scheme for processing GPS dual-band phase observations[J]. Bulletin Géodésique, 1988, 62(2): 142–160.
[17]	陈凯, 孙希延, 纪元法, 等. 基于载波相位差分的形变监测高精度定位算法[J]. 计算机应用, 2019, 39(4): 1234–1239. doi: 10.11772/j.issn.1001-9081.2018071454 CHEN Kai, SUN Xiyan, JI Yuanfa, et al. High-precision positioning algorithm for deformation monitoring based on carrier phase difference[J]. Journal of Computer Applications, 2019, 39(4): 1234–1239. doi: 10.11772/j.issn.1001-9081.2018071454
[18]	王守华, 陆明炽, 孙希延, 等. 基于无迹卡尔曼滤波的iBeacon/INS数据融合定位算法[J]. 电子与信息学报, 2019, 41(9): 2209–2216. doi: 10.11999/JEIT180748 WANG Shouhua, LU Mingchi, SUN Xiyan, et al. IBeacon/INS data fusion location algorithm based on unscented Kalman filter[J]. Journal of Electronics &Information Technology, 2019, 41(9): 2209–2216. doi: 10.11999/JEIT180748
[19]	王守华, 李云柯, 孙希延, 等. 基于低成本接收机的双天线测姿算法[J]. 计算机应用, 2019, 39(8): 2381–2385. doi: 10.11772/j.issn.1001-9081.2018122554 WANG Shouhua, LI Yunke, SUN Xiyan, et al. Dual-antenna attitude determination algorithm based on low-cost receiver[J]. Journal of Computer Applications, 2019, 39(8): 2381–2385. doi: 10.11772/j.issn.1001-9081.2018122554
[20]	TEUNISSEN P J G, JOOSTEN P, and TIBERIUS C. Geometry-free ambiguity success rates in case of partial fixing[C]. Proceedings of 1999 National Technical Meeting of the Institute of Navigation, San Diego, 1999.