Unconstrained Accurate Beat-to-beat Heart Rate Extraction Based on Piezoelectric Ceramics Sensor
-
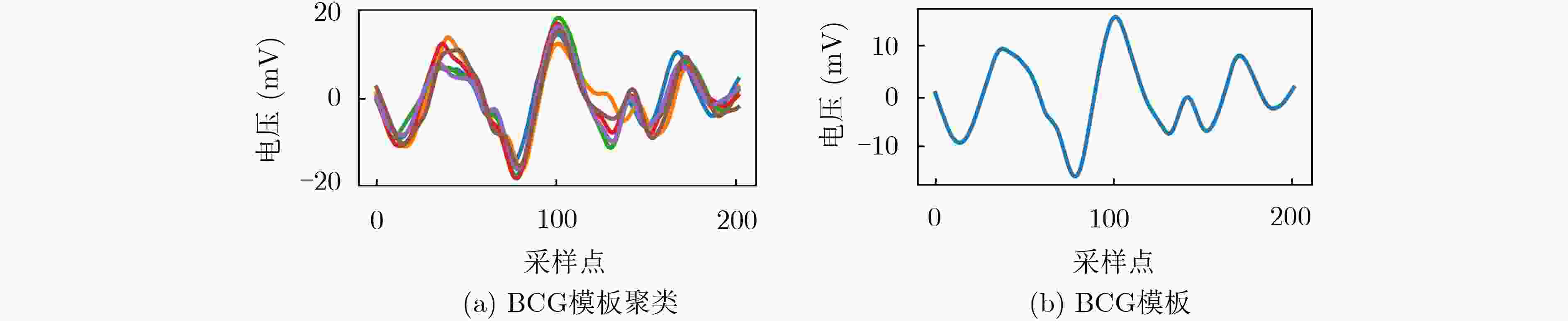
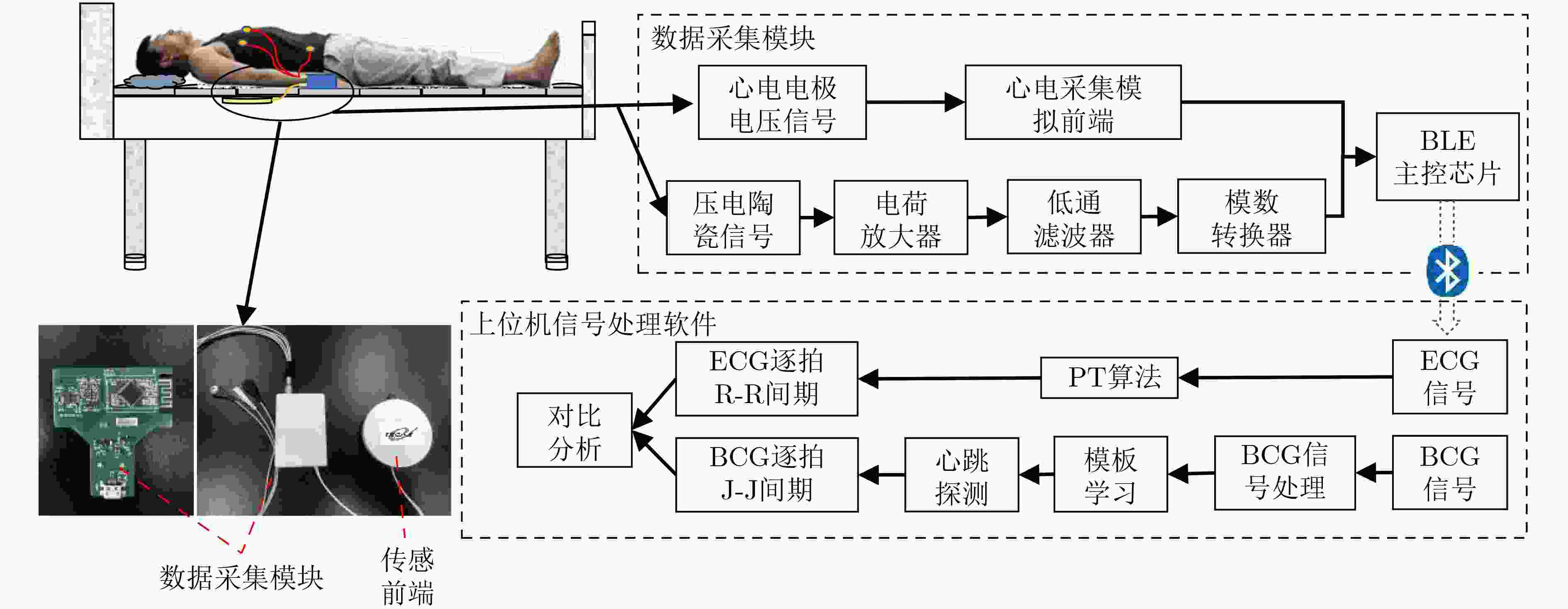
摘要: 心冲击图(BCG)可用于无接触式地监测生命体征。在BCG的逐拍心率提取中,较低的平均绝对误差对于精确地获取用户的心率变异性(HRV)指标具有重要意义。为解决目前大多数方法在逐拍心率计算精度方面的不足,该文设计了一种基于压电陶瓷的心冲击信号采集系统。通过采用合适的传感器外壳结构和采样频率,增加传感器的灵敏度和BCG的时间分辨率;通过对比不同的BCG处理方法并找到BCG中最适合提取精准逐拍心动周期的成分;同时该文提出一种采用AP聚类的自适应模板匹配算法,以准确提取心动周期信息。对15名受试者共5741次心跳数据进行分析,结果显示逐拍心动周期的平均误差为0.48%,平均绝对误差为3.78 ms,心跳覆盖率在97%以上,优于其他同类工作。Abstract: BallistoCardioGram (BCG) can be used for contactless detection of vital signs. In BCG’s beat-to-beat heart rate extraction, the lower mean absolute error is of great significance for accurately obtaining the user’s Heart Rate Variability (HRV) indicators. In order to solve the shortcomings in the accuracy of beat-to-beat heart rate calculation of most current methods, a BCG acquisition system based on piezoelectric ceramics sensor is designed in this paper. By adopting a suitable structure for the sensor‘s shell and a suitable sampling frequency, the sensitivity of the sensor and the time resolution of the BCG signal are increased. Through the analysis of BCG, the most suitable components in BCG is found to extract beat by beat cardiac cycle. At the same time, this paper proposes an adaptive template matching algorithm using AP clustering to extract accurately cardiac cycle information. Analysis of the data of 5741 heartbeats of 15 subjects shows that the average error of the beat-to-beat heartbeat cycle is 0.48%, the Mean Absolute Error (MAE) is 3.78 ms, and the heartbeat coverage is above 95%, which is better than other similar work.
-
表 1 受试者1的数据处理结果对比
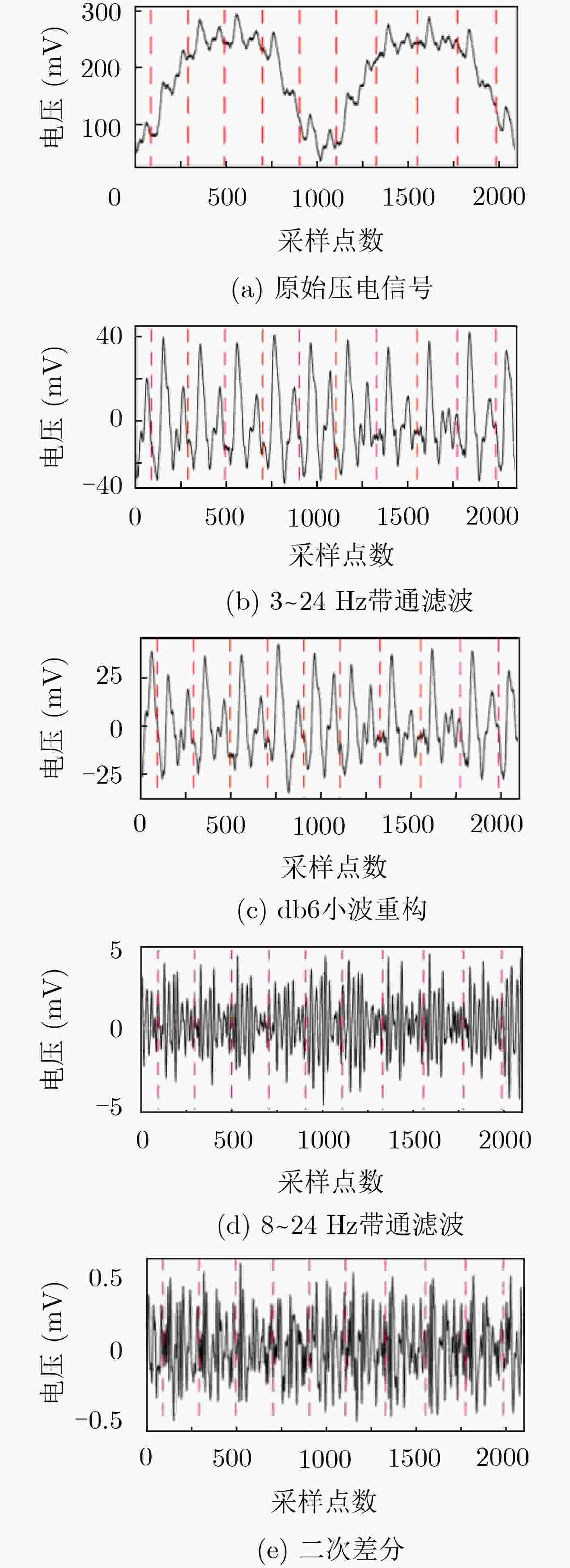
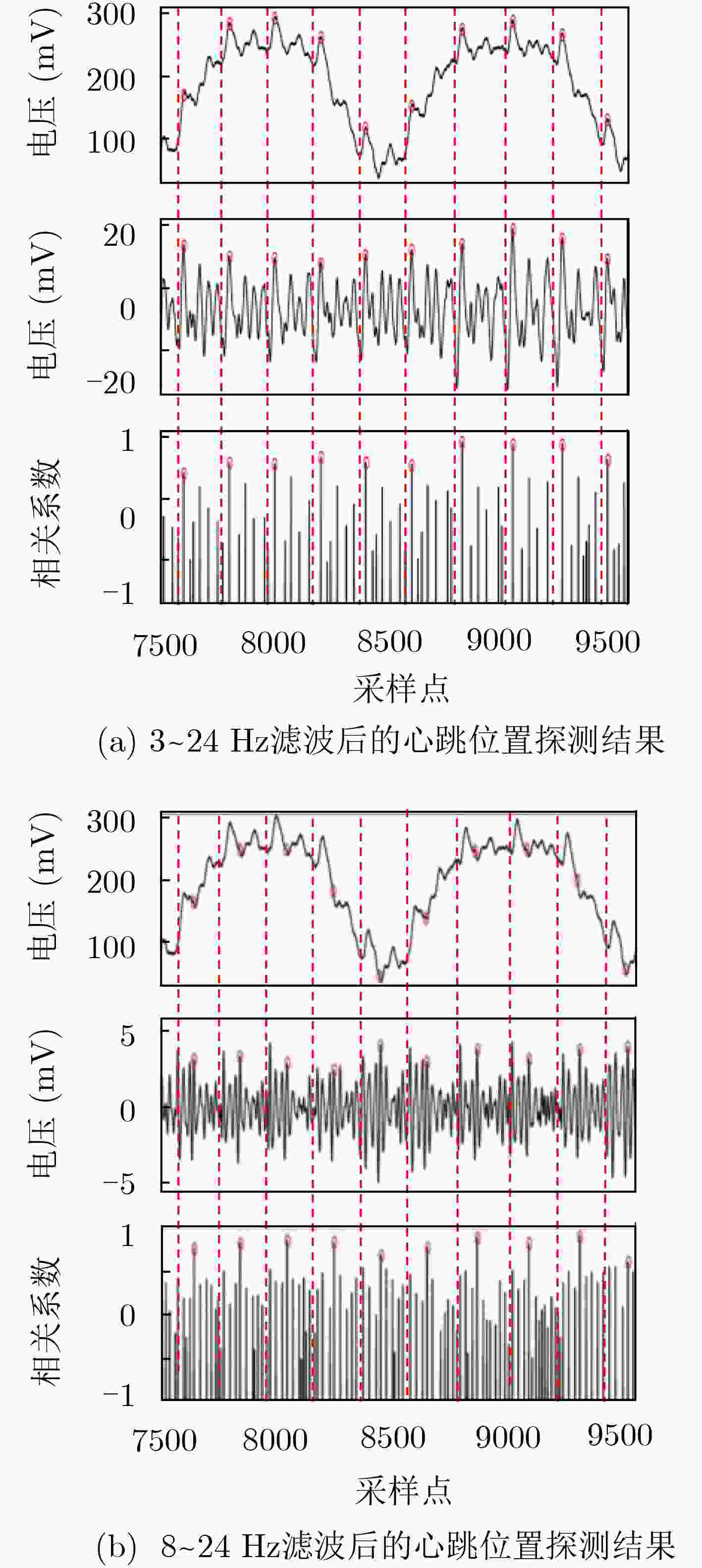
预处理方式 心跳覆盖率(%) 平均绝对误差(ms) 平均误差(%) 3~24 Hz带通滤波 100.00 14.10 1.69 db6小波重构 100.00 11.08 1.33 8~24 Hz带通滤波 98.60 3.46 0.41 二次差分 99.16 5.13 0.61 表 2 不同预处理方式下逐拍心率提取性能
受试者编号 心跳次数 3~24 Hz带通滤波 db6小波重构 8~24 Hz带通滤波 二次差分 COV(%) MAE(ms) COV(%) MAE(ms) COV(%) MAE(ms) COV(%) MAE(ms) 1 351 100.00 14.10 100.00 11.08 98.86 3.46 99.15 5.13 2 412 100.00 13.60 100.00 12.42 99.03 4.66 99.03 5.89 3 450 99.56 14.72 99.56 13.28 99.56 5.44 99.11 6.71 4 353 100.00 12.58 100.00 13.80 97.73 2.92 94.33 4.72 5 384 100.00 11.68 100.00 10.12 98.96 3.12 98.96 4.22 6 373 99.46 9.22 98.92 12.03 97.32 2.34 96.78 5.93 7 405 99.51 10.46 99.51 10.10 98.52 4.17 98.52 4.93 8 342 100.00 13.34 100.00 10.32 100.00 4.55 97.08 4.22 9 465 100.00 12.97 99.14 9.98 95.70 3.94 93.55 6.52 10 281 100.00 13.53 100.00 11.16 99.29 3.02 99.29 5.54 11 371 94.61 13.88 94.61 12.01 94.01 3.93 93.12 4.01 12 358 97.77 14.25 97.21 13.28 96.10 3.12 96.10 3.54 13 382 98.43 13.95 98.43 14.88 97.38 4.21 78.53 3.03 14 378 100.00 8.22 97.88 10.25 97.88 3.22 98.12 5.90 15 436 99.54 10.09 99.54 9.34 96.33 4.53 98.62 4.06 平均 382.7 99.26 12.44 98.99 11.60 97.78 3.78 96.02 4.96 表 3 BCG逐拍心率提取方法性能对比
作者 Bruser等人[2] Jiao等人[15] Nagura等人[16] 本文 方法 设备/采样率 床架-应变片/128 Hz 床垫下-四路液压
传感器/100 Hz床腿下-四路压力传感器/200 Hz 床垫下-压电陶瓷
传感器/250 Hz算法 形状聚类学习模板;
混合探测多示例学习 局部极大值计算模板 BCG成分分解;相关
聚类学习模板关键参数 1 Hz高通滤波;K-means
聚类特征峰数目N=7;0.4~10 Hz带通滤波学习器
参数T=M=3, β=901~8.5 Hz带通滤波;局部
最大值选取下界t=0.7 s8~24 Hz带通滤波;
AP聚类相似度s=ρ–1数据量 16×26 min 40×5 min 4×10 min 15×5 min 性能 覆盖率(%) 95.94 – 87.10 98.50 MAE(ms) 16.61 ≈30.00 9.80 3.78 平均误差(%) 1.79 4.07 ≈1.30 0.48 -
[1] JAVAID A Q, ASHOURI H, TRIDANDAPANI S, et al. Elucidating the hemodynamic origin of ballistocardiographic forces: Toward improved monitoring of cardiovascular health at home[J]. IEEE Journal of Translational Engineering in Health and Medicine, 2016, 4: 1900208. doi: 10.1109/jtehm.2016.2544752 [2] BRUSER C, STADLTHANNER K, DE WAELE S, et al. Adaptive beat-to-beat heart rate estimation in ballistocardiograms[J]. IEEE Transactions on Information Technology in Biomedicine, 2011, 15(5): 778–786. doi: 10.1109/TITB.2011.2128337 [3] SHIN J H, HWANG S H, CHANG M H, et al. Heart rate variability analysis using a ballistocardiogram during Valsalva manoeuvre and post exercise[J]. Physiological Measurement, 2011, 32(8): 1239–1264. doi: 10.1088/0967-3334/32/8/015 [4] YAO Yang, SHIN S, MOUSAVI A, et al. Unobtrusive estimation of cardiovascular parameters with limb ballistocardiography[J]. Sensors, 2019, 19(13): 2922. doi: 10.3390/s19132922 [5] SCARBOROUGH W R and TALBOT S A. Proposals for ballistocardiographic nomenclature and conventions: Revised and extended report of committee on ballistocardiographic terminology[J]. Circulation, 1956, 14(3): 435–450. doi: 10.1161/01.CIR.14.3.435 [6] JAVAID A Q, WIENS A D, FESMIRE N F, et al. Quantifying and reducing posture-dependent distortion in ballistocardiogram measurements[J]. IEEE Journal of Biomedical and Health Informatics, 2015, 19(5): 1549–1556. doi: 10.1109/JBHI.2015.2441876 [7] 崔晓雪, 成忠, 顾晔. 高血压合并糖尿病患者血压变异性与心率变异性的相关性[J]. 中国动脉硬化杂志, 2018, 26(6): 617–620. doi: 10.3969/j.issn.1007-3949.2018.06.014CUI Xiaoxue, CHENG Zhong, and GU Ye. Correlation between blood pressure variability and heart rate variability in patients with hypertension and diabetes mellitus[J]. Chinese Journal of Arteriosclerosis, 2018, 26(6): 617–620. doi: 10.3969/j.issn.1007-3949.2018.06.014 [8] MALIK J, LO Y L, and WU H T. Sleep-wake classification via quantifying heart rate variability by convolutional neural network[J]. Physiological Measurement, 2018, 39(8): 085004. doi: 10.1088/1361-6579/aad5a9 [9] KIM H G, CHEON E J, BAI D S, et al. Stress and heart rate variability: A meta-analysis and review of the literature[J]. Psychiatry Investigation, 2018, 15(3): 235–245. doi: 10.30773/pi.2017.08.17 [10] 赵荣建, 汤敏芳, 陈贤祥, 等. 基于光纤传感的生理参数监测系统研究[J]. 电子与信息学报, 2018, 40(9): 2182–2189. doi: 10.11999/JEIT170894ZHAO Rongjian, TANG Minfang, CHEN Xianxiang, et al. Research of physiological monitoring system based on optical fiber sensor[J]. Journal of Electronics and Information Technology, 2018, 40(9): 2182–2189. doi: 10.11999/JEIT170894 [11] KENRY, YEO J C, and LIM C T. Emerging flexible and wearable physical sensing platforms for healthcare and biomedical applications[J]. Microsystems & Nanoengineering, 2016, 2: 16043. doi: 10.1038/micronano.2016.43 [12] TANG Shihao, LIU Huafeng, YAN Shitao, et al. A high-sensitivity MEMS gravimeter with a large dynamic range[J]. Microsystems & Nanoengineering, 2019, 5: 45. doi: 10.1038/s41378-019-0089-7 [13] ZHAO Mingmin, YUE Shichao, KATABI D, et al. Learning sleep stages from radio signals: A conditional adversarial architecture[C]. The 34th International Conference on Machine Learning, Sydney, Australia, 2017: 4100–4109. [14] 杨昭, 杨学志, 霍亮, 等. 抗运动干扰的人脸视频心率估计[J]. 电子与信息学报, 2018, 40(6): 1345–1352. doi: 10.11999/JEIT170824YANG Zhao, YANG Xuezhi, HUO Liang, et al. Heart rate estimation from face videos against motion interference[J]. Journal of Electronics &Information Technology, 2018, 40(6): 1345–1352. doi: 10.11999/JEIT170824 [15] JIAO Changzhe, SU Boyu, LYONS P, et al. Multiple instance dictionary learning for beat-to-beat heart rate monitoring from ballistocardiograms[J]. IEEE Transactions on Biomedical Engineering, 2018, 65(11): 2634–2648. doi: 10.1109/TBME.2018.2812602 [16] NAGURA M, MITSUKURA Y, KISHIMOTO T, et al. An estimation of heart rate variability from ballistocardiogram measured with bed leg sensors[C]. 2018 IEEE International Conference on Industrial Technology (ICIT), Lyon, France, 2018: 2005–2009. doi: 10.1109/ICIT.2018.8352495. [17] 梁帆, 孟晓风, 余旸. 基于二阶伏特拉级数模型的心脏运动信号快速最小二乘估计[J]. 电子与信息学报, 2013, 35(3): 639–644. doi: 10.3724/SP.J.1146.2012.00866LIANG Fan, MENG Xiaofeng, and YU Yang. Second order volterra series model based fast least square method for heart motion prediction[J]. Journal of Electronics &Information Technology, 2013, 35(3): 639–644. doi: 10.3724/SP.J.1146.2012.00866 [18] FREY B J and DUECK D. Clustering by passing messages between data points[J]. Science, 2007, 315(5814): 972–976. doi: 10.1126/science.1136800 [19] PAN Jiapu and TOMPKINS W J. A real-time QRS detection algorithm[J]. IEEE Transactions on Biomedical Engineering, 1985, BME-32(3): 230–236. doi: 10.1109/TBME.1985.325532 -





 下载:
下载:
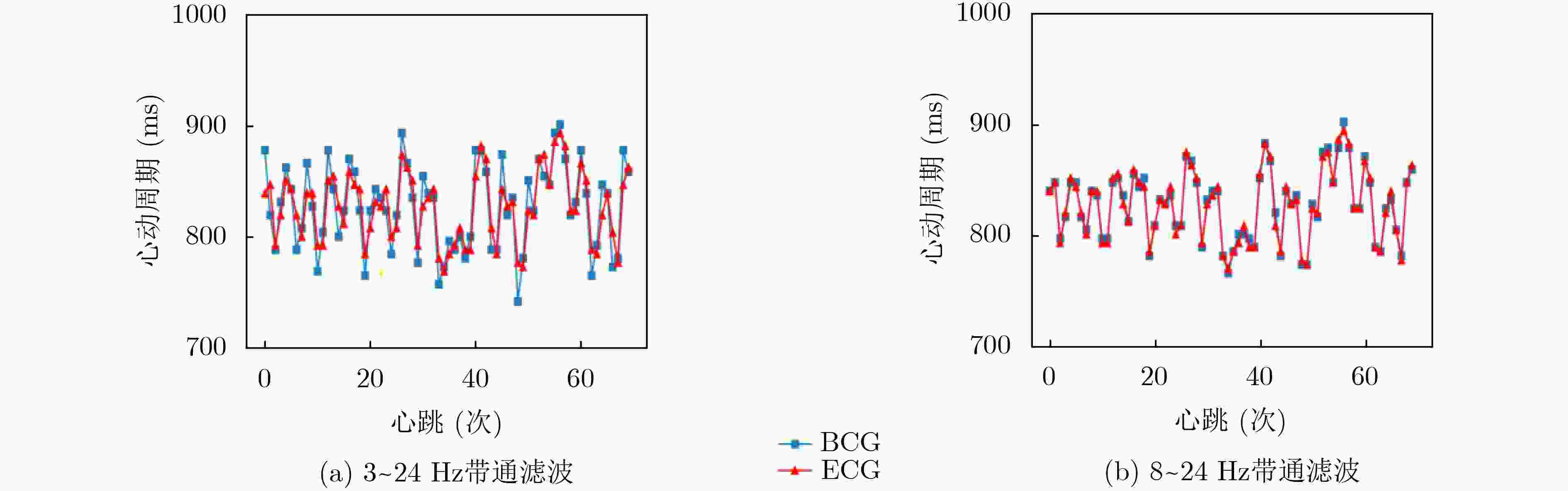
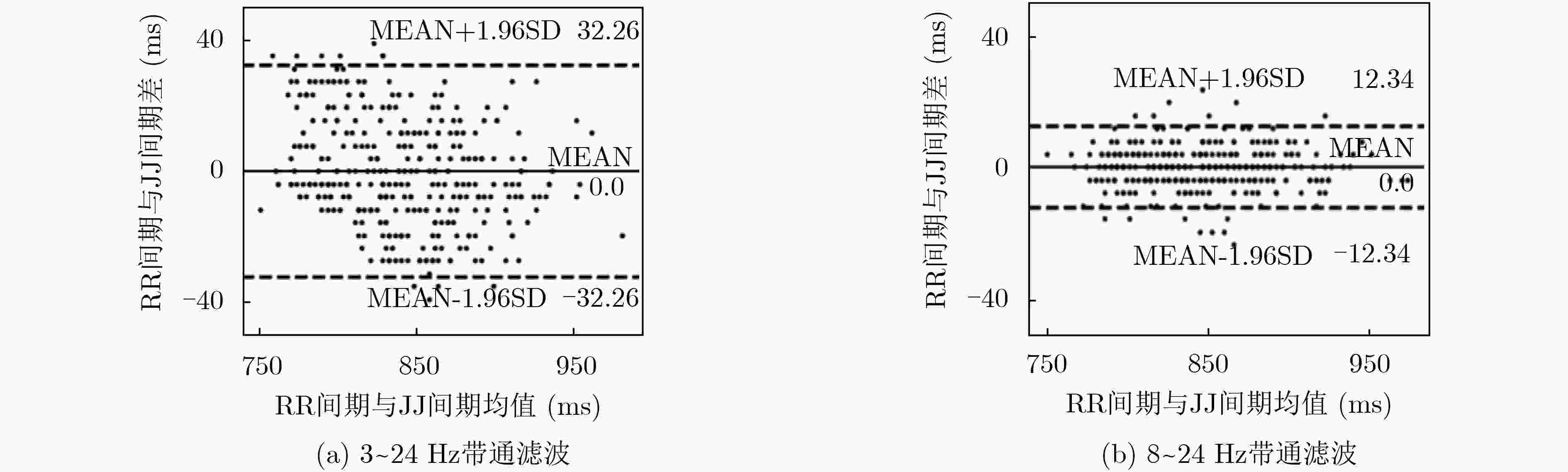
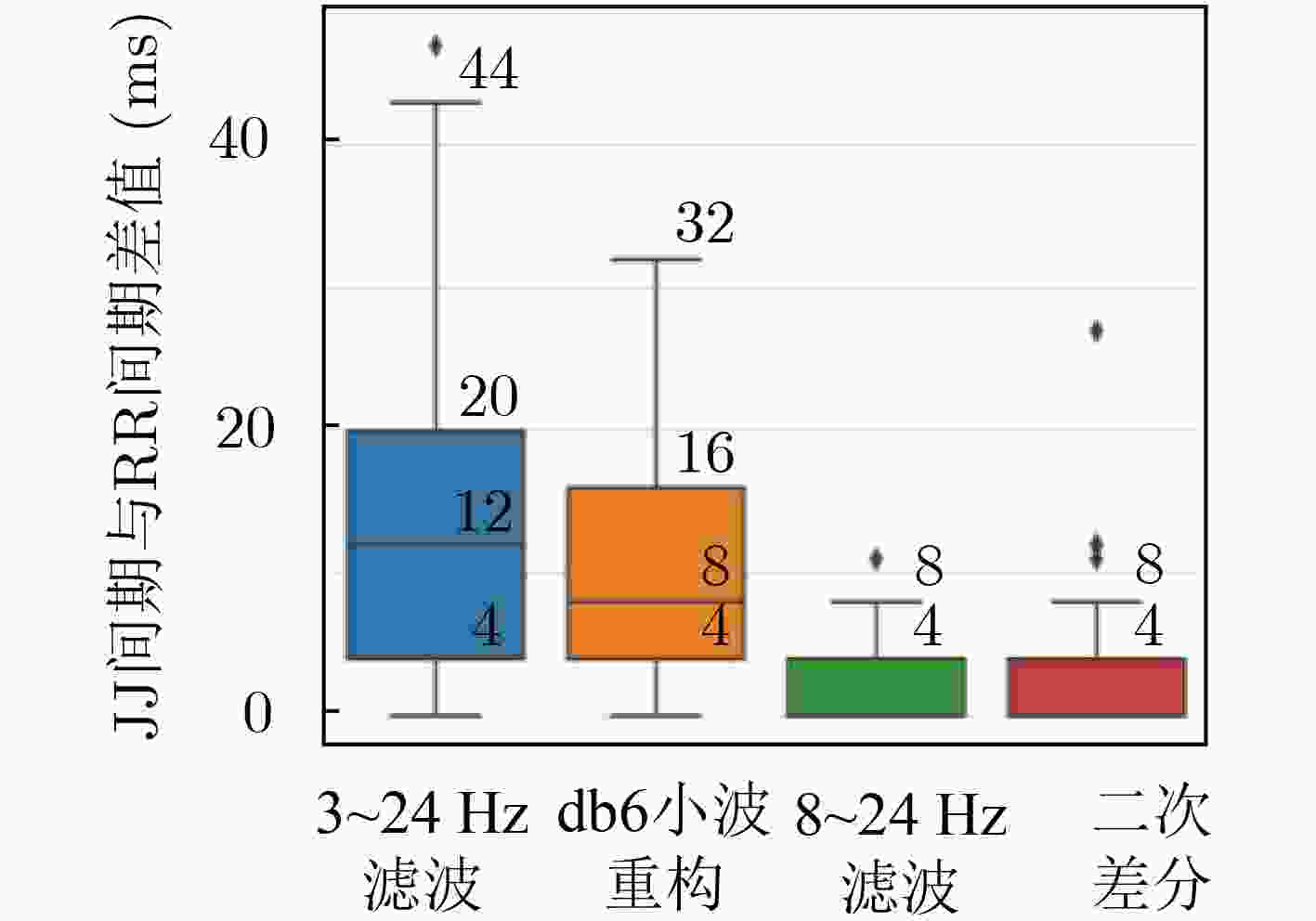


 下载:
下载:
