基于似然函数的双曲调频信号参数估计快速算法

马碧云; 元达鹏; 刘娇蛟

doi:10.11999/JEIT200044

基于似然函数的双曲调频信号参数估计快速算法

doi: 10.11999/JEIT200044

马碧云^{1, 2},
元达鹏¹,
刘娇蛟^1, ,

1.
华南理工大学电子与信息学院广州 510640
2.
自然资源部海洋环境探测技术与应用重点实验室广州 510300

基金项目: 广东省自然资源厅广东省海洋经济发展专项基金(粤自然资合[2020]009号)，国家自然科学基金(61302056，61401158)，华南理工大学中央高校基本科研业务费专项资金(2017MS047)

详细信息

作者简介:
马碧云：女，1982年生，副教授，主要研究方向为超声检测、无线携能通信研究

通讯作者:
刘娇蛟　jjliu@scut.edu.cn

中图分类号: TN911.7
计量
- 文章访问数: 1606
- HTML全文浏览量: 518
- PDF下载量: 77
- 被引次数: 0
出版历程
- 收稿日期: 2020-01-13
- 修回日期: 2020-08-01
- 网络出版日期: 2020-08-24
- 刊出日期: 2021-05-18

Fast Algorithm for Parameter Estimation of Hyperbolic Frequency Modulation Signals Based on Likelihood Function

Biyun MA^{1, 2},
Dapeng YUAN¹,
Jiaojiao LIU^{1
, ,}

1.
School of Electronic and Information Engineering, South China University of Technology, Guangzhou 510640, China
2.
Key Laboratory of Marine Environment Survey Technology and Application, Ministry of Natural Resource, Guangzhou 510300, China

Funds: The Key Program of Marine Economy Development, Department of Natural Resource of Guangdong Province under Grant (YZRZH[2020]009), The National Natural Science Foundation of China (61302056, 61401158), The Basic Research Business Expenses of Central Universities of South China University of Technology (2017MS047)

摘要

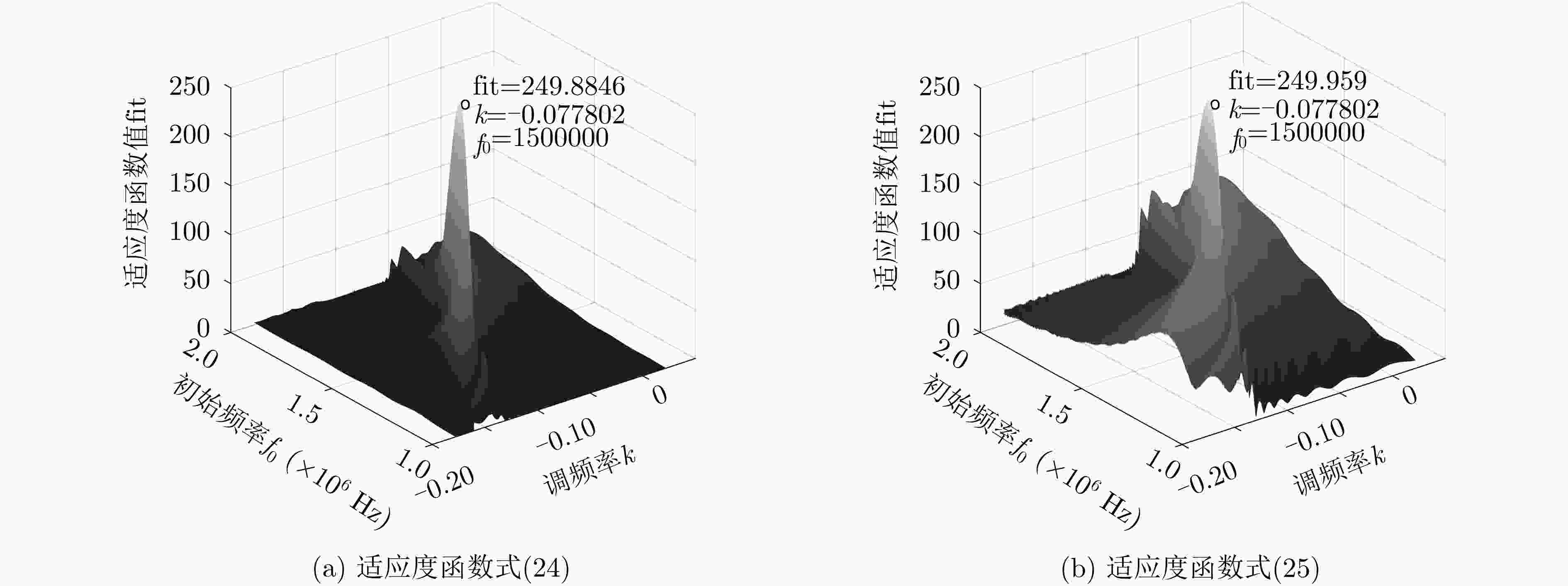
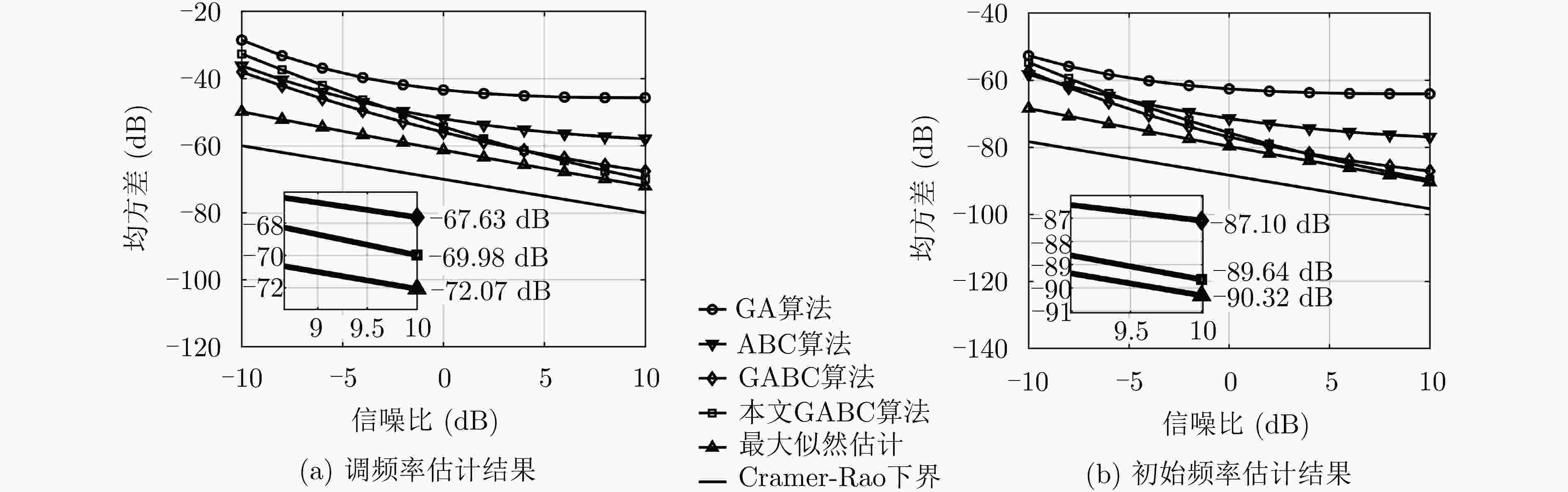
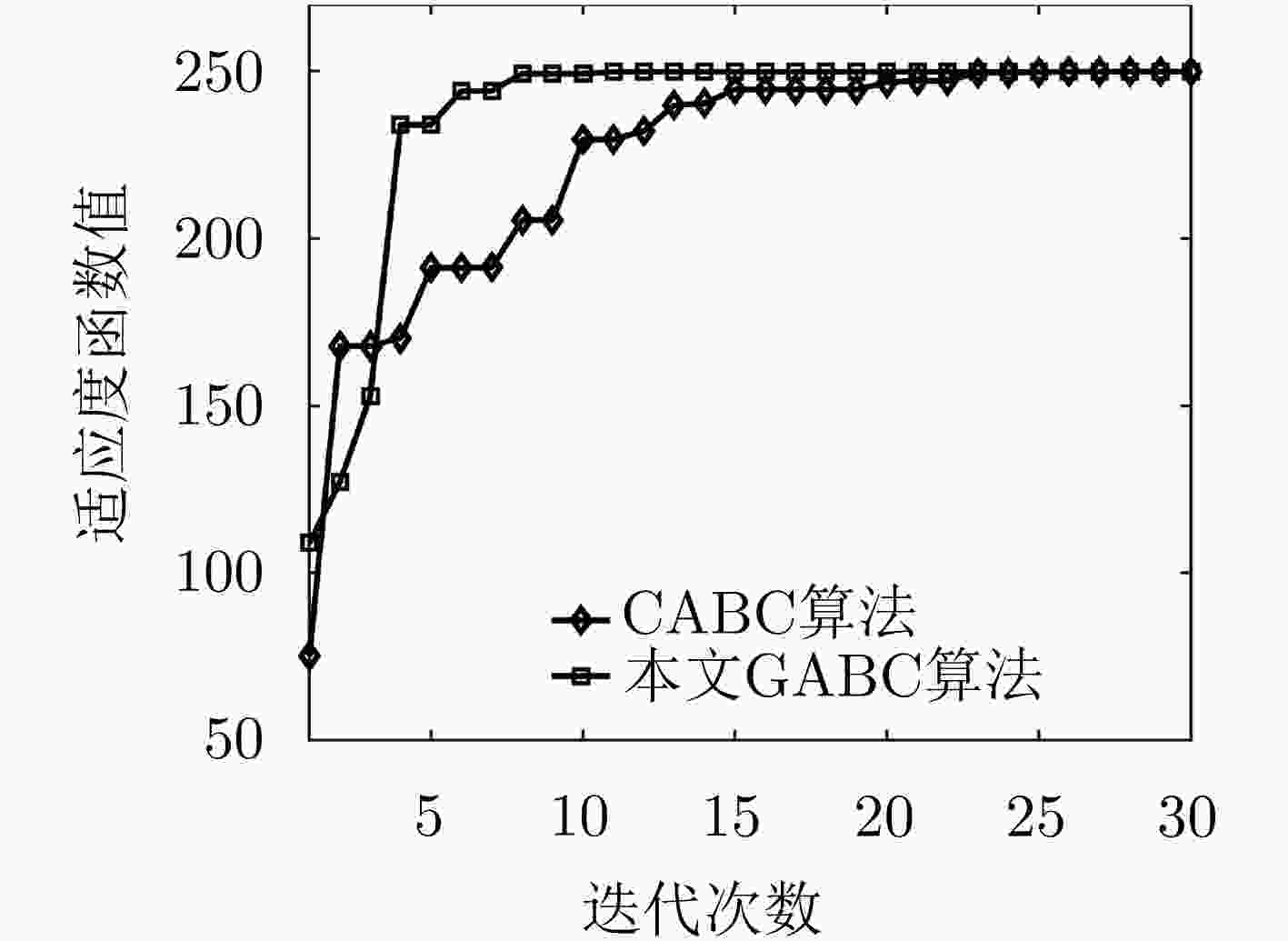
摘要: 相较于线性调频(LFM)信号，双曲调频(HFM)信号因具有良好的脉冲压缩性能和多普勒不变性，被广泛用于雷达侦查、水声探测等多普勒影响严重的场景中，其中HFM信号的参数估计问题尤为重要。有鉴于此，该文提出一种基于似然函数的HFM信号参数估计快速算法。文中首先推导出HFM信号的Cramer-Rao下界作为参数估计的性能评估标准；然后基于高斯随机噪声，构建了HFM信号的似然函数，并结合数据向量化的特点提出一种改进的适应度函数，最后利用全局最优引导人工蜂群(GABC)算法对该适应度函数进行极值寻优，从而实现HFM信号的参数估计；通过蒙特卡洛仿真证明了该方法在信噪比为3 dB以上时，HFM信号的参数估计结果的均方误差更逼近Cramer-Rao下界，且运算量约是原来的1/3，在保证估计精度的同时提高算法收敛速度。
- 信号处理 /
- 双曲调频 /
- 参数估计 /
- 似然函数
Abstract: Compared with Linear Frequency Modulation (LFM) signals, Hyperbolic Frequency Modulation (HFM) signals, which have good performance of the pulse compression and the Doppler invariance, are widely used in scenes with severe Doppler effects such as radar detection and underwater acoustic detection, and among them, the parameter estimation problem of HFM signals is particularly important. In view of this, this paper proposes a Fast Algorithm for Parameter Estimation of Hyperbolic Frequency Modulation Signals Based on Likelihood Function. Firstly, the Cramer-Rao lower bound of the HFM signal is derived as the performance evaluation standard for parameter estimation; Then based on the Gaussian random noise, the likelihood function of the HFM signal is constructed, and an improved fitness function is proposed in combination with the characteristics of data vectorization, then the Global best guided Artificial Bee Colony (GABC) algorithm is used to optimize the fitness function to realize the parameter estimation of the HFM signal. Finally, Monte Carlo simulation results show that, compared to the method before the improvement, the mean square error of the parameter estimation result of the HFM signal is closer to the Cramer-Rao lower bound when the signal-to-noise ratio is more the 3 dB, and the amount of calculation is about one-third of the method before improvement, which improves the algorithm convergence speed while ensuring the estimation accuracy.
- Signal processing /
- Hyperbolic Frequency Modulation(HFM) /
- Parameter estimation /
- Likelihood function

HTML全文

图 1 不同适应度函数的2维遍历结果

下载: 全尺寸图片幻灯片

图 2 不同方法下估计参数的均方误差与Cramer-Rao下界

下载: 全尺寸图片幻灯片

图 3 基于不同适应度函数的GABC算法收敛速度

下载: 全尺寸图片幻灯片

表 1 不同方法的时间复杂度

方法	时间复杂度
最大似然估计	$O\left( {\displaystyle\prod\nolimits_{j = 1}^D {\frac{ {\left( { {u_j} - {l_j} } \right)} }{ { {p_j} } } } } \right)$
GA算法	$O\left( {({C_{{\rm{GA}}}} - 2)({N_{{\rm{GA}}}} + 1){T_{{\rm{fit}}}}} \right)$
ABC算法	$O\left( {{C_{{\rm{ABC}}}}{N_{{\rm{ABC}}}}{T_{{\rm{fit}}}}} \right)$
GABC算法	$O\left( {{C_{{\rm{GABC}}}}{N_{{\rm{GABC}}}}{T_{{\rm{fit}}}}} \right)$

下载: 导出CSV

参考文献(14)

[1]	刘会杰, 高新海, 郭汝江. 一种低副瓣无混叠的线性调频信号时频分析方法[J]. 电子与信息学报, 2019, 41(11): 2614–2622. doi: 10.11999/JEIT181190 LIU Huijie, GAO Xinhai, and GUO Rujiang. A time-frequency analysis method for linear frequency modulation signal with low sidelobe and nonaliasing property[J]. Journal of Electronics &Information Technology, 2019, 41(11): 2614–2622. doi: 10.11999/JEIT181190
[2]	MENG Qingsong, SHAO Gaoping, and WANG Bin. Identification and parameter estimation of underwater LFM signals under ɑ -stable distribution noise[C]. The 8th International Conference on Electronics Information and Emergency Communication, Beijing, China, 2018: 190–193. doi: 10.1109/ICEIEC.2018.8473539.
[3]	周宝亮. 分布式相参雷达LFM宽带去斜参数估计方法[J]. 电子与信息学报, 2020, 42(7): 1566–1572. doi: 10.11999/JEIT190398 ZHOU Baoliang. Distributed coherent radar LFM wideband stretch parameter estimation method[J]. Journal of Electronics &Information Technology, 2020, 42(7): 1566–1572. doi: 10.11999/JEIT190398
[4]	GUO Yong and YANG Lidong. Method for parameter estimation of LFM signal and its application[J]. IET Signal Processing, 2019, 13(5): 538–543. doi: 10.1049/iet-spr.2018.5435
[5]	LIU Bing and FU Ping. Parameter estimation of LFM signal with narrowband jamming based on CS[C]. 2010 First International Conference on Pervasive Computing, Signal Processing and Applications, Harbin, China, 2010: 487–490. doi: 10.1109/PCSPA.2010.123.
[6]	YANG J and SARKAR T K. Doppler-invariant property of hyperbolic frequency modulated waveforms[J]. Microwave and Optical Technology Letters, 2006, 48(6): 1174–1179. doi: 10.1002/mop.21573
[7]	SUMAN J V and SEVENTLINE J B. Separation of HFM and NLFM signals for radar using fractional Fourier transform[C]. International Conference on Communication and Network Technologies, Sivakasi, India, 2014: 193–197. doi: 10.1109/CNT.2014.7062753.
[8]	林聪仁, 原玉婷, 孙海信, 等. 双曲调频信号的级联原子库参数估计[J]. 哈尔滨工程大学学报, 2016, 37(4): 625–628. doi: 10.11990/jheu.201501025 LIN Congren, YUAN Yuting, SUN Haixin, et al. Estimating parameters of hyperbolic modulation frequency signal based on cascade dictionary[J]. Journal of Harbin Engineering University, 2016, 37(4): 625–628. doi: 10.11990/jheu.201501025
[9]	赵砚博. 宽带水声信道参数估计及应用[D]. [博士论文], 华南理工大学, 2016. ZHAO Yanbo. Parameter estimation and applications for wideband underwater acoustic channels[D]. [Ph. D. dissertation], South China University of Technology, 2016.
[10]	KAY S M. Fundamentals of Statistical Signal Processing: Estimation Theory[M]. Upper Saddle River, USA: Prentice-Hall, Inc., 1993: 23–44.
[11]	IKRAM M Z, ABED-MERAIM K, and HUA Yingbo. Estimating the parameters of chirp signals: An iterative approach[J]. IEEE Transactions on Signal Processing, 1998, 46(12): 3436–3441. doi: 10.1109/78.735320
[12]	KARABOGA D and BASTURK B. A powerful and efficient algorithm for numerical function optimization: Artificial bee colony (ABC) algorithm[J]. Journal of Global Optimization, 2007, 39(3): 459–471. doi: 10.1007/s10898-007-9149-x
[13]	ZHU Guopu and KWONG S. Gbest-guided artificial bee colony algorithm for numerical function optimization[J]. Applied Mathematics and Computation, 2010, 217(7): 3166–3173. doi: 10.1016/j.amc.2010.08.049
[14]	王士谦. 基于群智能优化的线性调频信号参数估计[D]. [硕士论文], 吉林大学, 2019. WANG Shiqian. Parameter estimation of chirp signal based on group intelligence optimization[D]. [Master dissertation], Jilin University, 2019.