Research on NOMA-MEC-Based Offloading Strategy in Internet of Vehicles
-
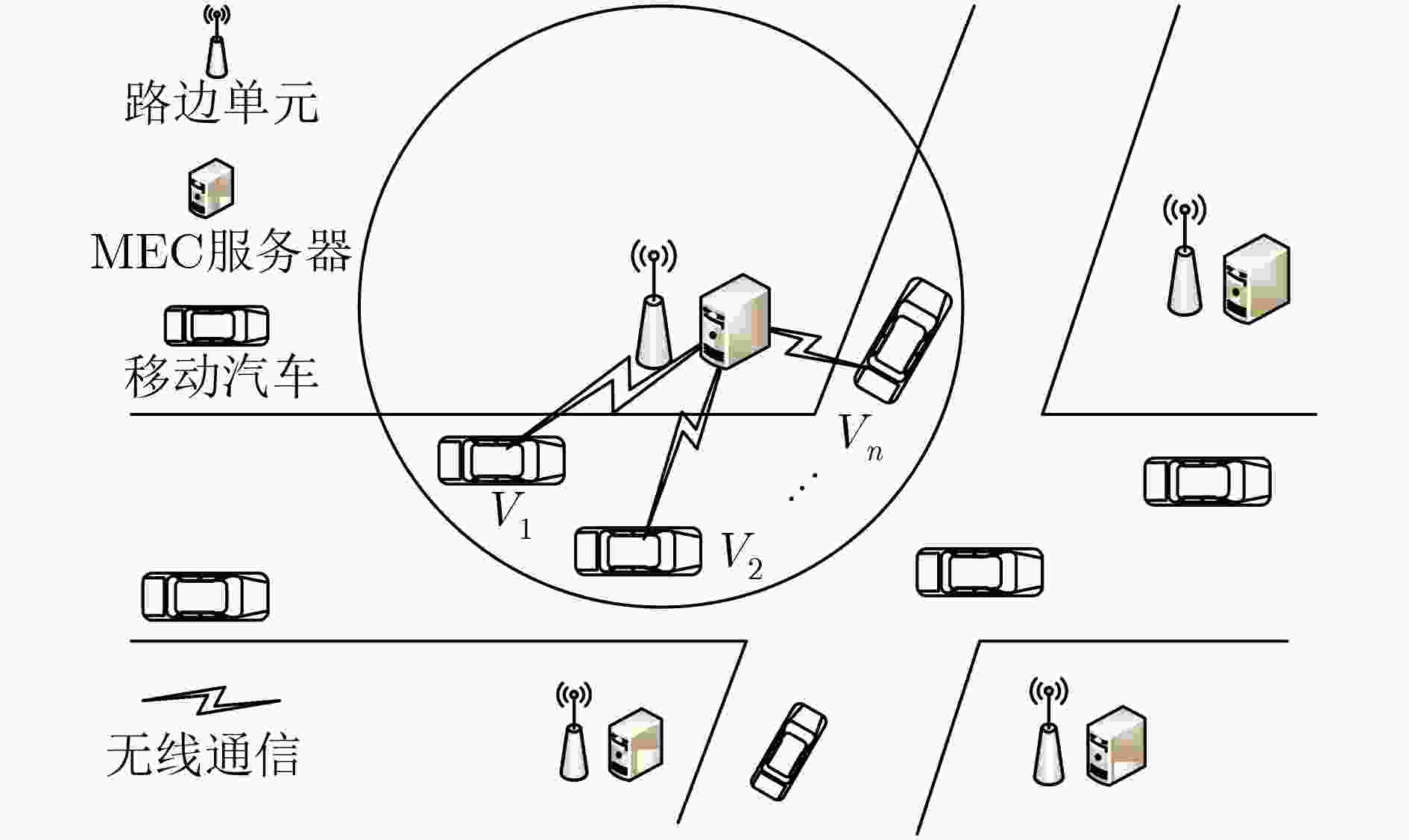
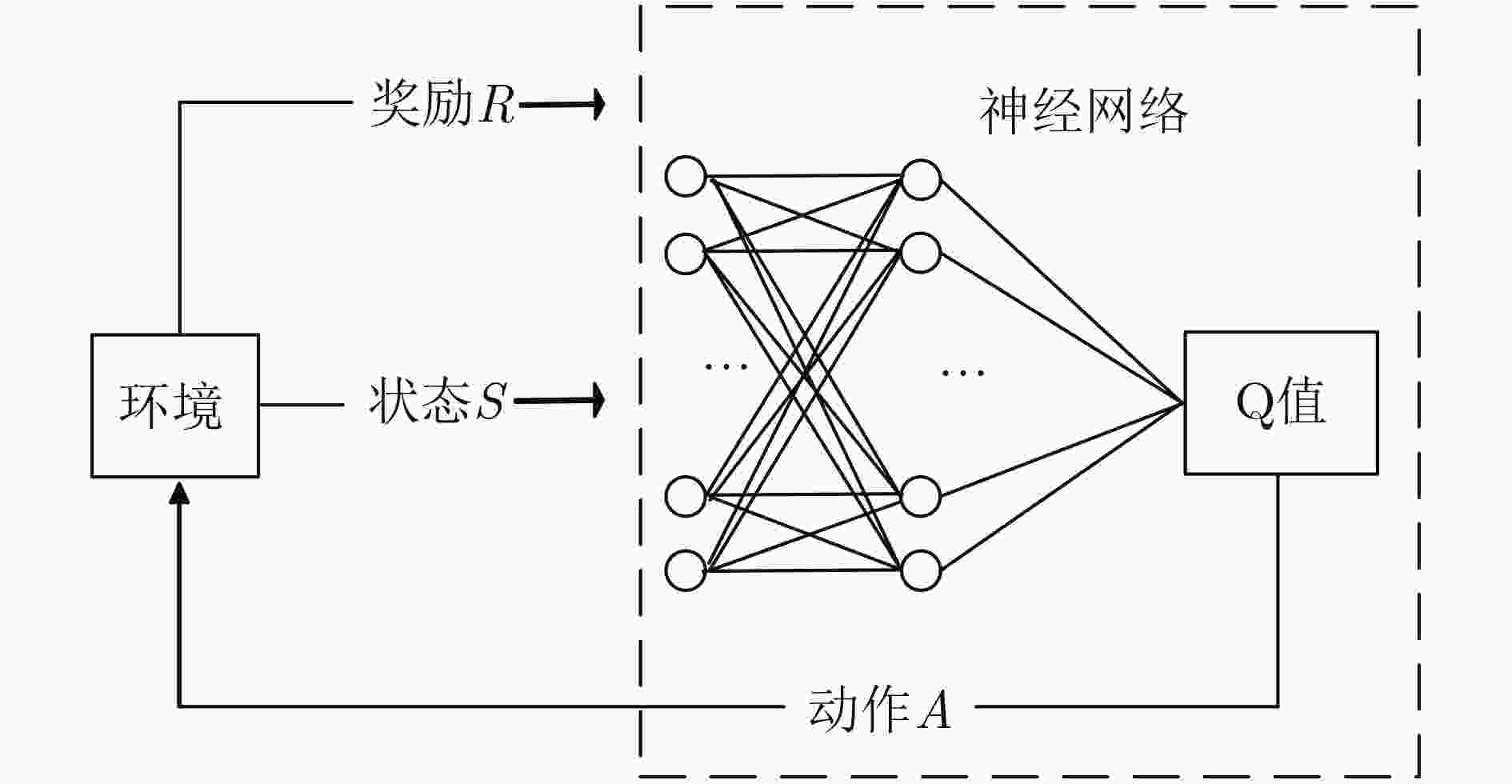
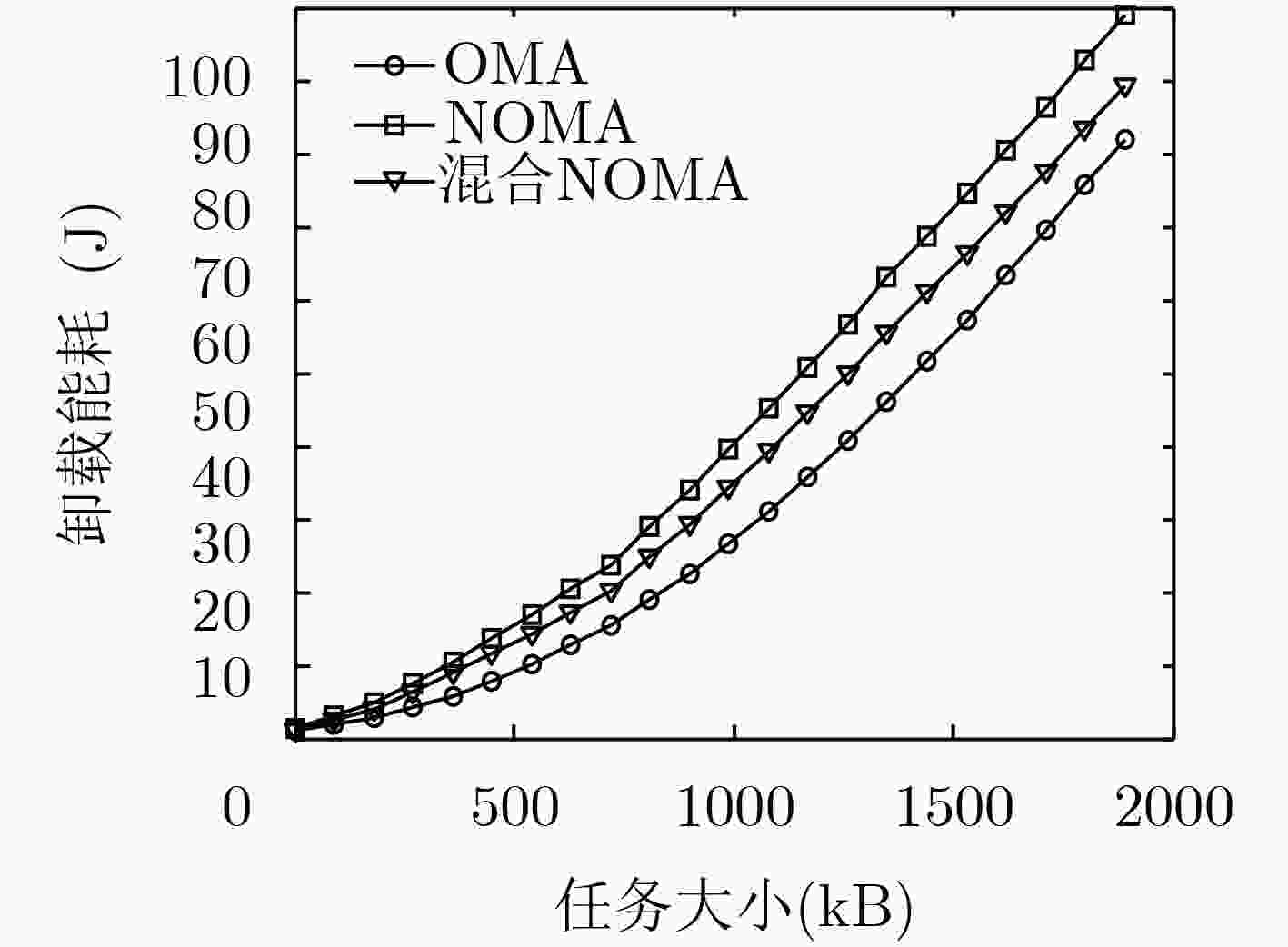
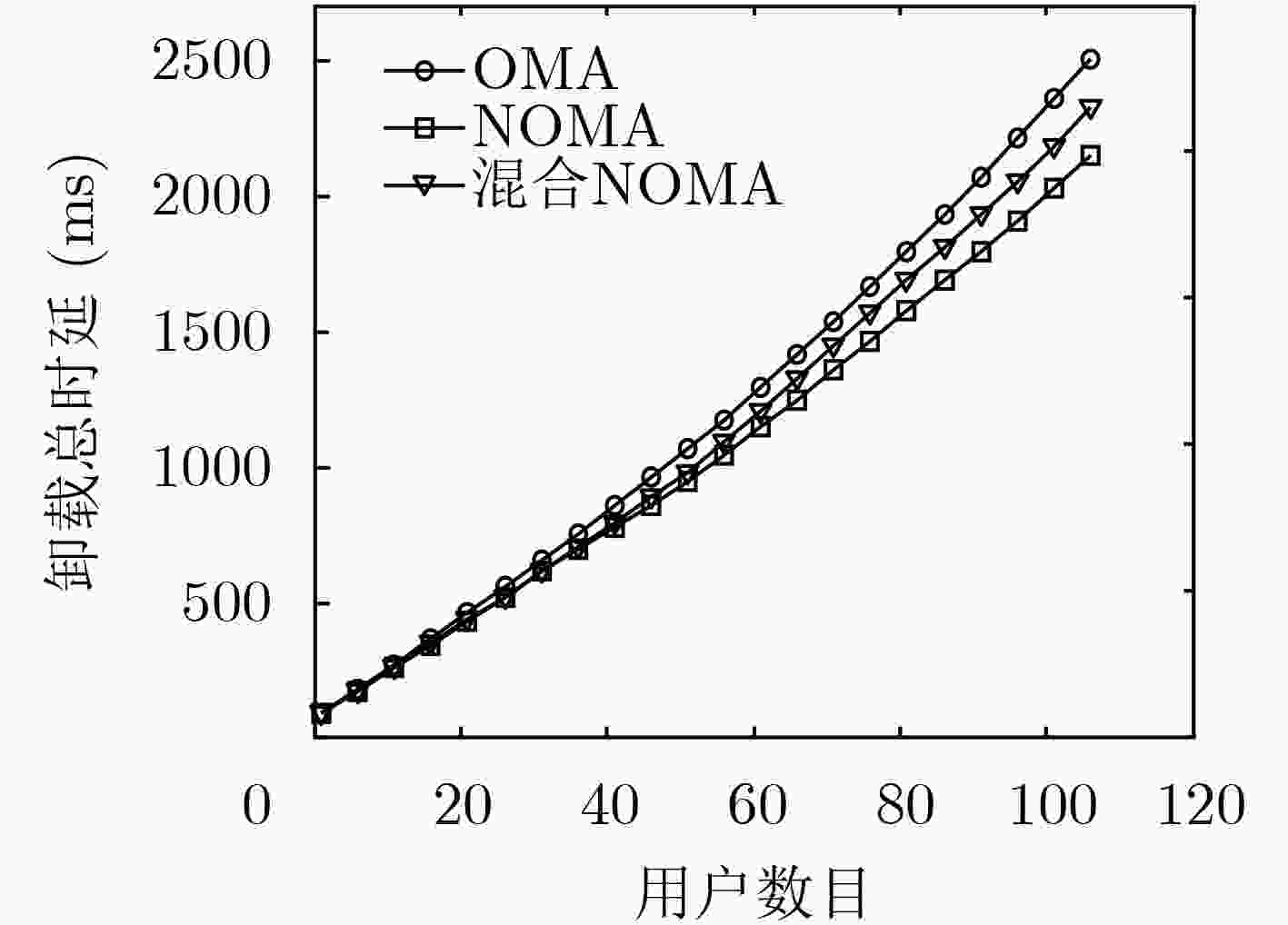
摘要: 随着车联网(IoV)的迅猛发展,请求进行任务卸载的汽车终端用户也逐渐增长,而基于移动边缘计算(MEC)的通信网络能够有效地解决任务卸载在上行传输时延较高的挑战,但是该网络模型同时也面临着信道资源不足的问题。该文引入的非正交多址(NOMA)技术相较于正交多址(OMA)能够在相同的信道资源条件下为更多的用户提供任务卸载,同时考虑到任务卸载过程中多方面的影响因子,提出了混合NOMA-MEC卸载策略。该文设计了一种基于深度学习网络(DQN)的博弈算法,帮助车辆用户进行信道选择,并通过神经网络多次迭代学习,为用户提供最优的功率分配策略。仿真结果表明,该文所提出的混合NOMA-MEC卸载策略能够有效地优化多用户卸载的时延以及能耗,最大限度保证用户效益。Abstract: With the rapid development of the Internet of Vehicles (IoV), the number of cars and users requesting tasks offloading is also increasing. The Mobile Edge Computing (MEC) can effectively solve the challenge of high offload transmission delays for task offloading in communication network, but there still is a problem that the channel resources are insufficient in the network model. Compared with traditional Orthogonal Multiple Access (OMA), the technology of Non-Orthogonal Multiple Access (NOMA) can service more users with task offload under the same channel resource conditions. In this paper, considering the multiple aspects of task offloading impact factor, a mixed unloading strategy based on NOMA-MEC is proposed. A game algorithm based on Deep Q-learning Network (DQN) is designed to make channel selection for vehicle users and provide an optimal power allocation strategy through multiple iterative learning of neural networks. The simulation results show that the proposed hybrid NOMA-MEC offloading strategy can effectively optimize the multi-user offloading delay and energy consumption and ensure maximize the benefits of users.
-
表 1 基于DQN的合作博弈算法
输入:车辆的请求卸载任务集${Q_v} = \{ {S_v},{D_v}\} $以及各用户功率,
$i \in \{ 1,2, ···, {{k} }\}$输出:最优功率分配策略 (1) 初始化:用户集合 (2) for $i = 1;i < k;i + + $ (3) 根据式(1)求出各用户时延$t = \{ {t_1},{t_2}, ···, {t_k}\}$ (4) end for (5) for $i = 1;i < k;i + + $ (6) $v = [\ ]$ (7) if ${{t(i)} } \ge {{t(n)} }$: (8) 将该用户添加至新的用户集合$v$ (9) end if (10) end for (11) 利用第1阶段在更新后的用户集合$v$求出与车辆用户$n$匹配的
信道(12) 根据第2、第3两个阶段算出奖励函数,通过多次迭代求出
最优功率分配策略(13) end 表 2 混合NOMA-MEC的卸载机制
初始化车辆用户$v$的请求卸载任务${q_v} = \{ {s_v},{d_v}\} $,信道容量Q 定义该用户的最佳能耗容忍区间$(0 - {{\rm{e}}^{\max }})$、时延能耗的权衡因
子$\lambda$(1) 根据表1的功率分配策略分别求出基于OMA, NOMA,
NOMA-MEC的能耗(2) 令$G$为优化目标函数 (3) define OMA=O, NOMA=N, NOMA–MEC=NM (4) if ${\rm{sum}}\left( {{Q_v}} \right) > = {Q_{\max }}$: (5) if ${{\rm{e}}^v} < = {{\rm{e}}^{\max }}$: (6) if $t_N^v < = t_{{\rm{NM}}}^v$ or用户成本函数$G > = \lambda t_N^vp_N^v + (1 - \lambda )t_N^v$: (7) return N (8) else: (9) return NM (10) else: (11) return NM (12) else: (13) return O 表 3 部分系统仿真参数表
部分系统仿真参数 数值 请求卸载任务数据${S_v}$ 200~2000 kB 请求卸载任务时延容忍度${D_v}$ 0.01~3 s 用户噪声功率${p_v}$ –114 dBm 任务卸载传输功率$p$ 20~25 dBm 迭代次数${I_{{\rm{dd}}} }$ 1000 传输带宽$W$ 10~20 MHz 任务传输距离${d_v}$ 50~500 m 表 4 DQN相关的参数
DQN相关参数 数值 记忆池大小(Memory pool size) 500 批大小(Batch size) 32 探索率(Exploration probability) 0.1 学习率(Learning rate) 0.001 -
MEHRABI M, YOU D, LATZKO V, et al. Device-enhanced MEC: Multi-access edge computing (MEC) aided by end device computation and caching: A survey[J]. IEEE Access, 2019, 7: 166079–166108. doi: 10.1109/ACCESS.2019.2953172 HABIBI M A, NASIMI M, HAN Bin, et al. A comprehensive survey of RAN architectures toward 5G mobile communication system[J]. IEEE Access, 2019, 7: 70371–70421. doi: 10.1109/ACCESS.2019.2919657 MAO Yuyi, ZHANG Jun, and LETAIEF K B. Dynamic computation offloading for mobile-edge computing with energy harvesting devices[J]. IEEE Journal on Selected Areas in Communications, 2016, 34(12): 3590–3605. doi: 10.1109/JSAC.2016.2611964 HU Xiaoyan, WONG K K, and YANG Kun. Wireless powered cooperation-assisted mobile edge computing[J]. IEEE Transactions on Wireless Communications, 2018, 17(4): 2375–2388. doi: 10.1109/TWC.2018.2794345 LI Yong, JIN Depeng, HUI Pan, et al. Optimal base station scheduling for device-to-device communication underlaying cellular networks[J]. IEEE Journal on Selected Areas in Communications, 2016, 34(1): 27–40. doi: 10.1109/JSAC.2015.2452415 AMEMIYA K, AKIYAMA Y, KOBAYASHI K, et al. On-site evaluation of a software cellular based MEC system with downlink slicing technology[C]. The 7th IEEE International Conference on Cloud Networking (CloudNet), Tokyo, Japan, 2018: 1–7. doi: 10.1109/CloudNet.2018.8549380. WANG Hansong, LI Xi, JI Hong, et al. Dynamic offloading scheduling scheme for MEC-enabled vehicular networks[C]. 2018 IEEE/CIC International Conference on Communications in China (ICCC Workshops), Beijing, China, 2018: 206–210. doi: 10.1109/ICCChinaW.2018.8674508. 张海霞, 李腆腆, 李东阳, 等. 基于车辆行为分析的智能车联网关键技术研究[J]. 电子与信息学报, 2020, 42(1): 36–49. doi: 10.11999/JEIT190820ZHANG Haixia, LI Tiantian, LI Dongyang, et al. Research on vehicle behavior analysis based technologies for intelligent vehicular networks[J]. Journal of Electronics &Information Technology, 2020, 42(1): 36–49. doi: 10.11999/JEIT190820 DING Zhiguo, PENG Mugen, and POOR H V. Cooperative non-orthogonal multiple access in 5G systems[J]. IEEE Communications Letters, 2015, 19(8): 1462–1465. doi: 10.1109/LCOMM.2015.2441064 GUI Guan, HUANG Hongji, SONG Yiwei, et al. Deep learning for an effective nonorthogonal multiple access scheme[J]. IEEE Transactions on Vehicular Technology, 2018, 67(9): 8440–8450. doi: 10.1109/TVT.2018.2848294 DING Zhiguo, FAN Pingzhi, and POOR H V. Impact of non-orthogonal multiple access on the offloading of mobile edge computing[J]. IEEE Transactions on Communications, 2019, 67(1): 375–390. doi: 10.1109/TCOMM.2018.2870894 DING Zhiguo, NG D W K, SCHOBER R, et al. Delay minimization for NOMA-MEC offloading[J]. IEEE Signal Processing Letters, 2018, 25(12): 1875–1879. doi: 10.1109/LSP.2018.2876019 LIU Gang, WANG Zhiqing, HU Jiewen, et al. Cooperative NOMA broadcasting/multicasting for low-latency and high-reliability 5G cellular V2X communications[J]. IEEE Internet of Things Journal, 2019, 6(5): 7828–7838. doi: 10.1109/JIOT.2019.2908415 WEI Fanbo, ZHOU Ting, XU Tianheng, et al. Modeling and analysis of two-way relay networks: A joint mechanism using NOMA and network coding[J]. IEEE Access, 2019, 7: 152679–152689. doi: 10.1109/ACCESS.2019.2948656 DING Zhiguo, XU Jie, DOBRE O, et al. Joint power and time allocation for NOMA–MEC offloading[J]. IEEE Transactions on Vehicular Technology, 2019, 68(6): 6207–6211. doi: 10.1109/TVT.2019.2907253 ZHANG Haibo, WANG Zixin, and LIU Kaijian. V2X offloading and resource allocation in SDN-assisted MEC-based vehicular networks[J]. China Communications, 2020, 17(5): 266–283. doi: 10.23919/JCC.2020.05.020 SITU Z, HO I W H, HOU Yun, et al. The feasibility of NOMA in C-V2X[C]. IEEE INFOCOM 2020 - IEEE Conference on Computer Communications Workshops (INFOCOM WKSHPS), Toronto, Canada, 2020: 562–567. doi: 10.1109/INFOCOMWKSHPS50562.2020.9163009. RABEE F A, DAVASLIOGLU K, and GITLIN R. The optimum received power levels of uplink non-orthogonal multiple access (NOMA) signals[C]. 2017 IEEE 18th Wireless and Microwave Technology Conference (WAMICON), Cocoa Beach, USA, 2017: 1–4. doi: 10.1109/WAMICON.2017.7930242. LI Shulei, DU Jianbo, ZHAI Daosen, et al. Task offloading, load balancing, and resource allocation in MEC networks[J]. IET Communications, 2020, 14(9): 1451–1458. doi: 10.1049/iet-com.2018.6122 YANG Peitong, LI Lixin, LIANG Wei, et al. Latency optimization for multi-user NOMA-MEC offloading using reinforcement learning[C]. 2019 28th Wireless and Optical Communications Conference (WOCC), Beijing, China, 2019: 1–5. doi: 10.1109/WOCC.2019.8770605. 3GPP. Study on LTE-based V2X services 14.0. 0[R]. 3GPPTR 36.885, 2016. LIU Ting, ZHU Zhaowei, GU Junrong, et al. Learn to offload in mobile edge computing[C]. 2019 IEEE Global Communications Conference (GLOBECOM), Waikoloa, USA, 2019: 1–6. doi: 10.1109/GLOBECOM38437.2019.9013853. 唐伦, 肖娇, 赵国繁, 等. 基于能效的NOMA蜂窝车联网动态资源分配算法[J]. 电子与信息学报, 2020, 42(2): 526–533. doi: 10.11999/JEIT190006TANG Lun, XIAO Jiao, ZHAO Guofan, et al. Energy efficiency based dynamic resource allocation algorithm for cellular vehicular based on non-orthogonal multiple access[J]. Journal of Electronics &Information Technology, 2020, 42(2): 526–533. doi: 10.11999/JEIT190006 ZHU Jianyue, WANG Jiaheng, HUANG Yongming, et al. Resource allocation for hybrid NOMA MEC offloading[J]. IEEE Transactions on Wireless Communications, 2020, 19(7): 4964–4977. doi: 10.1109/TWC.2020.2988532 -





 下载:
下载:


 下载:
下载:
