无线物理层密钥生成技术发展及新的挑战

黄开枝; 金梁; 陈亚军; 楼洋明; 周游; 马克明; 许晓明; 钟州; 张胜军

doi:10.11999/JEIT200002

无线物理层密钥生成技术发展及新的挑战

doi: 10.11999/JEIT200002

黄开枝^{1, 2},
金梁¹,
陈亚军¹,
楼洋明¹,
周游¹,
马克明¹,
许晓明^1, ,,
钟州¹,
张胜军¹

1.
中国人民解放军战略支援部队信息工程大学郑州 450002
2.
移动互联网安全技术国家工程实验室北京 100876

基金项目: 国家自然科学基金(61521003, 61701538, 61871404, 61801435, 61601514)，国家科技重大专项“新一代宽带无线移动通信网”(2018ZX03002002)

详细信息

作者简介:
黄开枝：女，1973年出生，教授、博士生导师，研究方向为移动通信网络及信息安全

金梁：男，1969年出生，教授、博士生导师，研究方向为移动通信网络及信息安全

许晓明：男，1988年出生，副研究员，研究方向为移动通信网络及信息安全

通讯作者:
许晓明　ee_xiaomingxu@sina.com

中图分类号: TN918; TN915.81
计量
- 文章访问数: 2198
- HTML全文浏览量: 902
- PDF下载量: 325
- 被引次数: 0
出版历程
- 收稿日期: 2020-01-02
- 修回日期: 2020-08-07
- 网络出版日期: 2020-08-21
- 刊出日期: 2020-10-13

Development of Wireless Physical Layer Key Generation Technology and New Challenges

1.
PLA Strategic Support Force Information Engineering University, Zhengzhou 450002, China
2.
National Engineering Laboratory for Mobile Network Security, Beijing 100876, China

Funds: The National Natural Science Foundation of China (61521003, 61701538,61871404, 61801435, 61601514), The National Science and Technology Major Project (2018ZX03002002)

摘要

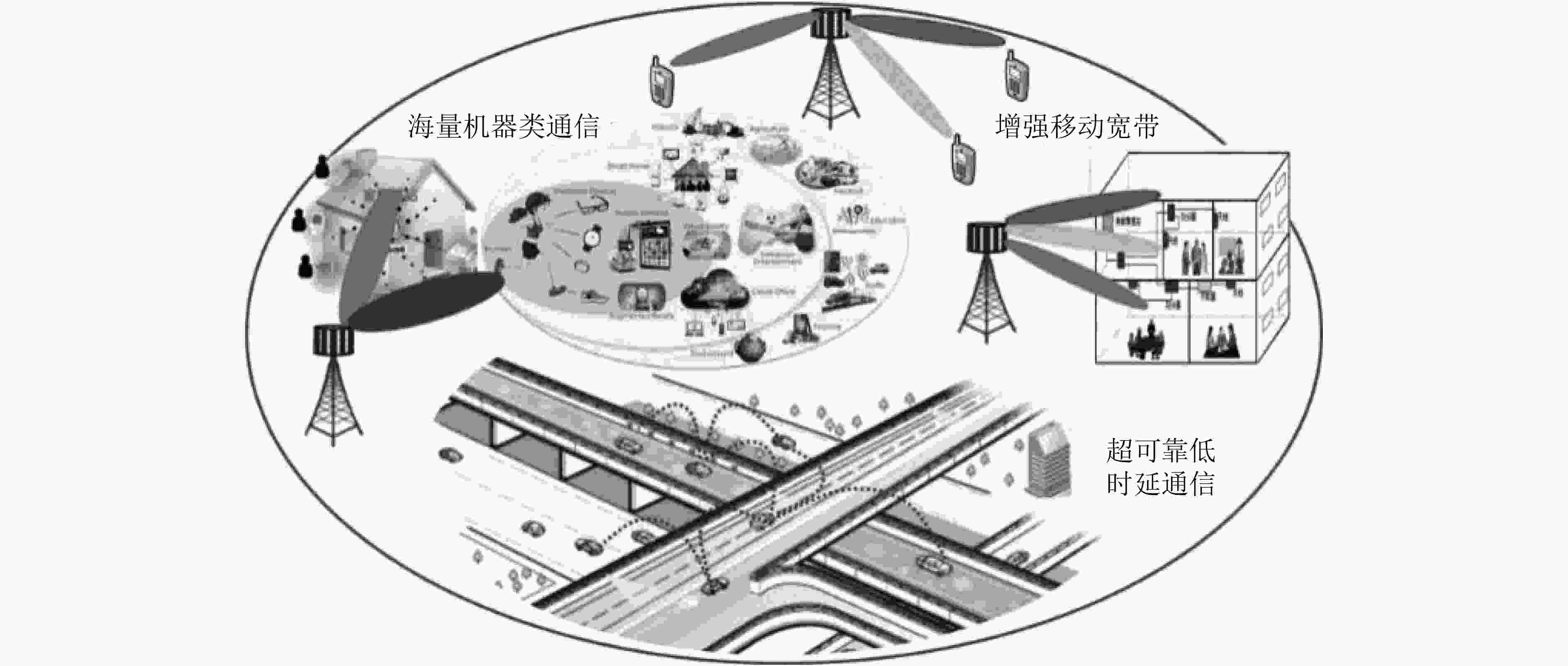
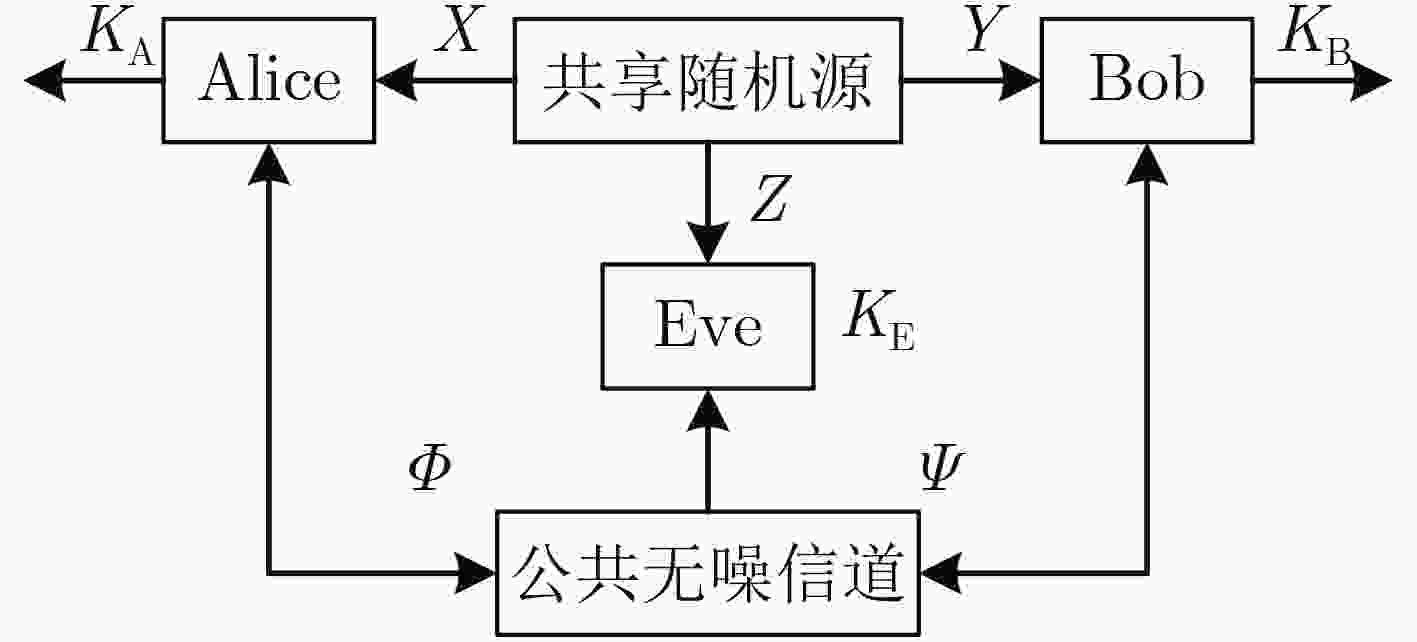
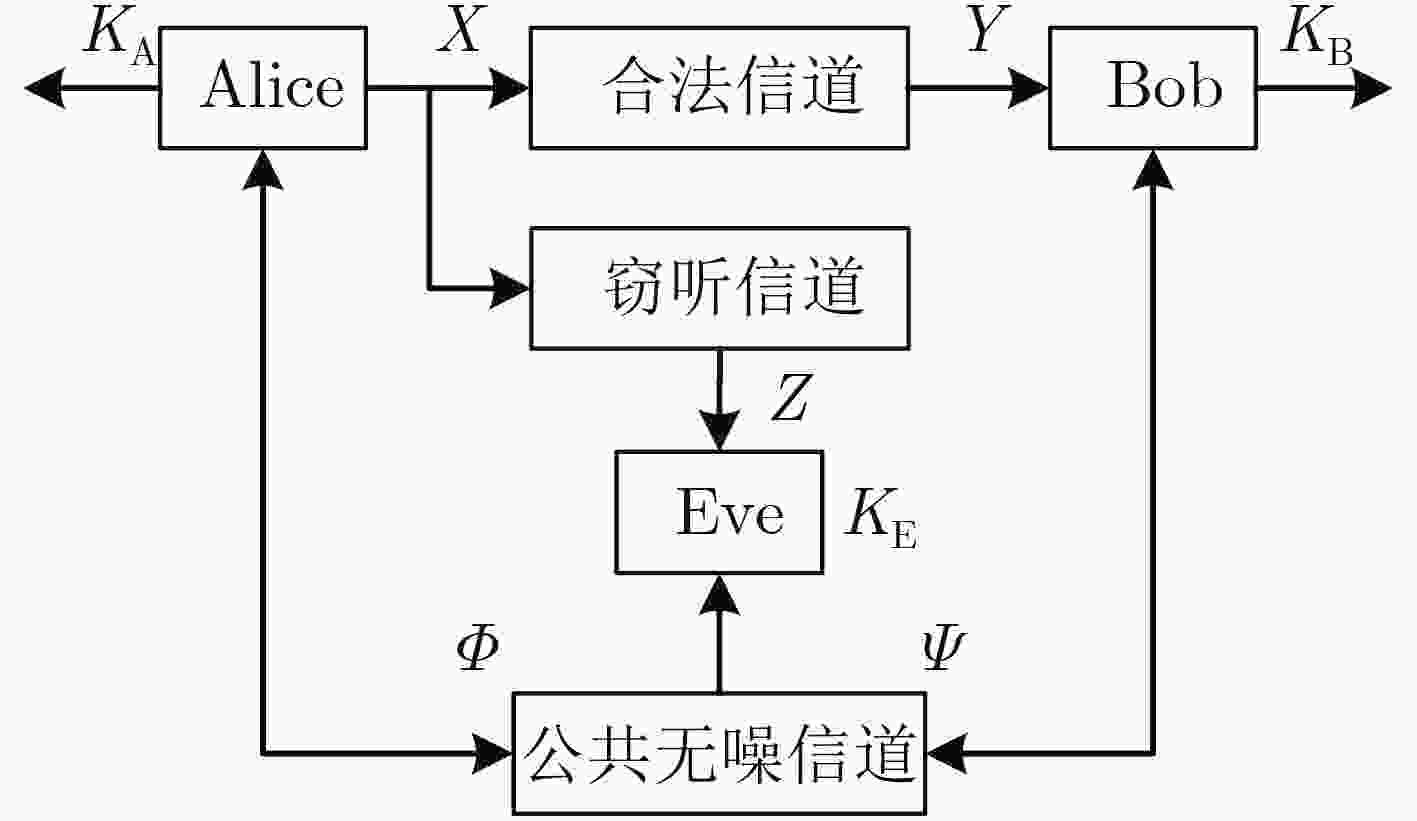
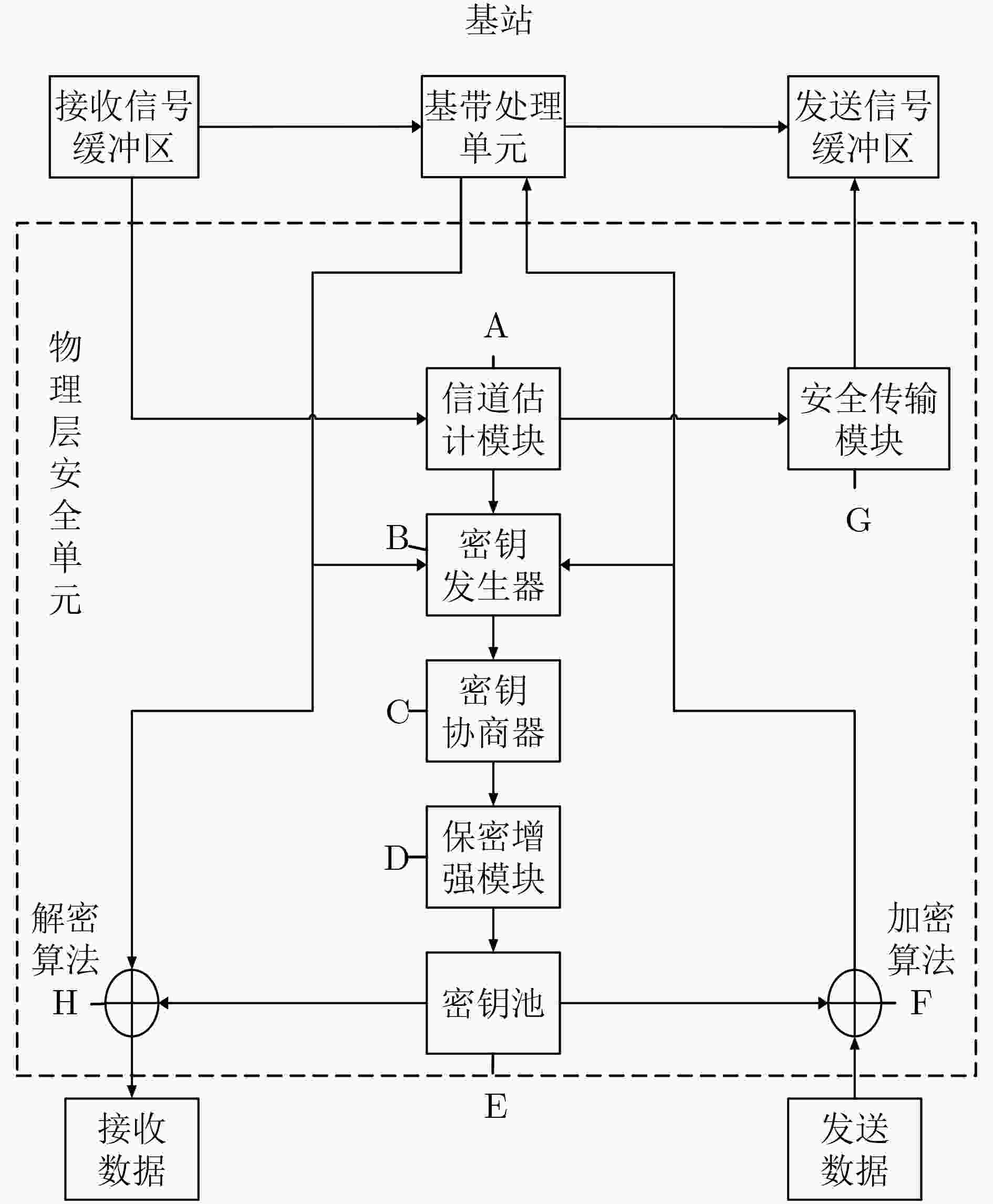
摘要: 物理层安全技术从信息论安全理论出发，保障通信安全，是实现安全与通信一体化的关键手段，逐渐成为国内外研究热点。该文围绕无线通信物理层密钥生成技术研究，主要聚焦在物理层密钥生成技术的理论模型，机制机理和研究现状，重点对比分析了两种不同类型密钥生成算法，即源型密钥生成算法和信道型密钥生成算法的区别和联系，揭示了物理层密钥技术利用通信信道内在安全属性促进通信安全的实质。特别地，该文给出了一种可行的物理层密钥生成5G工程实现框架。最后，该文展望了物理层密钥生成技术未来可能的研究方向。
- 物理层密钥生成技术 /
- 源型密钥生成算法 /
- 信道型密钥生成算法 /
- 5G工程实现框架
Abstract: Physical layer security technology secures wireless communications based on information security theory, which is the key means to realize the integration of security and communication, and has become gradually a research hotspot at home and abroad. The research of key generation technology in the physical layer of wireless communication is studied, mainly focusing on the theoretical model, mechanism and research status of key generation technologies. Through the comparison and analysis of the two different types of key generation algorithms, that is, the source key generation algorithm and the channel key generation algorithm, the essence of physical layer key technologies using communication channel’s inherent security attributes to promote communication security is revealed. In particular, a feasible physical layer key generation 5G engineering implementation framework is presented. Finally, the possible future research directions of physical layer key generation technologies is prospected.
- Physical layer key generation technology /
- Source-type key generation algorithm /
- Channel-type key generation algorithm /
- 5G engineering implementation framework

HTML全文

图 1 5G三大典型应用场景

下载: 全尺寸图片幻灯片

图 2 源型密钥生成模型

下载: 全尺寸图片幻灯片

图 3 信道型密钥生成模型

下载: 全尺寸图片幻灯片

图 4 面向集中化处理无线接入网的PLSU在基站侧的实现框图

下载: 全尺寸图片幻灯片

图 5 PLSU在终端侧的实现框图

下载: 全尺寸图片幻灯片

表 1 源型密钥生成的相关实验总结

测试环境	共享随机源	实验床	相关文献
WiFi(IEEE 802.11)	CSI,RSS	Intel5300NIC, USRP, WARP	[14,16-18]
IoT(IEEE 802.15)	RSS	MICAz^[25], TelosB^[26]	[19,27]
Bluetooth	RSS	智能手机	[20]
LTE	RSS	智能手机	[21]

下载: 导出CSV

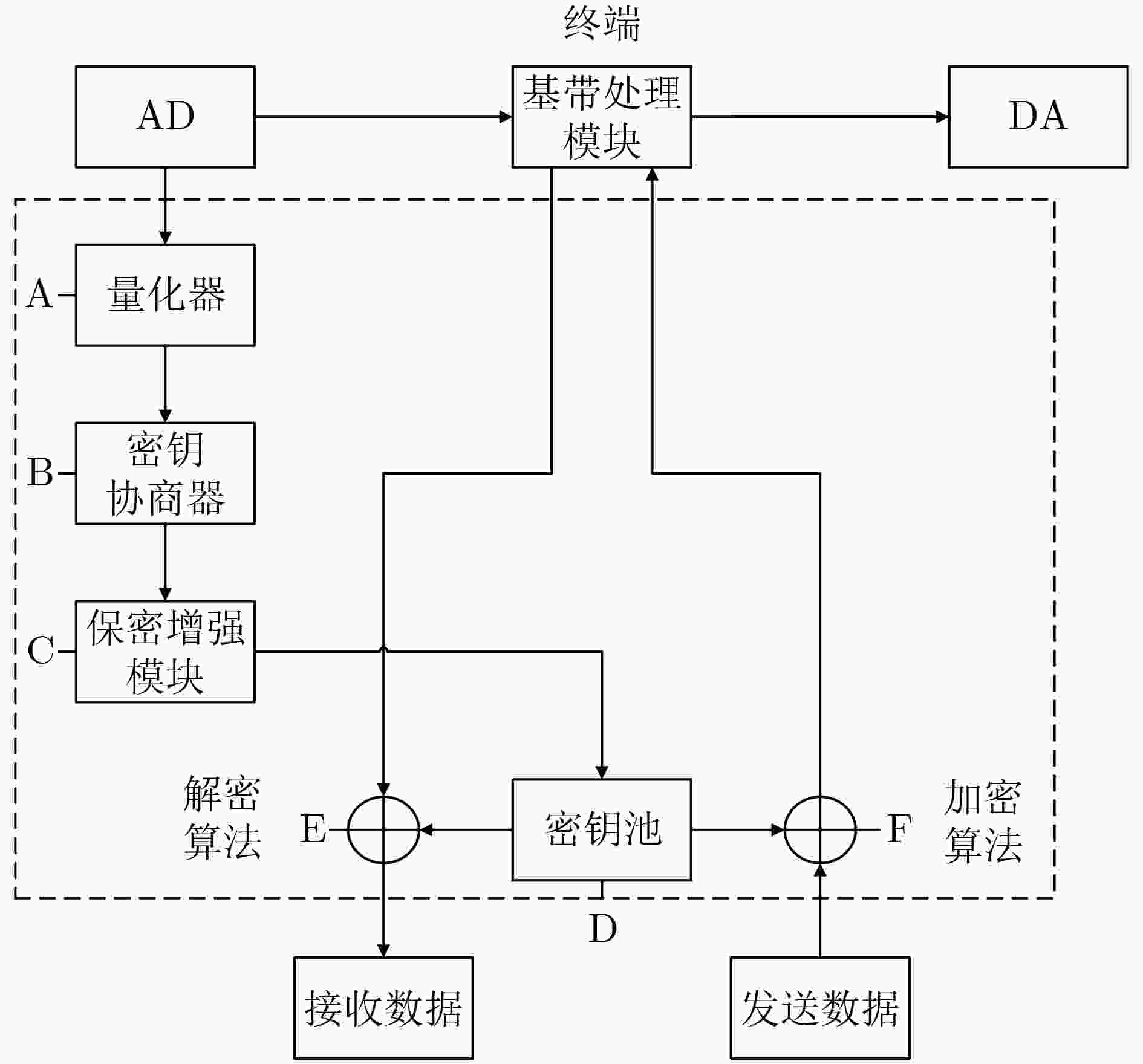
表 2 源型密钥生成步骤

步骤	功能	方法	目标
共享随机源获取	为密钥生成提供密钥源	互易信道接收信号	一致安全高效
量化	将共享随机源量化为序列	等概量化均匀量化双门限量化矢量量化	量化比特数量多量化误比特率小量化序列随机性好
信息协商	删除或纠正错误比特	Cascade方法纠错编码方法	纠错能力强协商效率高信息泄露少
隐私放大	保证密钥安全性和随机性	私密信息抽取器通用Hash函数	破解概率低于密钥强度通过NIST测试

下载: 导出CSV

参考文献(55)

史光坤. LTE/SAE系统密钥管理方案的研究与改进[D]. [博士论文], 吉林大学, 2017.

SHI Guangkun. The research and improvement of the key management schemes in LTE/SAE system[D]. [Ph. D. dissertation], Jilin University, 2017.

雷新雨. 新型公开密钥交换算法的理论与应用研究[D]. [博士论文], 重庆大学, 2015.

LEI Xinyu. Research on theory and application of new-type public key exchange algorithms[D]. [Ph. D. dissertation], Chongqing University, 2015.

GOKEY M. NSA GCHQ SIM card hack Snowden leak news[EB/OL]. https://www.digitaltrends.com/mobile/nsa-gchq-sim-card-hack-snowden-leak-news/, 2015.

5G White Paper. 5G: Rethink mobile communications for 2020+[Z]. Future Forum 5G SIG, 2014.

SHANNON C E. Communication theory of secrecy systems[J]. Bell System Technical Journal, 1949, 28(4): 656–715. doi: 10.1002/j.1538-7305.1949.tb00928.x

WYNER A D. The wire-tap channel[J]. Bell System Technical Journal, 1975, 54(8): 1355–1387. doi: 10.1002/j.1538-7305.1975.tb02040.x

ZHANG Junqing, DUONG T Q, MARSHALL A, et al. Key generation from wireless channels: A review[J]. IEEE Access, 2016, 4: 614–626. doi: 10.1109/ACCESS.2016.2521718

ZHANG Junqing, WOODS R, DUONG T Q, et al. Experimental study on key generation for physical layer security in wireless communications[J]. IEEE Access, 2016, 4: 4464–4477. doi: 10.1109/ACCESS.2016.2604618

MAURER U M. Secret key agreement by public discussion from common information[J]. IEEE Transactions on Information Theory, 1993, 39(3): 733–742. doi: 10.1109/18.256484

AHLSWEDE R and CSISZAR I. Common randomness in information theory and cryptography. I. Secret sharing[J]. IEEE Transactions on Information Theory, 1993, 39(4): 1121–1132. doi: 10.1109/18.243431

HERSHEY J E, HASSAN A A, and YARLAGADDA R. Unconventional cryptographic keying variable management[J]. IEEE Transactions on Communications, 1995, 43(1): 3–6. doi: 10.1109/26.385951

MARINO F, PAOLINI E, and CHIANI M. Secret key extraction from a UWB channel: Analysis in a real environment[C]. 2014 IEEE International Conference on Ultra-WideBand (ICUWB), Paris, France, 2014: 80–85. doi: 10.1109/ICUWB.2014.6958955.

HUANG Jingjing and JIANG Ting. Dynamic secret key generation exploiting ultra-wideband wireless channel characteristics[C]. 2015 IEEE Wireless Communications and Networking Conference (WCNC), New Orleans, USA, 2015: 1701–1706. doi: 10.1109/WCNC.2015.7127724.

LIU Hongbo, WANG Yang, YANG Jie, et al. Fast and practical secret key extraction by exploiting channel response[C]. IEEE International Conference on Computer Communications (INFOCOM), Turin, Italy, 2013: 3048–3056. doi: 10.1109/INFCOM.2013.6567117.

ZHANG Junqing, MARSHALL A, WOODS R, et al. Efficient key generation by exploiting randomness from channel responses of individual OFDM subcarriers[J]. IEEE Transactions on Communications, 2016, 64(6): 2578–2588. doi: 10.1109/TCOMM.2016.2552165

MATHUR S, TRAPPE W, MANDAYAM N, et al. Radio-telepathy: Extracting a secret key from an unauthenticated wireless channel[C]. The 14th ACM International Conference on Mobile Computing and Networking, San Francisco, USA, 2008: 128–139. doi: 10.1145/1409944.1409960.

ZENG Kai, WU D, CHAN An, et al. Exploiting multiple-antenna diversity for shared secret key generation in wireless networks[C]. 2010 Proceedings IEEE INFOCOM, San Diego, USA, 2010: 1–9. doi: 10.1109/INFCOM.2010.5462004.

WEI Yunchuan, ZENG Kai, and MOHAPATRA P. Adaptive wireless channel probing for shared key generation based on PID controller[J]. IEEE Transactions on Mobile Computing, 2013, 12(9): 1842–1852. doi: 10.1109/TMC.2012.144

HU Xiaoyan, JIN Liang, HUANG Kaizhi, et al. Physical layer secret key generation scheme based on signal propagation characteristics[J]. Acta Electronica Sinica, 2019, 47(2): 483–488. doi: 10.3969/j.issn.0372-2112.2019.02.032

PREMNATH S N, GOWDA P L, KASERA S K, et al. Secret key extraction using bluetooth wireless signal strength measurements[C]. The 11th Annual IEEE International Conference on Sensing, Communication, and Networking (SECON), Singapore, 2014: 293–301. doi: 10.1109/SAHCN.2014.6990365.

CHEN Kan, NATARAJAN B B, and SHATTIL S. Secret key generation rate with power allocation in relay-based LTE-A networks[J]. IEEE Transactions on Information Forensics and Security, 2015, 10(11): 2424–2434. doi: 10.1109/TIFS.2015.2462756

HALPERIN D, HU Wenjun, SHETH A, et al. Tool release: Gathering 802.11n traces with channel state information[J]. ACM SIGCOMM Computer Communication Review, 2011, 41(1): 53. doi: 10.1145/1925861.1925870

NI. USRP E320 (ZYNQ-7045, 2X2, 70 MHZ-6 GHZ, Board Only)–Ettus Research[EB/OL]. https://www.yottavolt.com/shop/usrp-e320-zynq-7045-2x2-70-mhz-6-ghz-board-only-ettus-research/, 2020.

Wiki. Wireless open-access research platform[EB/OL]. http://warpproject.org/trac/wiki/HardwarePlatform/, 2013.

Crossbow Technology. MICAz datasheet[EB/OL]. http://www.memsic.com/userfiles/files/Datasheets/WSN/micaz_datasheet-t.pdf, 2011.

MEMSC. TelosB datasheet[EB/OL]. http://www.willow.co.uk/TelosB_Datasheet.pdf, 2011.

WUNDER G, FRITSCHEK R, and REAZ K. RECiP: Wireless channel reciprocity restoration method for varying transmission power[C]. The 27th Annual International Symposium on Personal, Indoor, and Mobile Radio Communications (PIMRC), Valencia, Spain, 2016: 1–5. doi: 10.1109/PIMRC.2016.7794581.

LOU Yangming, JIN Liang, ZHONG Zhou, et al. Secret key generation scheme based on MIMO received signal spaces[J]. Scientia Sinica Informationis, 2017, 47(3): 362–373. doi: 10.1360/N112016-00001

TAHA H and ALSUSA E. Secret key exchange using private random precoding in MIMO FDD and TDD systems[J]. IEEE Transactions on Vehicular Technology, 2017, 66(6): 4823–4833. doi: 10.1109/TVT.2016.2611565

TAHA H and ALSUSA E. Secret key exchange under physical layer security using MIMO private random precoding in FDD systems[C]. 2016 IEEE International Conference on Communications (ICC), Kuala Lumpur, Malaysia, 2016: 1–6. doi: 10.1109/ICC.2016.7511622.

SHARIFIAN S, LIN Fuchun, and SAFAVI-NAINI R. Secret key agreement using a virtual wiretap channel[C]. IEEE Conference on Computer Communications (INFOCOM), Atlanta, USA, 2017: 1–9. doi: 10.1109/INFOCOM.2017.8057119.

KHISTI A. Secret-key agreement over non-coherent block-fading channels with public discussion[J]. IEEE Transactions on Information Theory, 2016, 62(12): 7164–7178. doi: 10.1109/TIT.2016.2618861

ZHANG Shengjun, JIN Ling, LOU Yangming, et al. Secret key generation based on two-way randomness for TDD-SISO system[J]. China Communications, 2018, 15(7): 202–216. doi: 10.1109/CC.2018.8424614

WU Feilong, WANG Wenjie, WANG Huiming, et al. A unified mathematical model for spatial scrambling based secure wireless communication and its wiretap method[J]. Scientia Sinica Informationis, 2012, 42(4): 483–492. doi: 10.1360/112011-942

HARRISON W K, ALMEIDA J, BLOCH M R, et al. Coding for secrecy: An overview of error-control coding techniques for physical-layer security[J]. IEEE Signal Processing Magazine, 2013, 30(5): 41–50. doi: 10.1109/MSP.2013.2265141

NEGI R and GOEL S. Secret communication using artificial noise[C]. VTC-2005-Fall. The 62nd IEEE Vehicular Technology Conference, 2005, Dallas, USA, 2005: 1906–1910. doi: 10.1109/VETECF.2005.1558439.

GOEL S and NEGI R. Guaranteeing secrecy using artificial noise[J]. IEEE Transactions on Wireless Communications, 2008, 7(6): 2180–2189. doi: 10.1109/TWC.2008.060848

LI Xiaohua, HWU J, and RATAZZI E P. Array redundancy and diversity for wireless transmissions with low probability of interception[C]. 2006 IEEE International Conference on Acoustics Speech and Signal Processing Proceedings, Toulouse, France, 2006: 211–221. doi: 10.1109/ICASSP.2006.1661021.

LI Xiaohua, HWU J, and RATAZZI E. Using antenna array redundancy and channel diversity for secure wireless transmissions[J]. Journal of Communications, 2007, 2(3): 24–32. doi: 10.4304/jcm.2.3.24-32

FOUNTZOULAS Y, KOSTA A, and KARYSTINOS G N. Polar-code-based security on the BSC-modeled HARQ in fading[C]. The 23rd International Conference on Telecommunications (ICT), Thessaloniki, Greece, 2016: 1–5. doi: 10.1109/ICT.2016.7500449.

ZHANG Yingxian, YANG Zhen, LIU Aijun, et al. Secure transmission over the wiretap channel using polar codes and artificial noise[J]. IET Communications, 2017, 11(3): 377–384. doi: 10.1049/iet-com.2016.0429

BAI Huiqing, JIN Liang, and YI Ming. Artificial noise aided polar codes for physical layer security[J]. China Communications, 2017, 14(12): 15–24. doi: 10.1109/cc.2017.8246334

TOPAL O A, KURT G K, and ÖZBEK B. Key error rates in physical layer key generation: Theoretical analysis and measurement-based verification[J]. IEEE Wireless Communications Letters, 2017, 6(6): 766–769. doi: 10.1109/LWC.2017.2740290

ZHANG Junqing, RAJENDRAN S, SUN Zhi, et al. Physical layer security for the internet of things: Authentication and key generation[J]. IEEE Wireless Communications, 2019, 26(5): 92–98. doi: 10.1109/MWC.2019.1800455

JIN Henglei, HUANG Kaizhi, XIAO Shuaifang, et al. A two-layer secure quantization algorithm for secret key generation with correlated eavesdropping channel[J]. IEEE Access, 2019, 7: 26480–26487. doi: 10.1109/access.2019.2893594

JIAO Long, WANG Ning, WANG Pu, et al. Physical layer key generation in 5G wireless networks[J]. IEEE Wireless Communications, 2019, 26(5): 48–54. doi: 10.1109/MWC.001.1900061

ZENG Kai. Physical layer key generation in wireless networks: Challenges and opportunities[J]. IEEE Communications Magazine, 2015, 53(6): 33–39. doi: 10.1109/MCOM.2015.7120014

JIN Liang, ZHANG Shengjun, LOU Yangming, et al. Secret key generation with cross multiplication of two-way random signals[J]. IEEE Access, 2019, 7: 113065–113080. doi: 10.1109/access.2019.2935206

LI Guyue, SUN Chen, ZHANG Junqing, et al. Physical layer key generation in 5G and beyond wireless communications: Challenges and opportunities[J]. Entropy, 2019, 21(5): 497. doi: 10.3390/e21050497

CHEN Xuxing, HE Zunwen, ZHANG Yan, et al. A key generation scheme for wireless communication based on channel characteristics[J]. Journal of Terahertz Science and Electronic Information Technology, 2017, 15(5): 834–840. doi: 10.11805/TKYDA201705.0834

QIN Dongrun and DING Zhi. Exploiting multi-antenna non-reciprocal channels for shared secret key generation[J]. IEEE Transactions on Information Forensics and Security, 2016, 11(12): 2693–2705. doi: 10.1109/TIFS.2016.2594143

LI Guyue, HU Aiqun, SUN Chen, et al. Constructing reciprocal channel coefficients for secret key generation in FDD systems[J]. IEEE Communications Letters, 2018, 22(12): 2487–2490. doi: 10.1109/LCOMM.2018.2875708

LI Shanshan, CHENG Mengfan, DENG Lei, et al. Secure key distribution strategy in OFDM-PON by utilizing the redundancy of training symbol and digital chaos technique[J]. IEEE Photonics Journal, 2018, 10(2): 7201108. doi: 10.1109/jphot.2018.2815001

ZHAO Jun. A survey of reconfigurable intelligent surfaces: Towards 6G wireless communication networks with massive MIMO 2.0[J]. arXiv, 2019, 1907.04789v1.

DI RENZO M, DEBBAH M, PHAN-HUY D T, et al. Smart radio environments empowered by reconfigurable AI meta-surfaces: An idea whose time has come[J]. EURASIP Journal on Wireless Communications and Networking, 2019, 2019(1): 129. doi: 10.1186/s13638-019-1438-9

施引文献

资源附件(0)

访问统计