A Robust Heterogeneous Clutter Suppression Method for Airborne Planar Array Radar
-
摘要:
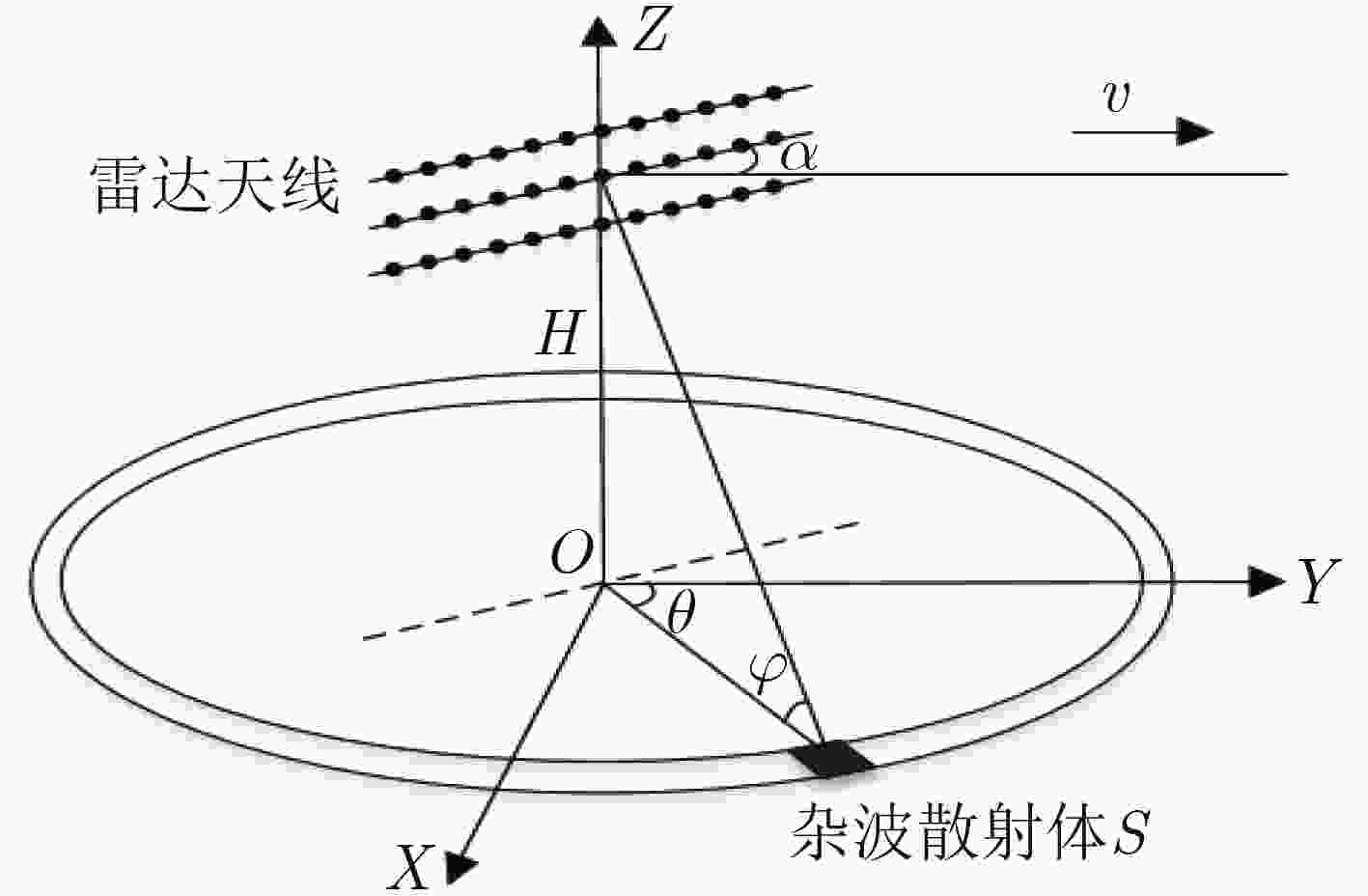
在非均匀杂波和密集目标环境下,由于没有足够的独立同分布(IID)训练样本,传统空时自适应处理(STAP)方法的杂波抑制性能严重下降。针对以上问题,该文提出一种对阵元误差稳健的机载面阵雷达非均匀杂波抑制方法。该方法首先根据雷达系统参数先验知识构造杂波表示基矩阵。然后在考虑阵元误差的情况下,基于最小二乘准则迭代地估计杂波表示系数和阵元误差,最后利用估计得到的最优杂波表示系数和阵元误差直接在阵元脉冲域进行杂波对消。该方法无须估计待检测单元统计特性;没有孔径损失;不需要训练样本;即使在距离模糊情况下也能有效地抑制密集目标环境下机载面阵雷达回波数据中的非均匀杂波。仿真结果验证了该文方法的有效性。
Abstract:Due to lack of enough Independent Identically Distributed (IID) training samples, it seriously degrades the clutter suppression performance of the traditional Space-Time Adaptive Processing (STAP) algorithms in heterogeneous clutter and target rich environment. To solve the problem, a heterogeneous clutter suppression method for the airborne plane array radar is proposed, which is robust to the array error. Firstly, the clutter representation basis matrix is constructed by the radar system parameters priori knowledge. Next, with the consideration of array error, it estimates iteratively the clutter representation coefficient and array error by the least square criterion. Finally, the clutter cancellation is conducted by the obtained optimal clutter representation coefficient and array error in element-pulse domain. The proposed method does not need to estimate the statistical properties of cell under test and has no aperture loss. In addition, it does not need any training sample and can suppress effectively the heterogeneous clutter of airborne planar array radar echo data in rich target environment even if range ambiguity exists. Simulation results verify the validity of the proposed method.
-
Key words:
- Airborne planar array radar /
- Rich target /
- Heterogeneous clutter /
- Clutter suppression
-
表 1 雷达系统参数
参数 值 俯仰阵元数 4 方位阵元数 8 阵元间距 0.05 m 脉冲数 24 脉冲重复频率 6000 Hz 工作波长 0.1 m 接收机带宽 2 MHz 飞机高度 4000 m 飞行速度 150 m/s 表 2 注入信号参数
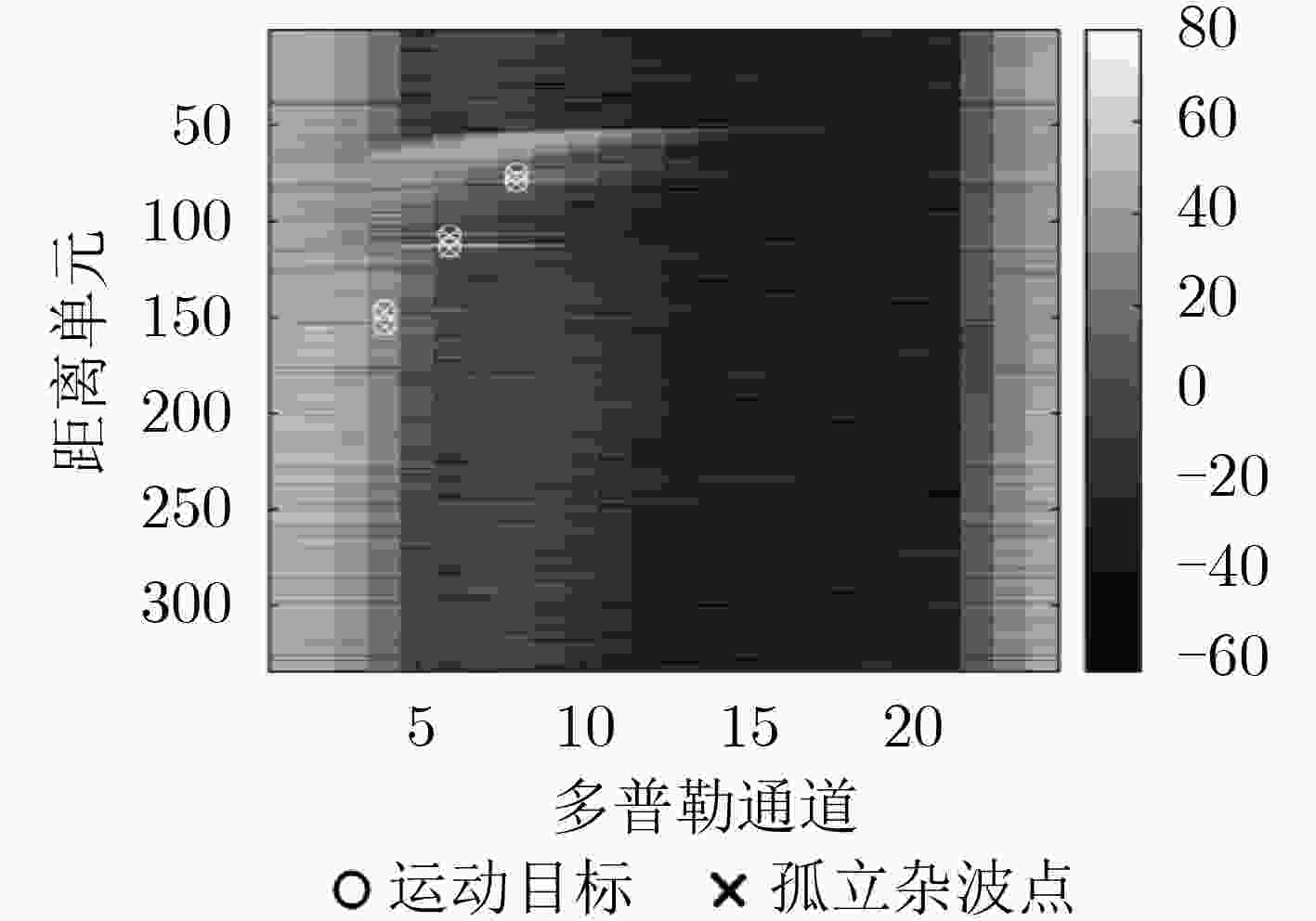
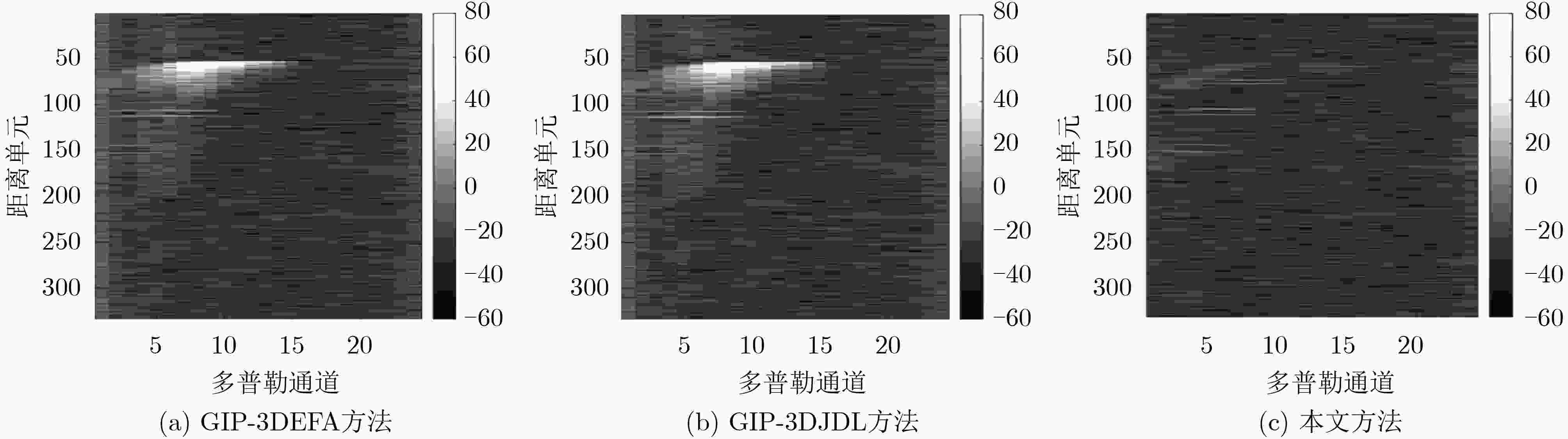
信号 距离单元 多普勒通道 信噪比(dB) ICP1/MT1 76/75 8 60/13 ICP2/MT2 80/79 8 60/13 ICP3/MT3 108/107 6 70/9 ICP4/MT4 114/113 6 70/9 ICP5/MT5 147/146 4 50/6 ICP6/MT6 155/154 4 50/6 表 3 雷达系统仿真参数
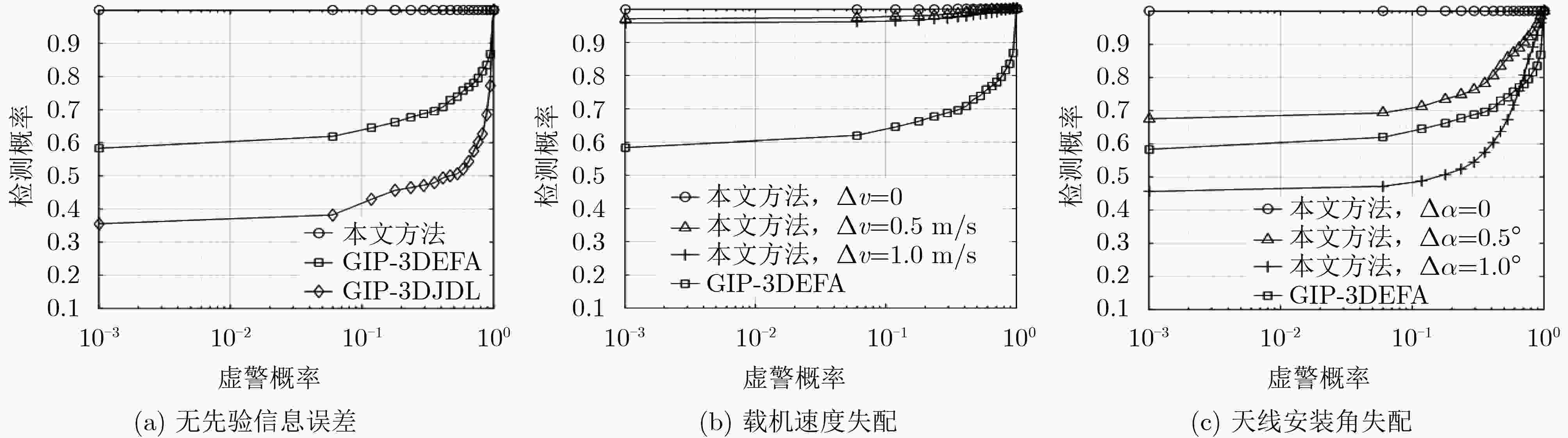
参数 值 俯仰向阵元数 2 方位向阵元数 11 脉冲数 128 飞行高度 3105.3 m 飞行速度 126.4 m/s 脉冲重复频率 1984 Hz 工作波长 0.2419 m -
WARD J. Space-time adaptive processing for airborne radar[R]. MIT Technical Report 1015, 1994. REED I S, MALLETT J D, and BRENNAN L E. Rapid convergence rate in adaptive arrays[J]. IEEE Transactions on Aerospace and Electronic Systems, 1974, AES-10(6): 853–863. doi: 10.1109/TAES.1974.307893 DIPIETRO R C. Extended factored space-time processing for airborne radar systems[C]. The 26th Asilomar Conference on Signals, Systems & Computers, Pacific Grove, USA, 1992: 425–430. KREYENKAMP O and KLEMM R. Doppler compensation in forward-looking STAP radar[J]. IEE Proceedings-Radar, Sonar and Navigation, 2001, 148(5): 253–258. doi: 10.1049/ip-rsn:20010557 SUN Ke, MENG Huadong, LAPIERRE F D, et al. Registration-based compensation using sparse representation in conformal-array STAP[J]. Signal Processing, 2011, 91(10): 2268–2276. doi: 10.1016/j.sigpro.2011.04.008 吕晓德, 杨璟茂, 岳琦, 等. 基于稀疏贝叶斯学习的机载双基雷达杂波抑制[J]. 电子与信息学报, 2018, 40(11): 2651–2658. doi: 10.11999/JEIT180062LÜ Xiaode, YANG Jingmao, YUE Qi, et al. Airborne bistatic radar clutter suppression based on sparse Bayesian learning[J]. Journal of Electronics &Information Technology, 2018, 40(11): 2651–2658. doi: 10.11999/JEIT180062 WANG Zetao, XIE Wenchong, DUAN Keqing, et al. Clutter suppression algorithm based on fast converging sparse Bayesian learning for airborne radar[J]. Signal Processing, 2017, 130: 159–168. doi: 10.1016/j.sigpro.2016.06.023 郑霖, 姚伟伟, 杨超, 等. 近距离慢速目标检测杂波抑制方法[J]. 电子与信息学报, 2018, 40(10): 2506–2512. doi: 10.11999/JEIT180031ZHENG Lin, YAO Weiwei, YANG Chao, et al. Clutter suppression method for short range slow moving target detection[J]. Journal of Electronics &Information Technology, 2018, 40(10): 2506–2512. doi: 10.11999/JEIT180031 YANG Zhaocheng, LI Xiang, WANG Hongqiang, et al. Adaptive clutter suppression based on iterative adaptive approach for airborne radar[J]. Signal Processing, 2013, 93(12): 3567–3577. doi: 10.1016/j.sigpro.2013.03.033 HAN Sudan, FAN Chongyi, and HUANG Xiaotao. A novel STAP based on spectrum-aided reduced-dimension clutter sparse recovery[J]. IEEE Geoscience and Remote Sensing Letters, 2017, 14(2): 213–217. doi: 10.1109/LGRS.2016.2635104 SUN Ke, MENG Huadong, WANG Yongliang, et al. Direct data domain STAP using sparse representation of clutter spectrum[J]. Signal Processing, 2011, 91(9): 2222–2236. doi: 10.1016/j.sigpro.2011.04.006 ABADIR K M and MAGNUS J R. Matrix Algebra[M]. Cambridge: Cambridge University Press, 2005. 中国科学院计算机网络信息中心. 国际科学数据服务平台[EB/OL]. http://globalchange.nsdc.cn.2014.7. 中国科学院计算机网络信息中心. 全球变化参量数据库[EB/OL]. http://globalchange.nsdc.cn.2014.7. MCARM data[EB/OL]. http://128.132.42.229.2018.8. -





 下载:
下载:



 下载:
下载:
