Soft Output Signal Detection for Massive MIMO Systems Based on Chebyshev Trace Iteration
-
摘要:
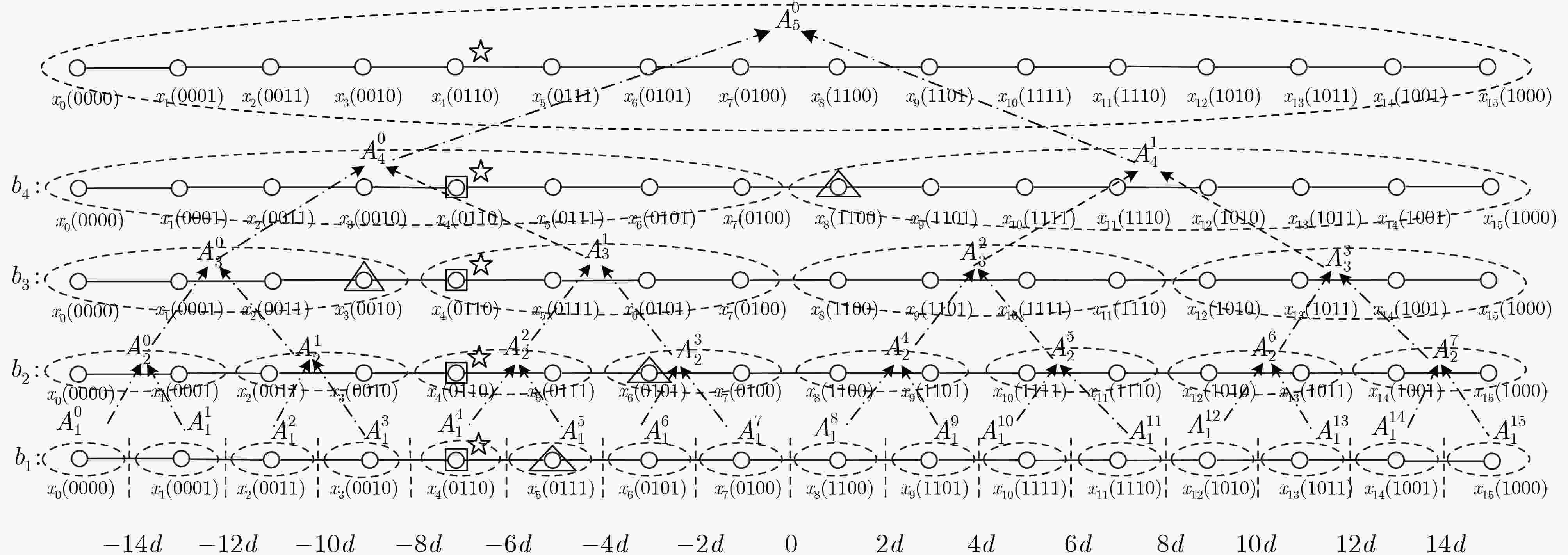
在多用户大规模多输入多输出(MIMO)系统信号检测算法中,最小均方误差(MMSE)算法可取得近似最优性能,但MMSE算法中高维矩阵求逆的复杂度过高,导致在实际应用中难以快速有效地实现。同时,对于高阶正交幅度调制(HQAM),如果符号向比特的解映射采用硬判决,将会导致后续信道译码的性能明显下降。因此,该文针对采用格雷编码的HQAM的多用户大规模MIMO系统,提出一种基于切比雪夫-迹迭代(CTI)的低复杂度软输出信号检测算法。该算法不但有效地规避了信号检测所需的高维矩阵求逆,同时,利用格雷编码的调制信号的比特翻转特性和二叉树结构,给出了一种融合三叉链表搜索的比特对数似然比(LLR)简化计算方法。仿真结果表明,该文所提的软输出信号检测算法最多需要3次迭代就能收敛并可取得接近MMSE算法的性能,在复杂度和性能之间取得了很好的折中。
-
关键词:
- 高阶正交幅度调制 /
- 切比雪夫-迹迭代 /
- 对数似然比 /
- 大规模多输入多输出系统
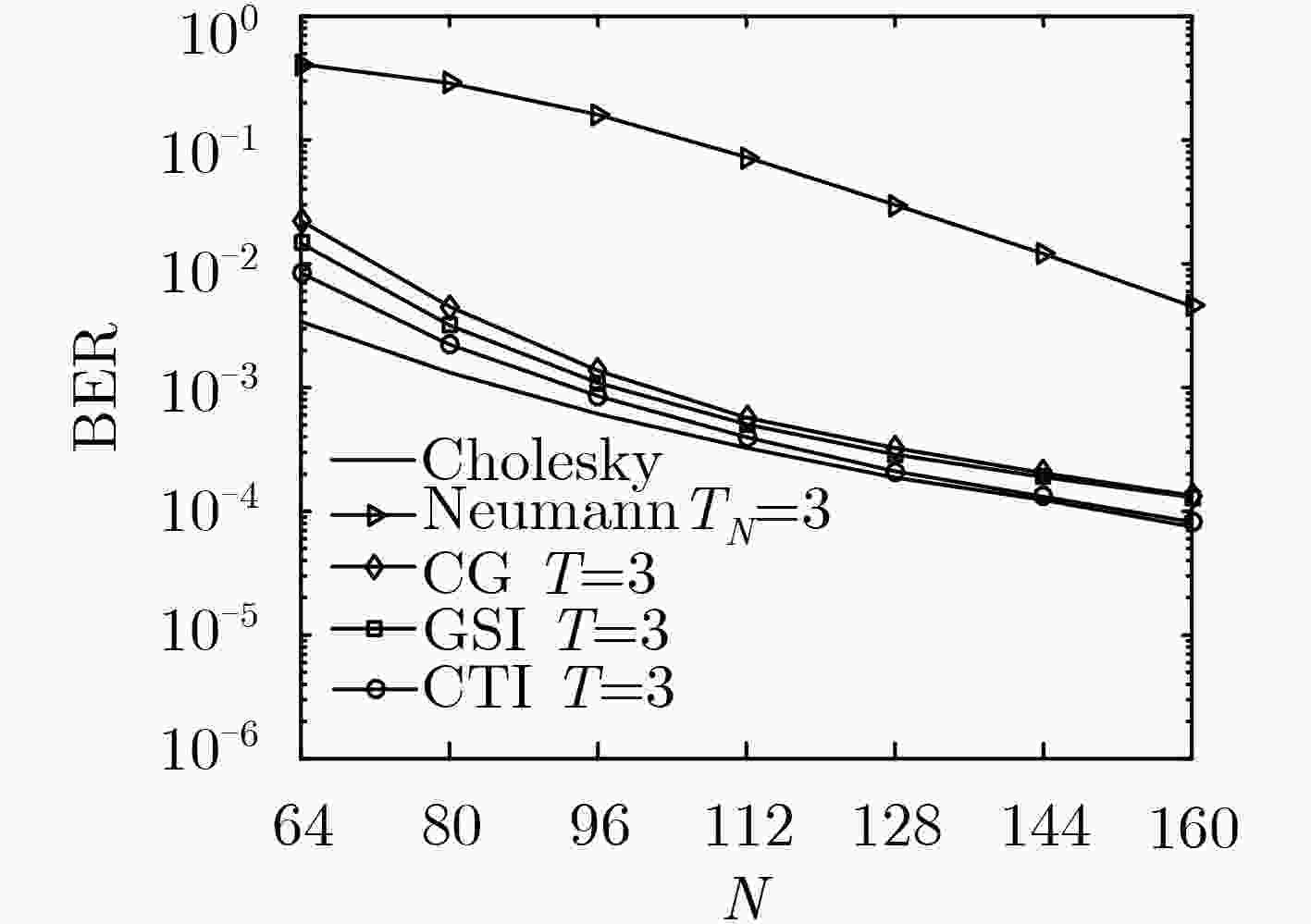
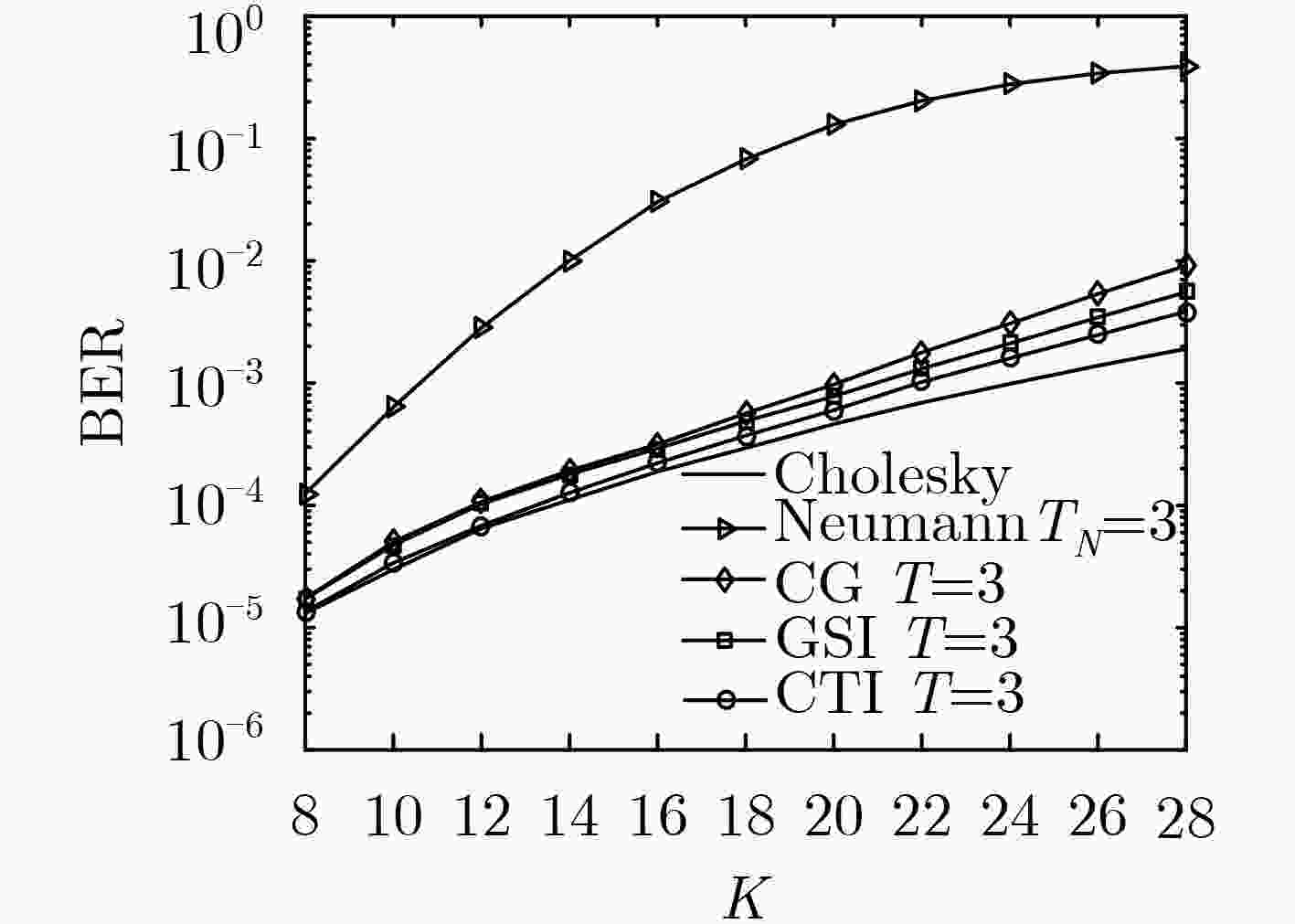
Abstract:Minimum Mean Square Error (MMSE) algorithm can achieve near-optimal detection performance for multi-user massive Multiple Input Multiple Output (MIMO) systems. However, the calculation of the high-dimensional matrix inversion required in MMSE algorithm causes excessively high computational complexity, which makes it difficult to implement quickly and effectively in practical applications. At the same time, for the Higher Quadrature Amplitude Modulation (HQAM), the direct use of hard decision to realize the symbol-to-bit demapper will result in an obvious performance loss. Therefore, a low-complexity soft output signal detection algorithm based on Chebyshev-Trace Iteration (CTI) is proposed for Gray-coded HQAM in this paper. The algorithm not only effectively avoids the calculation of the high dimensional matrix inversion, but also gives a simplified calculation method with the trident list searching to compute the bit Log-Likelihood Ratio (LLR) by using the bit flip property of Gray-coded modulation and binary tree architecture. The simulation results show that the proposed soft output detection algorithm needs at most 3 iterations to converge and achieve detection performance close to MMSE, which achieves a good tradeoff between the complexity and the detection performance.
-
表 1 基于CTI的软输出检测算法的步骤
输入:${{y}}{\rm{,}}{{H}},K,N,m,{\sigma ^2},T$ 初始化:${\overset{\frown}{{y} }} = {{{H}}^{\rm T}}{{y}};$${{W} } = { {{H} }^{\rm{T} } }{{H} } + \dfrac{ { {\sigma ^2} } }{2}{ {{I} }_{2K} }$; ${{D}}{\rm{ = Diag\{ }}{{W}}{\rm{\} }};$${{{x}}^{(0)}} = {{{D}}^{ - 1}}{\overset{\frown}{{y} }};$
${ {{x} }^{(1)} } = \left({ {{I} }_{2K} } - \dfrac{w}{ { {\rm{Tr} } ({{W} })} }{{W} }\right){ {{x} }^{(0)} } + \dfrac{w}{ { {\rm{Tr} } ({{W} })} }{\overset{\frown}{{y} } };{{ } }$ ${\rm{Tr} } ({{W} }) = \displaystyle\sum\limits_{n = 1}^{2K} { {W_{nn} } } ;$
${\eta _{\max }} = N{(1 + \sqrt {{K / N}} )^2}$; ${\eta _{\min }} = N{(1 - \sqrt {{K / N}} )^2}$; $w = {{2{\rm{Tr}} ({{W}})} / {({\eta _{\max }} + {\eta _{\min }})}}$; $f{\rm{ = 1/}}\left| {1 - {{w \cdot {\eta _{\min }}} / {{\rm{Tr}} ({{W}})}}} \right|$; ${C_0}(f) = 1;\;{C_1}(f) = f$(1) ${\rm{for} }$ $t = 1,2, ··· ,T - 1$ (2) ${C_{t + 1}}(f) = 2f{C_t}(f) - {C_{t - 1}}(f)$ (3) ${\lambda _{t + 1}} = {{2f{C_t}(f)} / {{C_{t + 1}}(f)}}$ (4) ${ {{x} }^{(t + 1)} } = {\lambda _{t + 1} }\left(\left({ {{I} }_{2K} } - \frac{w}{ { {\rm{Tr} } ({{W} })} }{{W} }\right){ {{x} }^{(t)} } + \frac{w}{ { {\rm{Tr} } ({{W} })} }{\overset{\frown}{{y} } } - { {{x} }^{(t - 1)} }\right) + { {{x} }^{(t - 1)} }$ (5) $t = t + 1$ (6) ${\rm{end \;for} }$ (7) ${\rm{for} }$ $i = 1,2, ··· ,2K$ (8) ${\rm{for} }$ $r = 1,2, ··· ,m$ (9)确定式(17) ${s^{\rm ML} }$及其下标${q^{{\rm{ML}} }}$和${s^{\rm ML} }$对应的格雷编码矢量${ {{b} }^ * } = (b_m^*\;b_{m - 1}^*\, ··· b_1^ * )$; (10)查询三叉链表获得$b_r^ * $对应的${B_r}$的值及其奇偶性 (11) ${\rm{if} }$ ${B_r}$是偶数 (12) $q_r^ * = {2^{r - 1}}({B_r} + 1)$ (13) ${\rm{else} }$ (14) $q_r^ * = {2^{r - 1}}{B_r} - 1$ (15) ${\rm{end \;if} }$
(16) $L_{i,r}^{(T)} = {( - 1)^{b_r^ * } } \cdot { { {W_{ii} } } }/{ { {\sigma ^2} } } \cdot \left( { { {\left| {x_i^{(T)} - {s_{q_r^ * } } } \right|}^2} - { {\left| {x_i^{(T)} - {s^{\rm ML} } } \right|}^2} } \right)$(17) $r = r + 1$ (18) ${\rm{end \;for} }$ (19) $i = i + 1$ (20) ${\rm{end \;for} }$ (21) $L_{i,r}^{(T)}$ -
ALBREEM M A, JUNTTI M, and SHAHABUDDIN S. Massive MIMO detection techniques: A survey[J]. IEEE Communications Surveys & Tutorials, 2019, 21(4): 3109–3132. doi: 10.1109/COMST.2019.2935810 LI Peng and MURCH R D. Multiple output selection-LAS algorithm in large MIMO systems[J]. IEEE Communications Letters, 2010, 14(5): 399–401. doi: 10.1109/LCOMM.2010.05.100092 DATTA T, SRINIDHI N, CHOCKALINGAM A, et al. Random-restart reactive tabu search algorithm for detection in large-MIMO systems[J]. IEEE Communications Letters, 2010, 14(12): 1107–1109. doi: 10.1109/LCOMM.2010.101210.101587 TAN Xiaosi, UENG Y L, ZHANG Zaichen, et al. A low-complexity massive MIMO detection based on approximate expectation propagation[J]. IEEE Transactions on Vehicular Technology, 2019, 68(8): 7260–7272. doi: 10.1109/TVT.2019.2924952 金思年, 岳殿武, 闫秋娜. 基于迫零方式下带有硬件损害的大规模MIMO全双工中继系统[J]. 电子与信息学报, 2019, 41(6): 1352–1358. doi: 10.11999/JEIT180228JIN Sinian, YUE Dianwu, and YAN Qiuna. Massive MIMO full-duplex relaying with hardware impairments and zero-forcing processing[J]. Journal of Electronics &Information Technology, 2019, 41(6): 1352–1358. doi: 10.11999/JEIT180228 WU M, YIN Bei, WANG Guohui, et al. Large-scale MIMO detection for 3GPP LTE: Algorithms and FPGA implementations[J]. IEEE Journal of Selected Topics in Signal Processing, 2014, 8(5): 916–929. doi: 10.1109/JSTSP.2014.2313021 JIN Fangli, LIU Qiufeng, LIU Hao, et al. A low complexity signal detection scheme based on improved newton iteration for massive MIMO systems[J]. IEEE Communications Letters, 2019, 23(4): 748–751. doi: 10.1109/LCOMM.2019.2897798 HU Yuting, WANG Zhongxu, GAO Xinyu, et al. Low-complexity signal detection using CG method for uplink large-scale MIMO systems[C]. 2014 IEEE International Conference on Communication Systems, Macau, China, 2014: 477–481. doi: 10.1109/ICCS.2014.7024849. PENG Guiqiang, LIU Leibo, ZHANG Peng, et al. Low-computing-load, high-parallelism detection method based on Chebyshev iteration for massive MIMO systems with VLSI architecture[J]. IEEE Transactions on Signal Processing, 2017, 65(14): 3775–3788. doi: 10.1109/TSP.2017.2698410 DAI Linglong, GAO Xinyu, SU Xin, et al. Low-complexity soft-output signal detection based on gauss–Seidel method for uplink multiuser large-scale MIMO systems[J]. IEEE Transactions on Vehicular Technology, 2015, 64(10): 4839–4845. doi: 10.1109/TVT.2014.2370106 SHARIFFAR F, REFAHI SHEIKHANI A H, and NAJAFI H S. An efficient chebyshev semi-iterative method for the solution of large systems[J]. University Politehnica of Bucharest Scientific Bulletin-Series A, 2018, 80(4): 239–252. 路新华, CARLES NAVARRO M, 王忠勇, 等. 大规模MIMO系统上行链路时间-空间结构信道估计算法[J]. 电子与信息学报, 2020, 42(2): 519–525. doi: 10.11999/JEIT180676LU Xinhua, CARLES NAVARRO M, WANG Zhongyong, et al. Channel estimation algorithm using temporal-spatial structure for up-link of massive MIMO systems[J]. Journal of Electronics &Information Technology, 2020, 42(2): 519–525. doi: 10.11999/JEIT180676 GAO Xinyu, DAI Linglong, YUEN C, et al. Low-complexity MMSE signal detection based on Richardson method for large-scale MIMO systems[C]. The 2014 IEEE 80th Vehicular Technology Conference, Vancouver, Canada, 2014: 1–5. doi: 10.1109/VTCFall.2014.6966041. ZHOU Jiangyun, HU Jianhao, CHEN Jienan, et al. Biased MMSE soft-output detection based on conjugate gradient in massive MIMO[C]. The 2015 IEEE 11th International Conference on ASIC, Chengdu, China, 2015: 1–4. doi: 10.1109/ASICON.2015.7517204. BHAT G S and SAVAGE C D. Balanced gray codes[J]. The Electronic Journal of Combinatorics, 1996, 3(1): R25. -





 下载:
下载:



 下载:
下载:
