The Optimization of Wireless Sensor Network Topology Based on FW-PSO Algorithm
-
摘要:
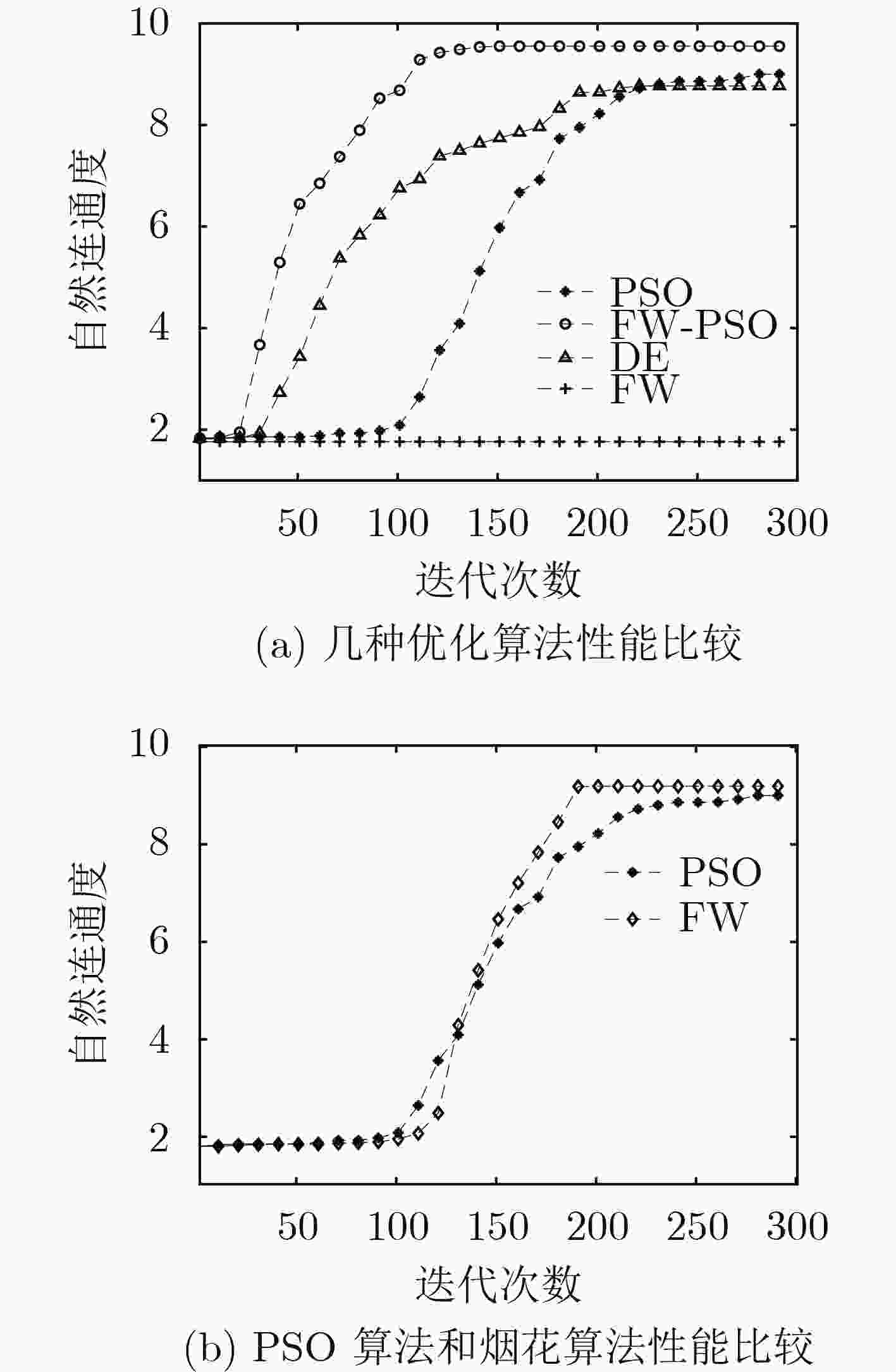
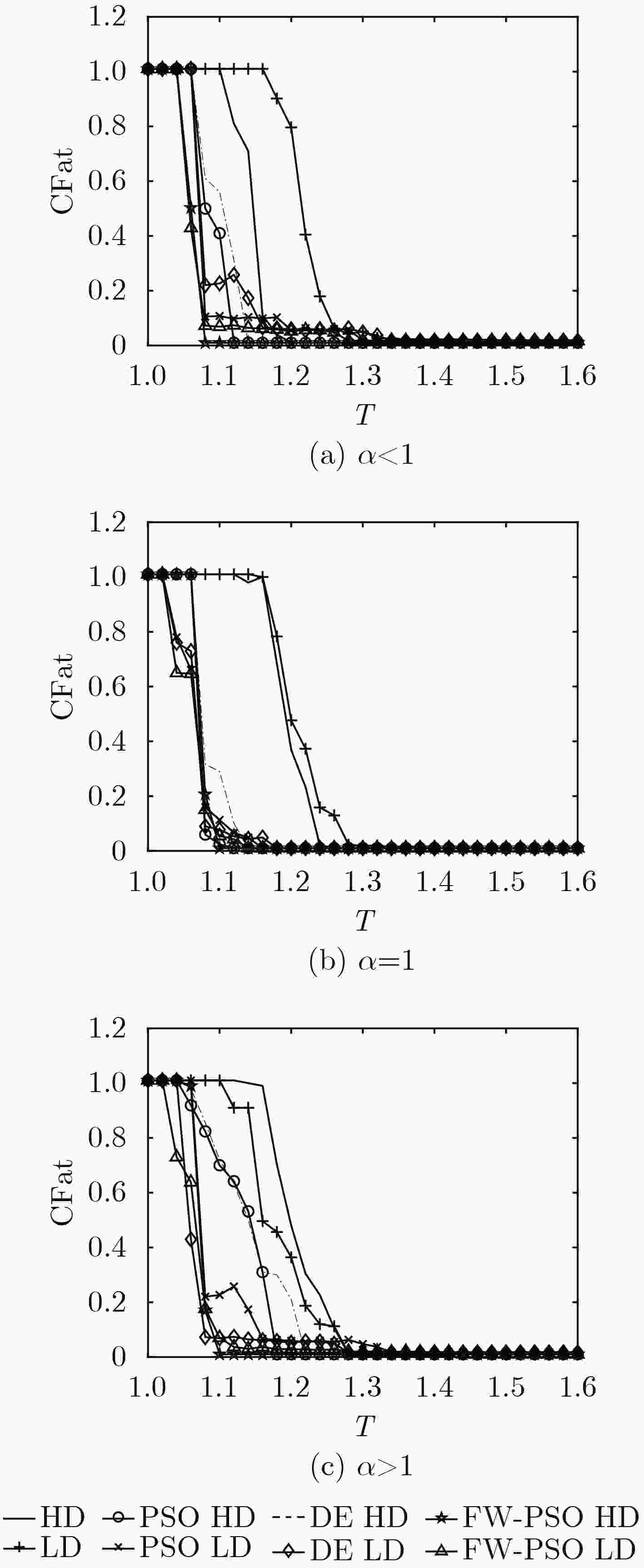
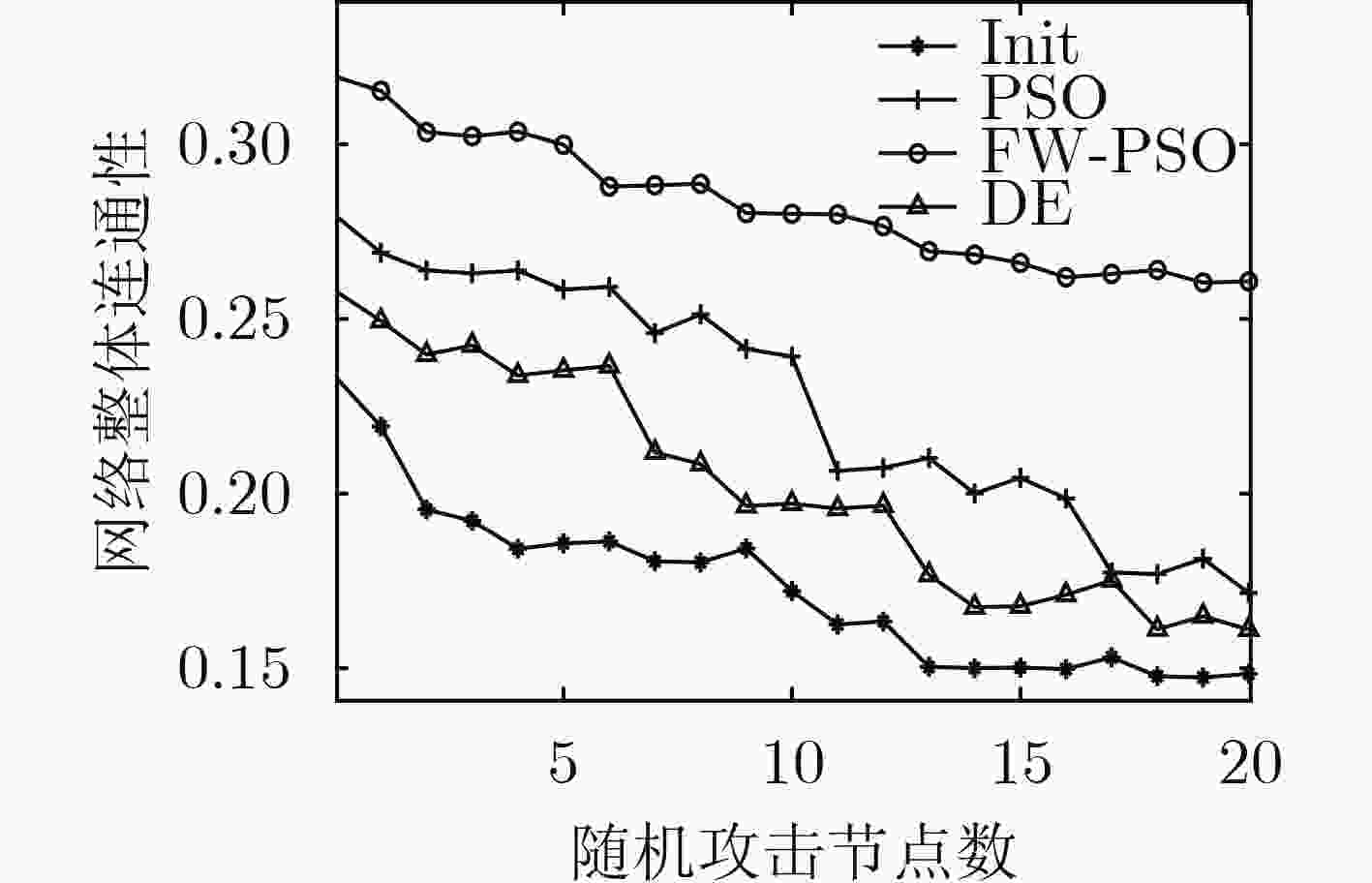
无线传感网络(WSN)具有无标度网络的特征,通常工作在无人值守的开放性环境中,极易遭受到各种蓄意攻击。攻击使得网络发生故障,甚至会导致整个网络瘫痪。该文基于复杂网络领域的无标度网络,构建具有无标度特性的无线传感网络模型。利用烟花算法及粒子群算法(PSO)寻优过程中的搜索能力、种群多样性等优点,提出了一种FW-PSO算法,该算法在全局搜索能力和收敛速度上具有较好的性能。针对具有无标度特性的网络模型,用FW-PSO算法对网络拓扑进行优化,在不同的攻击策略下分别从动态抗毁性和静态抗毁性分析优化前后网络的性能。仿真实验表明,与其他同类算法相比,经过该文所提算法优化后的无线传感网络的动态和静态抗毁性能都有明显提升。
Abstract:Wireless Sensor Network (WSN) has the characteristics of scale-free network, usually works in an unattended open environment, and is vulnerable to a variety of deliberate attacks. The attack causes the network to break down, and even causes the whole network to be paralyzed. In this paper, the scale-free network in complex network is taken as the research object, and a scale-free wireless sensor network model is constructed. Using the advantages of Fireworks algorithm and Particle Swarm Optimization (PSO) algorithm, such as search ability and population diversity, the FW-PSO (FireWorks and Particle Swarm Optimization) algorithm is proposed, which has good performance in global search ability and convergence speed. For the scale-free network model, FW-PSO algorithm is used to optimize the network topology. Under different attack strategies, the performance of the network before and after the optimization is analyzed from dynamic and static invulnerability respectively. Simulation results show that, compared with other similar algorithms, the dynamic and static invulnerability of wireless sensor network optimized by the proposed algorithm has obvious advantages.
-
表 1 FW-PSO算法的伪代码
FW-PSO算法: 1. -- fpbest: 个体的最佳适应度值 2. -- fgbest: 群体的最佳适应度值 3. 输入:目标函数$f\left( x \right)$,邻接矩阵${{A}}\left( G \right)$; 4. 参数初始化: gronum, $n,{c_1},{c_2},{w_{\max } },{w_{\min } },{ { {{\rm{gen}}} }_{\max } }, A,M, a,b$,
maxgen5. Set ${\rm{fpbes}}{{\rm{t}}_i} \leftarrow {x_i}\left( { {x_i} \in 1,2, \cdots ,{\rm{gronum}}} \right)$, ${ { {{\rm{gen}}} }_{\max } } \leftarrow 1$ 6. While ${\rm{gen}} < { { {{\rm{gen}}} }_{\max } }$ 7. for ${\rm{pgen}} \leftarrow 1$ to maxgen 8. for $i \leftarrow 1$ to gronum 9. 更新粒子的${v_i},{x_i}$ by式(6)、式(7) 10. 计算$f\left( {{x_i}} \right)$ 11. if $f\left( { {x_i} } \right) > {\rm{fpbest}}\left( { {x_i} } \right)$ 12. then ${\rm{fpbest}}\left( { {x_i} } \right) \leftarrow f\left( { {x_i} } \right)$ 13. end if 14. if $f\left( { {x_i} } \right) < {\rm{fpbest}}\left( { {x_i} } \right)$ 15. then $f\left( { {x_i} } \right) \leftarrow {\rm{fpbest}}\left( { {x_i} } \right)$ 16. end if 17. end for 18. ${\rm{pgen}} \leftarrow {\rm{pgen}} + 1$ 19. end for 20. 将粒子组按降序排序,选出适合度较好的n个粒子,并根
据3.2节FW-PSO算法选出n个最优粒子21. 计算新种群的fpbest,fgbest 22. ${\rm{gen}} \leftarrow {\rm{gen}} + 1$ 23. end while 24. 输出:fgbest 表 2 仿真参数设置
参数仿真 参数值 网络节点数gronum 100 网络边数W 191 加速因子${c_1},{c_2}$ 1.49445 最小惯性权重${w_{\min }}$ 0.4 最大惯性权重${w_{\max }}$ 0.9 PSO算法保留的最优粒子数n 40 爆炸数目调节因子A 5 爆炸数目调节因子M 6 爆炸数目限制因子a 0.3 爆炸数目限制因子b 0.6 机器精度$\varepsilon $ $2.2204 \times {10^{ - 16}}$ 变异火花数 10 总迭代次数${ { {{\rm{gen}}} }_{\max } }$ 100 PSO迭代次数maxgen 300 -
郝晓辰, 刘金硕, 姚宁, 等. 无线传感器网络基于容量和传输能耗的功率与信道联合博弈算法[J]. 电子与信息学报, 2018, 40(7): 1715–1722. doi: 10.11999/JEIT170927HAO Xiaochen, LIU Jinshuo, YAO Ning, et al. Research of network capacity and transmission energy consumption in WSNs based on game theory[J]. Journal of Electronics &Information Technology, 2018, 40(7): 1715–1722. doi: 10.11999/JEIT170927 秦宁宁, 金磊, 许健, 等. 邻近信息约束下的随机异构无线传感器网络节点调度算法[J]. 电子与信息学报, 2019, 41(10): 2310–2317. doi: 10.11999/JEIT190094QIN Ningning, JIN Lei, XU Jian, et al. Neighbor information constrained node scheduling in stochastic heterogeneous wireless sensor networks[J]. Journal of Electronics &Information Technology, 2019, 41(10): 2310–2317. doi: 10.11999/JEIT190094 吕敬祥, 罗文浪. 无线传感网络量化及能量优化策略[J]. 电子与信息学报, 2020, 42(5): 1118–1124. doi: 10.11999/JEIT190185LÜ Jingxiang and LUO Wenlang. Quantization and energy optimization strategy of wireless sensor networks[J]. Journal of Electronics &Information Technology, 2020, 42(5): 1118–1124. doi: 10.11999/JEIT190185 YAMASHITA K, NAKAMURA R, and OHSAKI H. A study on robustness of complex networks against random node removals[C]. The 42nd IEEE Annual Computer Software and Applications Conference (COMPSAC), Tokyo, Japan, 2018: 966–969. QIU Tie, LIU Jie, SI Weisheng, et al. Robustness optimization scheme with multi-population Co-Evolution for Scale-Free Wireless Sensor Networks[J]. IEEE/ACM Transactions on Networking, 2019, 27(3): 1028–1042. doi: 10.1109/TNET.2019.2907243 MOTTER A E and LAI Yingcheng. Cascade-based attacks on complex networks[J]. Physical Review E, 2003, 66(2): 065102(R). doi: 10.1103/PhysRevE.66.065102 D’SOUZA R M, BRUMMITT C D, and LEICHT E A. Modeling Interdependent Networks as Random Graphs: Connectivity and Systemic Risk[M]. D’AGOSTINO G and SCALA A. Networks of Networks: The Last Frontier of Complexity. Cham: Springer, 2014: 73–94. 崔文岩, 孟相如, 康巧燕, 等. 基于复合边权重的加权复杂网络级联抗毁性优化[J]. 系统工程与电子技术, 2017, 39(2): 355–361. doi: 10.3969/j.issn.1001-506X.2017.02.19CUI Wenyan, MENG Xiangru, KANG Qiaoyan, et al. Optimization of cascading invulnerability on weighted complex networks based on composite edge weight model[J]. Systems Engineering and Electronics, 2017, 39(2): 355–361. doi: 10.3969/j.issn.1001-506X.2017.02.19 WANG Wenxu and CHEN Guanrong. Universal robustness characteristic of weighted networks against cascading failure[J]. Physical Review E, 2008, 77(2): 026101. doi: 10.1103/PhysRevE.77.026101 HOU Yueyi, XING Xiaoyun, LI Menghui, et al. Overload cascading failure on complex networks with heterogeneous load redistribution[J]. Physica A: Statistical Mechanics and its Applications, 2017, 481: 160–166. doi: 10.1016/j.physa.2017.04.039 REN Wendi, WU Jiajing, ZHANG Xi, et al. A stochastic model of cascading failure dynamics in communication networks[J]. IEEE Transactions on Circuits and Systems II: Express Briefs, 2018, 65(5): 632–636. doi: 10.1109/TCSII.2018.2822049 尹荣荣, 刘彬, 刘浩然, 等. 无线传感器网络中无标度拓扑的动态容错性分析[J]. 物理学报, 2014, 63(11): 110205. doi: 10.7498/aps.63.110205YIN Rongrong, LIU Bin, LIU Haoran, et al. Dynamic fault-tolerance analysis of scale-free topology in wireless sensor networks[J]. Acta Physica Sinica, 2014, 63(11): 110205. doi: 10.7498/aps.63.110205 李黎, 郑庆华, 管晓宏. 基于有限资源提升网络可生存性的拓扑重构方法[J]. 物理学报, 2014, 63(17): 170201. doi: 10.7498/aps.63.170201LI Li, ZHENG Qinghua, and GUAN Xiaohong. A topological reconfiguration method for enhancing networks survivability with limited resources[J]. Acta Physica Sinica, 2014, 63(17): 170201. doi: 10.7498/aps.63.170201 WANG Jianwei and RONG Lili. Cascade-based attack vulnerability on the US power grid[J]. Safety Science, 2009, 47(10): 1332–1336. doi: 10.1016/j.ssci.2009.02.002 WANG Jianwei, RONG Lili, ZHANG Liang, et al. Attack vulnerability of scale-free networks due to cascading failures[J]. Physica A: Statistical Mechanics and its Applications, 2008, 387(26): 6671–6678. doi: 10.1016/j.physa.2008.08.037 庄雷, 田帅魁, 和孟佯, 等. 基于滑动区域的粒子群虚拟网节能映射算法[J]. 电子与信息学报, 2019, 41(12): 3029–3035. doi: 10.11999/JEIT190168ZHUANG Lei, TIAN Shuaikui, HE Mengyang, et al. Energy-saving virtual network embedding algorithm based on sliding region particle swarm[J]. Journal of Electronics &Information Technology, 2019, 41(12): 3029–3035. doi: 10.11999/JEIT190168 ZHANG Bei, ZHENG Yujun, ZHANG Minxia, et al. Fireworks algorithm with enhanced fireworks interaction[J]. IEEE/ACM Transactions on Computational Biology and Bioinformatics, 2017, 14(1): 42–55. doi: 10.1109/TCBB.2015.2446487 ZHANG Xiaoling and GODSIL C. Connectivity and minimal distance spectral radius of graphs[J]. Linear and Multilinear Algebra, 2011, 59(7): 745–754. doi: 10.1080/03081087.2010.499512 -





 下载:
下载:



 下载:
下载:
