一种量子图像的中值滤波方案

赵娅; 郭嘉慧; 李盼池

doi:10.11999/JEIT191038

一种量子图像的中值滤波方案

doi: 10.11999/JEIT191038

东北石油大学计算机与信息技术学院大庆 163318

基金项目: 国家自然科学基金(61702093)，东北石油大学青年科学基金(2020QNL-08)

详细信息

作者简介:
赵娅：女，1980年生，副教授，研究方向为量子衍生计算和量子图像处理

郭嘉慧：女，1995年生，硕士生，研究方向为量子图像处理

李盼池：男，1969年生，教授，研究方向为量子衍生计算和量子图像处理

通讯作者:
李盼池　lipanchi@vip.sina.com

中图分类号: TP391
计量
- 文章访问数: 1784
- HTML全文浏览量: 718
- PDF下载量: 95
- 被引次数: 0
出版历程
- 收稿日期: 2019-12-25
- 修回日期: 2020-07-08
- 网络出版日期: 2020-07-22
- 刊出日期: 2021-01-15

A Median Filtering Scheme for Quantum Images

School of Computer and Information Technology, Northeast Petroleum University, Daqing 163318, China

Funds: The National Natural Science Foundation of China (61702093), The Youth Science Foundation of Northeast Petroleum University (2020QNL-08)

摘要

摘要:
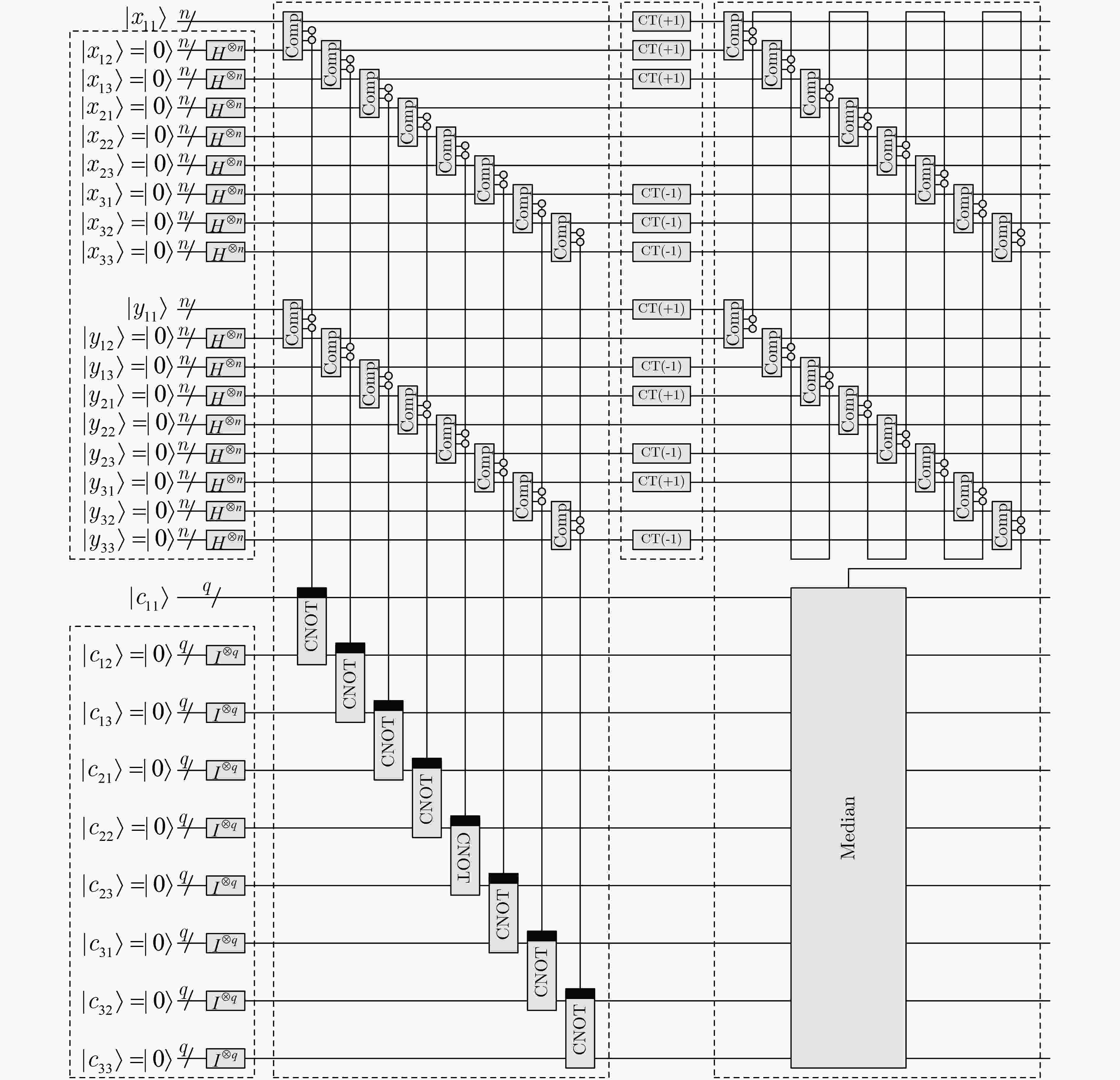
中值滤波是经典图像处理中的基本滤波方法，然而在量子图像处理中相关模型尚不多见。为解决量子图像的中值滤波问题，该文提出了基于量子中值计算的新方法。该方法采用迭代比较的方法将目标像素排序，进而得到中值。文中首先介绍了实现中值滤波所需的各种基本模块的量子线路，然后重点介绍了中值计算的量子实现方法，最后给出了量子图像中值滤波的总体线路框架。复杂度分析表明该方法具有对经典算法的指数加速。经典计算机上的仿真结果验证了提出方法的有效性及可行性。
- 图像处理 /
- 量子计算 /
- 量子图像处理 /
- 量子图像中值滤波
Abstract:
Median filtering is the basic filtering method in classical image processing. However, the corresponding models are still rare in quantum image processing. To address the median filtering of quantum images, a new method based on quantum median calculation is proposed. The method uses an iterative comparison method to sort the target pixels to obtain a median value. Firstly, the quantum circuits of various basic modules needed to implement median filtering are introduced. Then the quantum implementation method of median calculation is presented in detail. Finally, the overall circuit frame of quantum image median filtering is given. The complexity analysis shows that the method has exponential acceleration for its classical counterpart. The simulation results on the classical computer verify the validity and feasibility of the proposed method.
- Image processing /
- Quantum computing /
- Quantum image processing /
- Quantum image median filtering

HTML全文

图 1 一幅2×2的灰度图像

下载: 全尺寸图片幻灯片

图 2 量子比较器线路

下载: 全尺寸图片幻灯片

图 3 量子模加法器线路

下载: 全尺寸图片幻灯片

图 4 复制模块的量子线路

下载: 全尺寸图片幻灯片

图 5 复制模块的量子线路

下载: 全尺寸图片幻灯片

图 6 C2, C3, C9模块的量子线路

下载: 全尺寸图片幻灯片

图 7 中值计算模块的量子线路

下载: 全尺寸图片幻灯片

图 8 中值计算模块的量子线路

下载: 全尺寸图片幻灯片

图 9 仿真中用到的5幅灰度图像

下载: 全尺寸图片幻灯片

图 10 不同概率阈值下的量子比特翻转噪声图像

下载: 全尺寸图片幻灯片

图 11 不同概率阈值下量子噪声图像的滤波效果

下载: 全尺寸图片幻灯片

表 1 循环比较算法

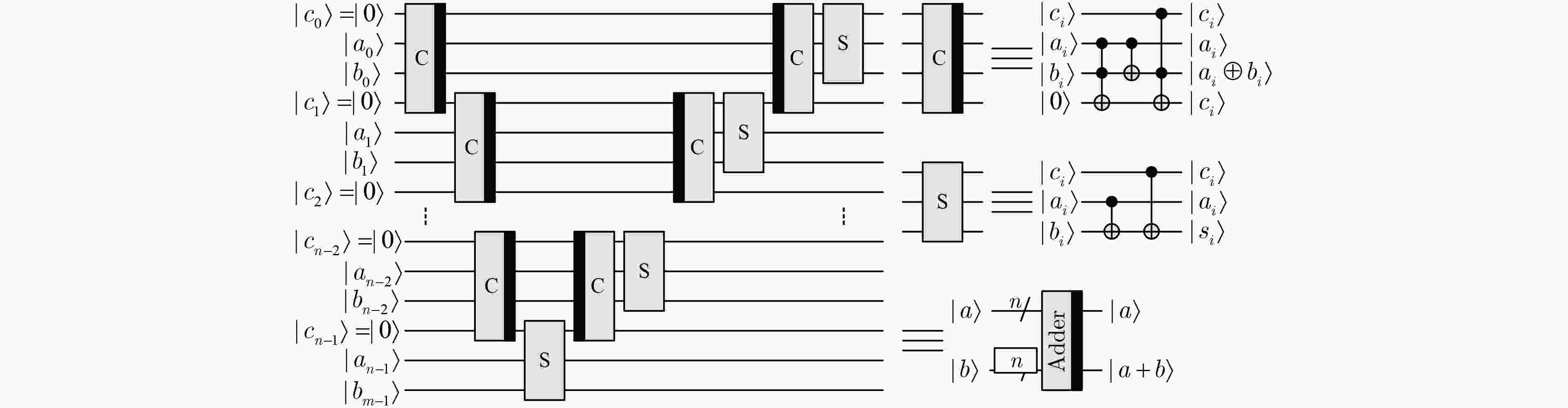
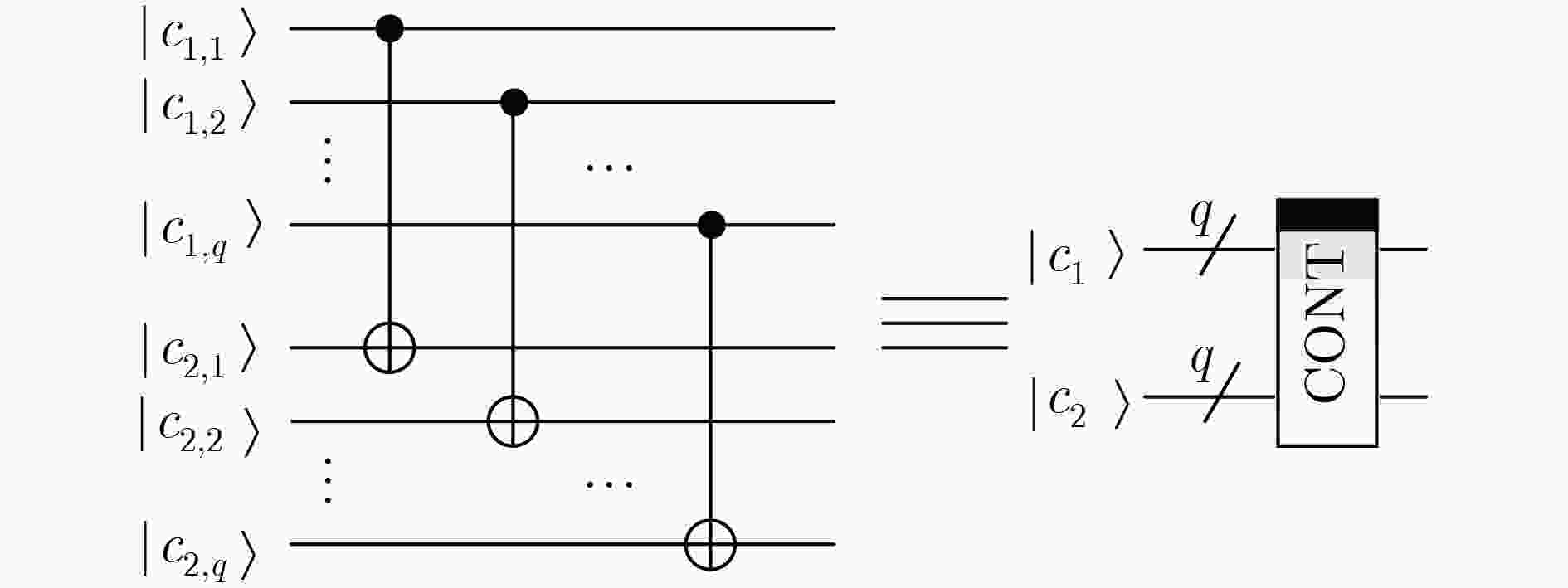
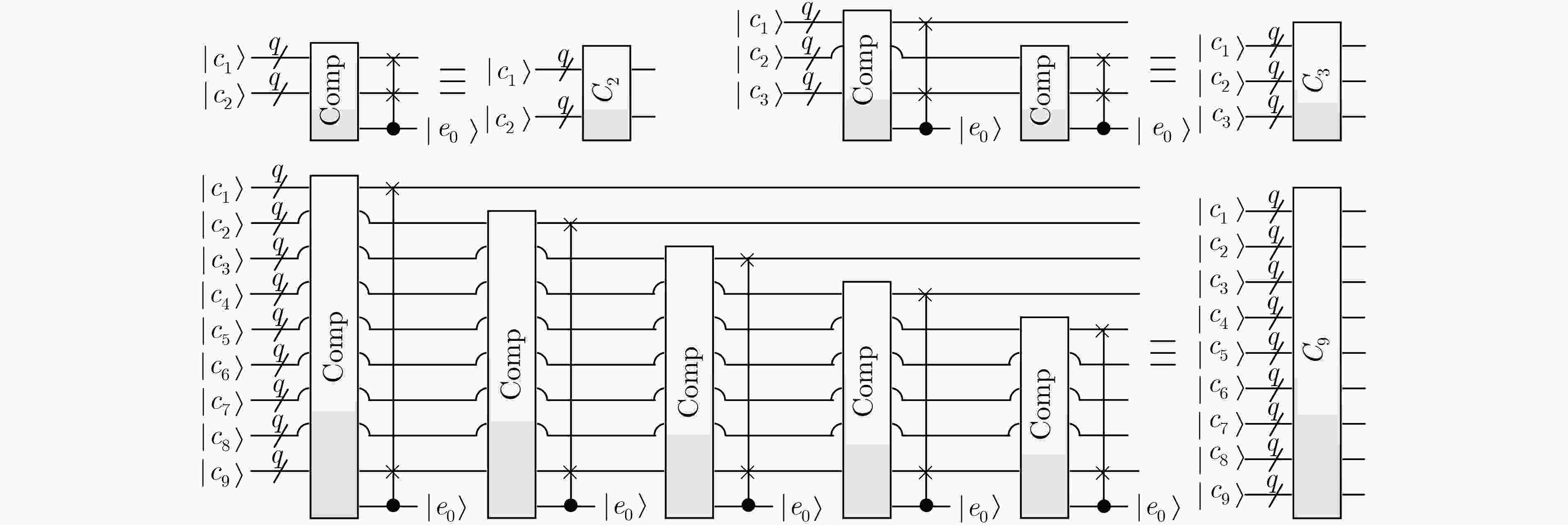
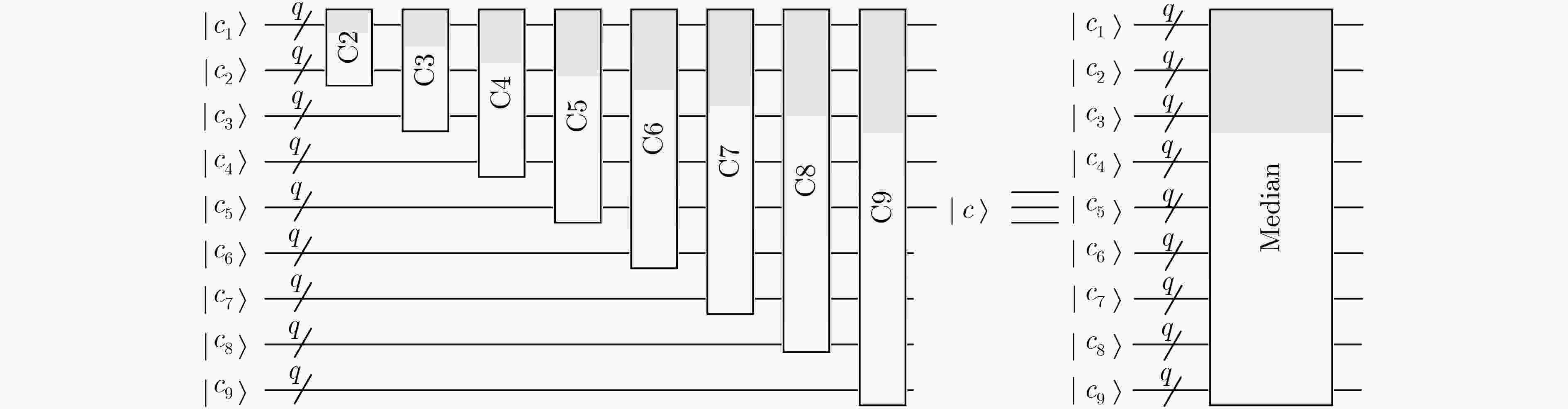
循环比较算法的具体实现
循环($i = 2\;\;{\rm{to}}\;\;9$)
如果$i < 9$，则$k = i - 1$，否则$k = i - 4$
循环($j = 1\;\;{\rm{to}}\;\;k$)
比较${c_j},{c_i}$，若${c_j} < {c_i}$，则交换${c_j},{c_i}$

下载: 导出CSV

表 2 两种方案滤波前后的峰值信噪比对比(dB)

图像	椒盐噪声					高斯噪声					泊松噪声
图像	滤波前	经典方案		本文方案		滤波前	经典方案		本文方案		滤波前	经典方案		本文方案
(a)	14.45	32.28	17.83	34.35	19.90	18.48	28.95	10.47	29.27	10.79	27.66	35.50	7.84	35.63	7.97
(b)	14.73	32.72	17.99	34.87	20.14	18.08	28.91	10.83	29.19	11.11	27.23	35.74	8.51	35.84	8.61
(c)	14.75	30.86	16.11	32.30	17.55	17.91	28.51	10.60	28.78	10.87	25.87	33.42	7.55	33.52	7.65
(d)	14.83	30.69	15.86	31.93	17.10	17.80	28.07	10.27	28.34	10.54	25.62	32.70	7.08	32.80	7.18
(e)	14.68	31.55	16.87	33.20	18.52	17.97	28.66	10.69	28.95	10.98	26.68	34.55	7.87	34.67	7.99
平均	14.69	31.62	16.93	33.33	18.64	18.05	28.62	10.57	28.91	10.86	26.61	34.38	7.77	34.49	7.88

下载: 导出CSV

表 3 量子噪声图像滤波前后的峰值信噪比对比(dB)

图像	概率阈值0.05			概率阈值0.06			概率阈值0.08			概率阈值0.10
图像	滤波前	滤波后		滤波前	滤波后		滤波前	滤波后		滤波前	滤波后
(a)	18.89	36.07	17.18	18.14	35.36	17.22	17.07	33.90	16.83	16.19	32.27	16.08
(b)	18.88	36.36	17.48	18.15	35.88	17.73	17.03	34.42	17.39	16.16	33.00	16.84
(c)	18.63	33.29	14.66	17.96	33.03	15.07	16.91	32.36	15.45	16.07	31.42	15.35
(d)	18.64	33.70	15.06	17.98	32.41	14.43	16.91	31.78	14.87	16.07	30.80	14.73
(e)	18.79	35.52	16.73	18.10	34.24	16.14	16.93	33.19	16.26	16.09	31.99	15.9
平均	18.77	34.99	16.22	18.07	34.18	16.12	16.97	33.13	16.16	16.12	31.90	15.78

下载: 导出CSV

参考文献(30)

FEYNMAN R P. Simulating physics with computers[J]. International Journal of Theoretical Physics, 1982, 21(6/7): 467–488.

SHOR P W. Algorithms for quantum computation: Discrete logarithms and factoring[C]. The 35th Annual Symposium on Foundations of Computer Science, Santa Fe, USA, 1994: 124–134.

GROVER L K. A fast quantum mechanical algorithm for database search[C]. The 28th Annual ACM Symposium on the Theory of Computing, Philadelphia, USA, 1996: 212–219.

VLASOV A Y. Quantum computations and images recognition[J]. arXiv: Quant-ph/9703010, 1997.

BEACH G, LOMONT C, and COHEN C. Quantum image processing (QuIP)[C]. The 32nd Applied Imagery Pattern Recognition Workshop, Washington, USA, 2003: 39–44.

YAN Fei, ILIYASU A M, and LE P Q. Quantum image processing: A review of advances in its security technologies[J]. International Journal of Quantum Information, 2017, 15(3): 1730001. doi: 10.1142/S0219749917300017

姜楠. 量子图像处理[M]. 北京: 清华大学出版社, 2016: 3–4.

JIANG Nan. Quantum Image Processing[M]. Beijing: Tsinghua Press, 2016: 3–4.

VENEGAS-ANDRACA S E and BOSE S. Storing, processing, and retrieving an image using quantum mechanics[J]. SPIE, 2003, 5105: 137–147.

LATORRE J I. Image compression and entanglement[J]. arXiv: Quant-ph/0510031, 2005.

VENEGAS-ANDRACA S E and BALL J L. Processing images in entangled quantum systems[J]. Quantum Information Processing, 2010, 9(1): 1–11. doi: 10.1007/s11128-009-0123-z

LEE P Q, DONG Fangyan, and HIROTA K. A flexible representation of quantum images for polynomial preparation, image compression, and processing operations[J]. Quantum Information Processing, 2011, 10(1): 63–84. doi: 10.1007/s11128-010-0177-y

ZHANG Yi, LU Kai, and GAO Yinghui, et al. NEQR: A novel enhanced quantum representation of digital images[J]. Quantum Information Processing, 2013, 12(8): 2833–2860. doi: 10.1007/s11128-013-0567-z

ZHOU Rigui, TAN Canyun, and IAN Hou. Global and local translation designs of quantum image based on FRQI[J]. International Journal of Theoretical Physics, 2017, 56(4): 1382–1398. doi: 10.1007/s10773-017-3279-9

JIANG Nan, WU Wenya, WANG Luo, et al. Quantum image pseudocolor coding based on the density-stratified method[J]. Quantum Information Processing, 2015, 14(5): 1735–1755. doi: 10.1007/s11128-015-0986-0

ZHOU Rigui, SUN Yajuan, and FAN Ping. Quantum image Gray-code and bit-plane scrambling[J]. Quantum Information Processing, 2015, 14(5): 1717–1734. doi: 10.1007/s11128-015-0964-6

ZHANG Yi, LU Kai, XU Kai, et al. Local feature point extraction for quantum images[J]. Quantum Information Processing, 2015, 14(5): 1573–1588. doi: 10.1007/s11128-014-0842-7

CARAIMAN S and MANTA V I. Image segmentation on a quantum computer[J]. Quantum Information Processing, 2015, 14(5): 1693–1715. doi: 10.1007/s11128-015-0932-1

JIANG Nan, ZHAO Na, and WANG Luo. LSB based quantum image steganography algorithm[J]. International Journal of Theoretical Physics, 2016, 55(1): 107–123. doi: 10.1007/s10773-015-2640-0

ZHOU Rigui, WU Qian, ZHANG Manqun, et al. Quantum image encryption and decryption algorithms based on quantum image geometric transformations[J]. International Journal of Theoretical Physics, 2013, 52(6): 1802–1817. doi: 10.1007/s10773-012-1274-8

LI Panchi, LIU Xiande, and XIAO Hong. Quantum image weighted average filtering in spatial domain[J]. International Journal of Theoretical Physics, 2017, 56(11): 3690–3716. doi: 10.1007/s10773-017-3533-1

魏春艳, 蔡晓秋, 王天银, 等. 基于量子不经意密钥传输的量子匿名认证密钥交换协议[J]. 电子与信息学报, 2020, 42(2): 341–347. doi: 10.11999/JEIT190679

WEI Chunyan, CAI Xiaoqiu, WANG Tianyin, et al. Quantum anonymous authenticated key exchange protocol based on quantum oblivious key transfer[J]. Journal of Electronics &Information Technology, 2020, 42(2): 341–347. doi: 10.11999/JEIT190679

倪博煜, 董晓阳. 改进的Type-1型广义Feistel结构的量子攻击及其在分组密码CAST-256上的应用[J]. 电子与信息学报, 2020, 42(2): 295–306. doi: 10.11999/JEIT190633

NI Boyu and DONG Xiaoyang. Improved quantum attack on type-1 generalized Feistel schemes and its application to CAST-256[J]. Journal of Electronics &Information Technology, 2020, 42(2): 295–306. doi: 10.11999/JEIT190633

ZHOU Rigui, HU Wenwen, FAN Ping, et al. Quantum color image watermarking based on Arnold transformation and LSB steganography[J]. International Journal of Quantum Information, 2018, 16(3): 1850021. doi: 10.1142/s0219749918500211

YUAN Suzhen, MAO Xuefen, ZHOU Jing, et al. Quantum image filtering in the spatial domain[J]. International Journal of Theoretical Physics, 2017, 56(8): 2495–2511. doi: 10.1007/s10773-017-3403-x

YUAN Suzhen, LU Yongle, MAO Xuefeng, et al. Improved quantum image filtering in the spatial domain[J]. International Journal of Theoretical Physics, 2018, 57(3): 804–813. doi: 10.1007/s10773-017-3614-1

LI Panchi, LIU Xiande, and XIAO Hong. Quantum image median filtering in the spatial domain[J]. Quantum Information Processing, 2018, 17(3): 49. doi: 10.1007/s11128-018-1826-9

王冬, 刘志昊, 朱皖宁, 等. 基于多目标扩展通用Toffoli门的量子比较器设计[J]. 计算机科学, 2012, 39(9): 302–306. doi: 10.3969/j.issn.1002-137X.2012.09.069

WANG Dong, LIU Zhihao, ZHU Wanning, et al. Design of quantum comparator based on extended general Toffoli gates with multiple targets[J]. Computer Science, 2012, 39(9): 302–306. doi: 10.3969/j.issn.1002-137X.2012.09.069

BENENTI G, CASATI C, and STRINI G, 王文阁, 李保文, 译. 量子计算与量子信息原理第一卷基本概念[M]. 北京: 科学出版社, 2011.

NIELSEN M A, CHUANG I L, 赵千川, 译. 量子计算和量子信息(一): 量子计算部分[M]. 北京: 清华大学出版社, 2004.

NIELSEN M A, CHUANG I L, ZHAO Qianchuan, translation. Quantum Computation and Quantum Information[M]. Beijing: Tsinghua Press, 2004.

HUNG W N N, SONG Xiaoyu, YANG Guowu, et al. Optimal synthesis of multiple output Boolean functions using a set of quantum gates by symbolic reachability analysis[J]. IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, 2006, 25(9): 1652–1663. doi: 10.1109/TCAD.2005.858352

施引文献

资源附件(0)

访问统计