Stagger Pulse Repetition Interval Pulse Train Deinterleaving Algorithm Based on Sequence Association
-
摘要: 针对复杂环境下常规直方图信号分选算法对于参差信号分选能力不佳的问题,该文提出一种基于脉冲间隔与单个脉冲关联的直方图算法。该算法根据脉冲间隔与单个脉冲的对应关系建立了脉冲间隔分布矩阵(PIDM),然后通过对PIDM行列的累加计算,得到一种新的直方图,该直方图可避免传统脉冲重复间隔(PRI)变换算法在分选参差信号时对于参差信号帧周期过多抑制的缺陷,且能够通过PIDM对辐射源脉冲串进行序列提取,进而得到参差子序列的周期值。仿真分析结果表明,在不增加计算复杂度的情况下,该算法对存在多部参差辐射源和固定重频辐射源的混合场景仍可保持良好的分选效果。Abstract: For the conventional histogram signal deinterleaving algorithm’s drawback of stagger signal, a histogram algorithm based on corresponding of pulse interval and single pulse is proposed. This algorithm utilizes the corresponding of pulse pair interval and single pulse to get a matrix named Pulse Interval Distribution Matrix (PIDM), and a novel histogram is obtained via cumulating row of the matrix. This histogram can avoid the suppressing of frame period of staggered pulse train caused by Pulse Repetition Intervals (PRI) transform algorithm when staggering signal deinterleaving, and can extract the subsequence of pulse train through PIDM. Simulation results show the algorithm has excellent performance on environment including multi staggered pulse trains with multi-fixed pulse trains under the circumstance of without adding the complexity of calculating.
-
表 1 不同信号环境下对比结果
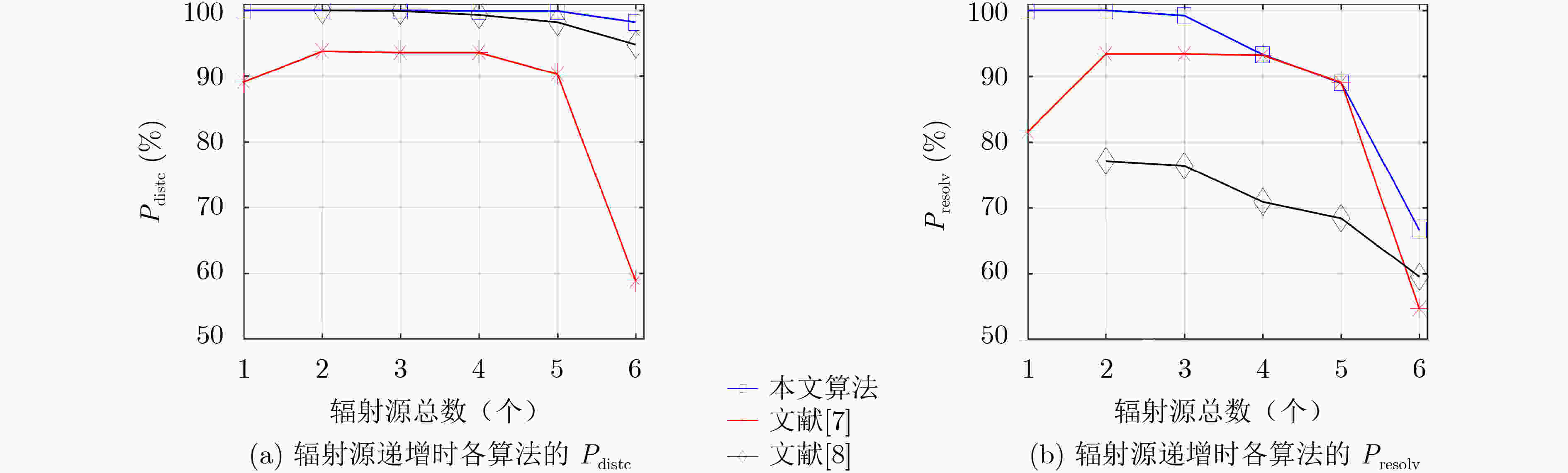
信号环境 ${P_{{\rm{resolv}}}}$ ${P_{{\rm{distc}}}}$ ${P_{{\rm{distcSTG}}}}$ 1参差信号 90.1/–/– 100/–/– 99.7/–/– 1参差1固定 89.5/93.4/85.7 100/93.4/85.7 98.2/–/– 1参差2固定 90.9/48.1/73.0 100/49.8/96.0 94.2/–/– 2参差2固定 82.7/18.4/70.8 98.6/20.2/94.8 91.3/–/– 2参差3固定 48.6/2.7/54.9 97.5/4.9/96.4 80.7/–/– 注:–表示所使用算法无该功能。 -
WILEY R G, 吕跃广, 全寿文, 王胜开, 等译. 电子情报(ELINT)——雷达信号截获与分析[M]. 北京: 电子工业出版社, 2008: 246–252.WILEY R G, LÜ Yueguang, QUAN Shouwen, WANG Shengkai, et al. translation. ELINT: The Interception and Analysis of Radar Signals[M]. Beijing: Publishing House of Electronics Industry, 2008: 246–252. 李合生, 韩宇, 蔡英武, 等. 雷达信号分选关键技术研究综述[J]. 系统工程与电子技术, 2005, 27(12): 2035–2040. doi: 10.3321/j.issn:1001-506X.2005.12.018LI Hesheng, HAN Yu, CAI Yingwu, et al. Overview of the crucial technology research for radar signal sorting[J]. Systems Engineering and Electronics, 2005, 27(12): 2035–2040. doi: 10.3321/j.issn:1001-506X.2005.12.018 吴惟诚, 潘继飞, 刘鑫, 等. 基于上升沿波形配对的信号分选方法研究[J]. 舰船电子工程, 2016, 36(12): 88–94, 100. doi: 10.3969/j.issn.1672-9730.2016.12.021WU Weicheng, PAN Jifei, LIU Xin, et al. Signal sorting method based on rising edge waveform matching[J]. Ship Electronic Engineering, 2016, 36(12): 88–94, 100. doi: 10.3969/j.issn.1672-9730.2016.12.021 张天骐, 张华伟, 刘董华, 等. 基于区域增长校正的频域盲源分离排序算法[J]. 电子与信息学报, 2019, 41(3): 580–587. doi: 10.11999/JEIT180386ZHANG Tianqi, ZHANG Huawei, LIU Donghua, et al. Frequency domain blind source separation permutation algorithm based on regional growth correction[J]. Journal of Electronics &Information Technology, 2019, 41(3): 580–587. doi: 10.11999/JEIT180386 MARDIA H K. New techniques for the deinterleaving of repetitive sequences[J]. IEE Proceedings F - Radar and Signal Processing, 1989, 136(4): 149–154. doi: 10.1049/ip-f-2.1989.0025 MILOJEVIC D J and POPOVIC B M. Improved algorithm for the deinterleaving of radar pulses[J]. IEE Proceedings F - Radar and Signal Processing, 1992, 139(1): 98–104. doi: 10.1049/ip-f-2.1992.0012 NISHIGUCHI K and KOBAYASHI M. Improved algorithm for estimating pulse repetition intervals[J]. IEEE Transactions on Aerospace and Electronic Systems, 2000, 36(2): 407–421. doi: 10.1109/7.845217 MAHDAVI A and PEZESHK A M. A fast enhanced algorithm of PRI transform[C]. The 6th International Symposium on Parallel Computing in Electrical Engineering, Luton, UK, 2011: 179–184. doi: 10.1109/PARELEC.2011.20. LIU Yanchao and ZHANG Qunying. Improved method for deinterleaving radar signals and estimating PRI values[J]. IET Radar, Sonar & Navigation, 2018, 12(5): 506–514. doi: 10.1049/iet-rsn.2017.0516 KOCAMIŞ M B, TORUN O, ABACI H, et al. Deinterleaving for radars with jitter and agile pulse repetition interval[C]. The 25th Signal Processing and Communications Applications Conference (SIU), Antalya, Turkey, 2017: 1–4. doi: 10.1109/SIU.2017.7960412. GE Zhipeng, SUN Xian, REN Wenjuan, et al. Improved algorithm of radar pulse repetition interval deinterleaving based on pulse correlation[J]. IEEE Access, 2019, 7: 30126–30134. doi: 10.1109/ACCESS.2019.2901013 关欣, 朱杭平. 基于序列时延相关性的PRI变换改进算法[J]. 雷达科学与技术, 2018, 16(1): 49–54. doi: 10.3969/j.issn.1672-2337.2018.01.008GUAN Xin and ZHU Hangping. An improved algorithm for PRI transform based on coherence of time delay sequence[J]. Radar Science and Technology, 2018, 16(1): 49–54. doi: 10.3969/j.issn.1672-2337.2018.01.008 陈涛, 王天航, 郭立民. 基于PRI变换的雷达脉冲序列搜索方法[J]. 系统工程与电子技术, 2017, 39(6): 1261–1267. doi: 10.3969/j.issn.1001-506X.2017.06.12CHEN Tao, WANG Tianhang, and GUO Limin. Sequence searching methods of radar signal pulses based on PRI transform algorithm[J]. Systems Engineering and Electronics, 2017, 39(6): 1261–1267. doi: 10.3969/j.issn.1001-506X.2017.06.12 李英达, 肖立志. 一种脉冲重复间隔复杂调制雷达信号分选方法[J]. 电子与信息学报, 2013, 35(10): 2493–2497. doi: 10.3724/SP.J.1146.2013.00060LI Yingda and XIAO Lizhi. A method of signal sorting for radar signal of pulse repetition interval complex modulated[J]. Journal of Electronics &Information Technology, 2013, 35(10): 2493–2497. doi: 10.3724/SP.J.1146.2013.00060 柳征, 高超, 李悦. 基于数据关联处理的重频参差雷达信号分选方法[J]. 电子与信息学报, 2018, 40(5): 1130–1135. doi: 10.11999/JEIT170793LIU Zheng, GAO Chao, and LI Yue. Signal sorting algorithm for stagger pulse repetition interval radar based on data association processing[J]. Journal of Electronics &Information Technology, 2018, 40(5): 1130–1135. doi: 10.11999/JEIT170793 SHAHHOSEINI H S, NASERI A, and NADERI M. A new matrix method for pulse train identification: Implementing by systolic array[C]. The 11th European Signal Processing Conference, Toulouse, France, 2002: 1–4. -






 下载:
下载:



 下载:
下载:
