基于稀疏感知有序干扰消除的大规模机器类通信系统多用户检测

申滨; 吴和彪; 赵书锋; 崔太平

doi:10.11999/JEIT190994

基于稀疏感知有序干扰消除的大规模机器类通信系统多用户检测

doi: 10.11999/JEIT190994

重庆邮电大学通信与信息工程学院重庆 400065

基金项目: 国家重大研发计划(2017YFE0118900)，欧盟H2020项目(734798)

详细信息

作者简介:
申滨：男，1978年生，教授，研究方向为认知无线电、大规模MIMO等

吴和彪：男，1994年生，硕士生，研究方向为大规模机器类系统多用户检测

赵书锋：男，1991年生，硕士生，研究方向为大规模MIMO系统信号检测

崔太平：男，1981年生，讲师，研究方向为认知无线电、车联网

通讯作者:
申滨　shenbin@cqupt.edu.cn

中图分类号: TN929.5
计量
- 文章访问数: 1593
- HTML全文浏览量: 540
- PDF下载量: 58
- 被引次数: 0
出版历程
- 收稿日期: 2019-12-13
- 修回日期: 2020-06-23
- 网络出版日期: 2020-07-18
- 刊出日期: 2020-12-08

Sparsity-aware Ordered Successive Interference Cancellation Based Multi-user Detection for Uplink mMTC

School of Communications and Information Engineering, Chongqing University of Posts andTelecommunications, Chongqing 400065, China

Funds: The National Key R&D Program of China (2017YFE0118900), The EU H2020 Project (734798)

摘要

摘要:
在大规模机器类通信(mMTC)系统中，以用户活跃性为先验信息，接收机可以基于稀疏感知最大后验概率(S-MAP)准则来检测多用户信号。为了降低S-MAP检测的计算复杂度，基于干扰消除的思想，该文提出一种改进的活跃性感知有序正交三角分解(IA-SQRD)算法，以适用于mMTC系统上行链路多用户信号检测。IA-SQRD算法将传统的活跃性感知有序正交三角分解(A-SQRD)算法的最终解作为初始解，并额外增加迭代干扰消除操作，以进一步提高检测性能。此外，利用与改进A-SQRD算法相似的思路，该文对稀疏感知串行干扰消除(SA-SIC)、有序正交三角分解(SQRD)及数据相关的排序和正则化(DDS)算法亦进行了改进设计，分别获得了相应的改进型算法，即ISA-SIC、I-SQRD及I-DDS算法。仿真结果表明：相对于A-SQRD算法，在未显著增加计算复杂度的情况下，在系统误比特率(BER)为
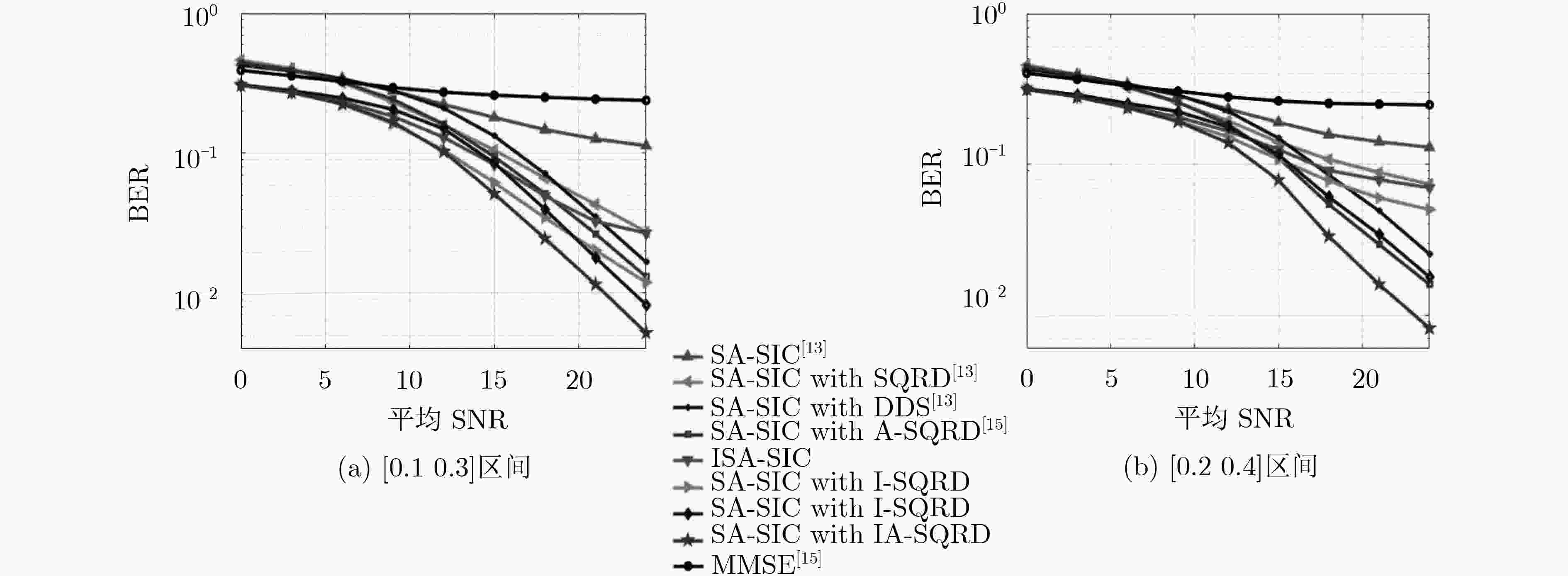
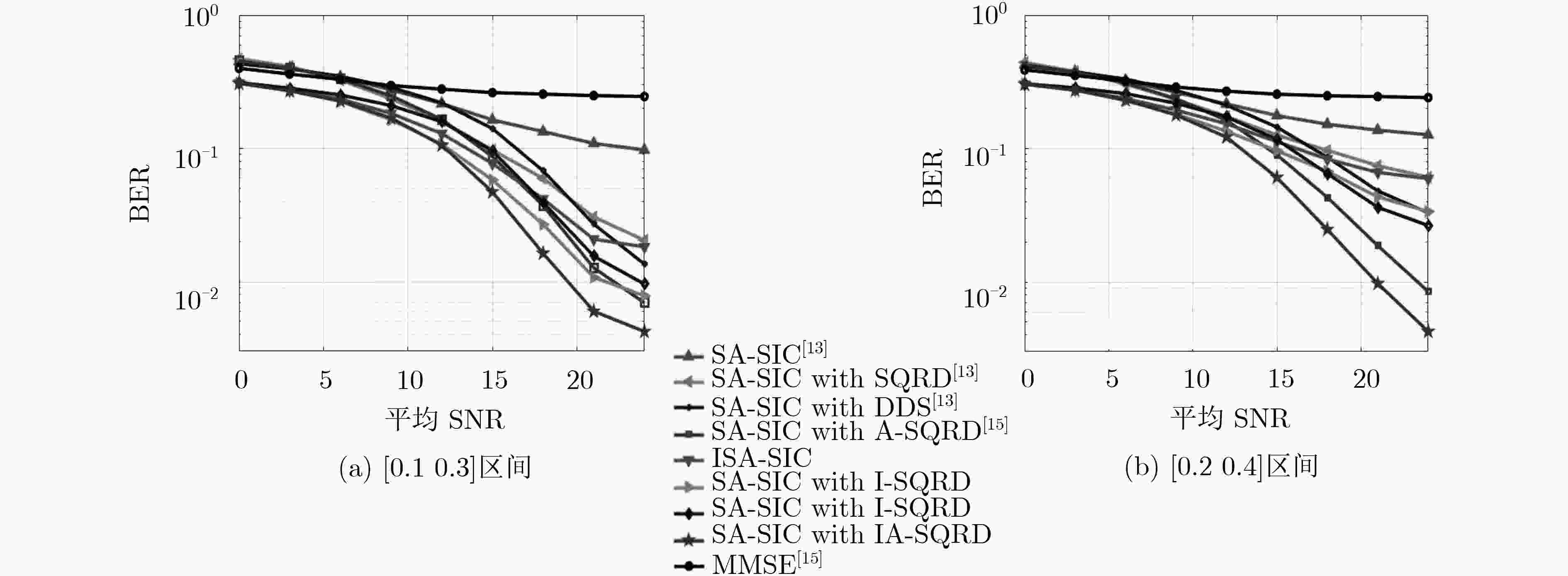
\begin{document}$2.5 \times {10^{ - 2}}$\end{document}
时，该文所提IA-SQRD算法可取得3 dB性能增益；并且，对于不同的活跃概率或扩频序列长度等参数配置下的mMTC系统，IA-SQRD算法相对于其它算法均表现出更优良的多用户检测性能。
- 多用户检测 /
- 大规模机器类通信 /
- 最大后验概率 /
- 串行干扰消除
Abstract:
In massive Machine-Type Communication (mMTC) systems, when the user activity is exploited as a priori information for the receiver, the Sparsity-aware Maximum A Posteriori probability (S-MAP) criterion can be used to recover the sparse multi-user vectors over the uplink mMTC systems. In order to reduce the computational complexity of S-MAP detection, based on interference cancellation mechanism, an Improved Activity-aware Sorted QR Decomposition (IA-SQRD) algorithm is proposed in this paper. The IA-SQRD algorithm utilizes the final solution of the A-SQRD algorithm as the initial solution and the iterative interference cancellation operation is performed to improve further the detection performance. Following the same philosophy in improving the A-SQRD algorithm, the conventional Sparsity-Aware Successive Interference Cancellation (SA-SIC), Sorted QR Decomposition (SQRD), and Data-Dependent Sorting and regularization (DDS) algorithms are modified to enhance the performance, respectively. Simulation results verify that compared with the A-SQRD algorithm, a 3 dB gain is achieved by the proposed IA-SQRD algorithm when the Bit Error Rate (BER) is
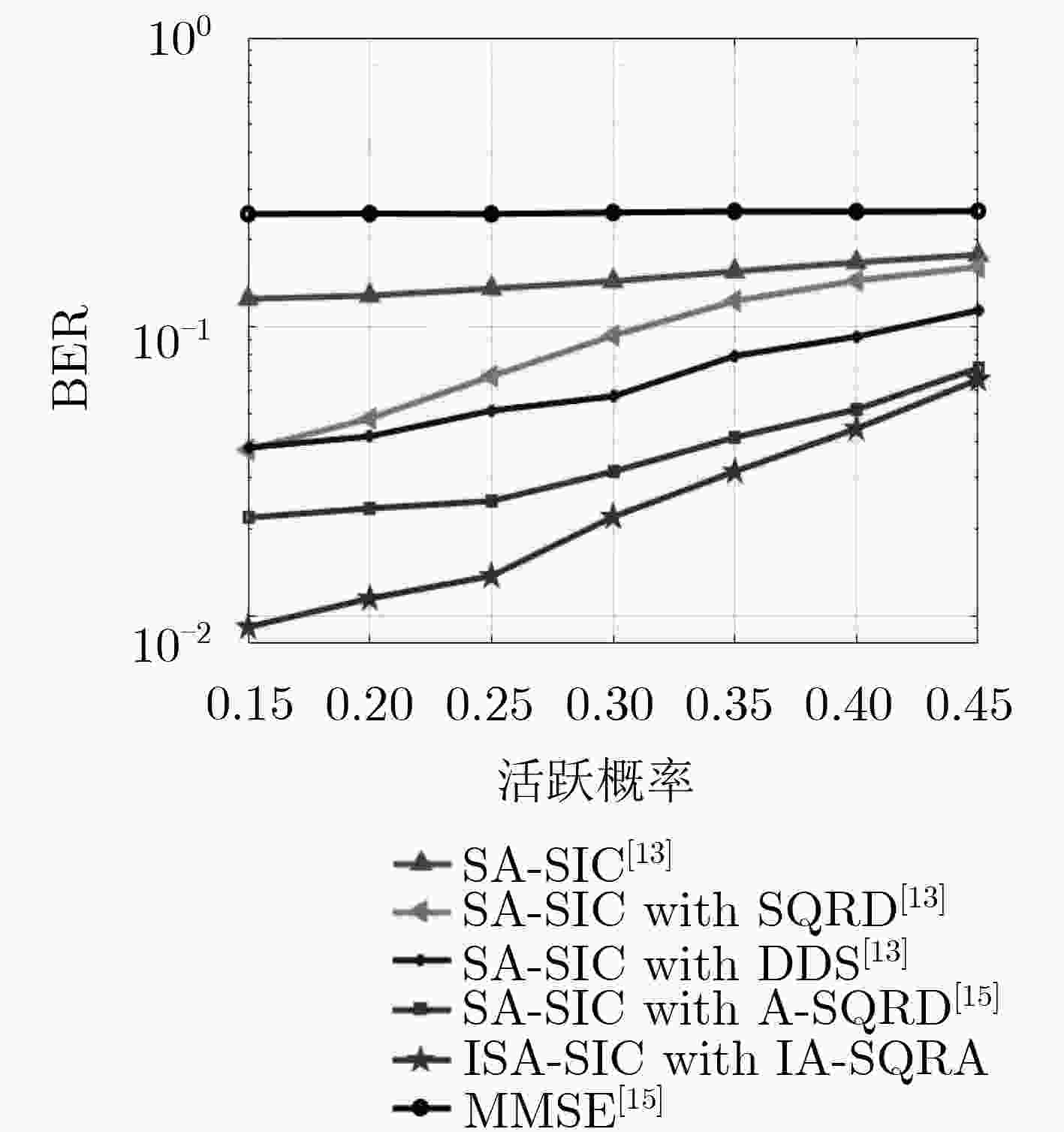
\begin{document}$2.5 \times {10^{ - 2}}$\end{document}
, without significantly increasing the computational complexity. In addition, given different system configurations in terms of active probability and the length of spread spectrum sequence, the proposed IA-SQRD also exhibits better performance than that of the other algorithms mentioned in this paper.
- Multi-user detection /
- Massive Machine-Type Communication (mMTC) /
- Maximum A Posteriori (MAP) probability /
- Successive interference cancellation

HTML全文

图 1 在[0.1 0.3]区间中随机均匀分布的用户活跃概率

下载: 全尺寸图片幻灯片

图 2 BER性能对比，$64 \times 128$配置

下载: 全尺寸图片幻灯片

图 3 BER性能对比，$128 \times 256$配置

下载: 全尺寸图片幻灯片

图 4 不同用户活跃概率对应的BER性能

下载: 全尺寸图片幻灯片

图 5 不同扩频序列长度对应的BER性能

下载: 全尺寸图片幻灯片

表 1 改进型活跃性感知有序正交三角分解(IA-SQRD)检测算法

　输入：${y}$, ${H}$, ${{A}_0}$, ${\rm{\sigma }}_w^2$,$\left\{ {{p_n}} \right\}_{n = 1}^N$

　输出：${{\bar s}^{{T_{{\rm{iter}}}}}}$(${T_{{\rm{iter}}}}$为迭代次数)

　(1) ${{\rm{\lambda }}_n} = \ln [(1 - {p_n})/({p_n}/\left| {A} \right|)]$

　(2) ${{y}_0} = [{y};{\bf{0}_N}]$, ${Q} = [{H};{{\rm{\sigma }}_w}{\rm{diag}}\left( {\sqrt {{\lambda }} } \right)]$, ${R} = {{{\textit{0}}}_{N \times N}}$, ${P} = {{I}_N}$

　(3) for $n = 1,2, \cdots ,N$ do

　(4) ${n_{\min } } = \arg {\min _{j = n,n + 1, ··· ,N} }{\left\| { {{q}_j} } \right\|^2}$

　(5) 交换${Q}$, ${R}$和${P}$中的$n$和${n_{\min }}$列

　(6) ${R_{nn}} = \left\| {{{q}_n}} \right\|$,${{q}_n} = {{q}_n}/{R_{nn}}$

　(7) for $j = n + 1, ···,N - 1,N$ do

　(8) ${R_{nj}} = {q}_n^{\rm{H}}{{q}_j}$, ${{q}_j} = {{q}_j} - {R_{nj}}{{q}_n}$

　(9) end for

　(10) end for

　(11) ${{\tilde y}_0} = {{Q}^{\rm{H}}}{{y}_0}$

　(12) for $n = N,N - 1, ··· ,1$ do

　(13) $x_n' = \left({\tilde y_{0,n} } - \displaystyle\sum\limits_{l = n + 1}^N { {R_{nl} } } {\hat x_l}\right)/{R_{nn} }$

　(14) ${\hat x_n} = {Q_{{{A}_0}}}({x_{n'}})$

　(15) end for

　(16) $\hat{ x} = \hat{ x}{{P}^{\rm{H}}}$

　(17) ${s} = \hat{ x}$

　(18) ${G} = {{H}^{\rm{H}}}{H}$, ${b} = {{H}^{\rm{H}}}{y}$

　(19) for $t = 1:{T_{{\rm{iter}}}}$

　(20) for $n = 1:N$
　(21) $\hat s_n^{(t)} = \hat s_n^{(t - 1)} + \dfrac{ { {b_n} - \displaystyle\sum\limits_{j = 1}^N { {G_{nj} }\hat s_j^{(t - 1)} } } }{ { {G_{nn} } } }$

　(22) $\bar s_n^{(t)} = {Q_{{{A}_0}}}(\hat s_n^{(t)})$

　(23) end for

　(24) end for

下载: 导出CSV

表 2 计算复杂度比较(复数浮点运算次数)

$M$	$N$	SQRD	A-SQRD	I-SQRD	IA-SQRD
$16$	$32$	$3.4 \times {10^4}$	$1.0 \times {10^5}$	$5.5 \times {10^4}$	$1.2 \times {10^5}$
$32$	$64$	$2.7 \times {10^5}$	$7.9 \times {10^5}$	$4.2 \times {10^5}$	$9.4 \times {10^5}$
$64$	$128$	$2.1 \times {10^6}$	$6.3 \times {10^6}$	$3.2 \times {10^6}$	$7.4 \times {10^6}$

下载: 导出CSV

参考文献(21)

DAWY Z, SAAD W, GHOSH A, et al. Toward massive machine type cellular communications[J]. IEEE Wireless Communications, 2017, 24(1): 120–128. doi: 10.1109/MWC.2016.1500284WC

GHAVIMI F and CHEN H H. M2M communications in 3GPP LTE/LTE-A networks: Architectures, service requirements, challenges, and applications[J]. IEEE Communications Surveys & Tutorials, 2015, 17(2): 525–549. doi: 10.1109/COMST.2014.2361626

SHIM B and SONG B. Multiuser detection via compressive sensing[J]. IEEE Communications Letters, 2012, 16(7): 972–974. doi: 10.1109/LCOMM.2012.050112.111980

CHOI J W, SHIM B, DING Yacong, et al. Compressed sensing for wireless communications: useful tips and tricks[J]. IEEE Communications Surveys & Tutorials, 2017, 19(3): 1527–1550. doi: 10.1109/COMST.2017.2664421

ZHU Hao and GIANNAKIS G B. Exploiting sparse user activity in multiuser detection[J]. IEEE Transactions on Communications, 2011, 59(2): 454–465. doi: 10.1109/TCOMM.2011.121410.090570

BARIK S and VIKALO H. Sparsity-aware sphere decoding: algorithms and complexity analysis[J]. IEEE Transactions on Signal Processing, 2014, 62(9): 2212–2225. doi: 10.1109/TSP.2014.2307836

KNOOP B, MONSEES F, BOCKELMANN C, et al. Compressed sensing K-best detection for sparse multi-user communications[C]. The 22nd European Signal Processing Conference, Lisbon, Portugal, 2014: 1726–1730.

ZHANG Xiaoxu, LIANG Yingchang, and FANG Jun. Novel Bayesian inference algorithms for multiuser detection in M2M communications[J]. IEEE Transactions on Vehicular Technology, 2017, 66(9): 7833–7848. doi: 10.1109/TVT.2017.2692776

ZHANG Xiaoxu, LABEAU F, LIANG Yingchang, et al. Compressive sensing-based multiuser detection via iterative reweighed approach in M2M communications[J]. IEEE Wireless Communications Letters, 2018, 7(5): 764–767. doi: 10.1109/LWC.2018.2820704

JEONG B K, SHIM B, and LEE K B. MAP-based active user and data detection for massive machine-type communications[J]. IEEE Transactions on Vehicular Technology, 2018, 67(9): 8481–8494. doi: 10.1109/TVT.2018.2849621

DI RENNA R B and DE LAMARE R C. Activity-aware multiple feedback SIC for massive machine-type communications[C]. The 12th International ITG Conference on Systems, Communications and Coding, Rostock, Germany, 2019: 233–238.

丁子哲, 张贤达. 基于串行干扰消除的V-BLAST检测[J]. 电子学报, 2007, 35(S1): 19–24.

DING Zizhe and ZHANG Xianda. V-BLAST detection based on successive interference cancellation[J]. Acta Electronica Sinica, 2007, 35(S1): 19–24.

KNOOP B, MONSEES F, BOCKELMANN C, et al. Sparsity-aware successive interference cancellation with practical constraints[C]. The 17th International ITG Workshop on Smart Antennas, Stuttgart, Germany, 2013: 1–8.

LIU Yi, YUEN C, CAO Xianghui, et al. Design of a scalable hybrid MAC protocol for heterogeneous M2M networks[J]. IEEE Internet of Things Journal, 2014, 1(1): 99–111. doi: 10.1109/JIOT.2014.2310425

AHN J, SHIM B, and LEE K B. Sparsity-aware ordered successive interference cancellation for massive machine-type communications[J]. IEEE Wireless Communications Letters, 2018, 7(1): 134–137. doi: 10.1109/LWC.2017.2760831

YANG Zhaohui, CHEN Ming, PAN Yijin, et al. Asynchronous detection for machine-to-machine systems with code division multiple access[C]. The 9th International Conference on Wireless Communications and Signal Processing, Nanjing, China, 2017.

YANG Zhaohui, CHEN Ming, WANG Yinlu, et al. Compressive sensing based multiuser detection for asynchronous machine-to-machine systems[C]. The 9th International Conference on Wireless Communications and Signal Processing, Nanjing, China, 2017.

BJÖRCK Å. Numerics of gram-schmidt orthogonalization[J]. Linear Algebra and Its Applications, 1994, 197/198: 297–316. doi: 10.1016/0024-3795(94)90493-6

MANDLOI M and BHATIA V. Low-complexity near-optimal iterative sequential detection for uplink massive MIMO systems[J]. IEEE Communications Letters, 2017, 21(3): 568–571. doi: 10.1109/LCOMM.2016.2637366

申滨, 吴和彪, 崔太平, 等. 基于最优索引广义正交匹配追踪的非正交多址系统多用户检测[J]. 电子与信息学报, 2020, 42(3): 621–628. doi: 10.11999/JEIT190270

SHEN Bin, WU Hebiao, CUI Taiping, et al. An optimal number of indices aided gOMP algorithm for multi-user detection in NOMA system[J]. Journal of Electronics &Information Technology, 2020, 42(3): 621–628. doi: 10.11999/JEIT190270

申滨, 赵书锋, 金纯. 基于迭代并行干扰消除的低复杂度大规模MIMO信号检测算法[J]. 电子与信息学报, 2018, 40(12): 2970–2978. doi: 10.11999/JEIT180111

SHEN Bin, ZHAO Shufeng, and JIN Chun. Low complexity iterative parallel interference cancellation detection algorithms for massive MIMO systems[J]. Journal of Electronics &Information Technology, 2018, 40(12): 2970–2978. doi: 10.11999/JEIT180111

施引文献

资源附件(0)

访问统计