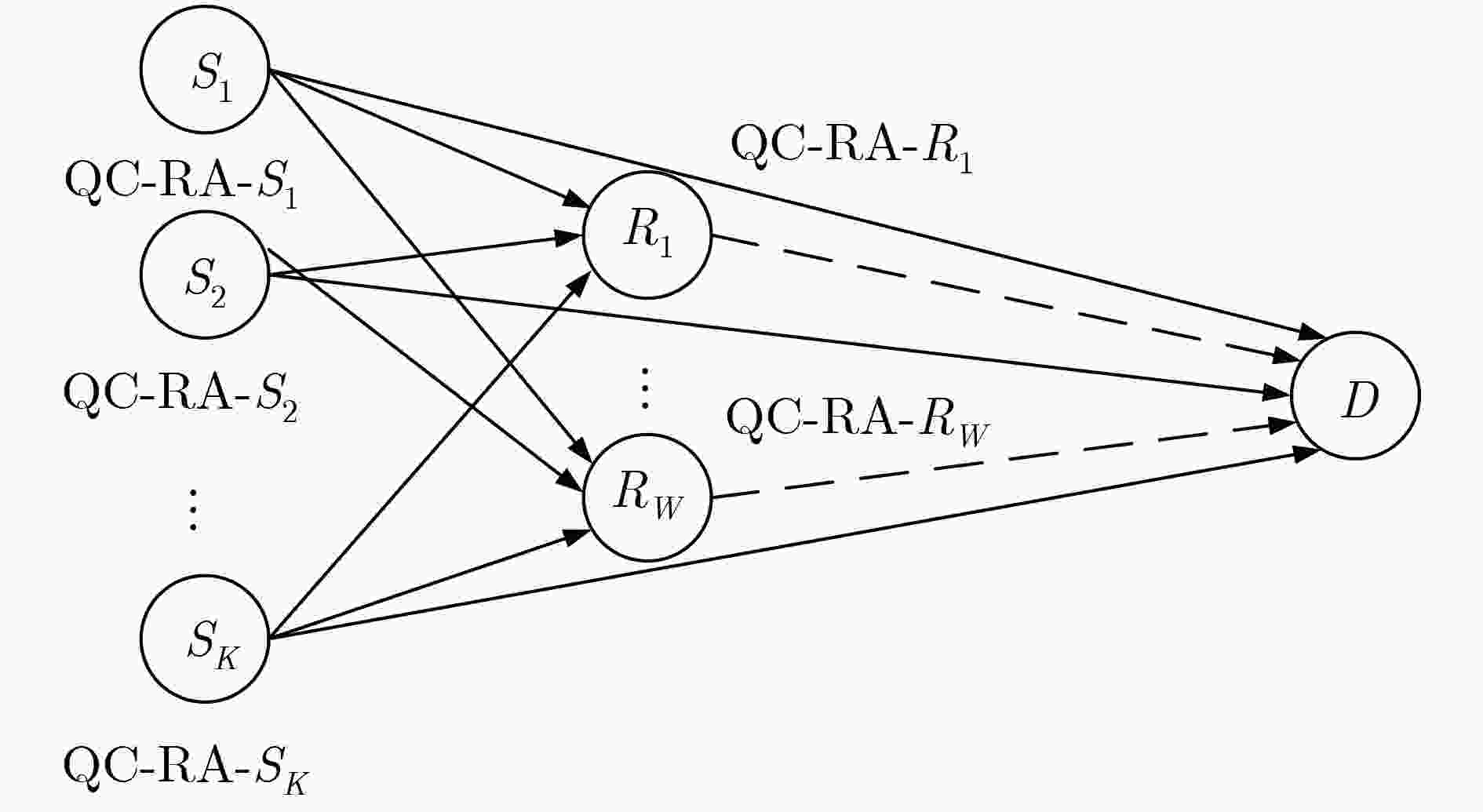
Joint Design of QC-RA Codes and Performance Analysis of Coded Cooperation
-
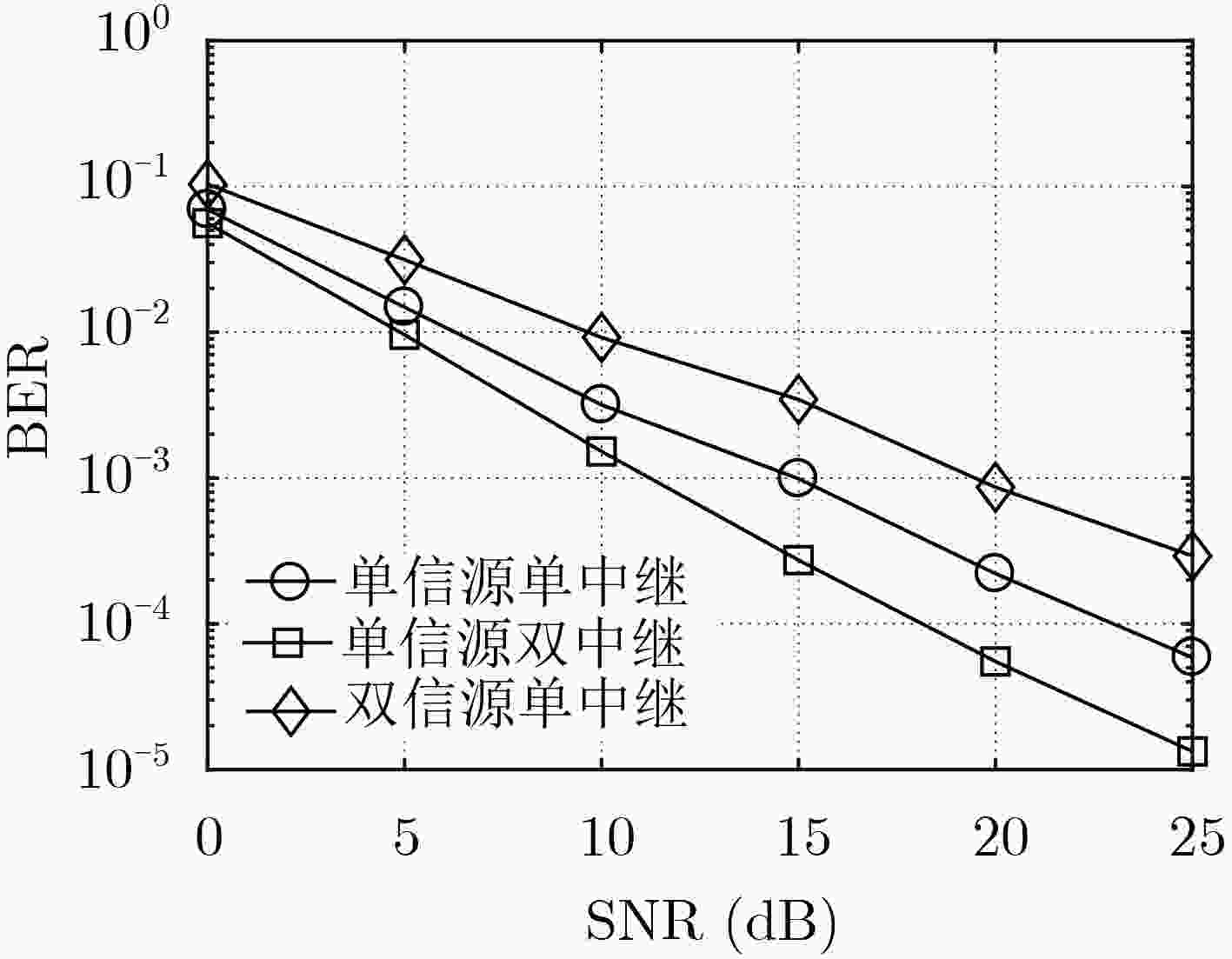
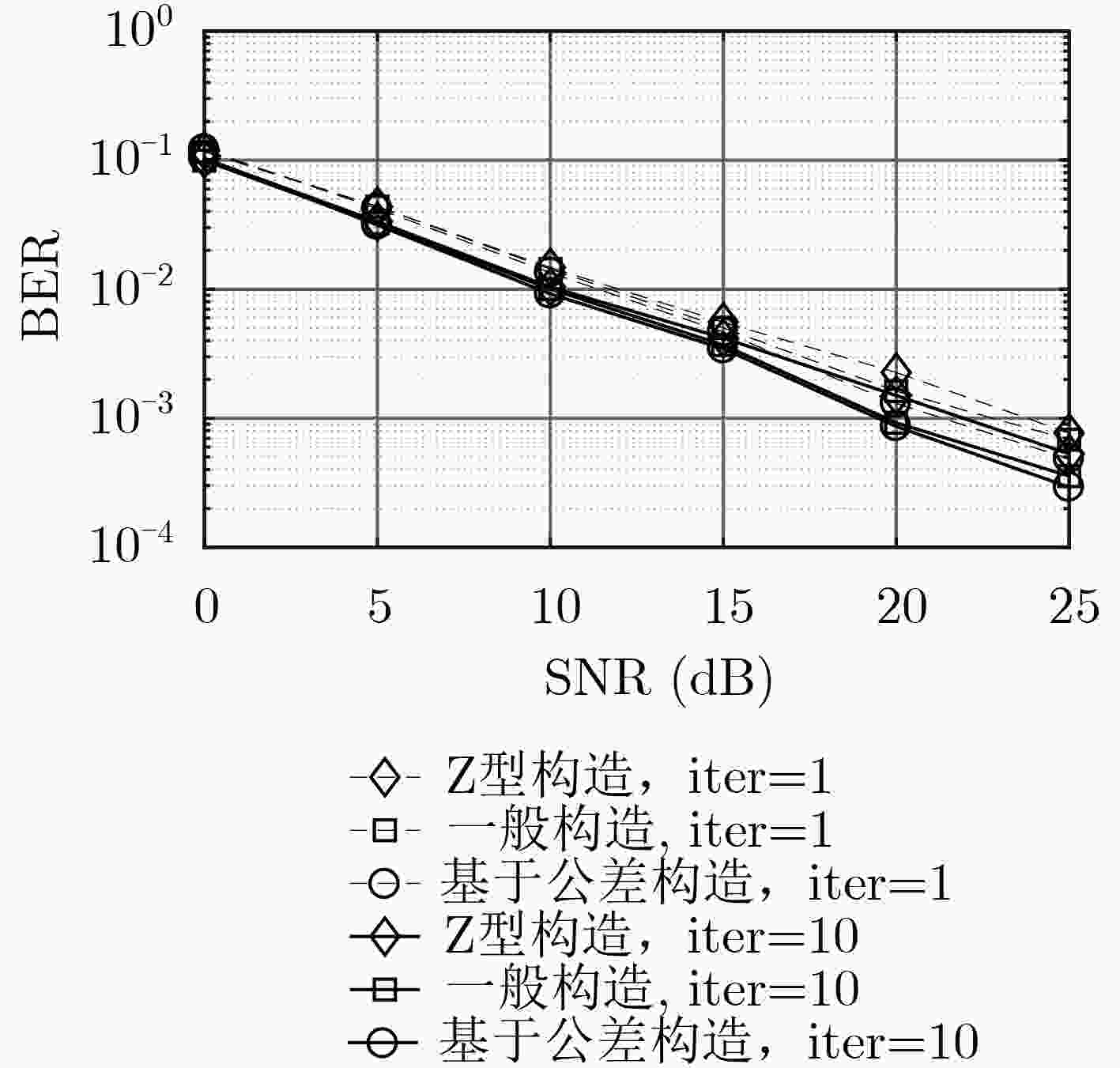
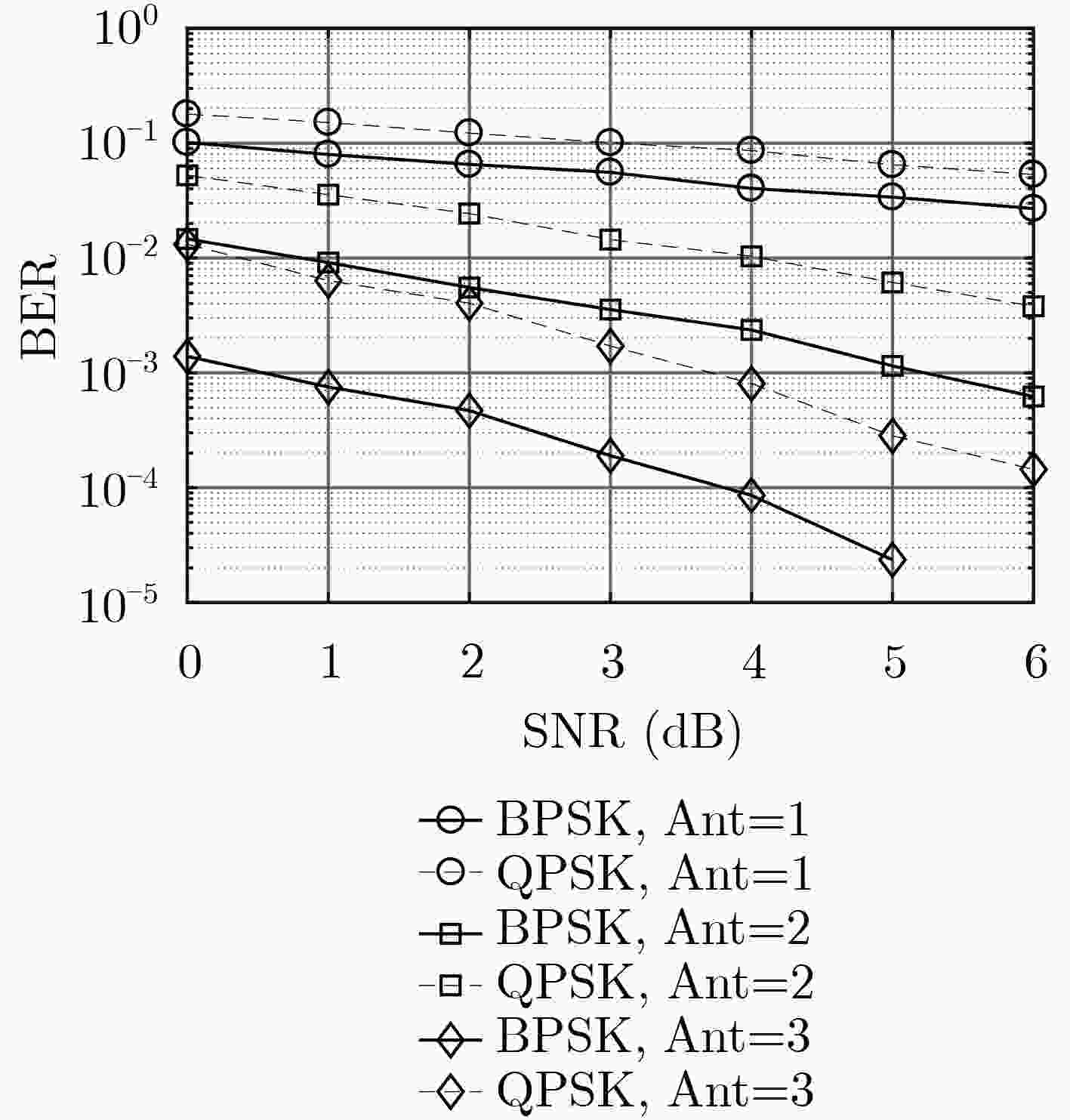
摘要: 重复累积(RA)码是一种特殊结构的低密度奇偶校验(LDPC)码,不仅具有LDPC码的优点,还能实现差分编码。针对LDPC编码协作系统编码复杂度高、时延长的问题,该文引入准循环RA(QC-RA)码,推导出信源节点和中继节点采用的QC-RA码对应的联合校验矩阵,基于公差构造方法设计该联合校验矩阵,并证明该方法设计的联合校验矩阵不存在围长为girth-4, girth-6的短环。理论分析和仿真结果表明,同等条件下该系统比相应点对点系统具有更优异的误码率性能。仿真结果同时表明,与采用一般构造QC-RA码或基于Z型构造QC-RA码相比,采用基于公差构造的联合设计QC-RA码的多信源多中继协作均可获得更高的编码增益。Abstract: Repeat Accumulate (RA) code is a special kind of Low Density Parity Check (LDPC) code, which not only has the advantages of LDPC code, but also realizes differential encoding. To solve the problems of high encoding complexity and long encoding delay of LDPC-coded cooperative system, Quasi-Cyclic RA (QC-RA) code is introduced. Firstly, a joint parity check matrix corresponding to the QC-RA codes adopted by the sources and relays is deduced; Secondly, the joint check matrix is designed based on the Common Difference Construction (CDC) method, and it is proved that the joint check matrix designed by the CDC method does not have short cycles with girth-4 or girth-6. Theoretical analysis and simulation results show that the system achieves better Bit Error Rate (BER) performance than the corresponding point-to-point system under the same conditions. The simulation results also demonstrate that the multi-source multi-relay coded cooperation with CDC constructed QC-RA code can obtain higher coding gain than that with generally constructed QC-RA code or Z-type constructed QC-RA code.
-
表 1 双信源双中继编码协作及对应点对点系统采用的QC-RA码
信源节点采用的QC-RA码 中继节点采用的QC-RA码 双信源双中继
编码协作系统$\begin{array}{l} {{{H}}_{{S_1}}} = \left[ {\begin{array}{*{20}{c}} {{{A}}_{(1700 \times 850)}^{(1)}}&{{{{D}}_{(1700 \times 1700)}}} \end{array}} \right] \\ {{{H}}_{{S_2}}} = \left[ {\begin{array}{*{20}{c}} {{{A}}_{(1700 \times 850)}^{(2)}}&{{{{D}}_{(1700 \times 1700)}}} \end{array}} \right] \end{array} $
Rate=1/3$\begin{array}{l} {{{H}}_{{R_1}}} = \left[ {\begin{array}{*{20}{c}} {{{B}}_{1(1700 \times 850)}^{(1)}}&{{{B}}_{2(1700 \times 850)}^{(1)}}&{{{{D}}_{(1700 \times 1700)}}} \end{array}} \right] \\ {{{H}}_{{R_2}}} = \left[ {\begin{array}{*{20}{c}} {{{B}}_{1(1700 \times 850)}^{(2)}}&{{{B}}_{2(1700 \times 850)}^{(2)}}&{{{{D}}_{(1700 \times 1700)}}} \end{array}} \right] \end{array} $
Rate=3/4点对点系统 ${{{H}}_S} = \left[ {\begin{array}{*{20}{c}} {{{{H}}_{(6800 \times 1700)}}}&{{{{D}}_{(6800 \times 6800)}}} \end{array}} \right]$ Rate=1/5 \ 表 2 不同信源节点、中继节点数目情况下编码协作系统采用的RA码
信源节点采用的QC-RA码 中继节点采用的QC-RA码 双信源单中继系统 $\begin{array}{l} {{{H}}_{{S_1}}} = \left[ {\begin{array}{*{20}{c}} {{{A}}_{(1700 \times 1700)}^{(1)}}&{{{{D}}_{(1700 \times 1700)}}} \end{array}} \right] \\ {{{H}}_{{S_2}}} = \left[ {\begin{array}{*{20}{c}} {{{A}}_{(1700 \times 1700)}^{(2)}}&{{{{D}}_{(1700 \times 1700)}}} \end{array}} \right] \end{array} $
Rate=1/2${{{H}}_R} = \left[ {\begin{array}{*{20}{c}} {{{{B}}_{1(1700 \times 1700)}}}&{{{{B}}_{2(1700 \times 1700)}}}&{{{{D}}_{(1700 \times 1700)}}} \end{array}} \right]$
Rate=2/3单信源双中继系统 ${{{H}}_S} = \left[ {\begin{array}{*{20}{c}} {{{{A}}_{(1700 \times 1700)}}}&{{{{D}}_{(1700 \times 1700)}}} \end{array}} \right]$
Rate=1/2$\begin{array}{l} {{{H}}_{{R_1}}} = \left[ {\begin{array}{*{20}{c}} {{{B}}_{(1700 \times 1700)}^{(1)}}&{{{{D}}_{(1700 \times 1700)}}} \end{array}} \right] \\ {{{H}}_{{R_2}}} = \left[ {\begin{array}{*{20}{c}} {{{B}}_{(1700 \times 1700)}^{(2)}}&{{{{D}}_{(1700 \times 1700)}}} \end{array}} \right] \end{array} $
Rate=1/2单信源单中继系统 ${{{H}}_S} = \left[ {\begin{array}{*{20}{c}} {{{{A}}_{(1700 \times 1700)}}}&{{{{D}}_{(1700 \times 1700)}}} \end{array}} \right]$
Rate=1/2${{{H}}_R} = \left[ {\begin{array}{*{20}{c}} {{{{B}}_{(1700 \times 1700)}}}&{{{{D}}_{(1700 \times 1700)}}} \end{array}} \right]$
Rate=1/2 -
[1] GALLAGER R G. Low-Density Parity-Check Codes[M]. Cambridge: The MIT Press, 1963. [2] CHEN Weigang, HAN Changcai, and YANG Jinsheng. Low-complexity encoder for LDPC codes in space applications[J]. Electronics Letters, 2019, 55(23): 1241–1243. doi: 10.1049/el.2019.2417 [3] VATTA F, SORANZO A, COMISSO M, et al. Performance study of a class of irregular LDPC codes through low complexity bounds on their belief-propagation decoding thresholds[C]. 2019 AEIT International Annual Conference (AEIT), Florence, Italy, 2019: 1–6. doi: 10.23919/AEIT.2019.8893306. [4] TASDIGHI A, BANIHASHEMI A H, and SADEGHI M R. Symmetrical constructions for regular girth-8 QC-LDPC codes[J]. IEEE Transactions on Communications, 2017, 65(1): 14–22. doi: 10.1109/TCOMM.2016.2617335 [5] LI Jialiang, CHEN Wen, JIANG Xueqin, et al. Construction of multiple-rate quasi-cyclic LDPC codes with girth eight[C]. 2016 8th International Conference on Wireless Communications & Signal Processing, Yangzhou, China, 2016: 1–5. doi: 10.1109/WCSP.2016.7752486. [6] 张轶, 达新宇, 苏一栋. 利用等差数列构造大围长准循环低密度奇偶校验码[J]. 电子与信息学报, 2015, 37(2): 394–398. doi: 10.11999/JEIT140538ZHANG Yi, DA Xinyu, and SU Yidong. Construction of quasi-cyclic low-density parity-check codes with a large girth based on arithmetic progression[J]. Journal of Electronics &Information Technology, 2015, 37(2): 394–398. doi: 10.11999/JEIT140538 [7] ZHANG Yi and DA Xinyu. Construction of girth-eight QC-LDPC codes from arithmetic progression sequence with large column weight[J]. Electronics Letters, 2015, 51(16): 1257–1259. doi: 10.1049/el.2015.0389 [8] ZHANG Guohua, SUN Rong, and WANG Xinmei. Construction of girth-eight QC-LDPC codes from greatest common divisor[J]. IEEE Communications Letters, 2013, 17(2): 369–372. doi: 10.1109/LCOMM.2012.122012.122292 [9] SUN Rong, LIU Jingwei, ZHANG Pingli, et al. On the rateless character of irregular RA codes[C]. 2011 IEEE Workshops of International Conference on Advanced Information Networking and Applications, Singapore, 2011: 297–301. doi: 10.1109/WAINA.2011.49. [10] LANEMAN J N, WORNELL G W, and TSE D N C. An efficient protocol for realizing cooperative diversity in wireless networks[C]. 2001 IEEE International Symposium on Information Theory, Washington, USA, 2001: 294–295. doi: 10.1109/ISIT.2001.936157. [11] VAN NGUYEN B, JUNG H, and KIM K. Physical layer security schemes for full-duplex cooperative systems: State of the art and beyond[J]. IEEE Communications Magazine, 2018, 56(11): 131–137. doi: 10.1109/MCOM.2017.1700588 [12] WANG Jieling, YU Quan, LI Zan, et al. Distributed space time block transmission and QRD based diversity detector in asynchronous cooperative communications systems[J]. IEEE Transactions on Vehicular Technology, 2018, 67(6): 5111–5125. doi: 10.1109/TVT.2018.2812901 [13] MOUALEU J M, HAMOUDA W, XU Hongjun, et al. Multi-relay turbo-coded cooperative diversity networks over Nakagami-m fading channels[J]. IEEE Transactions on Vehicular Technology, 2013, 62(9): 4458–4470. doi: 10.1109/TVT.2013.2265329 [14] EJAZ S and YANG Fengfan. Jointly optimized Reed-Muller codes for multilevel multirelay coded-cooperative VANETS[J]. IEEE Transactions on Vehicular Technology, 2017, 66(5): 4017–4028. doi: 10.1109/TVT.2016.2604320 [15] SHIRVANIMOGHADDAM M, LI Yonghui, TIAN Shuang, et al. Distributed raptor coding for erasure channels: Partially and fully coded cooperation[J]. IEEE Transactions on Communications, 2013, 61(9): 3576–3589. doi: 10.1109/TCOMM.2013.072913.120724 [16] JIN Ming, WANG Junming, ZHANG Yan, et al. The research and design of single relay coded cooperative system based on Polar codes[C]. 2017 13th IEEE International Conference on Electronic Measurement & Instruments, Yangzhou, China, 2017: 254–258. doi: 10.1109/ICEMI.2017.8265949. [17] WANG Hui and CHEN Qingchun. LDPC based network coded cooperation design for multi-way relay networks[J]. IEEE Access, 2019, 7: 62300–62311. doi: 10.1109/ACCESS.2019.2915293 [18] 张顺外. LDPC编码协作系统性能与码的设计研究[D]. [博士学位论文], 南京航空航天大学, 2013.ZHANG Shunwai. LDPC-coded cooperation: Performance studies and codes design[D]. [Ph.D. dissertation], Nanjing University of Aeronautics and Astronautics, 2013. [19] 张顺外, 魏琪. 多信源多中继编码协作系统准循环LDPC码的联合设计与性能分析[J]. 电子与信息学报, 2019, 41(10): 2325–2333. doi: 10.11999/JEIT190069ZHANG Shunwai and WEI Qi. Joint design of quasi-cyclic low density parity check codes and performance analysis of multi-source multi-relay coded cooperative system[J]. Journal of Electronics &Information Technology, 2019, 41(10): 2325–2333. doi: 10.11999/JEIT190069 [20] ZHANG Shunwai, YANG Fengfan, TANG Lei, et al. Network-coding-based multisource RA-coded cooperative MIMO[C]. 2013 3rd International Conference on Computer Science and Network Technology, Dalian, China, 2013: 737–741. doi: 10.1109/ICCSNT.2013.6967215. [21] SADEGHI M R. Optimal search for girth-8 quasi cyclic and spatially coupled multiple-edge LDPC codes[J]. IEEE Communications Letters, 2019, 23(9): 1466–1469. doi: 10.1109/LCOMM.2019.2924892 [22] ZHANG Shunwai, YANG Fengfan, and SONG Rongfang. Energy-harvesting-based RA-coded cooperative MIMO: Codes design and performance analysis[J]. Digital Signal Processing, 2017, 60: 56–62. doi: 10.1016/j.dsp.2016.08.013 [23] RYAN W E and LIN Shu. Channel Codes Classical and Modern[M]. Cambridge, UK: Cambridge University Press, 2009. [24] 张丽丽, 赵泽茂, 包建荣. 基于Z形及等差数列结构的QC-LDPC码构造[J]. 通信学报, 2010, 31(8A): 117–121.ZHANG Lili, ZHAO Zemao, and BAO Jianrong. Construct of QC-LDPC codes based on Z-shape and arithmetic progression sequence[J]. Journal on Communications, 2010, 31(8A): 117–121. -





 下载:
下载:

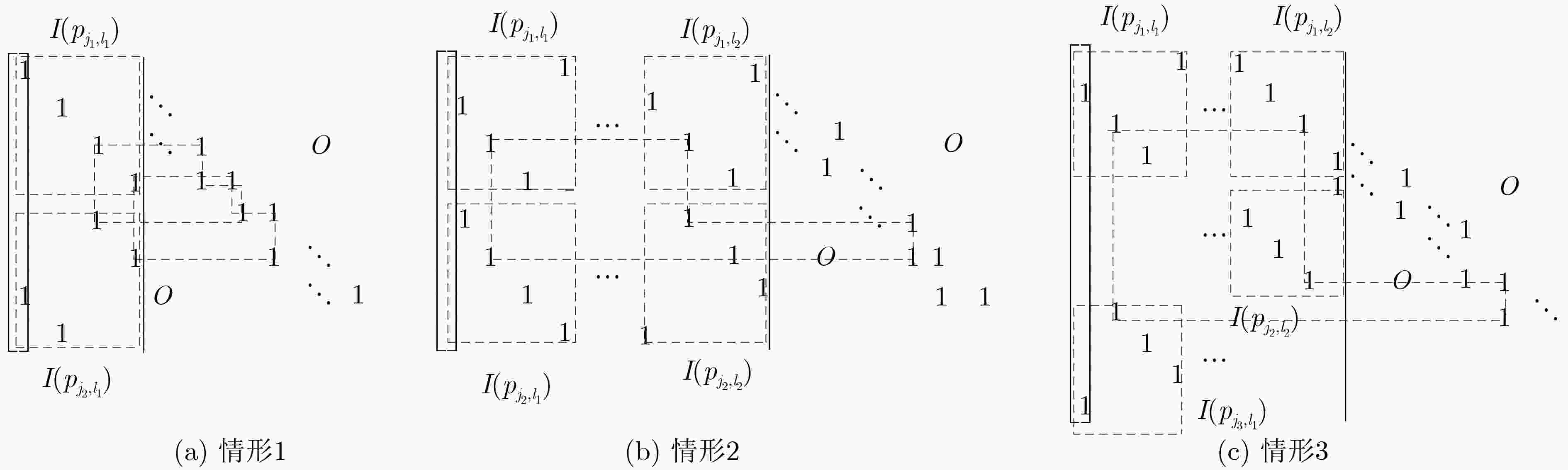


 下载:
下载:
