探地雷达频率域2.5维正演

戴世坤; 欧阳振崇; 周印明; 张钱江; 李昆; 赵东东; 陈轻蕊; 凌嘉宣

doi:10.11999/JEIT190988

探地雷达频率域2.5维正演

doi: 10.11999/JEIT190988

戴世坤^{1, 2},
欧阳振崇^{1, 2, ,},
周印明³,
张钱江⁴,
李昆^{1, 2},
赵东东^{1, 2},
陈轻蕊^{1, 2},
凌嘉宣^{1, 2}

1.
中南大学地球科学与信息物理学院长沙 410083
2.
中南大学有色金属成矿预测与地质环境监测教育部重点实验室长沙 410083
3.
东方地球物理公司综合物化探处涿州 072751
4.
桂林理工大学地球科学学院桂林 541006

基金项目: 国家重点研发计划(2018YFC0603602)，国家自然科学基金(41574127)，中南大学研究生自主探索创新项目(2018zzts707, 2018zzts200, 2018zzts203)

详细信息

作者简介:
戴世坤：男，1964年生，教授，主要研究方向为重、磁、电、地震2维3维高效、高精度数值模拟与反演成像理论、方法和技术研究等

欧阳振崇：男，1995年生，硕士生，研究方向为频率域雷达2.5维3维高效、高精度数值模拟与反演成像研究

通讯作者:
欧阳振崇　oyzc_wy@163.com

中图分类号: TN959
计量
- 文章访问数: 2152
- HTML全文浏览量: 769
- PDF下载量: 105
- 被引次数: 7
出版历程
- 收稿日期: 2019-12-11
- 修回日期: 2020-08-08
- 网络出版日期: 2020-08-21
- 刊出日期: 2021-01-15

Frequency Domain 2.5D GPR Forward Modeling

Shikun DAI^{1, 2},
Zhenchong OUYANG^{1, 2
, ,},
Yinming ZHOU³,
Qianjiang ZHANG⁴,
Kun LI^{1, 2},
Dongdong ZHAO^{1, 2},
Qingrui CHEN^{1, 2},
Jiaxuan LING^{1, 2}

1.
School of Geosciences and Info-physics, Central South University, Changsha 410083, China
2.
Key Laboratory of Metallogenic Prediction of Nonferrous Metals and Geological Environment Monitoring of Ministry of Education, Central South University, Changsha 410083, China
3.
Department of Non-seismic Exploration, Bureau of Geophysical Prospecting, Zhuozhou 072751, China
4.
School of Earth Science of Guilin University of Technology, Guilin 541006, China

Funds: The National Key Research and Development Project (2018YFC0603602), The National Natural Science Foundation of China (41574127), The Project for the Independent Exploration of Graduate Students at Central South University (2018zzts707, 2018zzts200, 2018zzts203)

摘要

摘要:
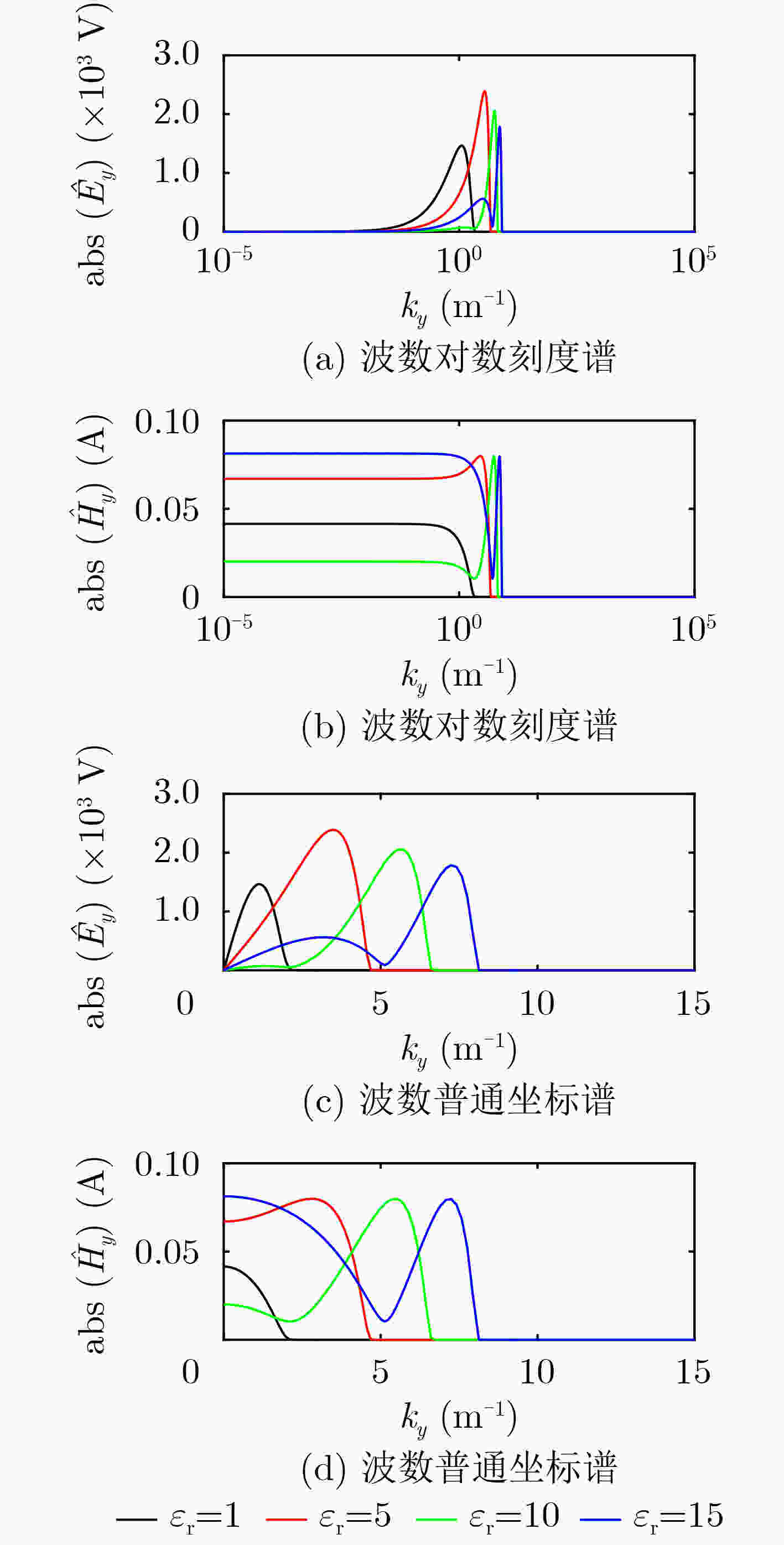
该文从频率域电磁法满足的控制方程出发，采用有限单元法实现了频率域2.5维探地雷达(GPR)正演模拟。重点分析了波数域电磁场谱随相对介电常数和收发距变化的规律，探讨了2.5维GPR正演模拟的波数选取问题；基于Open MP并行算法与串行算法的计算效率对比，表明频率域2.5维GPR数值模拟方法具有高效率、高精度和高度并行性的特点，为雷达正演提供重要理论参考依据和技术支撑，是GPR全波形反演的重要基础。
- 探地雷达 /
- 正演 /
- 2.5维 /
- 频率域 /
- 波数选取 /
- Open MP /
- 并行
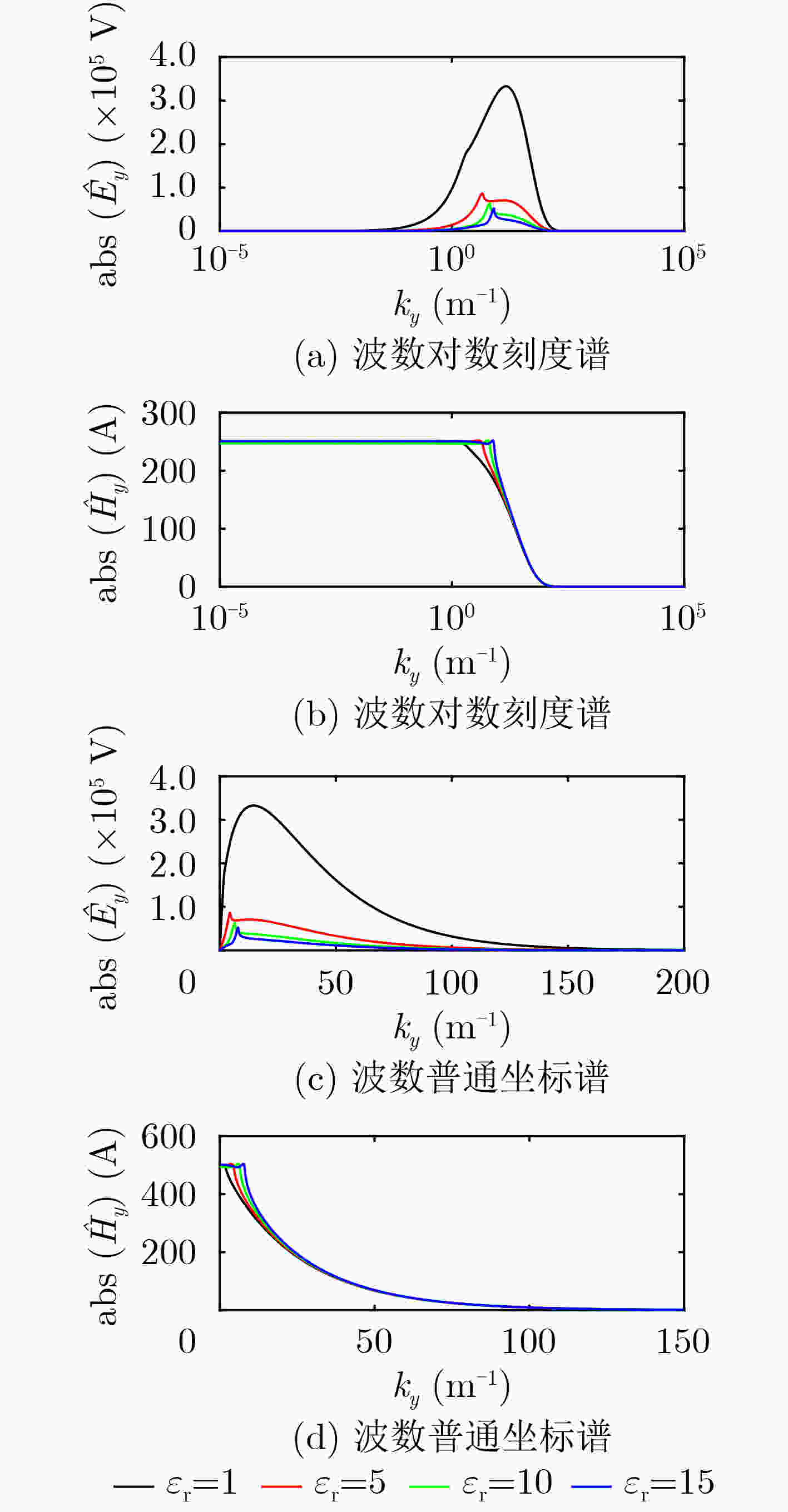
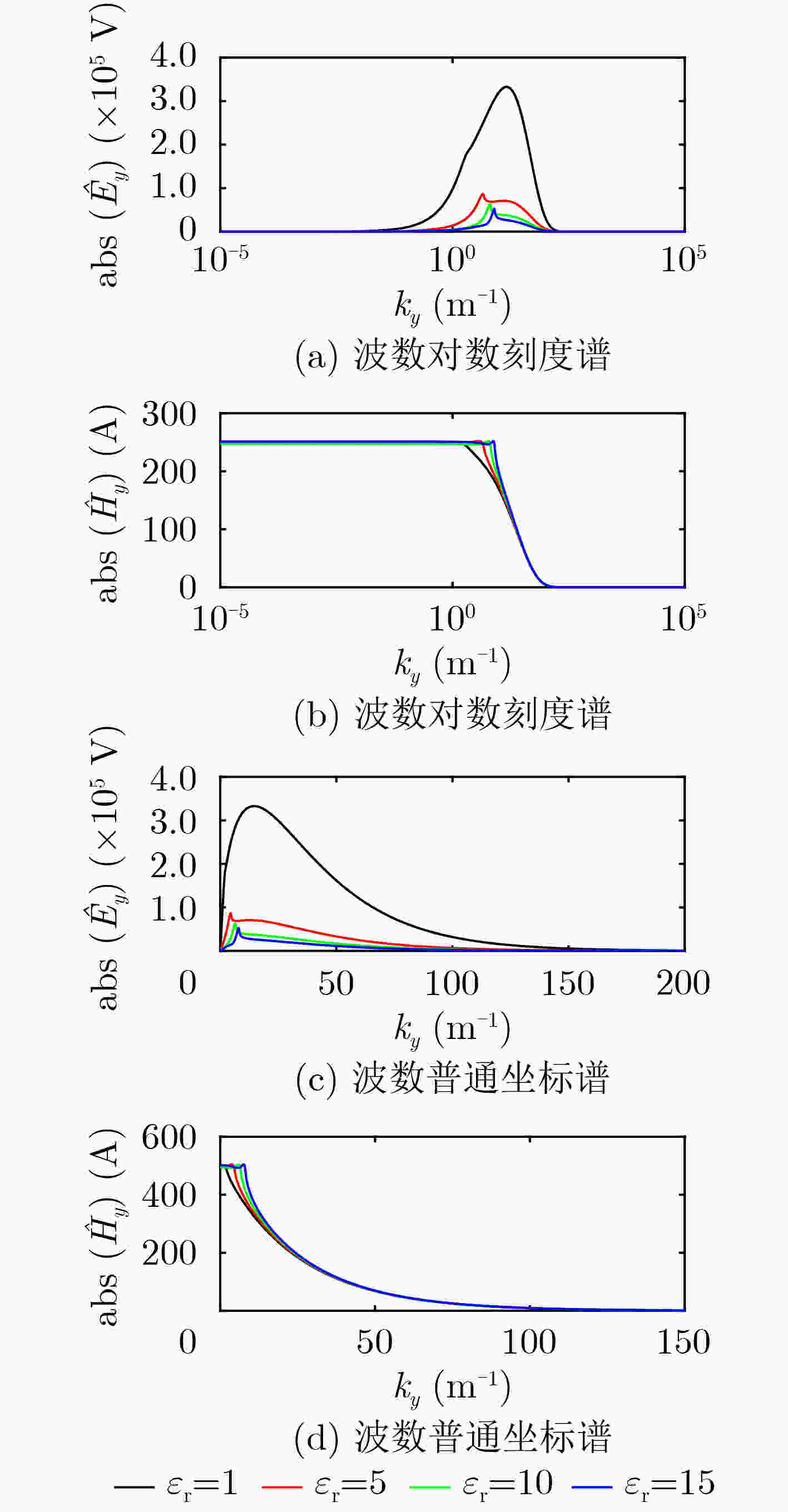
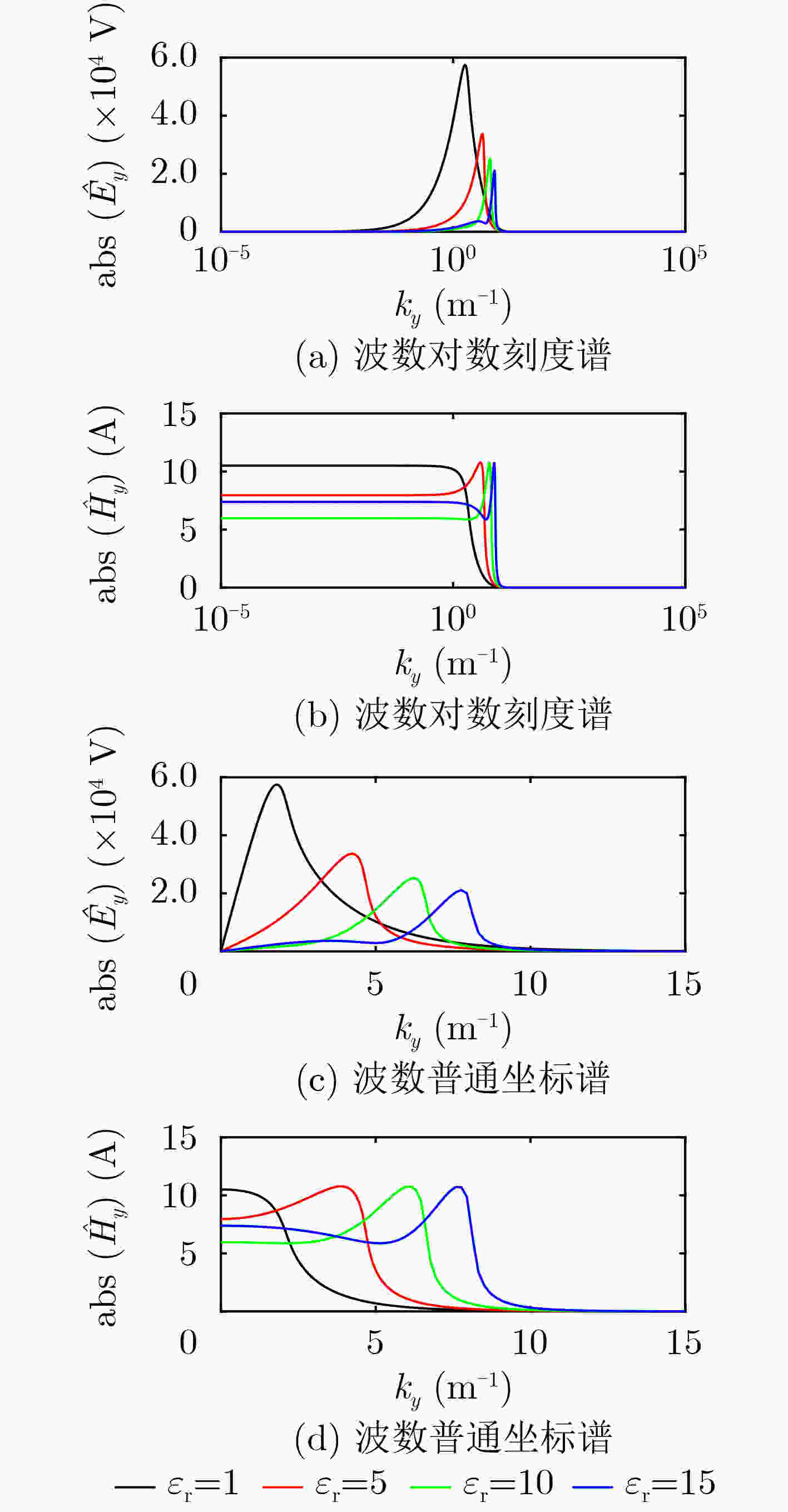
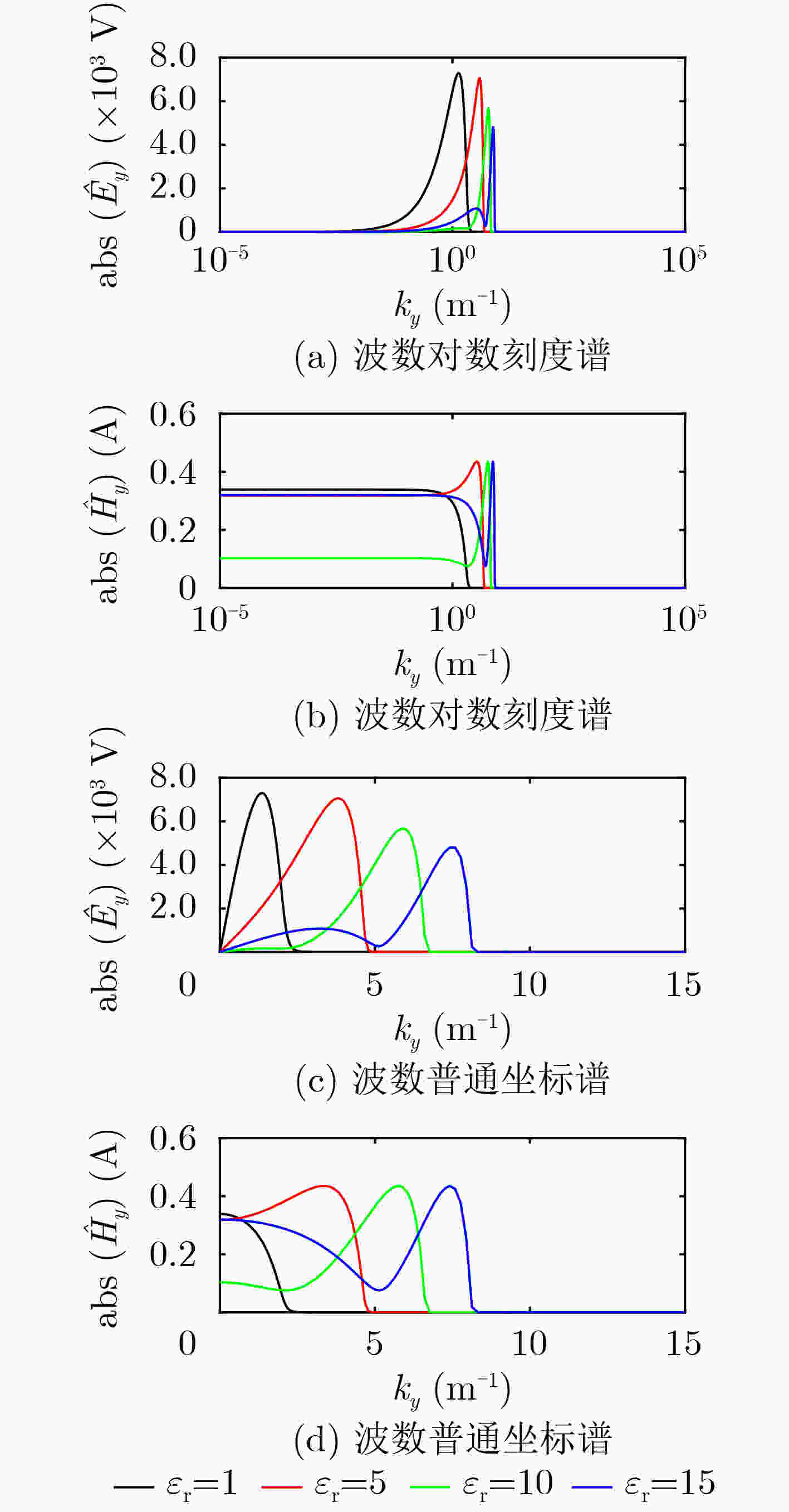
Abstract:
Based on the governing equations satisfied by the electromagnetic method of the frequency domain, the finite element method is used to realize the forward simulation of 2.5-Dimensional a (2.5D) Ground Penetrating Radar (GPR) in the frequency domain. The law of the electromagnetic field spectrum in the wavenumber domain with the relative permittivity and the transmission and reception distance is analyzed in detail. The selection of the wave number in the 2.5D GPR forward modeling simulation is discussed. Based on the comparison of the computational efficiency of the Open MP parallel algorithm and the serial algorithm, the results show that the 2.5D GPR numerical simulation method in the frequency domain has the characteristics of high efficiency, high precision, and high parallelism. It provides important theoretical reference and technical support for radar forward modeling, and provides an important foundation for GPR full waveform inversion.
- Ground Penetrating Radar (GPR) /
- Forward modeling /
- 2.5-Dimensional (2.5D) /
- Frequency domain /
- Wave number selection /
- Open MP /
- Parallel

HTML全文

1. 引言

探地雷达(Ground Penetrating Radar, GPR)是一种利用高频(10⁶～10⁹ Hz)电磁波来确定介质内部物质分布规律的地球物理方法，因其具有抗干扰能力强、探测分辨率高、场地适应能力强、操作简单且为无损探测等优势而被广泛地应用于工程勘察及地质调查。GPR正演是雷达理论研究的重点之一，随着勘探要求更加精细化和高效，大范围高效、高精度的数值模拟和反演成像成为现在GPR技术的目标^[1,2]。

波动方程正演模拟方法，因其能包含雷达波的运动学特征和动力学特征被广泛应用于GPR正演模拟中，主要包括时域有限差分法(Finite-Difference Time Domain method, FDTD)和有限单元法(Finite Element Method, FEM)两种。在FDTD法的应用方面，自1996年Yee^[3]提出著名的Yee氏网格后，FDTD法被广泛应用于GPR数值模拟中。Bergmann等人^[4]应用FDTD法开展了不均匀非线性和衰减介质的GPR正演模拟；Irving等人^[5]采用PML吸收边界研究了TE和TM模式的2维GPR数值模拟；刘四新等人^[6]对比了GPR2维频散介质与非频散介质中GPR信号的区别；冯德山等人^[7]研究了FDTD数值模拟中不分裂卷积完全匹配层对倏逝波的吸收效果。

FDTD法原理简单，易于编程实现，但要求模型规则剖分，对复杂问题适应性差。FEM因具有网格剖分灵活，适用于物性参数分布复杂和几何特征不规则模型的优势，被引入到GPR数值模拟领域。底青云等人^[8]推导GPR有限元方程，开展了一系列典型模型的正演模拟；杜华坤等人^[9]基于优化的Delaunay三角剖分，采用线性插值进行了FEM的GPR2维正演，提高了FEM对复杂模型模拟的适应性和数值模拟精度；石明等人^[10]采用Delaunay非结构化网格有限元法进行了各向异性介质GPR有限元正演；王洪华等人^[11]实现了PML边界条件在2阶电磁波动方程GPR时域有限元模拟中的应用，验证了PML边界条件在复杂地电结构电磁波传播模拟中具有良好的吸收效果。

近年来GPR数值模拟大都在时间域内研究，时间域GPR波的传播满足的波动方程模拟结果符合雷达波传播的运动学特征，但在表现波的动力学特征方面存在不足，文献[12]指出频率域波形反演在地震中的重要地位，首次研究了频率域波形反演，对频域波形反演存在的问题进行了初次探讨，本文从频率域出发，研究了2.5维GPR数值模拟方法，这样可以很好地保留雷达波传播的运动学特征和动力学特征，准确地研究雷达波在频率域的传播特性，为GPR全波形反演提供重要基础。本文采用有限单元法，推导基于行波分解的吸收边界条件的GPR有限元方程，实现频率域2.5D探地雷达正演模拟。重点分析和总结在雷达频率不同相对介电常数和不同收发距波数选取的规律；设计均匀全空间和半空间模型，将数值解与解析解对比验证了算法的正确性；另外，雷达2.5维频率域正演在不同波数之间的计算具有高度并行性，通过设计Open MP并行，探究不同线程下算法并行的效率，验证了算法的高效性。

2. 方法理论

2.1 控制方程

设时谐因子 ${{\rm{e}}^{{\rm{i}}\omega t}}$ , $w = 2{\rm{\pi}} f$ 为角频率，f为频率，有源区域的频率域Maxwell方程有表达式

$\qquad\quad\nabla \times E = - \hat zH - z{M_{\rm{s}}}$

(1)

$\qquad\quad \nabla \times H = \hat yE + {J_{\rm{s}}}$

(2)

其中，E为电场强度，H为磁场强度， ${M_{\rm{s}}}$ 为源磁极化强度； ${J_{\rm{s}}}$ 为源电流密度， $\hat z = {\rm{i}}w\mu$ 表示阻抗率， $\hat y = {\rm{i}}\varepsilon w + \sigma$ 表示导纳率，式中 $\varepsilon = {\varepsilon _{\rm{r}}}{\varepsilon _0}$ 为介电常数， ${\varepsilon _{\rm{r}}}$ 为相对介电常数， $\sigma$ 为电导率， $\mu$ 为磁导率。

设x轴水平向右为正，z轴垂直向上为正，y轴为构造走向，沿y方向作1维傅里叶变换，变换式为

$\hat F\left( {x,{k_y},z,{\rm{\omega}} } \right) = \int\limits_{ - \infty }^\infty {F\left( {x,y,z,{\rm{\omega}} } \right)} {{\rm{e}}^{ - {\rm{i}}{k_y}y}}{\rm{d}}y$

(3)

其中，(x, y, z)为空间坐标， ${k_y}$ 为波数， $\hat F$ 为波数域电磁场值， $F$ 为空间域电磁场值，将Maxwell方程组式(1)和式(2)展开可求得控制方程^[13]

$\begin{split} & \frac{\partial }{{\partial x}}\left( {\frac{{\hat y}}{{k_e^2}}\frac{{\partial {{\hat E}_y}}}{{\partial x}}} \right) + \frac{\partial }{{\partial z}}\left( {\frac{{\hat y}}{{k_e^2}}\frac{{\partial {{\hat E}_y}}}{{\partial z}}} \right) - \hat y{{\hat E}_y} \\ & \qquad + {\rm{i}}{k_y}\left[ {\frac{\partial }{{\partial x}}\left( {\frac{1}{{k_e^2}}} \right)\frac{{\partial {{\hat H}_y}}}{{\partial z}} - \frac{\partial }{{\partial z}}\left( {\frac{1}{{k_e^2}}} \right)\frac{{\partial {{\hat H}_y}}}{{\partial x}}} \right] \\ & \quad= {{\hat J}_{{\rm{sy}}}} - {\rm{i}}{k_y}\left[ {\frac{\partial }{{\partial x}}\left( {\frac{1}{{k_e^2}}{{\hat J}_{{\rm{s}}x}}} \right) + \frac{\partial }{{\partial z}}\left( {\frac{1}{{k_e^2}}{{\hat J}_{{\rm{s}}z}}} \right)} \right] \\ & \qquad + \frac{\partial }{{\partial x}}\left( {\frac{{{k^2}}}{{k_e^2}}{{\hat M}_{{\rm{s}}z}}} \right) - \frac{\partial }{{\partial z}}\left( {\frac{{{k^2}}}{{k_e^2}}{{\hat M}_{{\rm{s}}x}}} \right) \end{split}$

(4)

$\begin{split} & \frac{\partial }{{\partial x}}\left( {\frac{{\hat z}}{{k_e^2}}\frac{{\partial {{\hat H}_y}}}{{\partial x}}} \right) + \frac{\partial }{{\partial z}}\left( {\frac{{\hat z}}{{k_e^2}}\frac{{\partial {{\hat H}_y}}}{{\partial z}}} \right) - \hat z{{\hat H}_y} \\ & \qquad + {\rm{i}}{k_y}\left[ { - \frac{\partial }{{\partial x}}\left( {\frac{1}{{k_e^2}}} \right)\frac{{\partial {{\hat E}_y}}}{{\partial z}} + \frac{\partial }{{\partial z}}\left( {\frac{1}{{k_e^2}}} \right)\frac{{\partial {{\hat E}_y}}}{{\partial x}}} \right] \\ & \quad=\hat z{{\hat M}_{{\rm{sy}}}} - {\rm{i}}{k_y}\left[ {\frac{\partial }{{\partial x}}\left( {\frac{{\hat z}}{{k_e^2}}{{\hat M}_{{\rm{s}}x}}} \right) + \frac{\partial }{{\partial z}}\left( {\frac{{\hat z}}{{k_e^2}}{{\hat M}_{{\rm{s}}z}}} \right)} \right] \\ & \qquad + \frac{\partial }{{\partial x}}\left( {\frac{{\hat z}}{{k_e^2}}{{\hat J}_{{\rm{s}}z}}} \right) - \frac{\partial }{{\partial z}}\left( {\frac{{\hat z}}{{k_e^2}}{{\hat J}_{{\rm{s}}x}}} \right)\\[-17pt] \end{split}$

(5)

式中， ${k^2} = - \hat z\hat y$ , $k_e^2 = k_y^2 - {k^2}$ ，式(4)和式(5)为波数域 ${\hat E_y}$ 和 ${\hat H_y}$ 的耦合控制方程组，这两个控制方程考虑了电导率和介电常数的影响，既可在高频段进行GPR数值模拟，又可在低频段进行CSEM数值模拟。

辅助场的表达式为^[13]

$\begin{split} & {\hat E_x} = \frac{1}{{k_e^2}}\left( { - {\rm{i}}{k_y}\frac{{\partial {{\hat E}_y}}}{{\partial x}} - \hat z\frac{{\partial {{\hat H}_y}}}{{\partial z}} - \hat z{{\hat J}_{{\rm{s}}x}} - {\rm{i}}{k_y}\hat z{{\hat M}_{{\rm{s}}z}}} \right),\\ & {\hat E_z} = \frac{1}{{k_e^2}}\left( { - {\rm{i}}{k_y}\frac{{\partial {{\hat E}_y}}}{{\partial z}} + \hat z\frac{{\partial {{\hat H}_y}}}{{\partial x}} - \hat z{{\hat J}_{{\rm{s}}z}} + {\rm{i}}{k_y}\hat z{{\hat M}_{{\rm{s}}x}}} \right) \end{split}$

(6)

$\begin{split} & {\hat H_x} = \frac{1}{{k_e^2}}\left( { - {\rm{i}}{k_y}\frac{{\partial {{\hat H}_y}}}{{\partial x}} + \hat y\frac{{\partial {{\hat E}_y}}}{{\partial z}} + {k^2}{{\hat M}_{{\rm{s}}x}} + {\rm{i}}{k_y}{{\hat J}_{{\rm{s}}z}}} \right),\\ & {\hat H_z} = \frac{1}{{k_e^2}}\left( { - {\rm{i}}{k_y}\frac{{\partial {{\hat H}_y}}}{{\partial z}} - \hat y\frac{{\partial {{\hat E}_y}}}{{\partial x}} + {k^2}{{\hat M}_{{\rm{s}}z}} - {\rm{i}}{k_y}{{\hat J}_{{\rm{s}}x}}} \right) \end{split}$

(7)

2.2 有限单元法

利用Galerkin法导出有限元方程

$\begin{split} & \sum\limits_{e = 1}^{Ne} \iint\limits_{De} \left\{ \frac{{\partial N_i^e}}{{\partial x}}\left( {\frac{{\hat y}}{{k_e^2}}\frac{{\partial {{\hat E}_y}}}{{\partial x}}} \right) \!+\! \frac{{\partial N_i^e}}{{\partial z}}\left( {\frac{{\hat y}}{{k_e^2}}\frac{{\partial {{\hat E}_y}}}{{\partial z}}} \right) \!+\! N_i^e\hat y{{\hat E}_y} \right.\\ & \qquad \left.+ \frac{{{\rm{i}}{k_y}}}{{k_e^2}}\left( {\frac{{\partial N_i^e}}{{\partial x}}\frac{{\partial {{\hat H}_y}}}{{\partial z}} - \frac{{\partial N_i^e}}{{\partial z}}\frac{{\partial {{\hat H}_y}}}{{\partial x}}} \right) \right\}{\rm{d}}x{\rm{d}}z \\ & \quad = - \sum\limits_{e = 1}^{Ne}\iint\limits_{De} \left\{ N_i^e{{\hat J}_{sy}} + \frac{{{\rm{i}}{k_y}}}{{k_e^2}}\left( {\frac{{\partial N_i^e}}{{\partial x}}{{\hat J}_{{\rm{s}}x}} + \frac{{\partial N_i^e}}{{\partial z}}{{\hat J}_{{\rm{s}}z}}} \right) \right.\\ & \qquad \left.+ \frac{{{k^2}}}{{k_e^2}}\left( {\frac{{\partial N_i^e}}{{\partial z}}{{\hat M}_{{\rm{s}}x}} - \frac{{\partial N_i^e}}{{\partial x}}{{\hat M}_{{\rm{s}}z}}} \right) \right\}{\rm{d}}x{\rm{d}}z\\ & \qquad {\rm{ + }}\sum\limits_{e = 1}^{Ne} {\oint\limits_{De} {N_i^e( - {{\hat H}_z}{n_x} + } } {{\hat H}_x}{n_z}) {\rm{d}}l \\[-21pt] \end{split}$

(8)

$\begin{split} & \sum\limits_{e = 1}^{Ne} \iint\limits_{De} \left\{ \frac{{\partial N_i^e}}{{\partial x}}\left( {\frac{{\hat z}}{{k_e^2}}\frac{{\partial {{\hat H}_y}}}{{\partial x}}} \right) \!+\! \frac{{\partial N_i^e}}{{\partial z}}\left( {\frac{{\hat z}}{{k_e^2}}\frac{{\partial {{\hat H}_y}}}{{\partial z}}} \right) \!+\! N_i^e\hat z{{\hat H}_y} \right.\\ & \qquad \left.+ \frac{{{\rm{i}}{k_y}}}{{k_e^2}}\left( { - \frac{{\partial N_i^e}}{{\partial x}}\frac{{\partial {{\hat E}_y}}}{{\partial z}} + \frac{{\partial N_i^e}}{{\partial z}}\frac{{\partial {{\hat E}_y}}}{{\partial x}}} \right) \right\}{\rm{d}}x{\rm{d}}z \\ & \quad = \!-\! \sum\limits_{e = 1}^{Ne} \iint\limits_{De} \left\{ N_i^e{{\hat M}_{{\rm{s}}y}} \!+\! \frac{{{\rm{i}}{k_y}\hat z}}{{k_e^2}}\left( {\frac{{\partial N_i^e}}{{\partial x}}{{\hat M}_{{\rm{s}}x}} \!+\! \frac{{\partial N_i^e}}{{\partial z}}{{\hat M}_{{\rm{s}}z}}} \right)\right. \\ & \qquad \left.+ \frac{{\hat z}}{{k_e^2}}\left( {\frac{{\partial N_i^e}}{{\partial z}}{{\hat J}_{{\rm{s}}x}} - \frac{{\partial N_i^e}}{{\partial x}}{{\hat J}_{{\rm{s}}z}}} \right) \right\}{\rm{d}}x{\rm{d}}z \\ &\qquad - \sum\limits_{e = 1}^{Ne} {\oint\limits_{De} {N_i^e( - {{\hat E}_z}{n_x} + } } {{\hat E}_x}{n_z}){\rm{d}}l \\[-21pt] \end{split}$

(9)

首先采用四边形单元剖分，然后利用交叉对称网格的三角形单元第2次离散，三角形单元中采用线性插值。对式(8)和式(9)通过单元分析和总体合成得到一个大型、稀疏的复线性方程组，求解该方程组得到波数域 ${\hat E_y}$ 和 ${\hat H_y}$ ，再根据式(6)和式(7)求得波数域其他电磁场分量( ${\hat E_x}$ , ${\hat E_z}$ , ${\hat H_x}$ 和 ${\hat H_z}$ )，其中 $\partial {\hat E_y}/\partial x,\partial {\hat E_y}/\partial z,\partial {\hat H_y}/\partial y,\partial {\hat H_y}/\partial z$ 采用差分法计算。最后将波数域电磁场采用傅里叶逆变换即可得到空间域电磁场。本文采用文献[13]中的方法对源进行处理，引入文献[14]中基于行波分解法的吸收边界对边界进行处理，提高计算精度。

3. 数值算例

本文算法的程序代码采用Fortran语言编写，测试平台配置为CPU-Inter(R) Core(TM) i9-7980XE，主频2.60 GHz(18核，36线程)，内存64 GB, 64位操作系统。

3.1 波场参数分析

波数选取是电磁法2.5D数值模拟中一个很重要的环节。根据经验，波数谱的能量分布与频率大小无关，仅与收发距有关。本文波数除0波数外，其他波数采用对数域等间隔采样，负波数与正波数互为相反数。设正波数最小值和最大值分别为k_ymin, k_ymax，设区间个数N=lgk_ymax–lgk_ymin, N取整数，在每个数量级等间隔采样。经测试，在2.5DGPR正演时k_ymin取10^–4合适，k_ymax与最小网格间距r_min有关，经验公式 ${k_{y\max}} = 10/{r_{\min}}$ 。

研究同一频率下 ${\varepsilon _r}$ 和收发距r对波数选取的影响。设计全空间模型，电阻率1000 $\Omega/{\rm{m}}$ ，电流1000 A，频率100 MHz，源中心在原点，偶极距1 m，AB电极(–0.5, 0)和(0.5, 0)。利用均匀全空间 ${\hat E_y}$ 和 ${\hat H_y}$ 解析解，计算 ${\varepsilon _{\rm{r}}}$ 分别为1.0, 5.0, 10.0和15.0的谱，测点垂直z方向坐标为0.02 m, x方向坐标为0.1 m, 0.5 m, 1 m, 5 m和10 m，计算结果如图1—图5。

图 1 d_x=0.1 m处不同相对介电常数的电磁场谱随波数变化特征

下载: 全尺寸图片幻灯片

图 2 d_x=0.5 m处不同相对介电常数电磁场谱随波数变化特征

下载: 全尺寸图片幻灯片

图 3 d_x=1 m处不同相对介电常数电磁场谱随波数变化特征

下载: 全尺寸图片幻灯片

图 4 d_x=5 m处不同相对介电常数电磁场谱随波数变化特征

下载: 全尺寸图片幻灯片

图 5 d_x=10 m处不同相对介电常数电磁场谱随波数变化特征

下载: 全尺寸图片幻灯片

由图1—图5对比可看出， ${\hat E_y}$ 谱的振幅在水平0.5 m处即电极处最大，主要能量集中在 ${k_y} \le 200$ 范围， ${\hat E_y}$ 振幅和主要能量集中范围随距离电极增大而减小；当测点距离源电极大于1 m时， ${\hat E_y}$ 谱的振幅数值迅速减小，能量范围集中在波数 ${k_y} \le 10$ 范围； ${\hat H_y}$ 谱在距离源中心水平0.1 m时， ${\hat H_y}$ 谱的振幅最大，主要能量集中范围 ${k_y} \le 150$ ，振幅和主要能量集中范围随距离源中心点增大而减小，电极附近，磁场谱的能量迅速减小，当测点距离源中心大于1 m时，能量范围集中在波数 ${k_y} \le 10$ 的范围内，谱能量分布规律与相对介电常数大小无关；同一测点的谱能量振幅最大值所对应的波数均随着 ${\varepsilon _r}$ 增大而增大，在距离源近区r≤1 m, ${\hat E_y}$ 谱的能量幅值随着 ${\varepsilon _r}$ 的增大而减小，远区无明显规律， ${\hat H_y}$ 谱的能量幅值随着 ${\varepsilon _r}$ 增大而增大，远区无明显规律。

结论：频率为100 MHz，计算距离范围为10 m时，波数最大值选取10³即可将谱的能量全包含其中，而且谱的能量主要分布在波数0～10的范围内，可对该范围内波数适当加密，使傅里叶逆变换精度更高。

3.2 正确性验证

3.2.1 全空间模型

设计均匀全空间模型， $\sigma = {\rm{0}}{\rm{.001}}\;{\rm{S/m}}$ , ${\varepsilon _{\rm{r}}} = 1.0$ ，节点301×301，电流1000 A，偶极距dl为1 m，源中心在原点，x方向源网格均0.02 m，源以外网格采用非均匀剖分最大0.05 m，边界取15个网格间距由0.05 m以1.5倍递增至1 m。x, z方向网格剖分相同，f=100 MHz，正波数范围(0.01, 1000)，波数55个。

图6中主剖面上电磁场数值解与解析解的形态、数值都相同，主剖面测线z=0.5 m处各节点的相对误差均小于1%，验证了本文算法的正确性。

图 6 主剖面电磁场数值解与解析解对比图

下载: 全尺寸图片幻灯片

图7为采用文献[15]中的算法计算主剖面电磁场的数值解与解析解对比图，由图可知，文献[15]算法在源附近的误差较大，表明本文算法在源的处理上要优于文献[15]中的算法，计算精度更高。

图 7 主剖面电磁场其他算法数值解与解析解对比图

下载: 全尺寸图片幻灯片

3.2.2 半空间模型

设计均匀半空间模型，空气层电导率 $\sigma = {10^{ - 12}}\;{\rm{S/m}}$ ，地下介质电导率 $\sigma = {10^{ - 3}}\,\;{\rm{S/m}}$ ，相对介电常数 ${\varepsilon _{\rm{r}}} = 1.0$ ，频率f=100 MHz，网格节点601×601，x方向的源布设于地下0.5 m，源的其他参数和网格剖分与全空间相同，选取正波数范围(0.0001, 1000)，波数277个。

图8为主剖面(y = 0 m)数值解与解析解对比，第3列为剖面测线z=0.5 m的相对误差，由图可知，数值解与解析解的形态、数量级相同，测线各节点的相对误差均小于1.5%，同样验证了本文算法的准确性。

图 8 主剖面半空间电磁场数值解与解析解的对比图

下载: 全尺寸图片幻灯片

3.3 Open MP并行测试

本文算法耗时主要在波数循环计算上，每个波数均需求解1次方程组，但各波数计算相互独立，可采用并行方式提高计算效率。目前电磁法2.5D正反演应用较多的并行方法有MPI(Message Passing Interface)和OpenMP(Open Multi-Processing)。OpenMP使用线程间共享内存的方式协调并行计算，对原串行代码改动小，容易实现。本文采用OpenMP并行处理不同波数方程组的求解、傅里叶逆变换和辅助场计算。

2.5D GPR正演计算量大，将Pardiso求解器采用OpenMP并行求解，算法效率如表1。模型参数与3.2.1小节模型一致，网格节点301×301，波数277个。式中加速比 = 单机的单线程耗时/并行计算耗时。

表 1 整个程序OpenMP并行不同线程计算效率

	1线程	2线程	4线程	8线程	16线程	20线程
CPU负载率(%)	78.7	9.2	19.2	37.7	72.6	90.3
占用内存(GB)	1.32	1.95	2.86	5.84	10.16	13.26
运行时间(s)	242.887	359.917	190.912	106.645	79.925	86.375
加速比(SP)	无	0.673	1.269	2.271	3.030	2.812

下载: 导出CSV

| 显示表格

表1中，随着并行线程个数增加，加速比增大，算法耗时减少，改造后的计算效率明显提高。2线程耗时比单线程耗时长，可能原因是2线程时发生了同步事件，耗时变长^[16]；16线程耗时约80 s，比单线程计算快了3倍；增加到20线程时，耗时反倒增大，分析原因是当计算量一定时，线程数量增加，用于线程通信/线程调度的时间所占比例逐渐增大，计算效率降低。

结论：采用OpenMP将Pardiso求解器并行，随着并行线程个数增加，计算效率提高，但并行线程数并非越多越好，综合不同线程算法耗时和计算机资源的占用情况，本节线程数为16时，加速比最大，耗时最短，是当前条件下OpenMP并行选取的最佳线程数。

3.4 复杂模型算例

设计均匀半空间中存在两个异常体，异常体的模型参数如图9所示，源和网格等模型参数均与3.2.2小节中半空间模型相同。

图 9 复杂模型示意图

下载: 全尺寸图片幻灯片

图10为主剖面电磁场响应特征，图中可看出异常体的位置和形状，低阻异常体相对介电常数大，电磁波长小，电磁场波动明显；高阻体相对介电常数略小，异常反应不如低阻体灵敏，电磁场波动小，说明波场对介质不均匀性有一定程度的敏感度，说明本文提出的GPR正演算法对于复杂模型具有很好的适应性。

图 10 主剖面电磁场分量实部和虚部

下载: 全尺寸图片幻灯片

4. 结论

本文采用有限单元法，推导了基于行波分解的吸收边界条件的GPR有限元方程，保留雷达波传播的运动学特征和动力学特征，实现了频率域2.5D探地雷达正演模拟。主要有以下结论：

(1) GPR2.5D正演波数选取规律： ${\hat E_y}$ 谱电极处能量最大，振幅和主要能量集中范围随着离电极的距离的增大而减小； ${\hat H_y}$ 谱场源中心能量最大，振幅和主要能量集中范围随离场源中心距离增大而减小；测点谱的能量最大的波数值随着 ${\varepsilon _{\rm{r}}}$ 的增大而增大；频率100 MHz，均匀全空间计算范围10 m，波数最大值选取10³即可，波数区间0～10需要加密选取波数，这个规律与 ${\varepsilon _{\rm{r}}}$ 的大小无关。

(2) 均匀全空间和半空间模型数值解与解析解除源处之外的剖面节点误差均小于1%，表明算法正确。

(3) 测试平台CPU-Inter(R) Core(TM) i9-7980XE，主频2.60 GHz(36核)，内存64 GB，64位操作系统，节点301×301、波数277时，并行最优线程数是16，此时算法耗时80 s，比一个线程计算时的速度快了3倍，验证了算法的高度并行性和高效性。

(4) 传统探地雷达的发射源在空气中，本文采用接地线源，这样做更方便能量的辐射，研究雷达波在频率域的传播特性，完善雷达的电磁理论，为GPR全波形反演提供重要基础。

图 1 d_x=0.1 m处不同相对介电常数的电磁场谱随波数变化特征

下载: 全尺寸图片幻灯片

图 2 d_x=0.5 m处不同相对介电常数电磁场谱随波数变化特征

下载: 全尺寸图片幻灯片

图 3 d_x=1 m处不同相对介电常数电磁场谱随波数变化特征

下载: 全尺寸图片幻灯片

图 4 d_x=5 m处不同相对介电常数电磁场谱随波数变化特征

下载: 全尺寸图片幻灯片

图 5 d_x=10 m处不同相对介电常数电磁场谱随波数变化特征

下载: 全尺寸图片幻灯片

图 6 主剖面电磁场数值解与解析解对比图

下载: 全尺寸图片幻灯片

图 7 主剖面电磁场其他算法数值解与解析解对比图

下载: 全尺寸图片幻灯片

图 8 主剖面半空间电磁场数值解与解析解的对比图

下载: 全尺寸图片幻灯片

图 9 复杂模型示意图

下载: 全尺寸图片幻灯片

图 10 主剖面电磁场分量实部和虚部

下载: 全尺寸图片幻灯片

表 1 整个程序OpenMP并行不同线程计算效率

	1线程	2线程	4线程	8线程	16线程	20线程
CPU负载率(%)	78.7	9.2	19.2	37.7	72.6	90.3
占用内存(GB)	1.32	1.95	2.86	5.84	10.16	13.26
运行时间(s)	242.887	359.917	190.912	106.645	79.925	86.375
加速比(SP)	无	0.673	1.269	2.271	3.030	2.812

下载: 导出CSV

参考文献(16)

屈乐乐, 方广有, 杨天虹. 压缩感知理论在频率步进探地雷达偏移成像中的应用[J]. 电子与信息学报, 2011, 33(1): 21–26. doi: 10.3724/SP.J.1146.2009.01528

QU Lele, FANG Guangyou, and YANG Tianhong. The application of compressed sensing to stepped-frequency ground penetrating radar migration imaging[J]. Journal of Electronics &Information Technology, 2011, 33(1): 21–26. doi: 10.3724/SP.J.1146.2009.01528

郑适, 张安学, 岳思橙, 等. 基于改进粒子群优化的探地雷达波形反演算法[J]. 电子与信息学报, 2014, 36(11): 2717–2722. doi: 10.3724/SP.J.1146.2013.01979

ZHENG Shi, ZHANG Anxue, YUE Sicheng, et al. Ground penetrating radar inversion algorithm based on improved particle swarm optimization[J]. Journal of Electronics &Information Technology, 2014, 36(11): 2717–2722. doi: 10.3724/SP.J.1146.2013.01979

YEE K. Numerical solution of initial boundary value problems involving Maxwell’s Equations in isotropic media[J]. IEEE Transactions on Antennas and Propagation, 1996, 14(3): 302–307.

BERGMANN T, ROBERTSSON J O A, and HOLLIGER K. Finite-difference modeling of electromagnetic wave propagation in dispersive and attenuating media[J]. Geophysics, 1998, 63(3): 856–867. doi: 10.1190/1.1444396

IRVING J and KNIGHT R. Numerical modeling of ground-penetrating radar in 2-D using MATLAB[J]. Computers & Geosciences, 2006, 32(9): 1247–1258. doi: 10.1016/j.cageo.2005.11.006

刘四新, 曾昭发. 频散介质中地质雷达波传播的数值模拟[J]. 地球物理学报, 2007, 50(1): 320–326. doi: 10.3321/j.issn:0001-5733.2007.01.040

LIU Sixin and ZENG Zhaofa. Numerical simulation for Ground Penetrating Radar wave propagation in the dispersive medium[J]. Chinese Journal of Geophysics, 2007, 50(1): 320–326. doi: 10.3321/j.issn:0001-5733.2007.01.040

冯德山, 杨良勇, 王珣. 探地雷达FDTD数值模拟中不分裂卷积完全匹配层对倏逝波的吸收效果研究[J]. 地球物理学报, 2016, 59(12): 4733–4746. doi: 10.6038/cjg20161232

FENG Deshan, YANG Liangyong, and WANG Xun. The unsplit convolutional perfectly matched layer absorption performance analysis of evanescent wave in GPR FDTD forward modeling[J]. Chinese Journal of Geophysics, 2016, 59(12): 4733–4746. doi: 10.6038/cjg20161232

底青云, 王妙月. 雷达波有限元仿真模拟[J]. 地球物理学报, 1999, 42(6): 818–825. doi: 10.3321/j.issn:0001-5733.1999.06.012

DI Qingyun and WANG Miaoyue. 2D finite element modeling for radar wave[J]. Chinese Journal of Geophysics, 1999, 42(6): 818–825. doi: 10.3321/j.issn:0001-5733.1999.06.012

杜华坤, 冯德山, 汤井田. 基于Delaunay三角形的非结构化有限元GPR正演[J]. 中南大学学报: 自然科学版, 2015, 46(4): 1326–1334. doi: 10.11817/j.issn.1672-7207.2015.04.022

DU Huakun, FENG Deshan, and TANG Jingtian. GPR simulation by finite element method of unstructured grid based on Delaunay triangulation[J]. Journal of Central South University:Science and Technology, 2015, 46(4): 1326–1334. doi: 10.11817/j.issn.1672-7207.2015.04.022

石明, 冯德山, 王洪华, 等. 各向异性介质GPR非结构化网格有限元正演[J]. 中南大学学报: 自然科学版, 2016, 47(5): 1660–1667. doi: 10.11817/j.issn.1672-7207.2016.05.027

SHI Ming, FENG Deshan, WANG Honghua, et al. GPR numerical simulation for anisotropic medium by using finite element method based on unstructured meshes[J]. Journal of Central South University:Science and Technology, 2016, 47(5): 1660–1667. doi: 10.11817/j.issn.1672-7207.2016.05.027

王洪华, 吕玉增, 王敏玲, 等. 基于PML边界条件的二阶电磁波动方程GPR时域有限元模拟[J]. 地球物理学报, 2019, 62(5): 1929–1941. doi: 10.6038/cjg2019M0610

WANG Honghua, LÜ Yuzeng, WANG Minling, et al. A perfectly matched layer for second order electromagnetic wave simulation of GPR by finite element time domain method[J]. Chinese Journal of Geophysics, 2019, 62(5): 1929–1941. doi: 10.6038/cjg2019M0610

孟旭, 刘四新, 傅磊, 等. 基于对数目标函数的跨孔雷达频域波形反演[J]. 地球物理学报, 2016, 59(5): 1875–1887. doi: 10.6038/cjg20160530

MENG Xu, LIU Sixin, FU Lei, et al. Frequency domain waveform inversion of cross-hole GPR data based on a logarithmic objective function[J]. Chinese Journal of Geophysics, 2016, 59(5): 1875–1887. doi: 10.6038/cjg20160530

戴世坤, 王顺国, 张钱江, 等. 频率域可控源电磁法2.5D正反演[J]. 中国有色金属学报, 2013, 23(9): 2513–2523. doi: 10.19476/j.ysxb.1004.0609.2013.09.022

DAI Shikun, WANG Shunguo, ZHANG Qianjiang, et al. 2.5D forward and inversion of CSEM in frequency domain[J]. The Chinese Journal of Nonferrous Metals, 2013, 23(9): 2513–2523. doi: 10.19476/j.ysxb.1004.0609.2013.09.022

薛东川, 戴世坤. 频率域2.5维电磁测深有限元模拟中的吸收边界条件[J]. 中国石油大学学报: 自然科学版, 2008, 32(6): 57–61. doi: 10.3321/j.issn:1673-5005.2008.06.011

XUE Dongchuan and DAI Shikun. Absorbing boundary condition for simulating 2.5-D electromagnetic sounding in frequency domain by finite element method[J]. Journal of China University of Petroleum:Edition of Natural Science, 2008, 32(6): 57–61. doi: 10.3321/j.issn:1673-5005.2008.06.011

胡涂. 探地雷达2.5D频率域数值模拟[D]. [硕士论文], 中南大学, 2014.

HU Tu. Frequency domain 2.5D GPR Forward Modeling[D]. [Master dissertation], Central South University, 2014.

SCHENK O and GÄRTNER K. Solving unsymmetric sparse systems of linear equations with PARDISO[C]. International Conference on Computational Science, The Netherlands, 2002. doi: 10.1007/3-540-46080-2_37.

施引文献

期刊类型引用(5)

1.	武贤龙，包小华，陈湘生，沈俊，崔宏志. 基于gprMax的衬砌脱空三维正演分析. 深圳大学学报(理工版). 2023(02): 127-135 . 百度学术
2.	刘海，陈峻浩，孙竹妤，岳云鹏，赖思聪，孟旭. 盾构隧道壁后空洞典型GPR图像特征正演分析. 广州大学学报(自然科学版). 2023(03): 1-9 . 百度学术
3.	杜翠，王宁，刘杰，程远水，张千里，刘欢. 探地雷达铁路检测大数据多线程并行处理方法. 铁道建筑. 2022(04): 126-129 . 百度学术
4.	张群慧. 基于非交错网格频域有限差分法的探地雷达最优化正演算法研究. 实验技术与管理. 2022(12): 37-44 . 百度学术
5.	程曦，张志勇. 基于人工神经网络的复杂介质中波的传播不确定性分析方法. 电子与信息学报. 2021(12): 3662-3670 . 本站查看

其他类型引用(2)

资源附件(0)

访问统计

图(10) / 表(1)

计量

文章访问数: 2152
HTML全文浏览量: 769
PDF下载量: 105
被引次数: 7

1. 引言
2. 方法理论
2.1 控制方程
2.2 有限单元法
3. 数值算例
3.1 波场参数分析
3.2 正确性验证
3.3 Open MP并行测试
3.4 复杂模型算例
4. 结论

姓名
邮箱
手机号码
标题
留言内容
验证码

留言板

探地雷达频率域2.5维正演

doi: 10.11999/JEIT190988

通讯作者:
欧阳振崇　oyzc_wy@163.com

计量

Frequency Domain 2.5D GPR Forward Modeling

1. 引言

2. 方法理论

2.1 控制方程

2.2 有限单元法

3. 数值算例

3.1 波场参数分析

3.2 正确性验证

3.2.1 全空间模型

3.2.2 半空间模型

3.3 Open MP并行测试

3.4 复杂模型算例

4. 结论

期刊类型引用(5)

其他类型引用(2)

计量

目录

1. 引言

2. 方法理论

2.1 控制方程

2.2 有限单元法

3. 数值算例

3.1 波场参数分析

3.2 正确性验证

3.3 Open MP并行测试

3.4 复杂模型算例

4. 结论

留言板

探地雷达频率域2.5维正演

doi: 10.11999/JEIT190988

通讯作者: 欧阳振崇 oyzc_wy@163.com

计量

出版历程

Frequency Domain 2.5D GPR Forward Modeling

1. 引言

2. 方法理论

2.1 控制方程

2.2 有限单元法

3. 数值算例

3.1 波场参数分析

3.2 正确性验证

3.2.1 全空间模型

3.2.2 半空间模型

3.3 Open MP并行测试

3.4 复杂模型算例

4. 结论

期刊类型引用(5)

其他类型引用(2)

计量

出版历程

目录

1. 引言

2. 方法理论

2.1 控制方程

2.2 有限单元法

3. 数值算例

3.1 波场参数分析

3.2 正确性验证

3.3 Open MP并行测试

3.4 复杂模型算例

4. 结论

通讯作者:
欧阳振崇　oyzc_wy@163.com