Reliable Deployment Algorithm of Service Function Chain Based on Deep Reinforcement Learning
-
摘要:
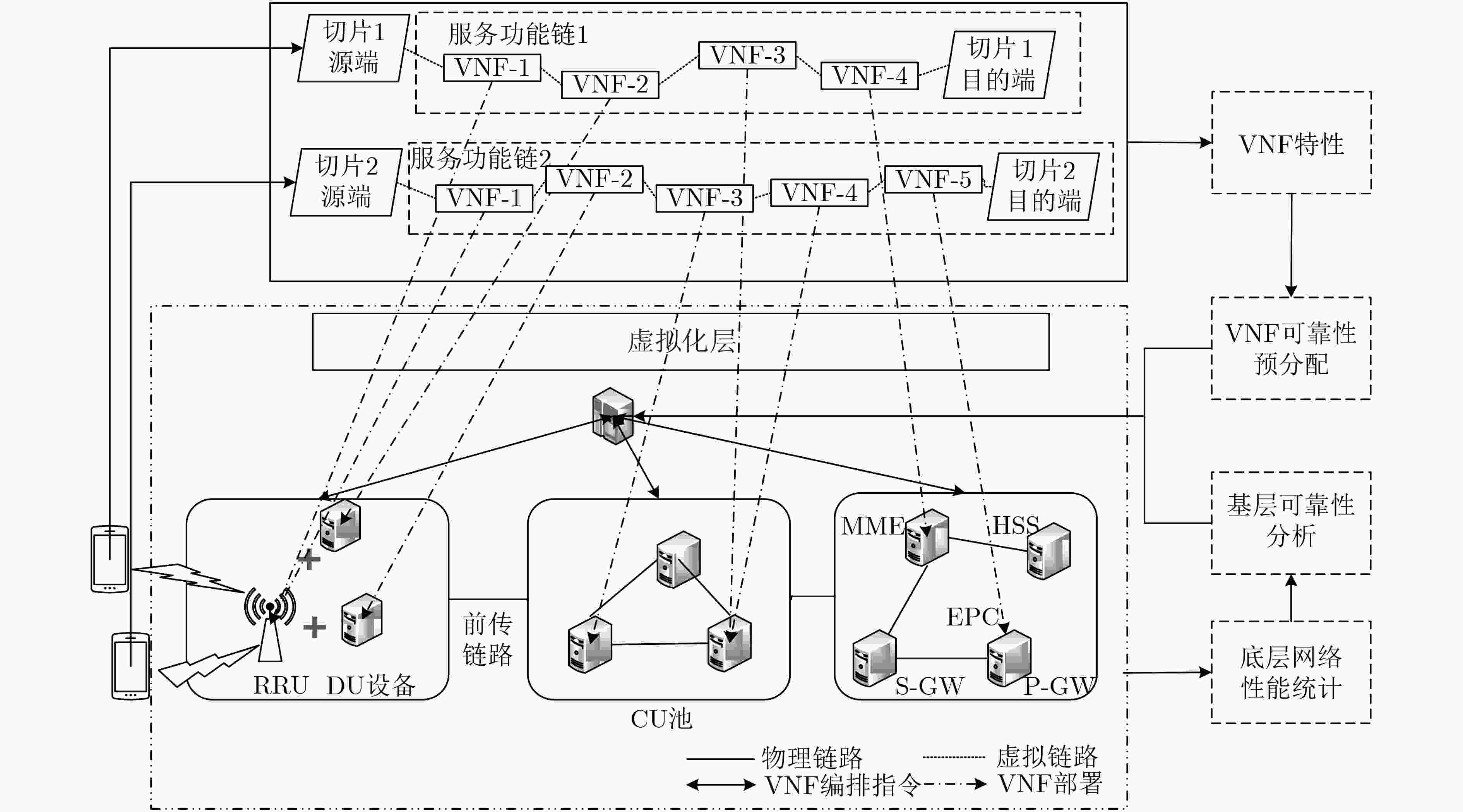
针对当前关于服务功能链(SFC)的部署问题都未考虑到虚拟网络功能(VNF)的失效重要度,该文提出了基于深度强化学习的SFC可靠部署算法。首先建立VNF和虚拟链路可靠映射模型,为重要的VNF设置高可靠性需求,并通过链路部署长度限制尽可能保证虚拟链路可靠性需求。其次,以负载均衡为资源协调原则,与VNF可靠性联合优化,最终使用深度强化学习得到服务功能链部署策略。另外,提出了基于重要度的节点备份和链路备份策略,用于应对部署过程中VNF/链路可靠性难以满足的情况。仿真结果表明,该文的可靠部署算法在保证可靠性需求的基础上能够有效减少SFC失效损失,同时使虚拟网络更加稳定可靠。
Abstract:In view of the current deployment of the Service Function Chain (SFC), the failure importance of the Virtual Network Function (VNF) is not considered,an SFC reliable deployment algorithm based on deep reinforcement learning is proposed. Firstly, a reliable mapping model of VNF and virtual links is establised, high reliability requirements is set for important VNFs, and the reliability requirements of virtual links is ensured as much as possible through link deployment length restrictions. Secondly, taking load balancing as the resource coordination principle, joint optimization the VNF reliability is jointly optimized. Finally, the deep reinforcement learning is used to get the service function chain deployment strategy. In addition, node backup and link backup strategies based on importance are proposed to deal with situations where VNF/link reliability is difficult to meet during deployment. Simulation results show that the reliable deployment algorithm in this paper can effectively reduce the failure SFC loss on the basis of ensuring the reliability requirements, and at the same time make the virtual network more stable and reliable.
-
表 1 基于深度强化学习的服务功能链可靠部署算法
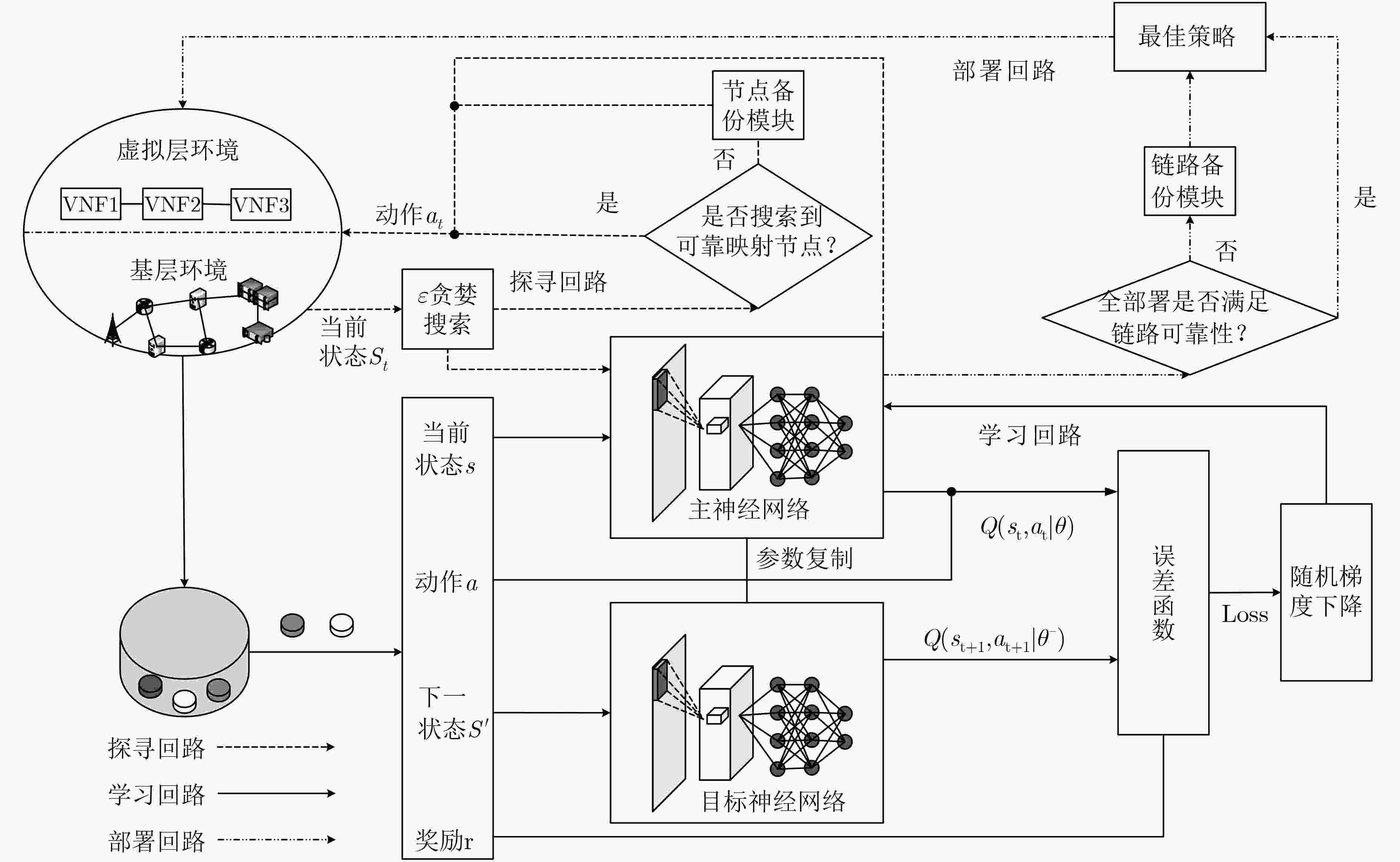
算法1 基于深度强化学习的服务功能链可靠部署算法 经验回放池初始化为空,随机初始化主网络的参数,并复制给目标网络,探寻环境信息基于式(6)~式(9)得到${w_I}$,${u'_k}$ for episode=1, 2, ···, E do 初始化状态为${{{s}}_1} = \{ {{{B}}_{{\rm{left}}}}{{,}}{{{C}}_{{\rm{left}}}}{{,}}{{{b}}_{{\rm{map}}}}{{,}}{{{c}}_{{\rm{map}}}}\} $, ${{{b}}_{{\rm{map}}}}{{,}}{{{c}}_{{\rm{map}}}}$为空 for t=1,2…D do 确定可选动作集${N'_{k{n_i}}}$, ${N''_{k{n_i}}}$随机产生0到1的数$\tau $ if $\tau < \varepsilon $:先从${ {{N'} }_{k{n_i} } }$中选择动作${a_t}$,若为空则根据算法2在${ {{N''} }_{k{n_i} } }$中选择${a_t}$,都无动作选择则${a_t}$为空 else:依据主神经网络估值${\pi ^*}(s) = {{\arg }}\max\limits_{a'} Q({{{s}}_t},{{{a'}}_t})$选取动作。end if 执行动作${{{a}}_t}$,获得奖励${r_t}$、下一状态${{{s}}_{t + 1}}$,将向量$[{{{s}}_t},{{{a}}_t},{r_t},{{{s}}_{t + 1}}]$放入经验回放池。 随机取出小批量样本向量$[{{{s}}_t},{{{a}}_t},{r_t},{{{s}}_{t + 1}}]$组成样本向量集${\upsilon _t}$ for $[{{{s}}_t},{{{a}}_t},{r_t},{{{s}}_{t + 1}}]$ in ${\upsilon _t}$ do $L{{(}}\theta {{)}} = {(\tilde Q({{{s}}_t},{{{a}}_t}|{\theta ^ - }) - Q({{{s}}_t},{{{a}}_t}|\theta ))^2}$,$\theta \leftarrow \theta - {\lambda _{{\rm{SGD}}}}\nabla L(\theta )$ end for 在θ更新T次后将主网络参数复制给目标网络。end for end for 通过主网络得到每个VNF的策略${\pi ^*}(s)$ if累计奖励$Q({s_t},{a_t}) < - 100$:拒绝该请求 else if 部署结果不满足链路可靠性需求:执行算法3 end if 表 2 基于虚拟网络功能重要度节点备份算法
算法2:基于虚拟网络功能重要度的节点备份算法 初始化节点部署方案$g'(v_I^k)$为空 repeat: if ${\omega _I} < 1/D$:搜寻${N''_{k{n_i}}}$已作为备份节点的节点集$V_{I'}^k$ if $V_{I'}^k$非空:$g'(v_I^k)$←从$V_{I'}^k$中寻找备份节点,从${{{N''}}_{k{n_i}}}/V_{I'}^k$中寻
找部署节点else:$g'(v_I^k)$←从${N''_{k{n_i}}}$中选出2个节点。可靠性最高的为部署节
点,另一备份。endifelse:$g'(v_I^k)$←从${N''_{k{n_i}}}$中选出2个节点。可靠性最高的为部署节
点,另一备份。endifuntil $RN(g'(v_I^k)) > {(R_k^{{\rm{req}}})^{{w_I}}}$or 已遍历所有组合 return 节点部署方案$g'(v_I^k)$ 表 3 基于链路备份重要度的链路备份算法
算法3:基于链路备份重要度的链路备份算法 基于$\gamma _{I,J}^k$对虚拟链路链路$l_{I,J}^k \in L_v^k$排序 for 排过序的链路链路$l_{I,J}^k \in L_v^k$ if 链路可靠性不满足: 确定$l_{I,J}^k$映射的段物理起始节点${n_i}$和终止节点${n_j}$:${p_{I,J}}$ $p{{ = \{ }}{\ell _{i,j}}|{L'_{k{l_{i,j}}}}/{p_{I,J}}\} $,部署方案增加链路P else: break end for return 部署方案 -
AYOUBI S, ZHANG Yanhong, and ASSI C. A reliable embedding framework for elastic virtualized services in the cloud[J]. IEEE Transactions on Network and Service Management, 2016, 13(3): 489–503. doi: 10.1109/TNSM.2016.2581484 汤红波, 邱航, 游伟, 等. 基于联合备份的服务功能链可靠性保障的部署方法[J]. 电子与信息学报, 2019, 41(12): 3006–3013. doi: 10.11999/JEIT190013TANG Hongbo, QIU Hang, YOU Wei, et al. A reliability-guarantee method for service function chain deployment based on joint backup[J]. Journal of Electronics &Information Technology, 2019, 41(12): 3006–3013. doi: 10.11999/JEIT190013 季新生, 赵硕, 艾健健, 等. 异构备份式的虚拟网映射方法研究[J]. 电子与信息学报, 2018, 40(5): 1087–1093. doi: 10.11999/JEIT170730JI Xinsheng, ZHAO Shuo, AI Jianjian, et al. Research on heterogeneous-backup virtual network embedding[J]. Journal of Electronics &Information Technology, 2018, 40(5): 1087–1093. doi: 10.11999/JEIT170730 POURVALI M, BAI Hao, CRICHIGNO J, et al. Multicast virtual network services embedding for improved disaster recovery support[J]. IEEE Communications Letters, 2018, 22(7): 1362–1365. doi: 10.1109/LCOMM.2018.2822739 SUN Jian, ZHU Guangyang, SUN Gang, et al. A reliability-aware approach for resource efficient virtual network function deployment[J]. IEEE Access, 2018, 6: 18238–18250. doi: 10.1109/ACCESS.2018.2815614 DINH N T and KIM Y. An efficient reliability guaranteed deployment scheme for service function chains[J]. IEEE Access, 2019, 7: 46491–46505. doi: 10.1109/ACCESS.2019.2908185 刘光远, 安秀芳, 苏森. 基于节点可靠性感知和共享路径保护的虚拟网映射算法研究[J]. 通信学报, 2016, 37(8): 51–57. doi: 10.11959/j.issn.1000-436x.2016155LIU Guangyuan, AN Xiufang, and SU Sen. Virtual network mapping algorithm with node reliability awareness and shared-path protection[J]. Journal on Communications, 2016, 37(8): 51–57. doi: 10.11959/j.issn.1000-436x.2016155 European Telecommunications Standards Institute. Network Functions Virtualisation (NFV); Reliability; Report on models and features for end-to-end reliability[R]. ETSI GS NFV-REL 003 V1.1.1, 2016. TANG Xiaoyong, LI Kenli, QIU Meikang, et al. A hierarchical reliability-driven scheduling algorithm in grid systems[J]. Journal of Parallel and Distributed Computing, 2012, 72(4): 525–535. doi: 10.1016/j.jpdc.2011.12.004 BIJWE S, MACHIDA F, ISHIDA S, et al. End-to-End reliability assurance of service chain embedding for network function virtualization[C]. 2017 IEEE Conference on Network Function Virtualization and Software Defined Networks (NFV-SDN), Berlin, Germany, 2017: 1–4. doi: 10.1109/NFV-SDN.2017.8169853. KUO Tungwei, LIOU B Hheng, LIN K C J, et al. Deploying Chains of virtual network functions: On the relation between link and server usage[J]. IEEE/ACM Transactions on Networking, 2018, 26(4): 1562–1576. doi: 10.1109/TNET.2018.2842798 魏亮, 黄韬, 张娇, 等. 基于强化学习的服务链映射算法[J]. 通信学报, 2018, 39(1): 90–100. doi: 10.11959/j.issn.1000-436x.2018002WEI Liang, HUANG Tao, ZHANG Jiao, et al. Service Chain mapping algorithm based on reinforcement learning[J]. Journal on Communications, 2018, 39(1): 90–100. doi: 10.11959/j.issn.1000-436x.2018002 CAO Haotong, ZHU Yongxu, ZHENG Gan, et al. A novel optimal mapping algorithm with less computational complexity for virtual network embedding[J]. IEEE Transactions on Network and Service Management, 2018, 15(1): 356–371. doi: 10.1109/TNSM.2017.2778106 ZHANG Xin, QIAN Zhuzhong, ZHANG Sheng, et al. Pattern-aware reliable virtual network function chain deployment[C]. 2017 IEEE International Symposium on Parallel and Distributed Processing with Applications and 2017 IEEE International Conference on Ubiquitous Computing and Communications (ISPA/IUCC), Guangzhou, China, 2017: 335–342. doi: 10.1109/ISPA/IUCC.2017.00055. SHAHRIAR N, AHMED R, CHOWDHURY S R, et al. Generalized recovery from node failure in virtual network embedding[J]. IEEE Transactions on Network and Service Management, 2017, 14(2): 261–274. doi: 10.1109/TNSM.2017.2693404 -





 下载:
下载:


 下载:
下载:
