一种基于正交调制的新型降噪差分混沌键控系统

张刚; 刘金惠; 张天骐

doi:10.11999/JEIT190955

一种基于正交调制的新型降噪差分混沌键控系统

doi: 10.11999/JEIT190955

重庆邮电大学通信与信息工程学院重庆 400065

基金项目: 国家自然科学基金(61771085, 61371164)，重庆市教育委员会科研项目(KJQN201900601)

详细信息

作者简介:
张刚：男，1976年生，博士，教授，研究方向为混沌同步、混沌保密通信

刘金惠：女，1996年生，硕士生，研究方向为混沌保密通信

张天骐：男，1971年生，博士后，教授，研究方向为扩频信号的盲处理、神经网络实现以及信号的同步处理

通讯作者:
刘金惠　1342343570@qq.com

中图分类号: TN911.3
计量
- 文章访问数: 949
- HTML全文浏览量: 276
- PDF下载量: 64
- 被引次数: 0
出版历程
- 收稿日期: 2019-11-25
- 修回日期: 2020-09-15
- 网络出版日期: 2020-12-08
- 刊出日期: 2021-02-23

A Novel Noise Reduction Differential Chaos Shift Keying System Based on Quadrature Modulation

School of Communication and Information Engineering, Chongqing University of Posts and Telecommunications (CQUPT), Chongqing 400065, China

Funds: The National Natural Science Foundation of China (61771085, 61371164), The Research Project of Chongqing Educational Commission (KJQN201900601)

摘要

摘要:
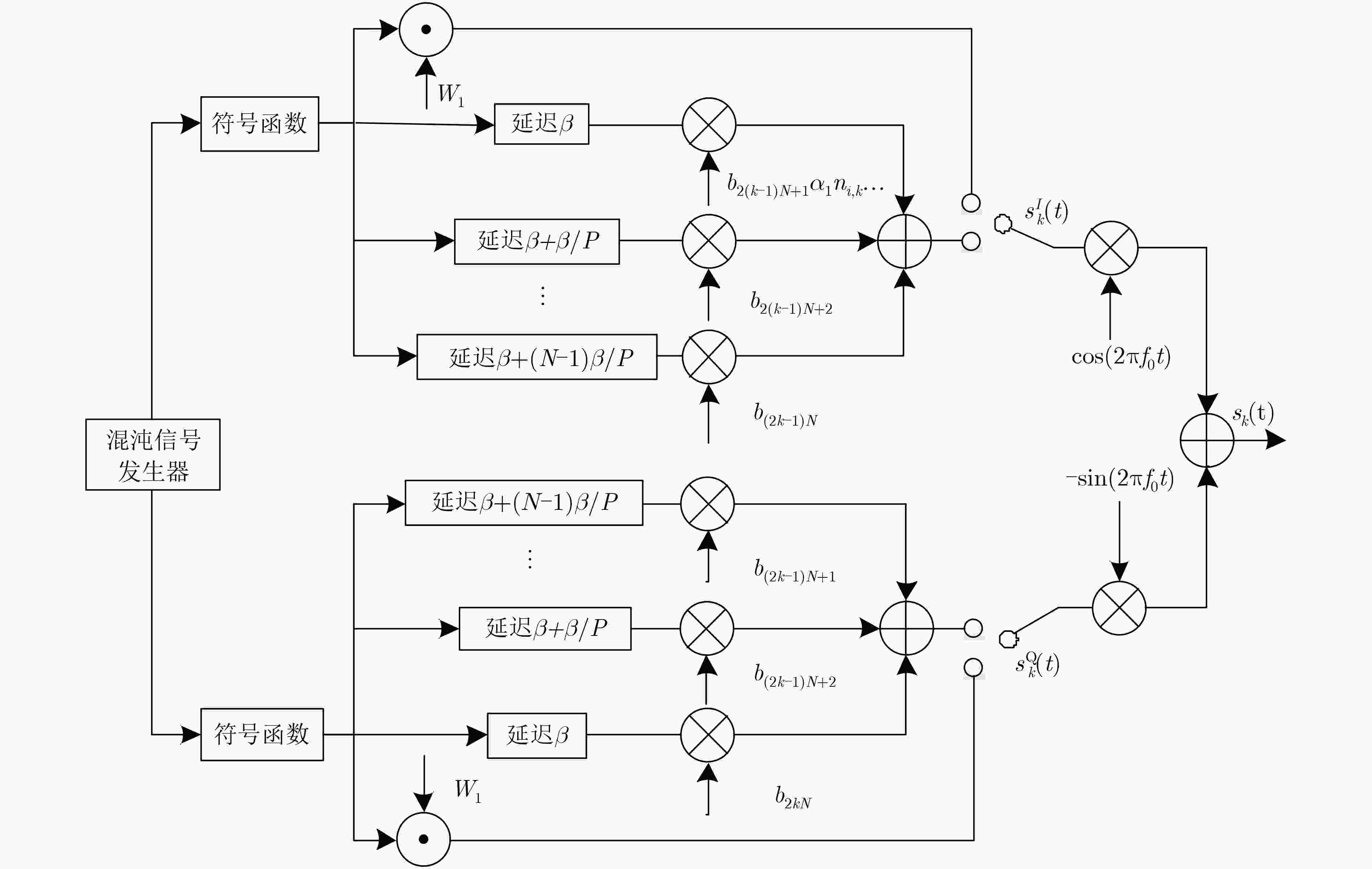
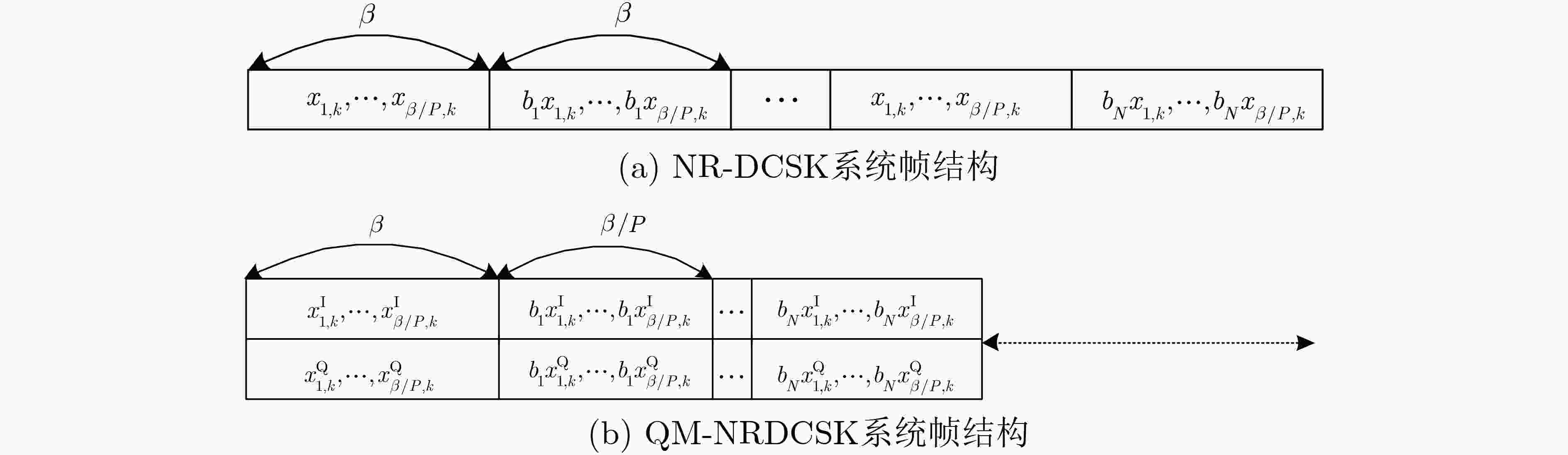
针对降噪差分混沌键控(NR-DCSK)传输速率低的缺点，该文提出一种基于正交调制的新型降噪差分混沌键控(QM-NRDCSK)系统。发生器产生两路混沌序列，每一路的参考信号是信息承载信号的
\begin{document}$P$\end{document}
次重复，不同用户信息通过不同时隙区分，两路信号使用正交调制在相同频带上传输。接收端通过滑动平均滤波器对每一路的参考信号进行
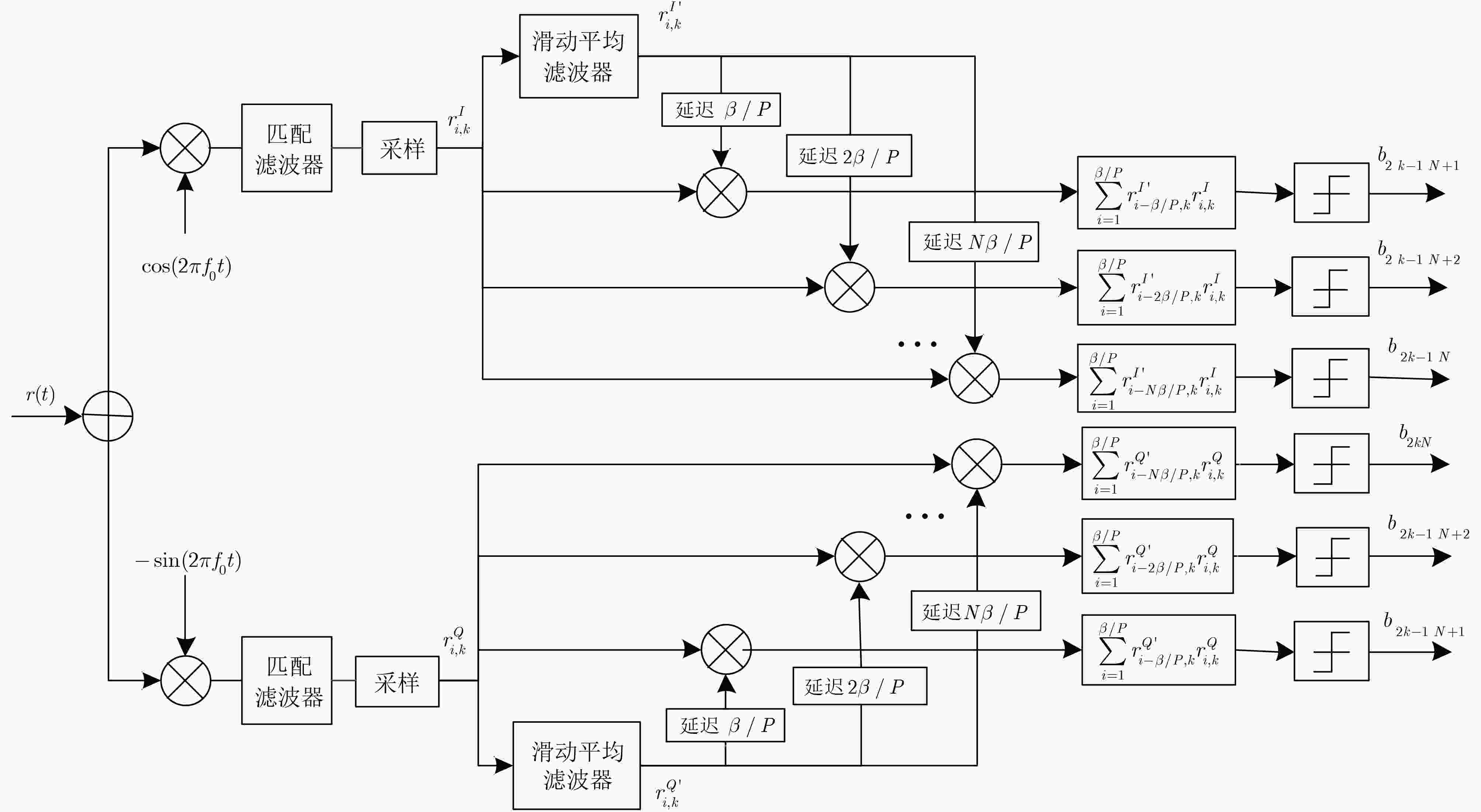
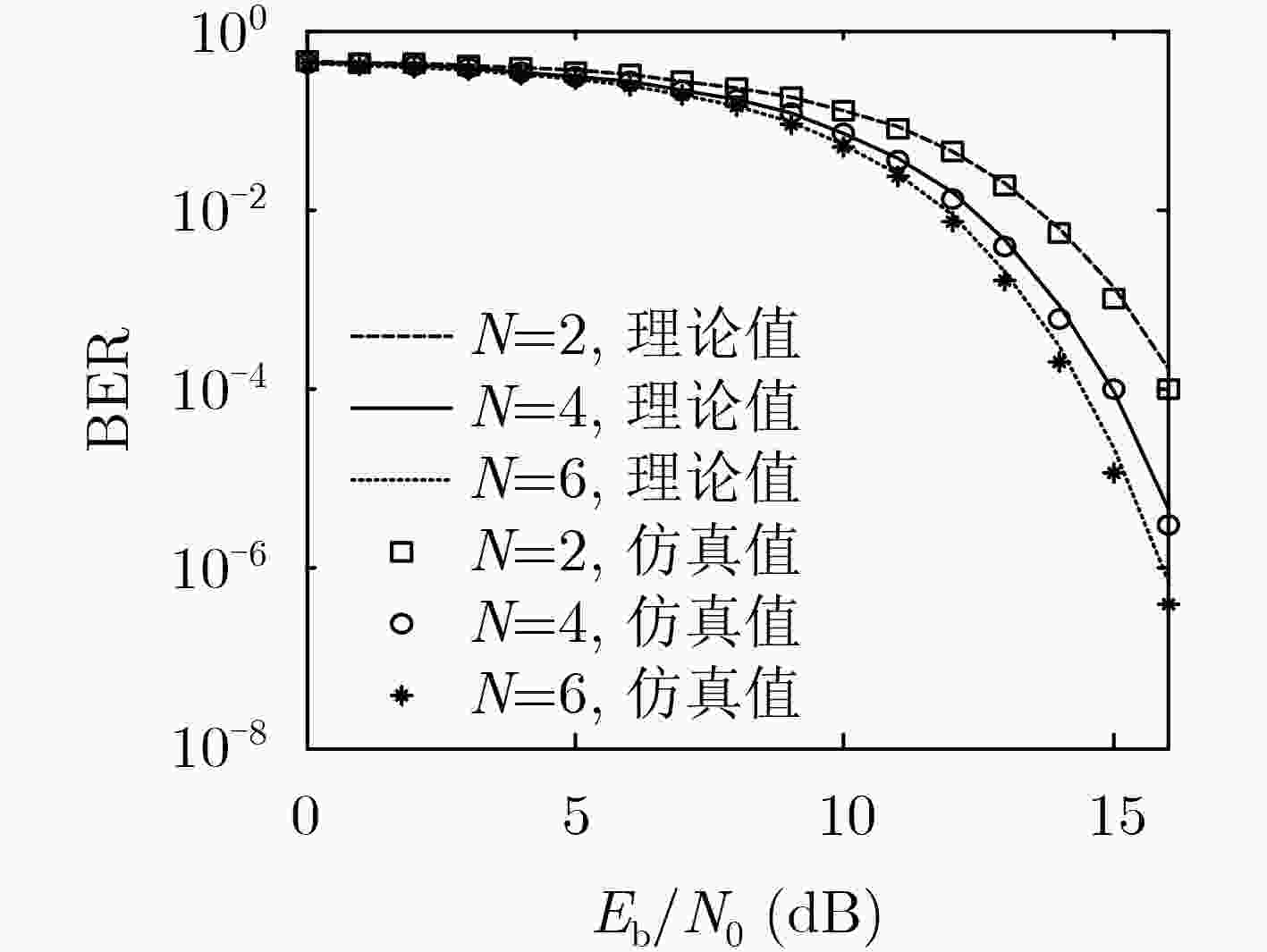
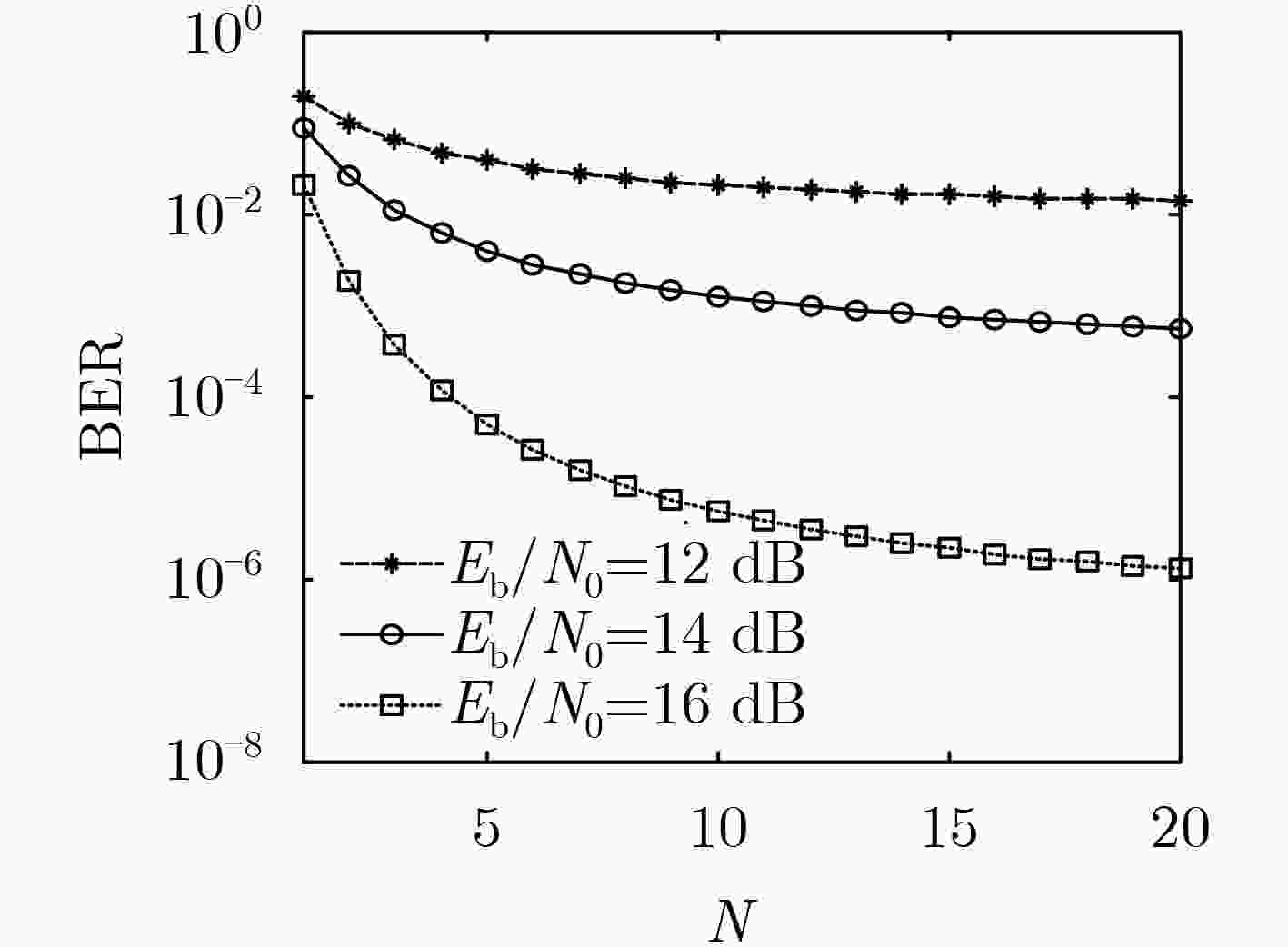
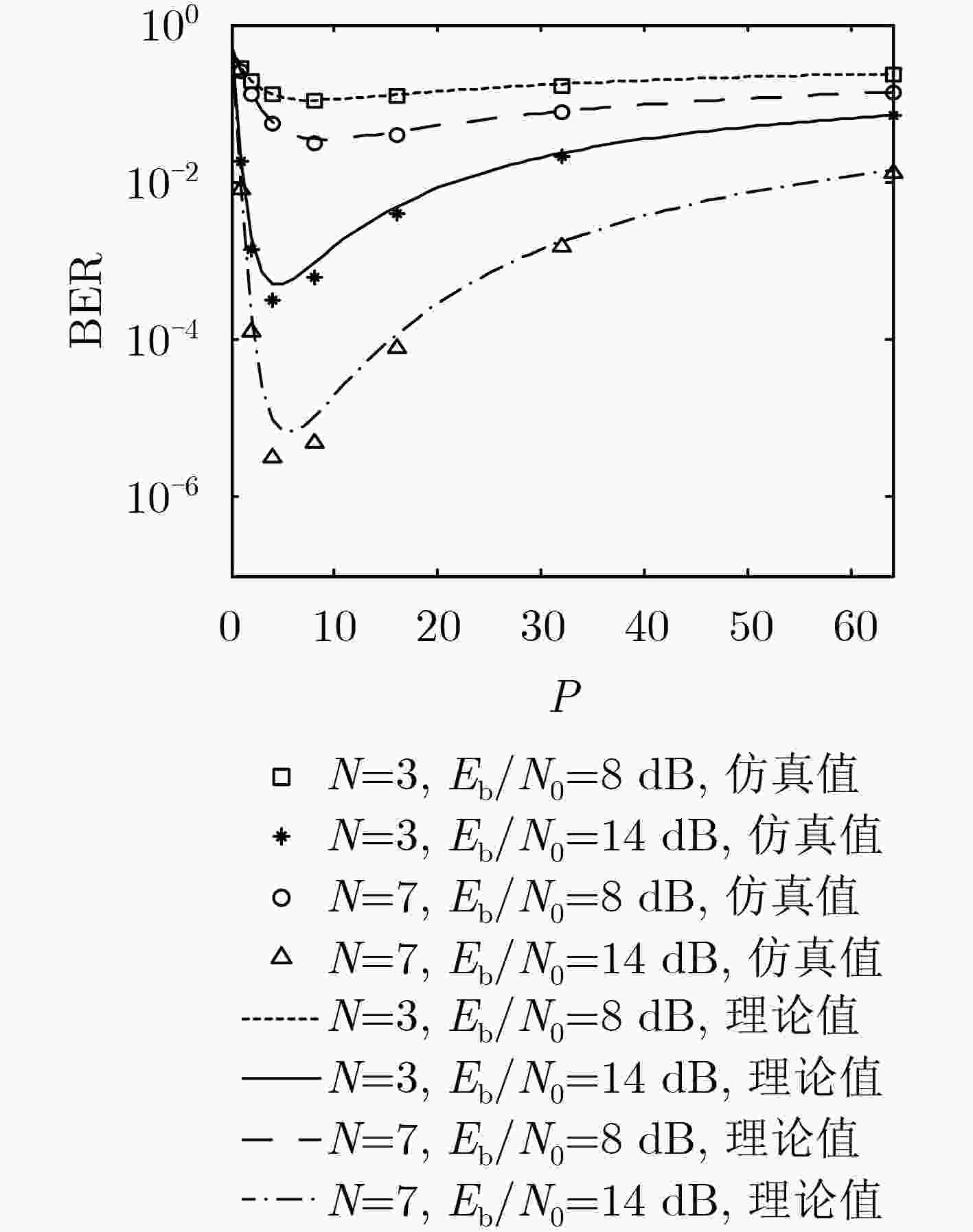
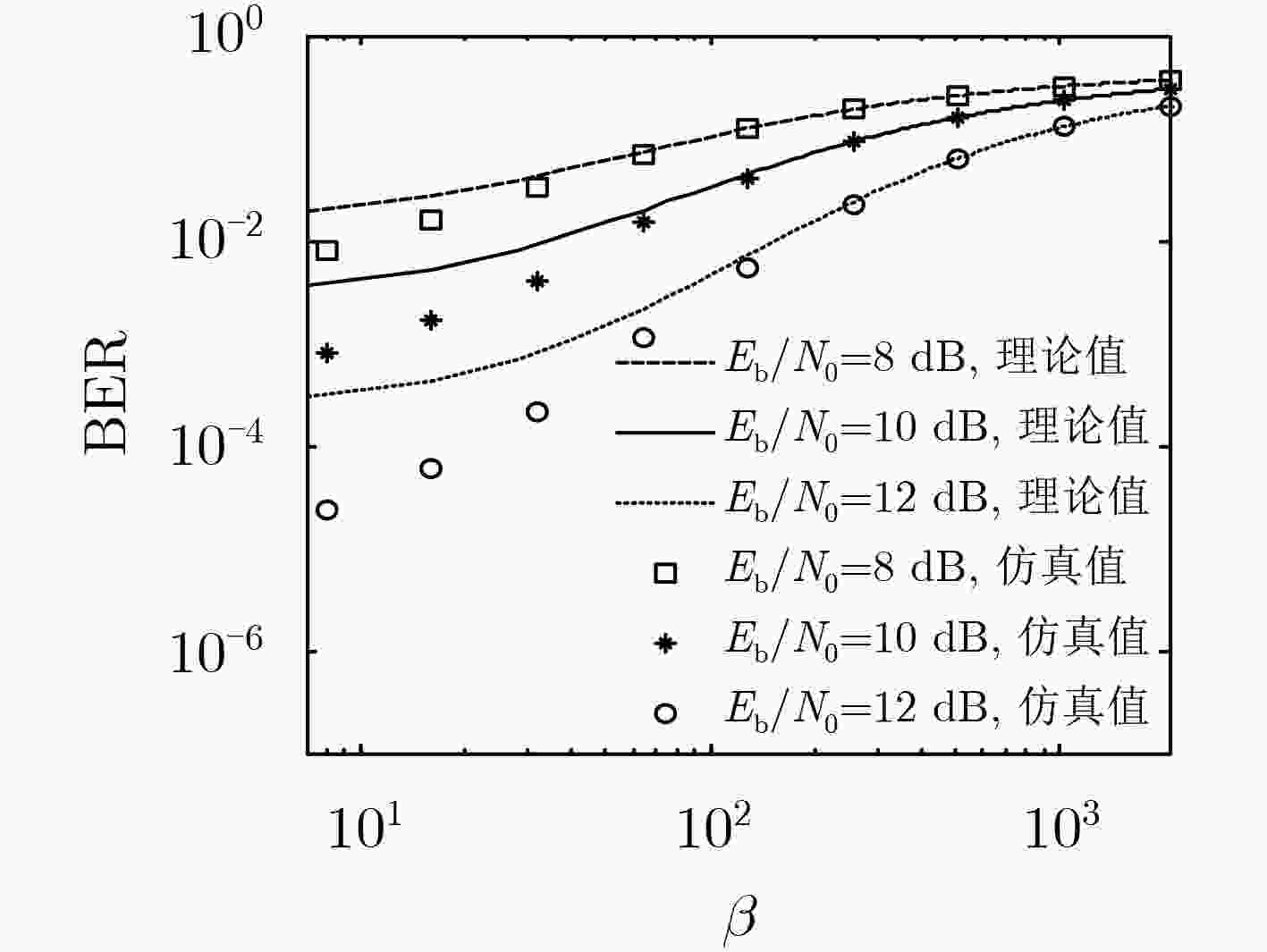
次平均后与信息信号进行非相干解调。通过在AWGN和多径Rayleigh衰落信道下的仿真，验证了理论推导的正确性，并表明该系统在具有较高频谱利用率的同时，能有效提高传输速率且拥有较好的误码性能。
- 差分混沌键控 /
- 滑动平均滤波器 /
- 降噪 /
- 传输速率 /
- 比特误码率
Abstract:
To overcome the shortcomings of low transmission rate of Noise Reduction Differential Chaos Shift Keying (NR-DCSK), a novel Noise Reduction Differential Chaos Shift Keying system based on Quadrature Modulation (QM-NRDCSK) is proposed. The generator generates two chaotic sequences, the reference signal of each channel is P-time repetition of the information-bearing signal. The information of different users is distinguished by different time slots, and the two signals are transmitted on the same frequency band by using quadrature modulation. The reference signal of each channel is averaged P times by the moving average filter at the receiving end, and then non-coherently demodulated with the information signal. The correctness of the theoretical derivation is verified by simulations in AWGN and multi-path Rayleigh fading channels, and it shows that the system can effectively improve the transmission rate and has better bit error performance while having high spectrum utilization.
- Differential Chaos Shift Keying (DCSK) /
- Moving average filter /
- Noise reduction /
- Transmission rate /
- Bit Error Rate (BER)

HTML全文

图 1 QM-NRDCSK系统第$k$帧发送端框图

下载: 全尺寸图片幻灯片

图 2 QM-NRDCSK系统第$k$帧接收端框图

下载: 全尺寸图片幻灯片

图 3 多径Rayleigh信道模型

下载: 全尺寸图片幻灯片

图 4 系统帧结构

下载: 全尺寸图片幻灯片

图 5 不同$N$值下系统BER随${E_{\rm{b}}}/{N_0}$变化曲线

下载: 全尺寸图片幻灯片

图 6 不同${E_{\rm{b}}}/{N_0}$下系统BER随$N$值变化曲线

下载: 全尺寸图片幻灯片

图 7 不同$P$值下系统BER随${E_{\rm{b}}}/{N_0}$变化曲线

下载: 全尺寸图片幻灯片

图 8 不同$N$值下系统BER随$P$变化曲线

下载: 全尺寸图片幻灯片

图 9 不同信噪比下系统BER随$\beta $变化曲线

下载: 全尺寸图片幻灯片

图 10 不同路径下系统BER随${E_{\rm{b}}}/{N_0}$变化曲线

下载: 全尺寸图片幻灯片

图 11 不同信道增益下系统BER随${E_{\rm{b}}}/{N_0}$变化曲线

下载: 全尺寸图片幻灯片

图 12 Rayleigh信道下不同系统误码性能对比

下载: 全尺寸图片幻灯片

参考文献(20)

KADDOUM G, TRAN H V, KONG Long, et al. Design of simultaneous wireless information and power transfer scheme for short reference DCSK communication systems[J]. IEEE Transactions on Communications, 2017, 65(1): 431–443. doi: 10.1109/TCOMM.2016.2619707

张琳, 徐位凯, 王琳, 等. 码复用差分混沌键控性能分析与同步算法[J]. 重庆邮电大学学报: 自然科学版, 2016, 28(3): 330–336. doi: 10.3979/j.issn.1673-825X.2016.03.008

ZHANG Lin, XU Weikai, WANG Lin, et al. Performance analysis and synchronization algorithm for CS-DCSK system[J]. Journal of Chongqing University of Posts and Telecommunications:Natural Science Edition, 2016, 28(3): 330–336. doi: 10.3979/j.issn.1673-825X.2016.03.008

HU Wei, WANG Lin, and KADDOUM G. Design and performance analysis of a differentially spatial modulated chaos shift keying modulation system[J]. IEEE Transactions on Circuits and Systems II: Express Briefs, 2017, 64(11): 1302–1306. doi: 10.1109/TCSII.2017.2697456

KADDOUM G, SOUJERI E, ARCILA C, et al. I-DCSK: An improved noncoherent communication system architecture[J]. IEEE Transactions on Circuits and Systems II: Express Briefs, 2015, 62(9): 901–905. doi: 10.1109/TCSII.2015.2435831

LIU Lidong, LI Yi, ZHANG Zhaolun, et al. High-efficiency and noise-robust DCSK approach based on an analytically solvable chaotic oscillator[J]. Electronics Letters, 2018, 54(24): 1384–1385. doi: 10.1049/el.2018.6054

YANG Hua and JIANG Guoping. Reference-modulated DCSK: A novel chaotic communication scheme[J]. IEEE Transactions on Circuits and Systems II: Express Briefs, 2013, 60(4): 232–236. doi: 10.1109/TCSII.2013.2251949

FANG Yi, XU Jing, WANG Lin, et al. Performance of MIMO relay DCSK-CD systems over Nakagami fading channels[J]. IEEE Transactions on Circuits and Systems I: Regular Papers, 2013, 60(3): 757–767. doi: 10.1109/TCSI.2012.2215755

LEE T F. Enhancing the security of password authenticated key agreement protocols based on chaotic maps[J]. Information Sciences, 2015, 290: 63–71. doi: 10.1016/j.ins.2014.08.041

FANG Yi, HAN Guojun, CHEN Pingping, et al. A survey on DCSK-based communication systems and their application to UWB scenarios[J]. IEEE Communications Surveys & Tutorials, 2016, 18(3): 1804–1837. doi: 10.1109/COMST.2016.2547458

张刚, 许嘉平, 张天骐. 基于希尔伯特变换的多用户DCSK通信系统性能分析[J]. 电子与信息学报, 2018, 40(11): 2744–2751. doi: 10.11999/JEIT180110

ZHANG Gang, XU Jiaping, and ZHANG Tianqi. Performance analyze for multiuser-DCSK communication system based on Hilbert transform[J]. Journal of Electronics &Information Technology, 2018, 40(11): 2744–2751. doi: 10.11999/JEIT180110

DUAN Junyi and YANG Hua. Phase-orthogonality CDSK: A reliable and effective chaotic communication scheme[J]. IET Communications, 2018, 12(9): 1116–1122. doi: 10.1049/iet-com.2017.1239

KADDOUM G and SOUJERI E. NR-DCSK: A noise reduction differential chaos shift keying system[J]. IEEE Transactions on Circuits and Systems II: Express Briefs, 2016, 63(7): 648–652. doi: 10.1109/TCSII.2016.2532041

WANG Shaonan, LIU Yingjie, and MA Weijiao. Design of a novel frequency division scheme for DCSK chaos communication system[C]. The 3rd International Conference on Information Management (ICIM), Chengdu, China, 2017: 317–321. doi: 10.1109/INFOMAN.2017.7950400.

张刚, 陈和祥, 张天骐. 多用户正交差分混沌键控通信系统[J]. 系统工程与电子技术, 2019, 41(3): 667–673. doi: 10.3969/j.issn.1001-506X.2019.03.28

ZHANG Gang, CHEN Hexiang, and ZHANG Tianqi. Multiuser orthogonal differential chaos shift keying communication system[J]. Systems Engineering and Electronics, 2019, 41(3): 667–673. doi: 10.3969/j.issn.1001-506X.2019.03.28

CAI Guofa, FANG Yi, WEN Jinming, et al. Multi-carrier M-ary DCSK system with code index modulation: An efficient solution for chaotic communications[J]. IEEE Journal of Selected Topics in Signal Processing, 2019, 13(6): 1375–1386. doi: 10.1109/JSTSP.2019.2913944

QUYEN N X. Bit-error-rate evaluation of high-efficiency differential-chaos-shift-keying system over wireless channels[J]. Journal of Circuits, Systems and Computers, 2018, 27(1): 1850008. doi: 10.1142/S0218126618500081

YANG Hua, JIANG Guoping, and DUAN Junyi. Phase-separated DCSK: A simple delay-component-free solution for chaotic communications[J]. IEEE Transactions on Circuits and Systems II: Express Briefs, 2014, 61(12): 967–971. doi: 10.1109/TCSII.2014.2356914

QUYEN N X. On the study of a quadrature DCSK modulation scheme for cognitive radio[J]. International Journal of Bifurcation and Chaos, 2017, 27(9): 1750135. doi: 10.1142/S0218127417501358

YANG H, TANG W K S, CHEN Gangrong, et al. System design and performance analysis of orthogonal multi-level differential chaos shift keying modulation scheme[J]. IEEE Transactions on Circuits and Systems I: Regular Papers, 2016, 63(1): 146–156. doi: 10.1109/TCSI.2015.2510622

XU Weikai, WANG Lin, and CHEN Guanrong. Performance analysis of the CS-DCSK/BPSK communication system[J]. IEEE Transactions on Circuits and Systems I: Regular Papers, 2014, 61(9): 2624–2633. doi: 10.1109/TCSI.2014.2312477

施引文献

资源附件(0)

访问统计