A Multiobjective Evolution Strategy Algorithm for DNA Sequence Design
-
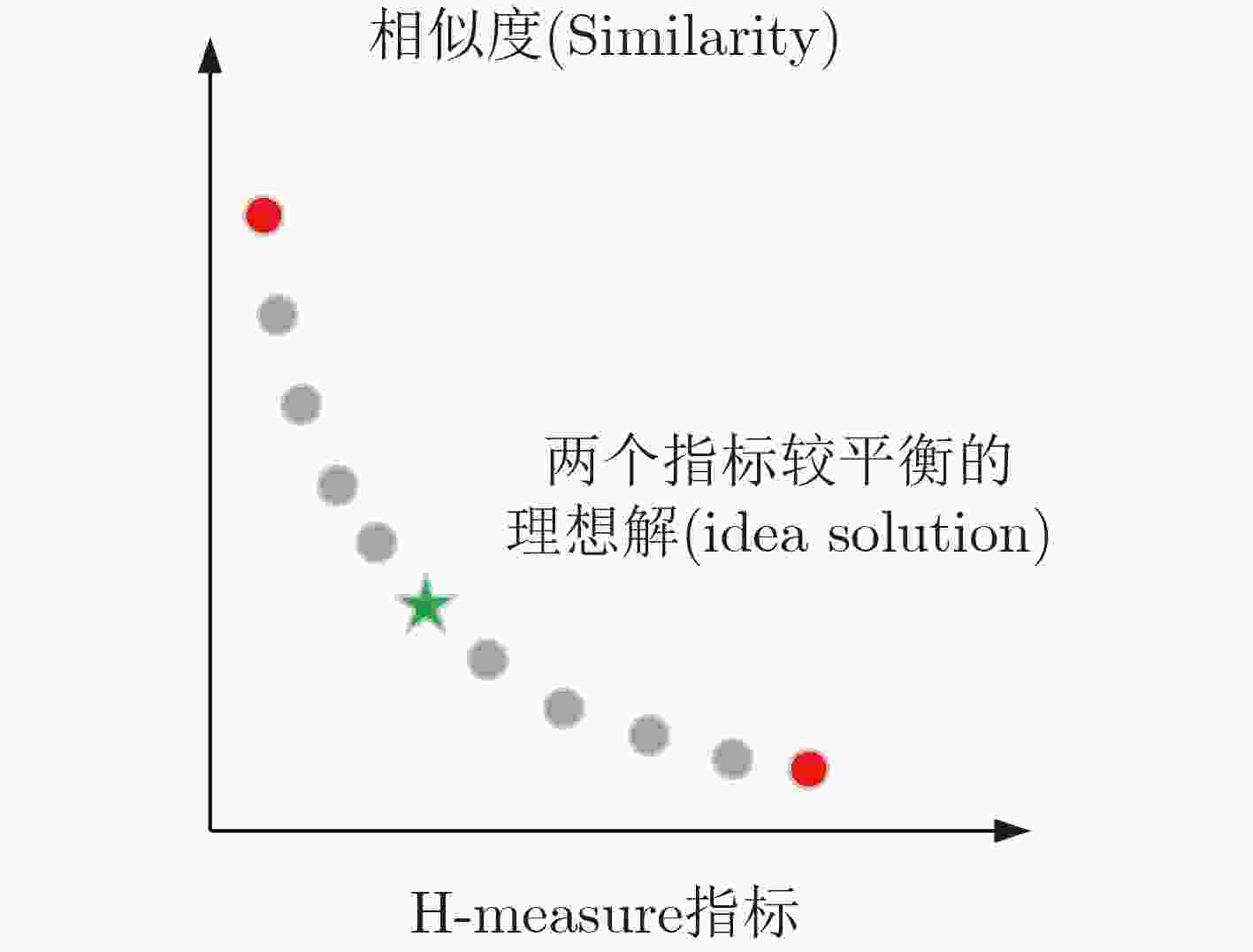
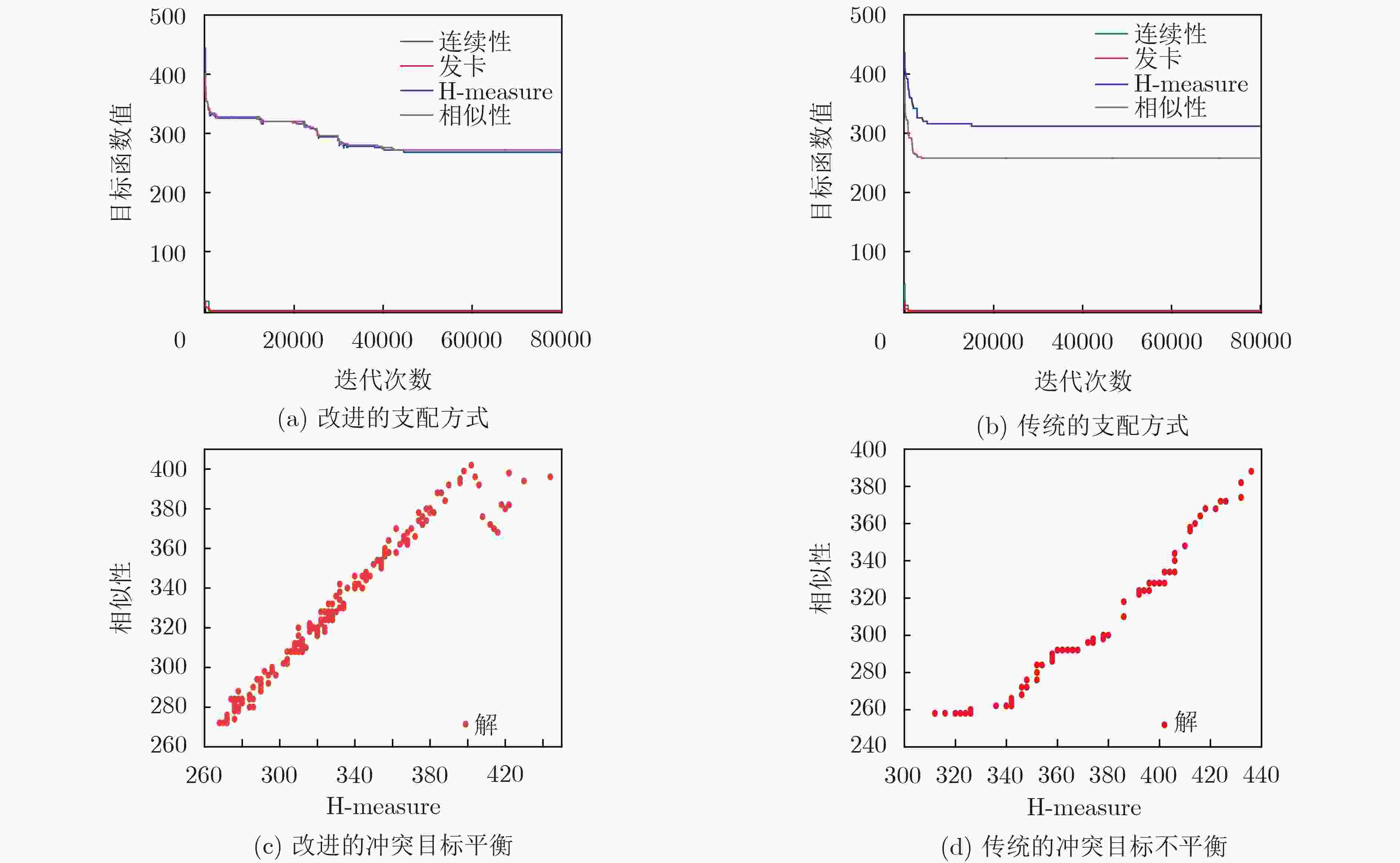
摘要: 设计高质量的核酸分子集合能有效提高DNA计算的可靠性、有效性和可求解问题的规模。DNA分子需要满足热力学约束、相似度约束、GC含量约束等多个相互冲突的目标函数,是典型的多目标优化问题。该文提出一种多目标进化策略(MOES)算法求解DNA分子序列设计问题,算法设计了随机碱基变异算子实现高效的局部搜索和全局搜索。改进的评价函数综合考虑了候选解的支配关系和冲突目标的平衡程度,选取符合DNA编码约束的核酸序列。实验结果证明,该文提出的算法具有高效的搜索效率和快速收敛能力,可以产生高质量的DNA序列集合,优于其他对比算法产生的DNA分子序列集合。Abstract: It is important to design high-quality DNA sequences set, which can improve the reliability and efficiency of DNA computing. DNA sequence design problem is an multiobjective optimization problem that needs to satisfy multiple conflict objectives which are thermodynamic constraint, similarity constraint and GC content constraint simultaneously. A MultiObjective Evolutionary Strategy (MOES) is proposed to solve the DNA sequence design problem. The random base mutation operator is designed for exploration and exploitation the search space. The fitness function is improved for obtaining balanced similarity and H-measure objective functions. Some state-of-the-art approaches are chosen to evaluate the effectivity of proposed algorithm. The experiment results show that the proposed multiobjective evolution strategy algorithm obtains very promising DNA sequences and outperforms previous approaches.
-
表 1 个体变异算子伪代码
输入: X=$5' $–x1x2$ \cdots $xn–$3' $ 输出: Y=$5' $–y1y2$ \cdots $yn–$3' $ 1: for j=1 to n 2: List.add(j) 3: end for 4: k=random(n) 5: for j=1 to k 6: i = random(List.count) 7: yi=(xi+random(3)+1) mod 4 8: List.delete(i) 9: end for 表 2 算法总体流程伪代码
1: Initialization 2: while (t < max iteration) 3: for i=1 to P 4: p = Pt(i) 5: q = Individual Mutation(p) 6: if q ≺ p then 7: Pt(i)=q 8: else if (q ⊀ p) and (p ⊀ q) then 9: if Fitness(q) > Fitness(p) then 10: Pt(i)=q 11: end if 12: end if 13: end for 14: t=t+1 15: end while 表 3 7条长度为20的DNA序列的结果比较
方法(序列) 连续性 发卡结构 H-measure 相似度 Tm GC(%) MGA[7] TAGACCACTGTTGCACATGG 0 0 58 52 50.2794 50 ATTCGGTCAGACTTGCTGTG 0 0 64 52 48.6650 50 ATAGTGCGGACAGTAGTTCC 0 0 66 59 50.1634 50 AATACGCGGAACGTAACCTC 0 0 61 85 50.4158 50 AATACGCGGAACGTAACCTC 0 0 61 85 50.4158 50 ACAGCCTTAAGCCTAACTCC 0 3 65 54 49.0641 50 ATGCTTCCGACATGGAATGG 0 3 63 57 49.8160 50 f (x) 0 6 438 444 1.7508 0 IWO[8] ACACCAGCACACCAGAAACA 9 0 55 55 48.4670 50 GTTCAATCGCCTCTCGGTAT 0 0 57 57 49.3935 50 GCTACCTCTTCCACCATTCT 0 0 55 55 49.2453 50 GAATCAATGGCGGTCAGAAG 0 0 66 66 49.9440 50 TTGGTCCGGTTATTCCTTCG 0 0 65 65 50.6418 50 CCATCTTCCGTACTTCACTG 0 0 56 56 51.0993 50 TTCGACTCGGTTCCTTGCTA 0 0 58 58 47.6049 50 f (x) 9 0 412 412 3.4944 0 pMO-ABC[10] TGTGGTTGGTTAGTCGGTTG 0 0 46 49 51.0421 50 GGTGGTATTGGTGGTATTGG 0 0 47 47 53.8027 50 CTTCTCTTCTCTTGCCGCTT 0 0 39 56 46.4112 50 AACAACCTCCACACCGAACA 0 0 62 32 49.1737 50 CTCTCTCTCTCACTCTCTCA 0 0 41 48 46.5220 50 CTCTCATTCCTTCTTACCCC 16 0 43 51 50.8283 50 TGGTGTTGCTGGTGTAGGTT 0 0 48 51 49.3985 50 f (x) 16 0 326 334 7.3915 0 MOES GGAGAGGAGAAGAAGAAGAG 0 0 52 25 48.1727 50 CCTCCACATCACCATTAACC 0 0 56 31 52.3807 50 CTCTCTCTCTCTCTCTCTCT 0 0 34 37 45.6658 50 TTCCTTCCTTCCTTCCTTCC 0 0 36 39 48.7500 50 TTGGTTGGTTGGTTGGTTGG 0 0 30 46 51.3054 50 TTGTTGTTGGTGGTGGTGGT 0 0 30 48 50.2236 50 TGTGTGTGGTGTGTGTTGTG 0 0 30 46 51.0025 50 f (x) 0 0 268 272 6.7149 0 表 4 14条长度为20的DNA序列的结果比较
方法(序列) 连续性 发卡结构 H-measure 相似度 Tm GC(%) MGA[7] CTCATCTAATCAGCCTCGCA 0 0 135 114 48.1554 50 CTAATAGTGACAGCTGCGTG 0 3 131 119 50.2421 50 GCATCGTTAGAGACACCTAC 0 3 134 124 50.7932 50 GCATCAATATGCGCGACTAC 0 0 131 125 50.2815 50 CATTAAGTAGACGCTGTCGG 0 3 132 114 50.9507 50 TATGGATGAGGAGGACCTAG 0 3 133 117 50.6387 50 CAGAGATGTTCTGTACCACC 0 3 128 117 51.2232 50 CGTCGAGAATTCGTAGCTCA 0 0 137 119 48.3224 50 TCTGTTACCGTATCGGATCG 0 3 129 115 50.8791 50 AGAAGAGTTCGACTTGCTGG 0 3 134 121 47.5507 50 GCAAGGAATTCACCGTCTGT 0 3 133 129 48.9881 50 CGTGTGAAGAGAGTGGTTCA 0 0 127 123 48.9355 50 CGACTGAATCATGGACCTGT 0 3 134 126 49.7624 50 TACCGAGAAGTAGGACTGCA 0 3 134 124 48.3847 50 f (x) 0 30 1852 1687 3.6725 0 INSGA-II[9] CGAGACATCGTGCATATCGT 0 4 143 124 49.6393 50 TATAGCACGAGTGCGCGTAT 0 3 137 130 48.5659 50 GATCTACGATCATGAGAGCG 0 4 135 126 49.6673 50 TCTGTACTGCTGACTCGAGT 0 3 163 124 47.1312 50 CGAGTAGTCACACGATGAGA 0 0 152 132 49.2836 50 AGATGATCAGCAGCGACACT 0 3 133 133 46.5546 50 TGTGCTCGTCTCTGCATACT 0 4 159 130 47.1507 50 AGACGAGTCGTACAGTACAG 0 0 152 134 49.9091 50 ATGTACGTGAGATGCAGCAG 0 0 139 121 48.9270 50 ATCACTACTCGCTCGTCACT 0 3 141 132 47.5190 50 TCAGAGATACTCACGTCACG 0 3 142 123 49.2836 50 GACAGAGCTATCAGCTACTG 0 3 129 124 49.2927 50 GCTGACATAGAGTGCGATAC 0 0 130 133 50.1725 50 ACATCGACACTACTACGCAC 0 3 133 144 50.1554 50 f (x) 0 33 1988 1810 3.6179 0 pMO-ABC[10] GTTATTGGTGGTGTGCGTTG 0 0 143 82 51.9305 50 ACGGAAGTAGGAAGGAGAGA 0 0 137 106 47.8089 50 GGAAGACGCAGAAGAGAAAG 9 0 121 110 48.2609 50 CCTCCTTATTGCCTTCCTTC 0 0 114 102 50.3081 50 AACTAACCACCGACCAACCA 0 0 95 118 50.1102 50 ACACACAACACACACACTCC 0 0 88 119 50.4577 50 ACACCACCACATTACCACAC 0 0 97 119 51.9161 50 CTTCCGTCTCTTCTCTCTCT 0 0 134 105 46.9561 50 AAGGAGCGAGGAAGCGAAAA 16 0 107 95 45.8306 50 AACACCAGAACATCCACACC 0 0 90 131 50.5474 50 CCAACACCATACAACAGACC 0 0 95 130 52.3720 50 AAGGCGGAAGGATAGAAGAG 0 0 128 115 48.5370 50 TCTGCCGCTTCTTCTTCTTC 0 0 118 95 46.4000 50 TCCTCTCGTCTATTCTCCTC 0 0 111 98 48.4427 50 f (x) 25 0 1578 1525 6.5414 0 MOES CATACACACTCACACTCACC 0 0 112 89 51.6792 50 TTGTTGTGGGTTGTCCGGTT 9 0 105 90 49.7949 50 ACACACACACACACACACAC 0 0 93 78 50.9244 50 TTGTGGTCCTGGTGTTCTCT 0 0 112 90 48.4957 50 GAGAGAGAGAGAGAGAGAGA 0 0 72 100 45.6568 50 TGGTGTGGTGTGGTTAGGTT 0 0 96 93 50.5325 50 TTGGTGGTGGTGGTTGTAGT 0 0 96 95 50.5325 50 CCAACCAACCAACCAACCAA 0 0 95 78 51.3054 50 AACAAGCCAGAAGCCAGAAG 0 0 94 102 47.5066 50 GTTGGTGCTGTTGTTGAGGT 0 0 101 99 49.4550 50 GAAGAAGGGAGGAGAGAAGA 9 0 77 108 47.4961 50 AATGGAAGCGAAGCGAAGTG 0 0 93 104 47.6766 50 AACCATCAACCGCCGAAGAA 0 3 104 95 48.1694 50 AAGGTGGAGAGGAAGGAGAA 0 0 82 111 47.4098 50 f (x) 18 3 1332 1332 6.0224 0 -
ADLEMAN L M. Molecular computation of solutions to combinatorial problems[J]. Science, 1994, 266(5187): 1021–1024. doi: 10.1126/science.7973651 DE SILVA P Y and GANEGODA G U. New trends of digital data storage in DNA[J]. BioMed Research International, 2016: 8072463. BRAICH R S, CHELYAPOV N, JOHNSON C, et al. Solution of a 20-variable 3-SAT problem on a DNA computer[J]. Science, 2002, 296(5567): 499–502. doi: 10.1126/science.1069528 ZIMMERMANN K H. Efficient DNA sticker algorithms for NP-complete graph problems[J]. Computer Physics Communications, 2002, 144(3): 297–309. doi: 10.1016/S0010-4655(02)00270-9 XU Jin, QIANG Xiaoli, ZHANG Kai, et al. A DNA computing model for the graph vertex coloring problem based on a probe graph[J]. Engineering, 2018, 4(1): 61–77. doi: 10.1016/j.eng.2018.02.011 CHAVES-GONZÁLEZ J M and VEGA-RODRÍGUEZ M A. A multiobjective approach based on the behavior of fireflies to generate reliable DNA sequences for molecular computing[J]. Applied Mathematics and Computation, 2014, 227: 291–308. doi: 10.1016/j.amc.2013.11.032 PENG Ximei, ZHENG Xuedong, WANG Bin, et al. A micro-genetic algorithm for DNA encoding sequences design[C]. The 2nd International Conference on Control Science and Systems Engineering, Singapore, 2016: 10–14. YANG Gaijing, WANG Bin, ZHENG Xuedong, et al. IWO algorithm based on niche crowding for DNA sequence design[J]. Interdisciplinary Sciences: Computational Life Sciences, 2017, 9(3): 341–349. doi: 10.1007/s12539-016-0160-0 WANG Yanfeng, SHEN Yongpeng, ZHANG Xuncai, et al. An improved non-dominated sorting genetic algorithm-Ⅱ (INSGA-Ⅱ) applied to the design of DNA codewords[J]. Mathematics and Computers in Simulation, 2018, 151: 131–139. doi: 10.1016/j.matcom.2018.03.011 CHAVES-GONZÁLEZ J M and MARTÍNEZ-GIL J. An efficient design for a multi-objective evolutionary algorithm to generate DNA libraries suitable for computation[J]. Interdisciplinary Sciences: Computational Life Sciences, 2018, 11(3): 542–558. YANG Shuming, SHAO Dongguo, and LUO Yangjie. A novel evolution strategy for multiobjective optimization problem[J]. Applied Mathematics and Computation, 2005, 170(2): 850–873. doi: 10.1016/j.amc.2004.12.025 ARNOLD D V and BEYER H G. Investigation of the (μ, λ)-ES in the presence of noise[C]. The 2001 Congress on Evolutionary Computation, Seoul, South Korea, 2001, 1: 332–339. EBENAU C, ROTTSCHÄFER J, and THIERAUF G. An advanced evolutionary strategy with an adaptive penalty function for mixed-discrete structural optimisation[J]. Advances in Engineering Software, 2005, 36(1): 29–38. doi: 10.1016/j.advengsoft.2003.10.008 MEZURA-MONTES E and COELLO C A C. A simple multimembered evolution strategy to solve constrained optimization problems[J]. IEEE Transactions on Evolutionary Computation, 2005, 9(1): 1–17. doi: 10.1109/TEVC.2004.836819 XIAO J, XU Jin, CHEN Zhihua, et al. A hybrid quantum chaotic swarm evolutionary algorithm for DNA encoding[J]. Computers & Mathematics with Applications, 2009, 57(11/12): 1949–1958. CHAVES-GONZÁLEZ J M, VEGA-RODRÍGUEZ M A, and GRANADO-CRIADO J M. A multiobjective swarm intelligence approach based on artificial bee colony for reliable DNA sequence design[J]. Engineering Applications of Artificial Intelligence, 2013, 26(9): 2045–2057. doi: 10.1016/j.engappai.2013.04.011 MUHAMMAD M S, SELVAN K V, MASRA S M W, et al. An improved binary particle swarm optimization algorithm for DNA encoding enhancement[C]. 2011 IEEE Symposium on Swarm Intelligence, Paris, France, 2011: 1–8. CHAVES-GONZÁLEZ J M and VEGA-RODRÍGUEZ M A. DNA strand generation for DNA computing by using a multi-objective differential evolution algorithm[J]. Biosystems, 2014, 116: 49–64. doi: 10.1016/j.biosystems.2013.12.005 BUI L T and ALAM S. Multi-Objective Optimization in Computational Intelligence: Theory and Practice[M]. Hershey: IGI Global, 2008. SHIN S Y, LEE I H, KIM D, et al. Multiobjective evolutionary optimization of DNA sequences for reliable DNA computing[J]. IEEE Transactions on Evolutionary Computation, 2005, 9(2): 143–158. doi: 10.1109/TEVC.2005.844166 -





 下载:
下载:


 下载:
下载:
