基于多通道忆阻脉冲耦合神经网络的多帧图像超分辨率重建算法

董哲康; 杜晨杰; 林辉品; 赖俊昇; 胡小方; 段书凯

doi:10.11999/JEIT190868

基于多通道忆阻脉冲耦合神经网络的多帧图像超分辨率重建算法

doi: 10.11999/JEIT190868

董哲康^{1, 2},
杜晨杰¹,
林辉品^{1, 2, ,},
赖俊昇³,
胡小方⁴,
段书凯⁴

1.
杭州电子科技大学电子信息学院杭州 310018
2.
浙江大学电气工程学院杭州 310027
3.
牛津大学工程科学系英国牛津 OX1 3PJ
4.
西南大学人工智能学院重庆 400715

基金项目: 国家自然科学基金(61571394, 61601376)，浙江省属高校基本科研业务费项目(GK199900299012-010)

详细信息

作者简介:
董哲康：男，1989年生，副教授，主要研究方向为忆阻理论、基于忆阻器的神经形态系统研究

杜晨杰：男，1990年生，博士生，研究方向为忆阻理论、基于忆阻器的神经形态系统研究

林辉品：男，1987年生，讲师，主要研究方向为忆阻理论、基于忆阻器的神经形态系统研究

赖俊昇：男，1991年生，助理教授，主要研究方向为忆阻理论、基于忆阻器的神经形态系统研究

胡小方：女，1984年生，副教授，主要研究方向为忆阻器理论、基于忆阻器的非线性系统研究

段书凯：男，1973年生，教授，主要研究方向为忆阻器理论、微纳系统研究

通讯作者:
林辉品　linhuipin@hdu.edu.cn

中图分类号: TN601; TN911.73
计量
- 文章访问数: 6061
- HTML全文浏览量: 1831
- PDF下载量: 168
- 被引次数: 0
出版历程
- 收稿日期: 2019-11-01
- 修回日期: 2020-01-12
- 网络出版日期: 2020-02-12
- 刊出日期: 2020-06-04

Multi-channel Memristive Pulse Coupled Neural Network Based Multi-frame Images Super-resolution Reconstruction Algorithm

1.
School of Electronic Information, Hangzhou Dianzi University, Hangzhou 310018, China
2.
College of Electrical Engineering, Zhejiang University, Hangzhou 310027, China
3.
Department of Engineering Science, University of Oxford, Oxford OX1 3PJ, United Kingdom
4.
College of Artificial Intelligence, Southwest University, Chongqing 400715, China

Funds: The National Natural Science Foundation of China (61571394, 61601376), The Fundamental Research Funds for the Provincial Universities (GK199900299012-010)

摘要

摘要: 高清晰度的图像是信息获取和精确分析的前提，研究多帧图像的超分辨率重建能够有效解决因外部拍摄环境引起的图像细节丢失、边缘模糊等问题。该文基于纳米级忆阻器，设计一种多通道忆阻脉冲耦合神经网络模型(MMPCNN)，能够有效模拟网络中连接系数的动态变化，解决神经网络中固有的参数估计问题。同时，将提出的网络应用于多帧图像超分辨率重建中，实现低分辨率配准图像的融合操作，并通过基于稀疏编码的单帧图像超分辨率重构算法对获得的初始高分辨率图像进行优化。最终，一系列计算机仿真及分析(主观/客观分析)验证了该文提出方案的正确性和有效性。
- 忆阻器 /
- 脉冲耦合神经网络 /
- 多帧图像 /
- 超分辨率重建
Abstract: The high-resolution image is the prerequisite of information acquisition and precise analysis. Multi-frame super-resolution images reconstruction technologies are able to address many image degraded issues (caused by external shooting environment), such as detail information lost, blurred edges, and so forth. According to the nanoscale memristor, a Multi-channel Memristive Pulse Coupled Neural Network (MMPCNN) model is proposed. This model is able to simulate the adaptive-variable linking coefficient in pulse coupled neural network. Meanwhile, the proposed network is applied to the multi-frame super resolution reconstruction for fusing the registered low resolution images. Furthermore, the sparse coding based super resolution method is performed to improve the original high-resolution image. Finally, a series of computer experiments and the relevant subjective/objective analysis jointly illustrate the validity and effectiveness of the entire scheme.
- Memristor /
- Pulse coupled neural network /
- Multi-frame images /
- Super-resolution reconstruction

HTML全文

图 1 VTEAM忆阻器仿真结果

下载: 全尺寸图片幻灯片

图 2 多通道忆阻脉冲耦合神经网络MMPCNN

下载: 全尺寸图片幻灯片

图 3 图像降质模型

下载: 全尺寸图片幻灯片

图 4 提出的图像超分辨率算法流程图

下载: 全尺寸图片幻灯片

图 5 多帧图像超分辨重构的实现流程

下载: 全尺寸图片幻灯片

图 6 对比实验仿真结果

下载: 全尺寸图片幻灯片

图 7 对比实验仿真结果

下载: 全尺寸图片幻灯片

参考文献(20)

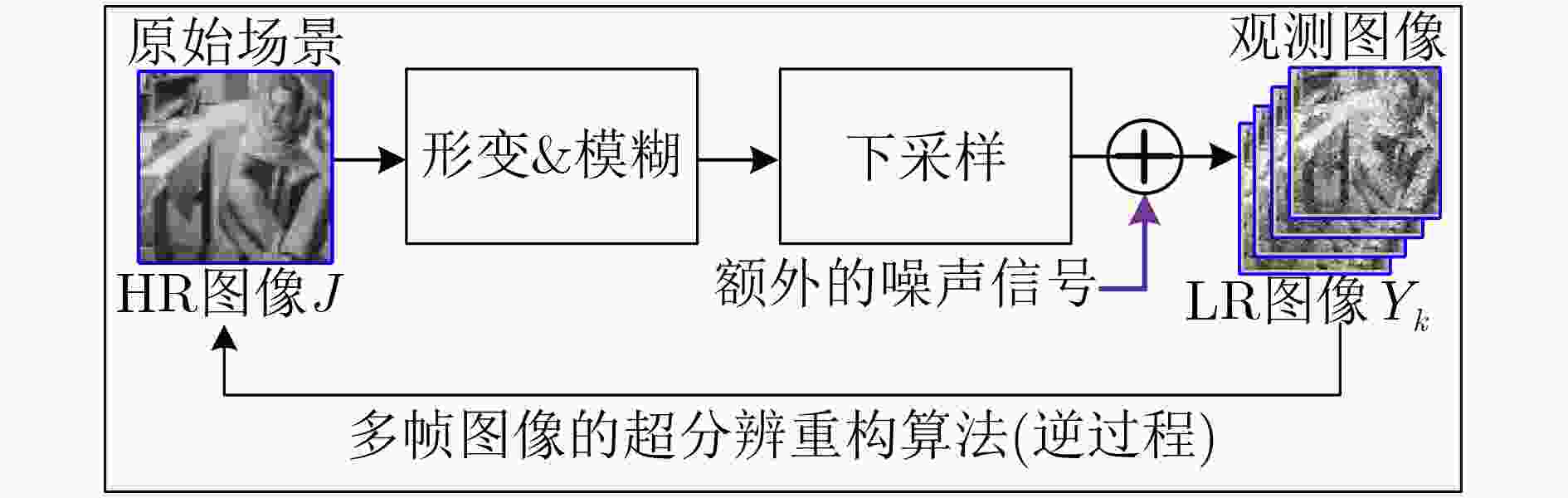
PARK S C, PARK M K, and KANG M G. Super-resolution image reconstruction: A technical overview[J]. IEEE Signal Processing Magazine, 2003, 20(3): 21–36. doi: 10.1109/MSP.2003.1203207

赵小强, 宋昭漾. 多级跳线连接的深度残差网络超分辨率重建[J]. 电子与信息学报, 2019, 41(10): 2501–2508. doi: 10.11999/JEIT190036

ZHAO Xiaoqiang and SONG Zhaoyang. Super-resolution reconstruction of deep residual network with multi-level skip connections[J]. Journal of Electronics &Information Technology, 2019, 41(10): 2501–2508. doi: 10.11999/JEIT190036

DONG Zhekang, LAI C S, XU Zhao, et al. Single image super-resolution via the implementation of the hardware-friendly sparse coding[C]. The 37th Chinese Control Conference, Wuhan, China, 2018: 8132–8137.

HUI Zheng, WANG Xiumei, and GAO Xinbo. Fast and accurate single image super-resolution via information distillation network[C]. 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, USA, 2018: 723–731.

BAKER S and KANADE T. Super-resolution optical flow[R]. Technical Report CMU-RI-TR-36, 1999.

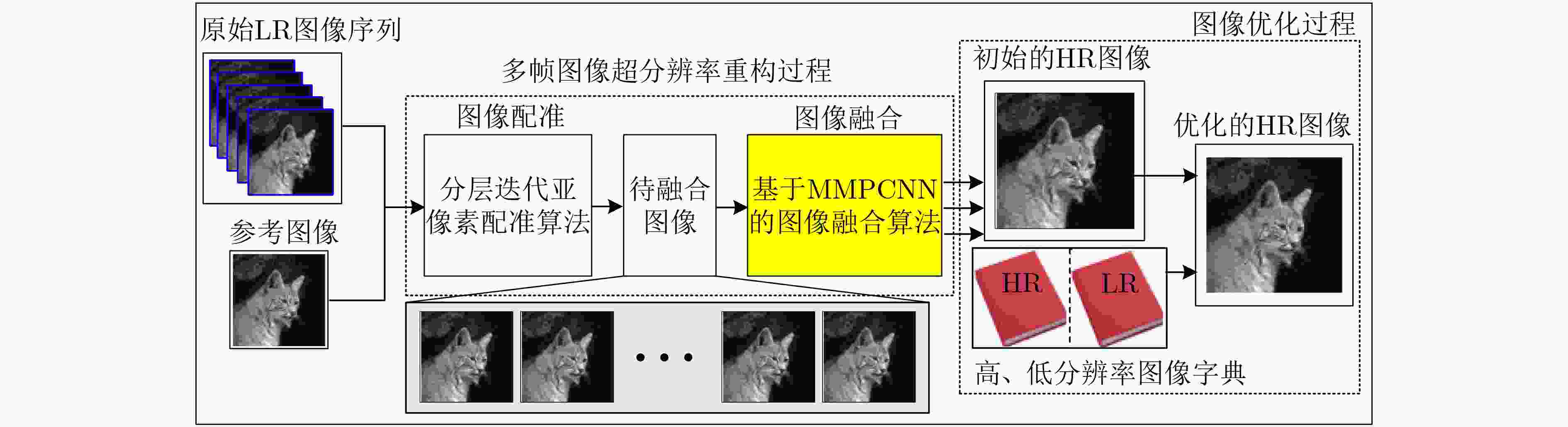
NING Beijia and GAO Xinbo. Multi-frame image super-resolution reconstruction using sparse co-occurrence prior and sub-pixel registration[J]. Neurocomputing, 2013, 117: 128–137. doi: 10.1016/j.neucom.2013.01.019

XU Jieping, LIANG Yonghui, LIU Jin, et al. Online multi-frame super-resolution of image sequences[J]. EURASIP Journal on Image and Video Processing, 2018(1): 136–10. doi: 10.1186/s13640-018-0376-5

AIZAWA K, KOMATSU T, SAITO T, et al. Subpixel registration for a high resolution imaging scheme using multiple imagers[C]. 1993 IEEE International Conference on Acoustics, Speech, and Signal Processing, Minneapolis, USA 1993: 133–136.

SINHA A and WU Xiaolin. Fast generalized motion estimation and superresolution[C]. 2007 IEEE International Conference on Image Processing, San Antonio, USA, 2007: V–413–V–416.

ARYA M S and JAIN P. Fifth-level Second-generation Wavelet-based Image Fusion Algorithm for Visual Quality Enhancement of Digital Image Data[M]. MISHRA D K, AZAR A T, and JOSHI A. Information and Communication Technology. Singapore: Springer, 2018: 139–149.

WU Zhiliang, HUANG Yongdong, and ZHANG Kang. Remote sensing image fusion method based on PCA and Curvelet transform[J]. Journal of the Indian Society of Remote Sensing, 2018, 46(5): 687–695. doi: 10.1007/s12524-017-0736-0

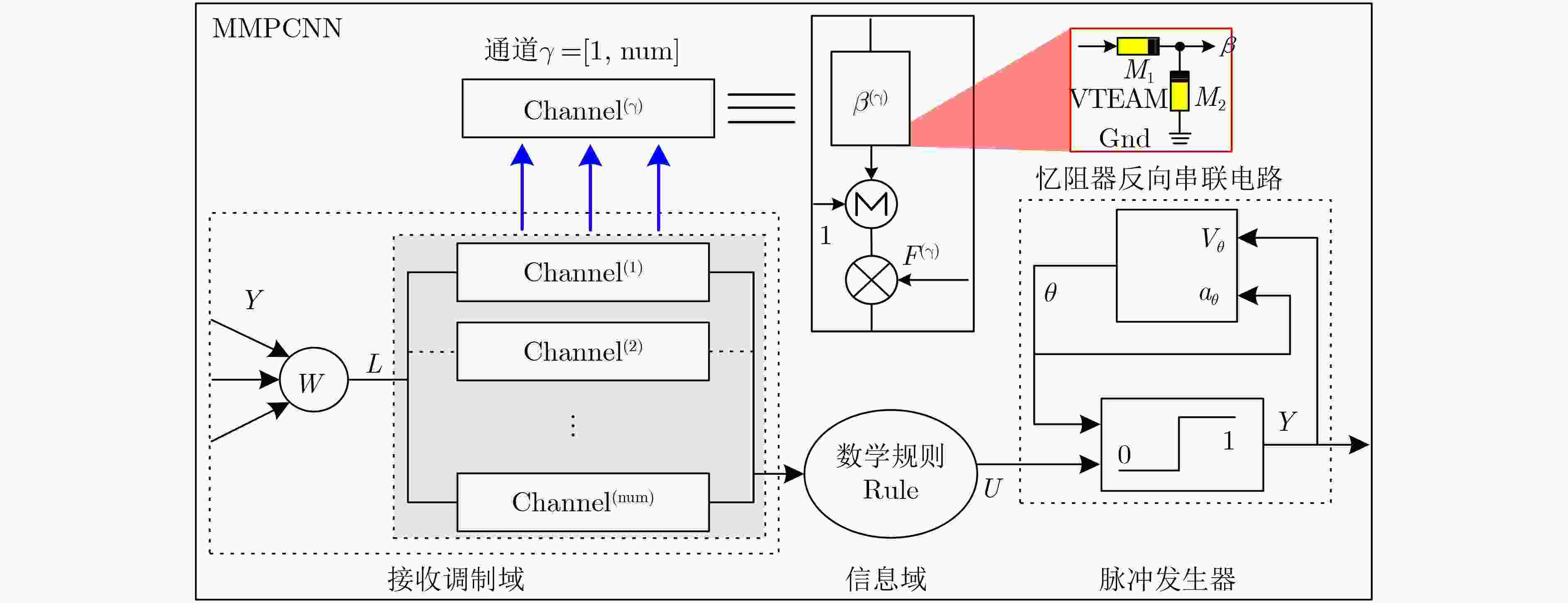
DONG Zhekang, LAI C S, QI Donglian, et al. A general memristor-based pulse coupled neural network with variable linking coefficient for multi-focus image fusion[J]. Neurocomputing, 2018, 308: 172–183. doi: 10.1016/j.neucom.2018.04.066

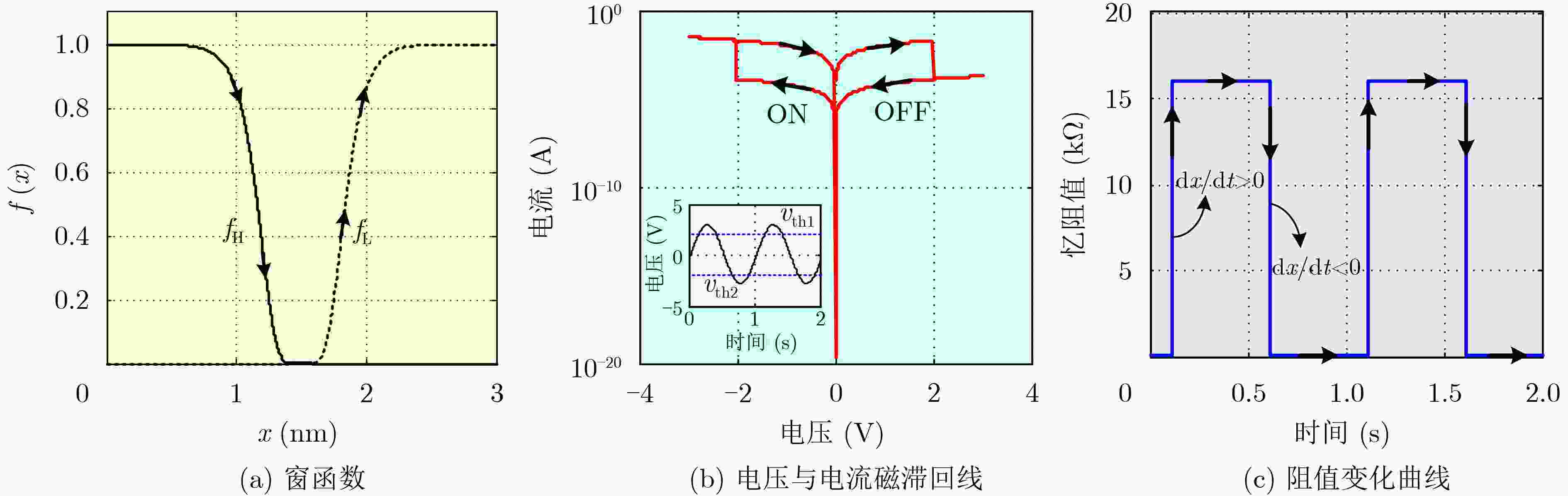
李志军, 向林波, 肖文润. 一种通用的记忆器件模拟器及在串联谐振电路中的应用[J]. 电子与信息学报, 2017, 39(7): 1626–1633. doi: 10.11999/JEIT161060

LI Zhijun, XIANG Linbo, and XIAO Wenrun. Universal mem-elements emulator and its application in RLC circuit[J]. Journal of Electronics &Information Technology, 2017, 39(7): 1626–1633. doi: 10.11999/JEIT161060

KVATINSKY S, RAMADAN M, FRIEDMAN E G, et al. VTEAM: A general model for voltage-controlled memristors[J]. IEEE Transactions on Circuits and Systems II: Express Briefs, 2015, 62(8): 786–790. doi: 10.1109/TCSII.2015.2433536

KUPFER B, NETANYAHU N S, and SHIMSHONI I. An efficient SIFT-based mode-seeking algorithm for sub-pixel registration of remotely sensed images[J]. IEEE Geoscience and Remote Sensing Letters, 2015, 12(2): 379–383. doi: 10.1109/LGRS.2014.2343471

QU Xiaobo, HU Changwei, and YAN Jingwen. Image fusion algorithm based on orientation information motivated pulse coupled neural networks[C]. The 7th World Congress on Intelligent Control and Automation, Chongqing, China, 2008: 2437–2441.

CHENG Xuan, ZENG Ming, and LIU Xinguo. Feature-preserving filtering with L₀ gradient minimization[J]. Computers & Graphics, 2014, 38: 150–157.

TIMOFTE R, DE V, and VAN GOOL L. Anchored neighborhood regression for fast example-based super-resolution[C]. 2013 IEEE International Conference on Computer Vision, Sydney, Austrlia, 2013: 1920–1927.

DONG Chao, LOY C C, HE Kaiming, et al. Learning a deep convolutional network for image super-resolution[C]. The 13th European Conference on Computer Vision, Zurich, Switzerland, 2014: 184–199.

https://github.com/tingfengainiaini/sparseCodingSuperResolution, 2019.

施引文献

资源附件(0)

访问统计