A Simple Inductor-free Memristive Chaotic Circuit and Its Characteristics
-
摘要: 采用非理想有源电压控制忆阻器和磁通控制型光滑3次非线性忆阻器,该文设计了一种不含电感的简单(只含5个电子元器件)双忆阻混沌电路。采用常规的非线性分析手段详细研究了电路参数变化时系统的基本动力学行为,例如平衡点稳定性分析,相轨图以及李雅普诺夫指数谱和分岔图等。通过调节系统控制参数,该系统可产生多涡卷、多翼以及暂态混沌等十分丰富的动力学现象。此外,还研究了系统依赖于忆阻器初始状态的多稳态,得到了一些有意义的结果。为验证电路的可行性及稳定性,通过对忆阻器的模拟等效电路的搭建,并将该等效电路应用于所提出的混沌电路中,硬件电路实验结果以及Multisim电路仿真结果与理论分析一致。Abstract: A simple two-memristor chaotic circuit without inductance (only five electronic components) is designed by using a non-ideal active voltage control memristor and a flux-controlled smooth cubic nonlinear memristor. When the circuit parameters change, the basic dynamic behaviors of the system are studied in detail by the means of conventional nonlinear analysis, such as the analysis of equilibrium stability, phase diagram, Lyapunov exponent spectrum and bifurcation diagram. With the parameters changing, the proposed system can produce various phenomena of dynamics such as multi-scrolls, multi-wings and transient transition behaviors. Furthermore, the multistability characteristics of the system are also studied in the condition of changing the initial state of two memristors in system respectively, and some meaningful results are obtained. In order to verify the feasibility and stability of the circuit, the analog equivalent circuit of each memristor is constructed, and it is applied to the proposed chaotic circuit. The experimental results of the hardware circuit and the circuit simulation results of the Multisim are in good agreement with the theoretical analysis.
-
Key words:
- Memristor /
- Chaotic circuit /
- Multistability /
- Transient transition behaviors
-
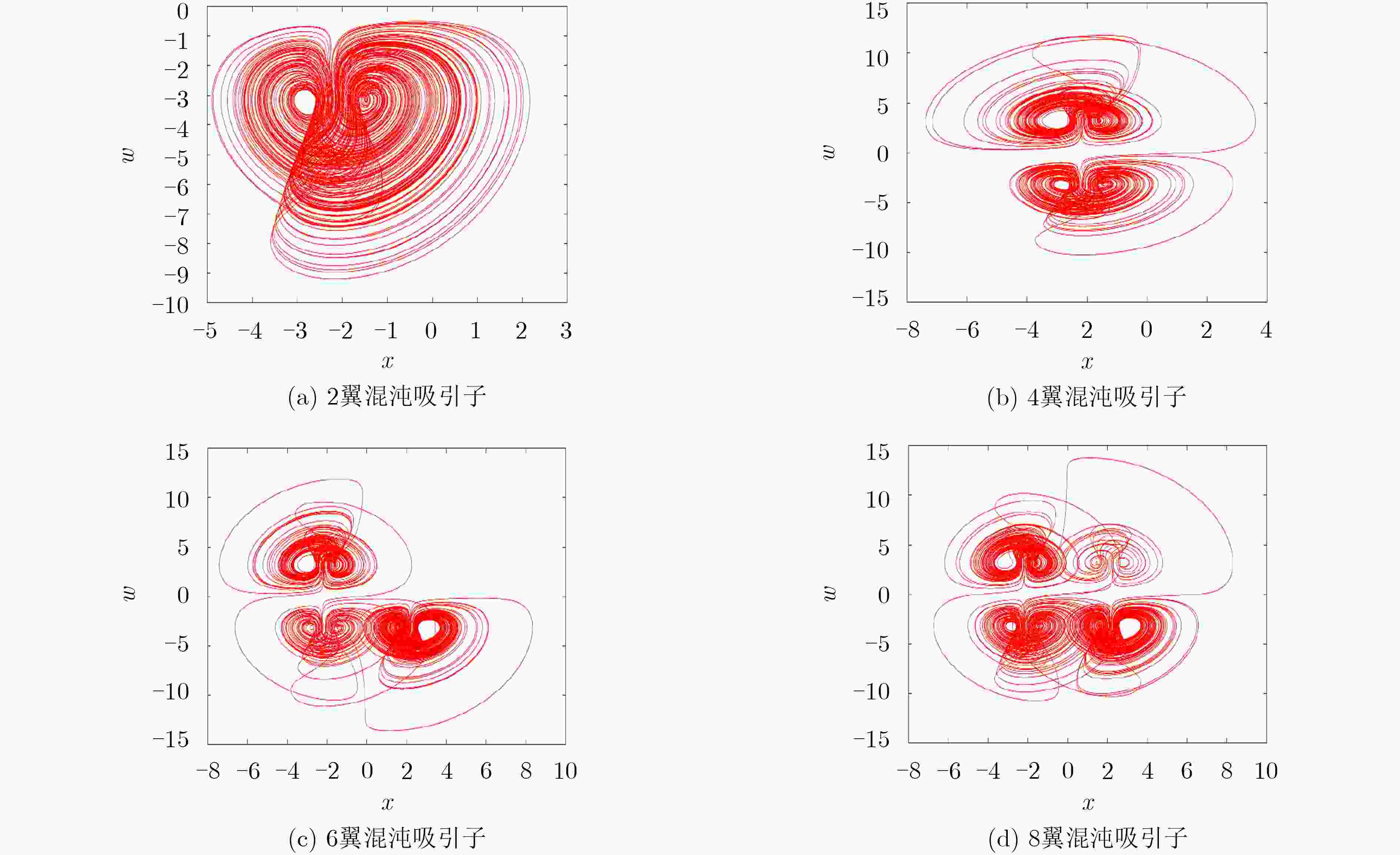
表 1 忆阻器W3随初始状态变化所产生的多稳态举例
z(0)取值 LE李雅普诺夫指数 系统状态 4.0 (+, 0, –, –) 2翼混沌吸引子 6.5 (+, 0, –, –) 4翼混沌吸引子 13.5 (+, 0, –, –) 6翼混沌吸引子 17.5 (+, 0, –, –) 8翼混沌吸引子 表 2 简洁无电感忆阻混沌电路的参数取值
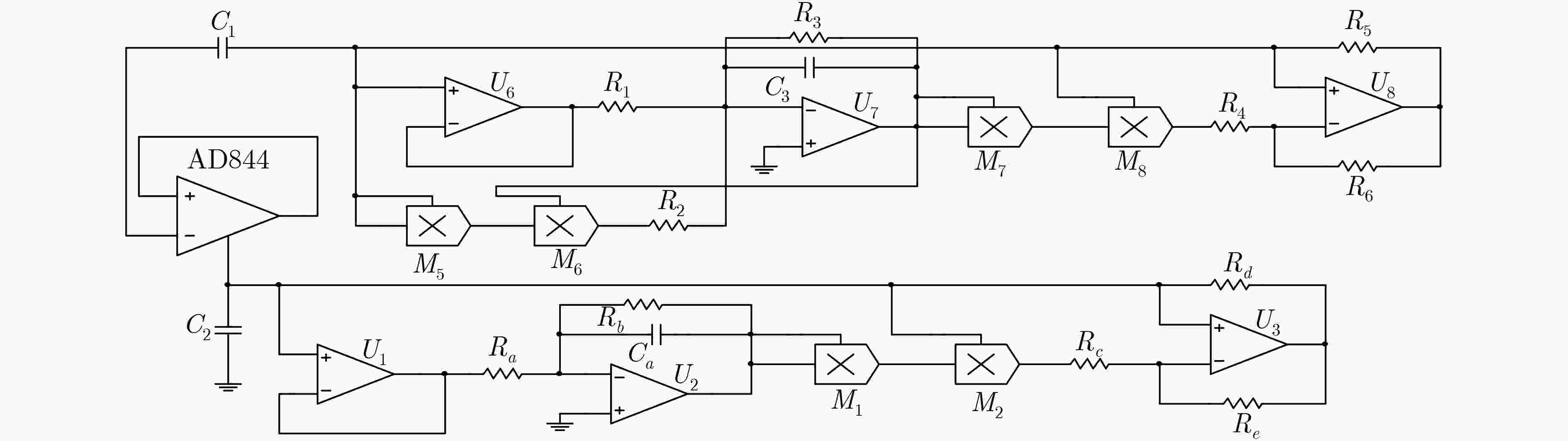
参数 名称 参值 $ {C_a},{C_1},{C_3}$ 电容 1 nF C2 电容 25 nF $ {g_a},{\rm{ }}{g_b},{\rm{ }}{g_{3,}}{g_4}$ 增益 1 $ {g_1},{\rm{ }}{g_2}$ 增益 0.1 R1 电阻 0.25 kΩ R2 电阻 50.00 kΩ R3 电阻 25.00 kΩ $ {R_4},{\rm{ }}{R_c}$ 电阻 10.00 kΩ Rb 电阻 16.70 kΩ $ {R_d},{R_e}_,{R_5}{,}{R_6}$ 电阻 2.00 kΩ -
郑利京, 王光义, 张娜. 基于忆阻器的混合CMOS乘法器设计[J]. 杭州电子科技大学学报: 自然科学版, 2019, 39(2): 1–5. doi: 10.13954/j.cnki.hdu.2019.02.001ZHENG Lijing, WANG Guangyi, and ZHANG Na. A multiplier design based on hybrid memristor-CMOS[J]. Journal of Hangzhou Dianzi University:Natural Sciences, 2019, 39(2): 1–5. doi: 10.13954/j.cnki.hdu.2019.02.001 WANG Xingyuan and ZHANG Huili. A novel image encryption algorithm based on genetic recombination and hyper-chaotic systems[J]. Nonlinear Dynamics, 2016, 83(1/2): 333–346. doi: 10.1007/s11071-015-2330-8 DUAN Shukai, HU Xiaofang, DONG Zhekang, et al. Memristor-based cellular nonlinear/neural network: Design, analysis, and applications[J]. IEEE Transactions on Neural Networks and Learning Systems, 2015, 26(6): 1202–1213. doi: 10.1109/TNNLS.2014.2334701 刘军, 段书凯, 李天舒, 等. 机械臂的自旋忆阻RBF神经网络控制系统设计[J]. 仪器仪表学报, 2018, 39(8): 212–219. doi: 10.19650/j.cnki.cjsi.J1803068LIU Jun, DUAN Shukai, LI Tianshu, et al. Design of RBF neural network control system based on spintronic memristor for robotic manipulator[J]. Chinese Journal of Scientific Instrument, 2018, 39(8): 212–219. doi: 10.19650/j.cnki.cjsi.J1803068 WANG Chunni, LÜ Mi, ALSAEDI A, et al. Synchronization stability and pattern selection in a memristive neuronal network[J]. Chaos, 2017, 27(11): 113108. doi: 10.1063/1.5004234 吴杰, 王光义, 丘嵘, 等. 忆阻器数字化仿真器的设计与实现[J]. 杭州电子科技大学学报: 自然科学版, 2018, 38(5): 1–6. doi: 10.13954/j.cnki.hdu.2018.05.001WU Jie, WANG Guangyi, QIU Rong, et al. Design and implementation of digital simulator for memristor[J]. Journal of Hangzhou Dianzi University:Natural Sciences, 2018, 38(5): 1–6. doi: 10.13954/j.cnki.hdu.2018.05.001 WU Xiangjun, FU Zhengye, and KURTHS J. A secure communication scheme based generalized function projective synchronization of a new 5D hyperchaotic system[J]. Physica Scripta, 2015, 90(4): 045210. doi: 10.1088/0031-8949/90/4/045210 ALJAFAR M J, PERKOWSKI M A, ACKEN J M, et al. A time-efficient CMOS-memristive programmable circuit realizing logic functions in generalized AND-XOR structures[J]. IEEE Transactions on Very Large Scale Integration (VLSI) Systems, 2018, 26(1): 23–36. doi: 10.1109/TVLSI.2017.2750074 阮静雅, 孙克辉, 牟俊. 基于忆阻器反馈的Lorenz超混沌系统及其电路实现[J]. 物理学报, 2016, 65(19): 190502. doi: 10.7498/aps.65.190502RUAN Jingya, SUN Kehui, and MOU Jun. Memristor-based Lorenz hyper-chaotic system and its circuit implementation[J]. Acta Physica Sinica, 2016, 65(19): 190502. doi: 10.7498/aps.65.190502 BAO Bocheng, JIANG Tao, XU Quan, et al. Coexisting infinitely many attractors in active band-pass filter-based memristive circuit[J]. Nonlinear Dynamics, 2016, 86(3): 1711–1723. doi: 10.1007/s11071-016-2988-6 RUAN Jingya, SUN Kehui, MOU Jun, et al. Fractional-order simplest memristor-based chaotic circuit with new derivative[J]. The European Physical Journal Plus, 2018, 133(1): No. 3, 1–12. doi: 10.1140/epjp/i2018-11828-0 MUTHUSWAMY B and CHUA L O. Simplest chaotic circuit[J]. International Journal of Bifurcation and Chaos, 2010, 20(5): 1567–1580. doi: 10.1142/S0218127410027076 MUTHUSWAMY B. Implementing memristor based chaotic circuits[J]. International Journal of Bifurcation and Chaos, 2010, 20(5): 1335–1350. doi: 10.1142/S0218127410026514 ITOH M and CHUA L O. Memristor oscillators[J]. International Journal of Bifurcation and Chaos, 2008, 18(11): 3183–3206. doi: 10.1142/S0218127408022354 YUAN Fang and LI Yuxia. A chaotic circuit constructed by a memristor, a memcapacitor and a meminductor[J]. An Interdisciplinary Journal of Nonlinear Science, 2019, 29(10): 101101. doi: 10.1063/1.5125673 LI Chuang, MIN Fuhong, and LI Chunbiao. Multiple coexisting attractors of the serial-parallel memristor-based chaotic system and its adaptive generalized synchronization[J]. Nonlinear Dynamics, 2018, 94(4): 2785–2806. doi: 10.1007/s11071-018-4524-3 RAJAGOPAL K, LI Chunbiao, NAZARIMEHR F, et al. Chaotic dynamics of modified Wien bridge oscillator with fractional order memristor[J]. Radioengineering, 2019, 28(1): 165–174. 洪庆辉, 曾以成, 李志军. 含磁控和荷控两种忆阻器的混沌电路设计与仿真[J]. 物理学报, 2013, 63(23): 230502. doi: 10.7498/aps.62.230502HONG Qinghui, ZENG Yicheng, and LI Zhijun. Design and simulation of chaotic circuit for flux-controlled memristor and charge-controlled memristor[J]. Acta Physica Sinica, 2013, 63(23): 230502. doi: 10.7498/aps.62.230502 BAO Bocheng, ZHANG Xi, BAO Han, et al. Dynamical effects of memristive load on peak current mode buck-boost switching converter[J]. Chaos, Solitons & Fractals, 2019, 122: 69–79. CHEN Chengjie, CHEN Jingqi, BAO Han, et al. Coexisting multi-stable patterns in memristor synapse-coupled Hopfield neural network with two neurons[J]. Nonlinear Dynamics, 2019, 95(4): 3385–3399. doi: 10.1007/s11071-019-04762-8 BAO Bocheng, MA Zhenghua, XU Jianping, et al. A simple memristor chaotic circuit with complex dynamics[J]. International Journal of Bifurcation and Chaos, 2011, 21(9): 2629–2645. doi: 10.1142/S0218127411029999 WANG Chunhua, LIU Xiaoming, and XIA Hu. Multi-piecewise quadratic nonlinearity memristor and its 2N-scroll and 2N+1-scroll chaotic attractors system[J]. An Interdisciplinary Journal of Nonlinear Science, 2017, 27(3): 033114. doi: 10.1063/1.4979039 谭志平, 曾以成, 李志军, 等. 浮地型忆阻器混沌电路的分析与实现[J]. 仪器仪表学报, 2014, 35(9): 2123–2129.TAN Zhiping, ZENG Yicheng, and LI Zhijun. Analysis and implementation of a floating memristor chaotic circuit[J]. Chinese Journal of Scientific Instrument, 2014, 35(9): 2123–2129. BAO Bocheng, JIANG Tao, WANG Guangyi, et al. Two-memristor-based Chua’s hyperchaotic circuit with plane equilibrium and its extreme multistability[J]. Nonlinear Dynamics, 2017, 89(2): 1157–1171. doi: 10.1007/s11071-017-3507-0 CHEN Mo, SUN Mengxia, BAO Bocheng, et al. Controlling extreme multistability of memristor emulator-based dynamical circuit in flux-charge domain[J]. Nonlinear Dynamics, 2018, 91(2): 1395–1412. doi: 10.1007/s11071-017-3952-9 TAN Qiwei, ZENG Yicheng, and LI Zhijun. A simple inductor-free memristive circuit with three line equilibria[J]. Nonlinear Dynamics, 2018, 94(3): 1585–1602. doi: 10.1007/s11071-018-4443-3 -





 下载:
下载:

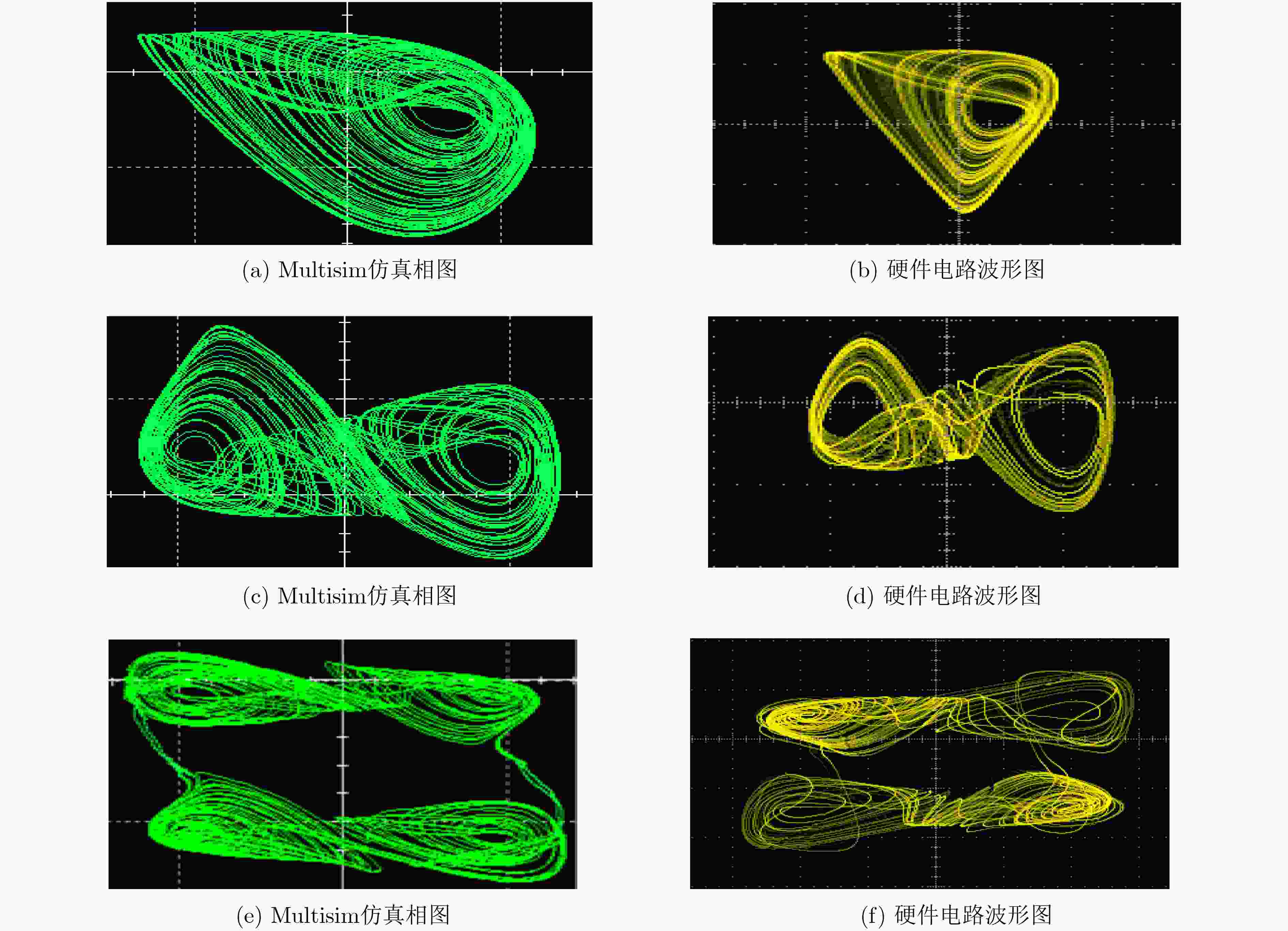


 下载:
下载:
