Image Encryption Algorithm of Based on Variable Step Length Josephus Traversing and DNA Dynamic Coding
-
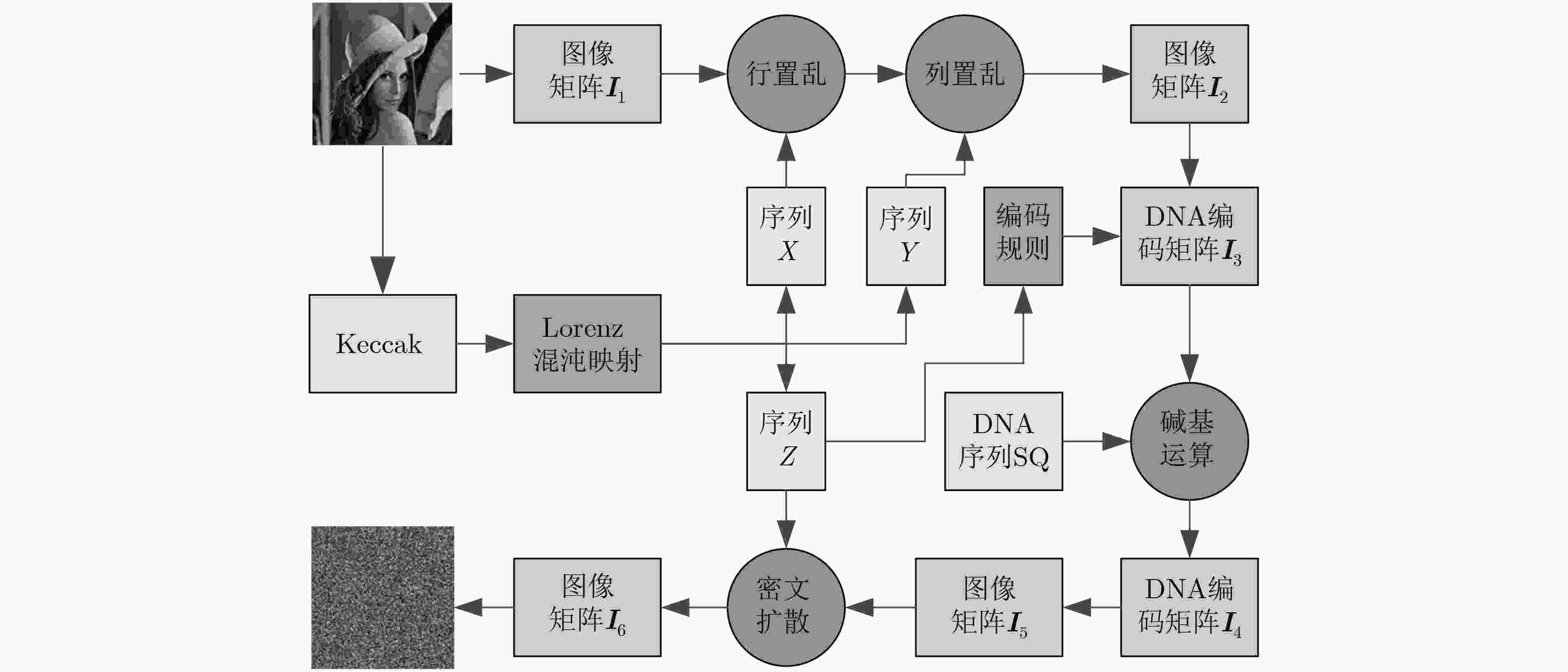
摘要: 数字图像传输和存储的安全问题已成为信息安全研究的热点。该文提出一种基于变步长约瑟夫遍历和DNA动态编码的图像加密方法。首先将混沌映射产生的随机序列作为约瑟夫遍历的变步长，改进约瑟夫遍历问题，并采用改进的约瑟夫遍历对图像像素位置进行置乱；其次，动态选择DNA编码规则，对图像像素进行DNA编码，并与给定的DNA序列进行碱基运算；DNA编码规则的动态选择，很好地解决了DNA编码规则少所带来的安全隐患，提高了算法的安全性。最后通过密文反馈和混沌系统迭代来进一步增强算法的混淆和扩散特性。实验和安全性分析结果表明，该算法不仅对密钥的敏感性强，而且能有效抵御统计性分析和穷举分析等攻击操作。Abstract: The security of digital image transmission and storage has become a hotspot of information security research. An image encryption algorithm based on variable step length Josephus traversing and DNA dynamic coding is proposed. Firstly, through the thorough analysis of Joseph traversing, the random sequence generated by chaotic map is taken as the variable step length of Joseph traversing, and the pixel position is permutated. Secondly, according to the random sequence generated by chaotic map, the DNA coding rules of pixel points transformation are selected, and the image is dynamically encoded into DNA strand, and the DNA sequence is calculated based on the principle of complementary base pairing. Because the DNA coding rules of the pixels transformation are dynamic, the hidden danger caused by the lack of DNA coding rules is well solved, and the security of the algorithm is improved. Finally, the permutation and diffusion characteristics of the algorithm are further enhanced by ciphertext feedback and chaotic system iteration. Experiment and security analysis results show that the algorithm not only has large key space and strong sensitivity to keys, but also can effectively resist attacks such as statistical analysis and brutal analysis.
-
Key words:
- Image encryption /
- Dynamic DNA encoding /
- Josephus traversing /
- Displace
-
表 5 加密密钥敏感性(%)
初始值 NPCR UACI $ {x}'_{0} $+10–10 99.5956 33.5652 $ {y}'_{0} $+10–10 99.6109 33.3368 $ {z}'_{0} $+10–10 99.6261 33.5378 
下载: 导出CSV
表 6 密钥的解密敏感性分析(%)
初始值 NPCR UACI $ {x}'_{0} $+10–10 99.6048 34.6094 $ {y}'_{0} $+10–10 99.5956 34.4388 $ {x}'_{0} $+10–10 99.5529 34.5867
下载: 导出CSV
表 7 原始图像发生微小改变时NPCR和UACI的值(%)
图像 NPCR UACI Lena 99.5378 33.3080 Cameraman 99.6209 33.5080 Brain 99.5375 33.6244 White 99.6284 33.8780
下载: 导出CSV
表 8 直方图的χ2分布统计
原始图像χ2分布 密文图像χ2分布 检测结果 Lena 39851.3281 239.0847 通过 Cameraman 161271.875 212.0456 通过 Brain 1044635.67 258.3025 通过
下载: 导出CSV
表 9 原始图像和密文图像各方向的相关系数
图像 相关系数 原始图像 密文图像 水平
方向垂直
方向对角线
方向水平
方向垂直
方向对角线
方向Cameraman 0.9540 0.9087 0.8813 –0.0070 0.0083 0.0013 Brain 0.9965 0.9959 0.9942 –0.0038 0.0051 0.0042
下载: 导出CSV
表 10 原始图像和密文图像的信息熵
图像 信息熵 原始图像 密文图像 Lena 6.8794 7.9873 Cameraman 6.9046 7.9976 Brain 5.0329 7.9970 White 0 7.9970
下载: 导出CSV
表 11 Cameraman图像遭受数据丢失攻击后解密图像的各项指标
裁剪面积 相关性 NPCR UACI 水平 垂直 对角线 原图 0.9501 0.9231 0.9011 0 0 1/64 0.9145 0.8689 0.8649 1.7548 0.6277 1/16 0.8075 0.7754 0.7442 6.6223 2.3429 1/4 0.4667 0.4507 0.4352 25.7019 9.0683
下载: 导出CSV
-
BEHNIA S, AKHSHANI A, MAHMODI H, et al. A novel algorithm for image encryption based on mixture of chaotic maps[J]. Chaos, Solitons & Fractals, 2008, 35(2): 408–419. doi: 10.1016/j.chaos.2006.05.011 SHANNON C E. Communication theory of secrecy systems[J]. The Bell System Technical Journal, 1949, 28(4): 656–715. doi: 10.1002/j.1538-7305.1949.tb00928.x ÖZKAYNAK F. Brief review on application of nonlinear dynamics in image encryption[J]. Nonlinear Dynamics, 2018, 92(2): 305–313. doi: 10.1007/s11071-018-4056-x CHEN G R, MAO Y B, and CHUI C K. A symmetric image encryption scheme based on 3D chaotic cat maps[J]. Chaos, Solitons & Fractals, 2004, 21(3): 749–761. doi: 10.1016/j.chaos.2003.12.022 WANG Xinyuan, WANG Xiaojuan, ZHAO Jianfeng, et al. Chaotic encryption algorithm based on alternant of stream cipher and block cipher[J]. Nonlinear Dynamics, 2011, 63(4): 587–597. doi: 10.1007/s11071-010-9821-4 LEIER A, RICHTER C, BANZHAF W, et al. Cryptography with DNA binary strands[J]. Biosystems, 2000, 57(1): 13–22. doi: 10.1016/S0303-2647(00)00083-6 SHIMANOVSKY B, FENG J, and POTKONJAK M. Hiding Data in DNA[M]. PETITCOLAS F A P. Information Hiding. Berlin: Springer, 2008: 373–386. doi: 10.1007/3-540-36415-3_24. BONEH D, DUNWORTH C, and LIPTON R J. Breaking DES Using a Molecular Computer[M]. LIPTON R J and BAUM E B. DNA Based Computers I. Providence: American Mathematical Society, 1996: 37–65. GEHANI A, LABEAN T, and REIF J. DNA-based Cryptography[M]. JONOSKA N, PĂUN G, and ROZENBERG G. Aspects of Molecular Computing. Berlin: Springer, 2003: 233–249. doi: 10.1007/978-3-540-24635-0_12. CLELLAND C T, RISCA V, BANCROFT C. Hiding messages in DNA microdots[J]. Nature, 1999, 399(6736): 533–534. doi: 10.1038/21092 LE GOFF G C, BLUM L J, and MARQUETTE C A. Shrinking Hydrogel-DNA spots generates 3D microdots arrays[J]. Macromolecular Bioscience, 2013, 13(2): 227–233. doi: 10.1002/mabi.201200370 WANG Yanfeng, HAN Qinqin, CUI Guangzhao, et al. Hiding messages based on DNA sequence and recombinant DNA technique[J]. IEEE Transactions on Nanotechnology, 2019, 18: 299–307. doi: 10.1109/TNANO.2019.2904842 ZHANG Yinan, WANG Fei, CHAO Jie, et al. DNA origami cryptography for secure communication[J]. Nature Communications, 2019, 10: 5469. doi: 10.1038/s41467-019-13517-3 NAMASUDRA S, DEVI D, KADRY S, et al. Towards DNA based data security in the cloud computing environment[J]. Computer Communications, 2020, 151: 539–547. doi: 10.1016/j.comcom.2019.12.041 ZHANG Xuncai, ZHOU Zheng, and NIU Ying. An image encryption method based on the feistel network and dynamic DNA encoding[J]. IEEE Photonics Journal, 2018: 3901014. doi: 10.1109/JPHOT.2018.2859257 WANG Xingyuan, ZHANG Yingqian, and ZHAO Yuanyuan. A novel image encryption scheme based on 2-D logistic map and DNA sequence operations[J]. Nonlinear Dynamics, 2015, 82(3): 1269–1280. doi: 10.1007/s11071-015-2234-7 CHAI Xiuli, CHEN Yiran, and BROYDE Lucie. A novel chaos-based image encryption algorithm using DNA sequence operations[J]. Optics and Lasers in Engineering, 2017, 88: 197–213. doi: 10.1016/j.optlaseng.2016.08.009 WANG Xingyuan, ZHU Xiaoqiang, and ZHANG Yingqian. An image encryption algorithm based on Josephus traversing and mixed chaotic map[J]. IEEE Access, 2018, 6: 23733–23746. doi: 10.1109/ACCESS.2018.2805847 郭毅, 邵利平, 杨璐. 基于约瑟夫和Henon映射的比特位图像加密算法[J]. 计算机应用研究, 2015, 32(4): 1131–1137. doi: 10.3969/j.issn.1001-3695.2015.04.041GUO Yi, SHAO Liping, and YANG Lu. Bit-level image encryption algorithm based on Josephus and Henon chaotic map[J]. Application Research of Computers, 2015, 32(4): 1131–1137. doi: 10.3969/j.issn.1001-3695.2015.04.041 梁静, 李红菊, 赵凤, 等. 一种构造GC常重量DNA码的方法[J]. 电子与信息学报, 2019, 41(10): 2423–2427. doi: 10.11999/JEIT190070LIANG Jing, LI Hongju, ZHAO Feng, et al. A method for constructing GC constant weight DNA codes[J]. Journal of Electronics &Information Technology, 2019, 41(10): 2423–2427. doi: 10.11999/JEIT190070 CHAI Zongqian, LIANG Shili, HU Guorong, et al. Periodic characteristics of the Josephus ring and its application in image scrambling[J]. EURASIP Journal on Wireless Communications and Networking, 2018, 2018(1): 162. doi: 10.1186/s13638-018-1167-5 -
下载:
图(5) / 表(12)
计量
- 文章访问数: 3254
- HTML全文浏览量: 875
- PDF下载量: 166
- 被引次数: 0
