NAND Gate Computational Model Based on the DNA Origami Template
-
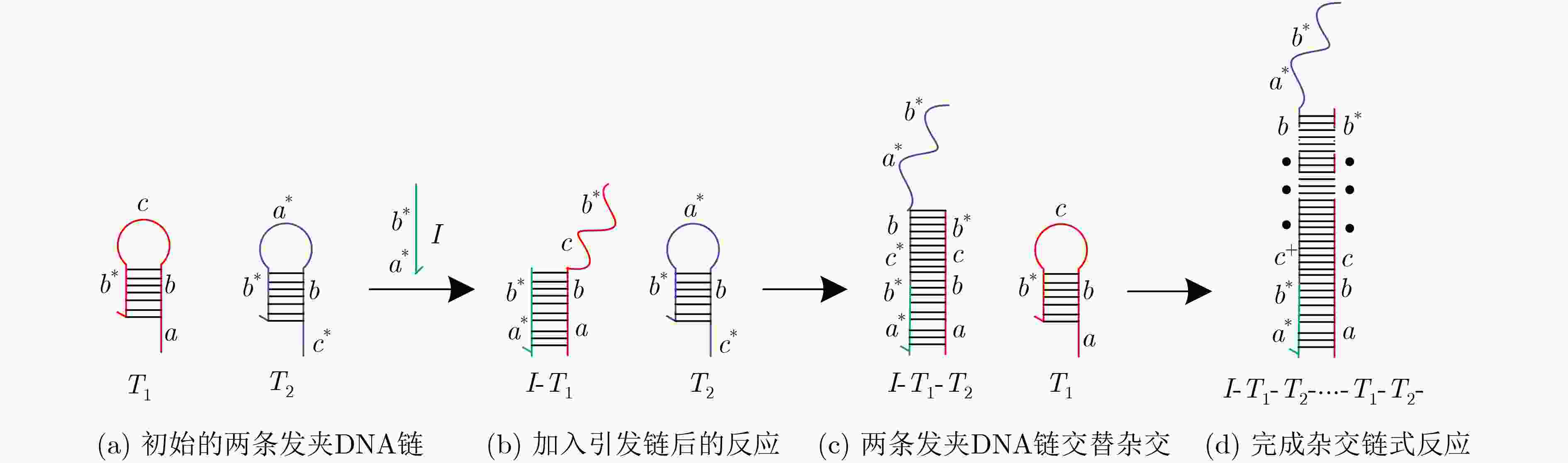
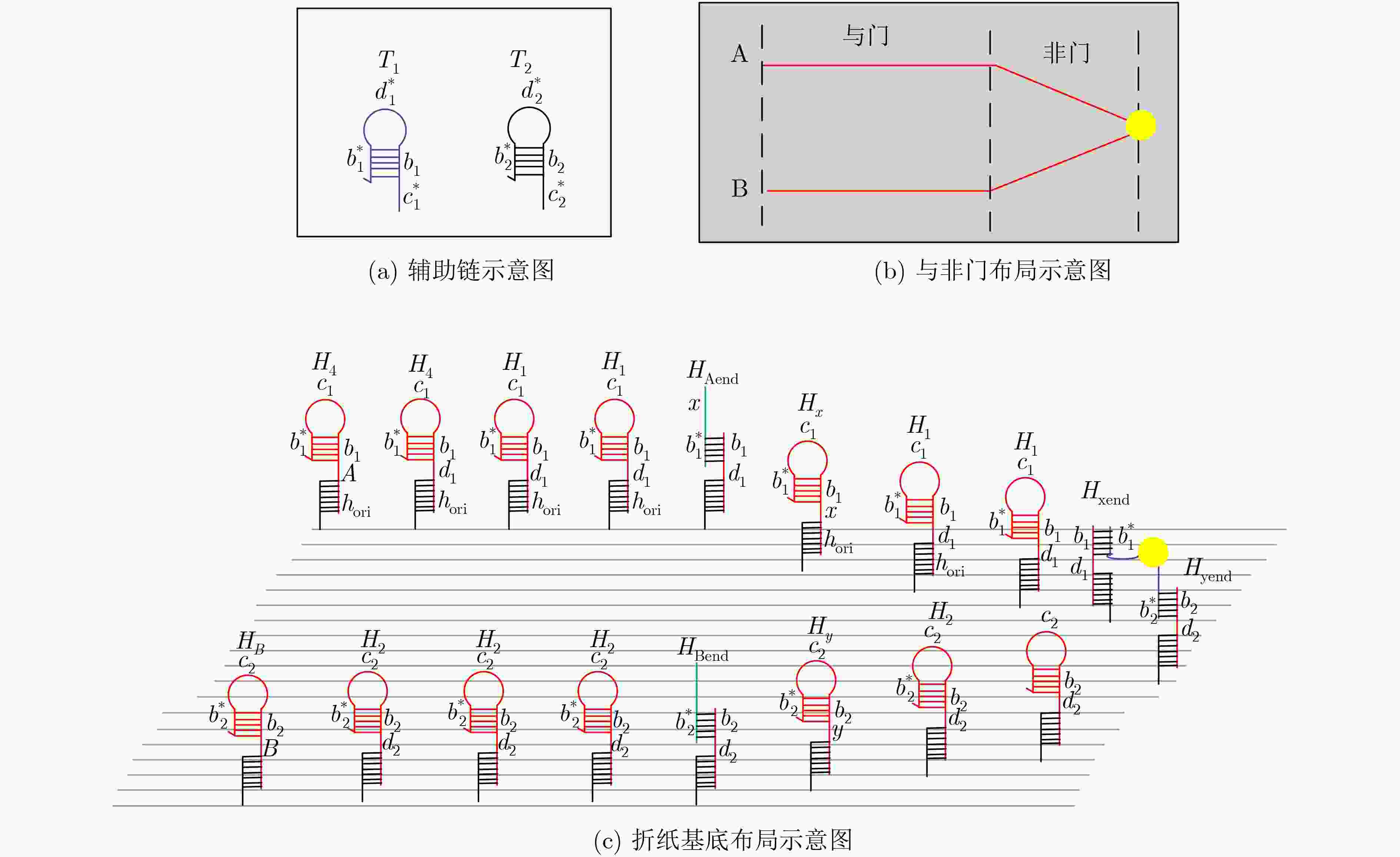
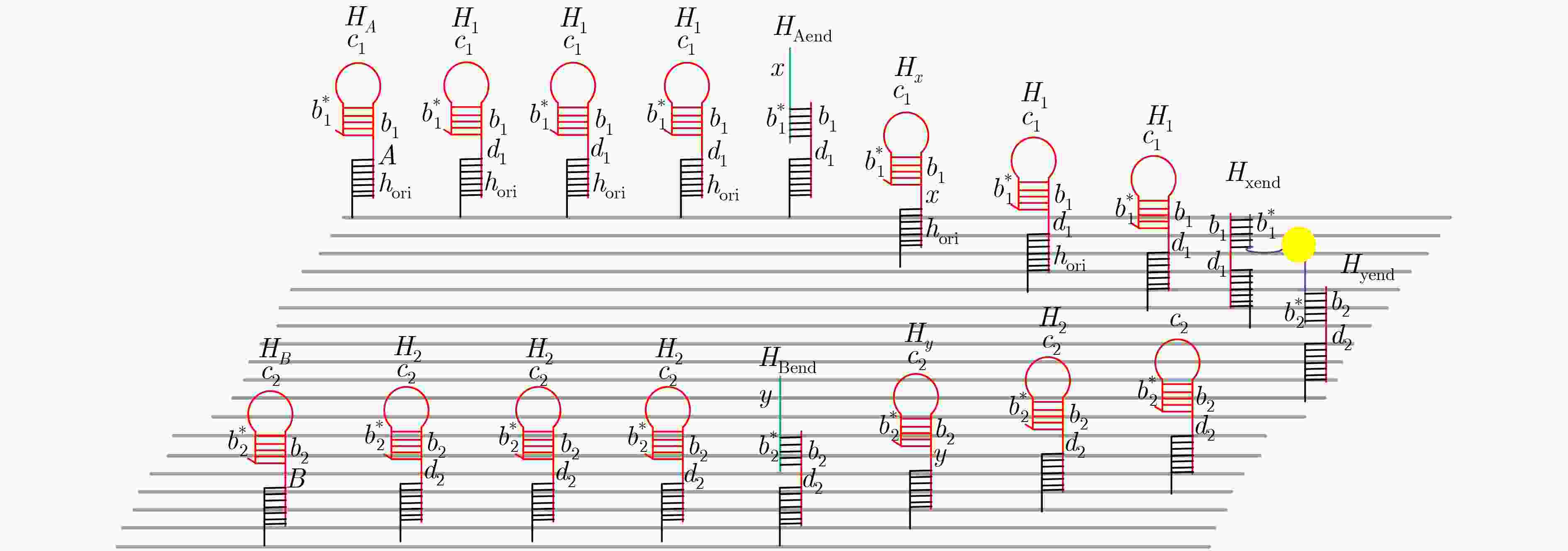
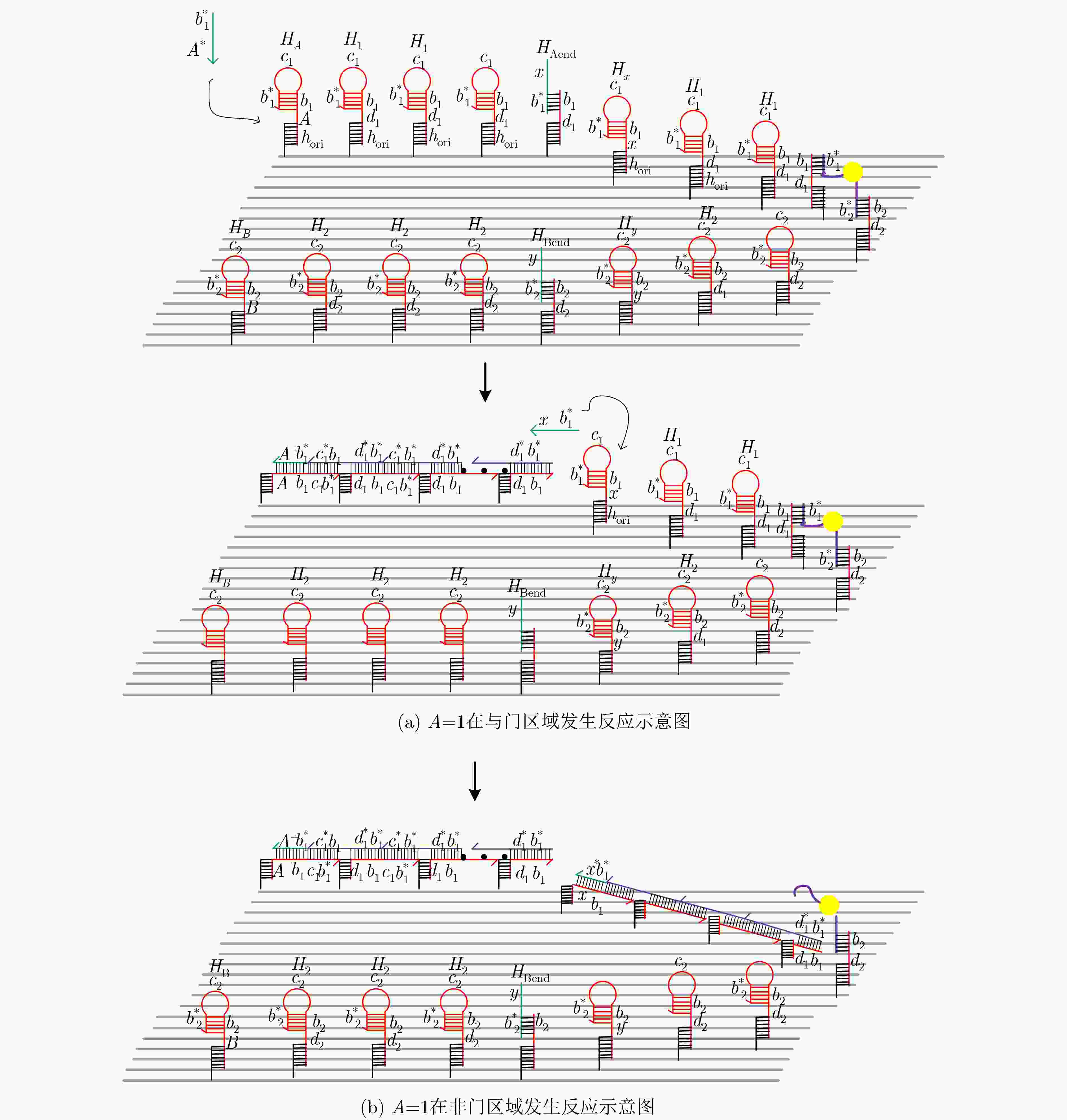
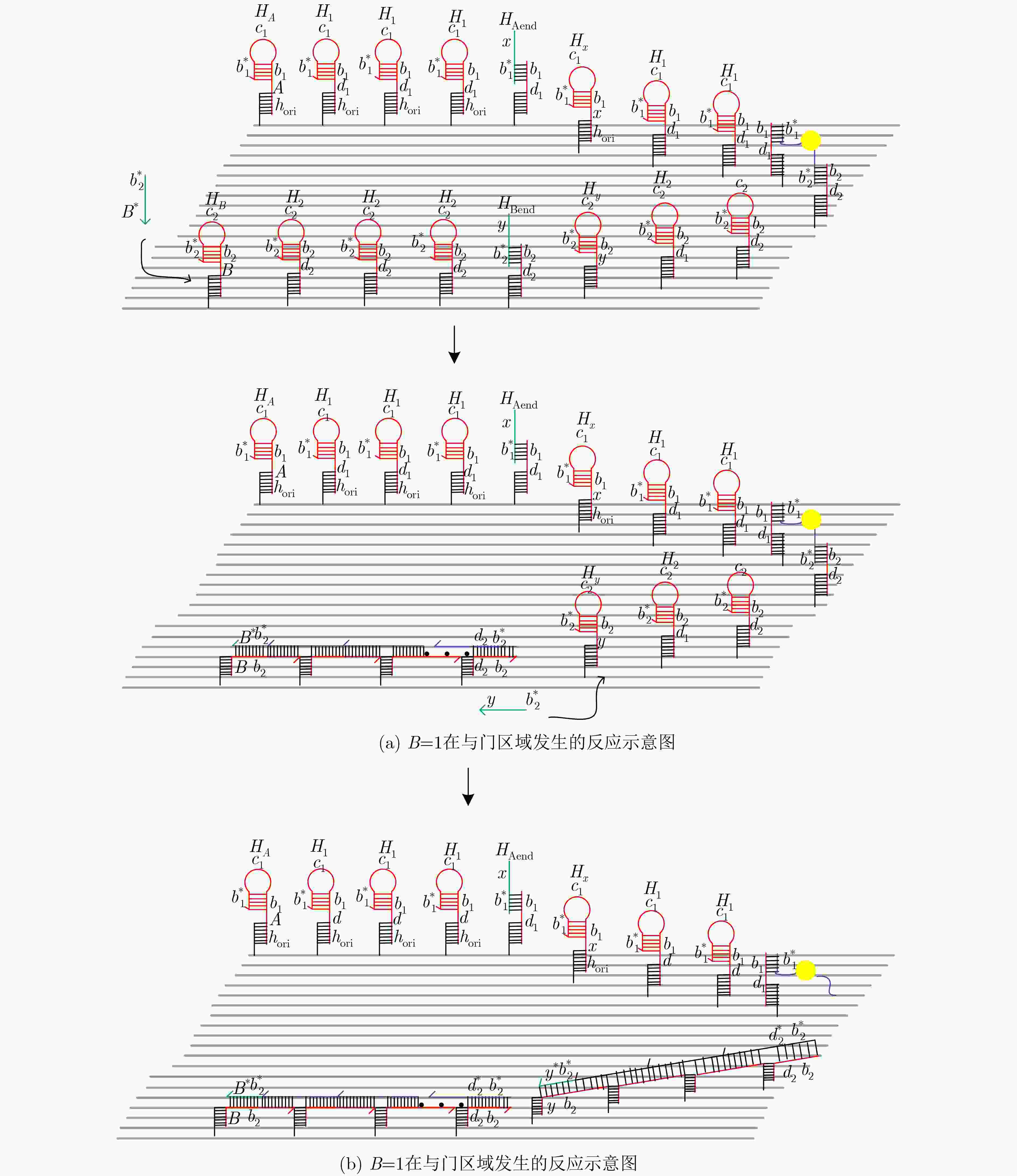
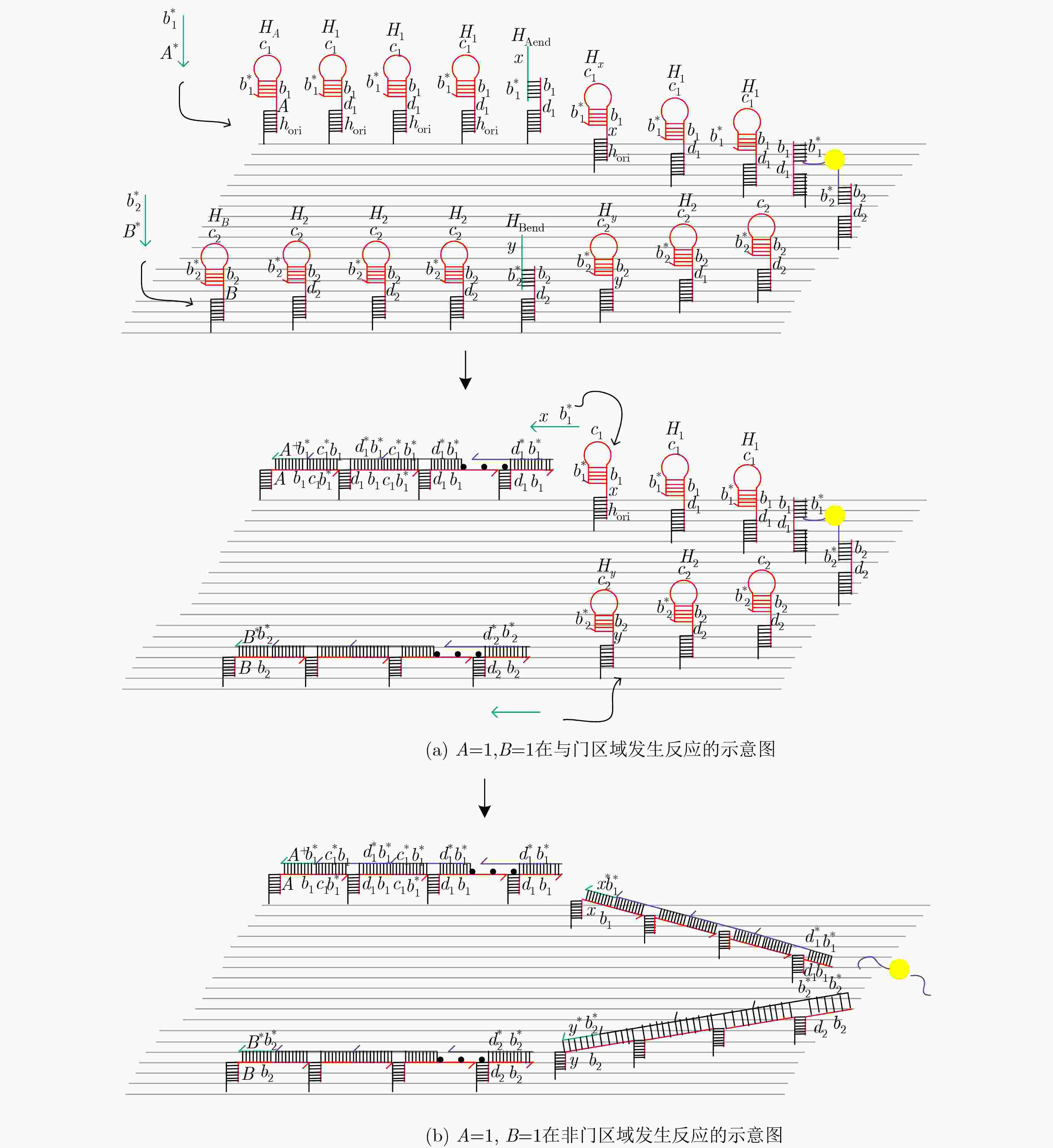
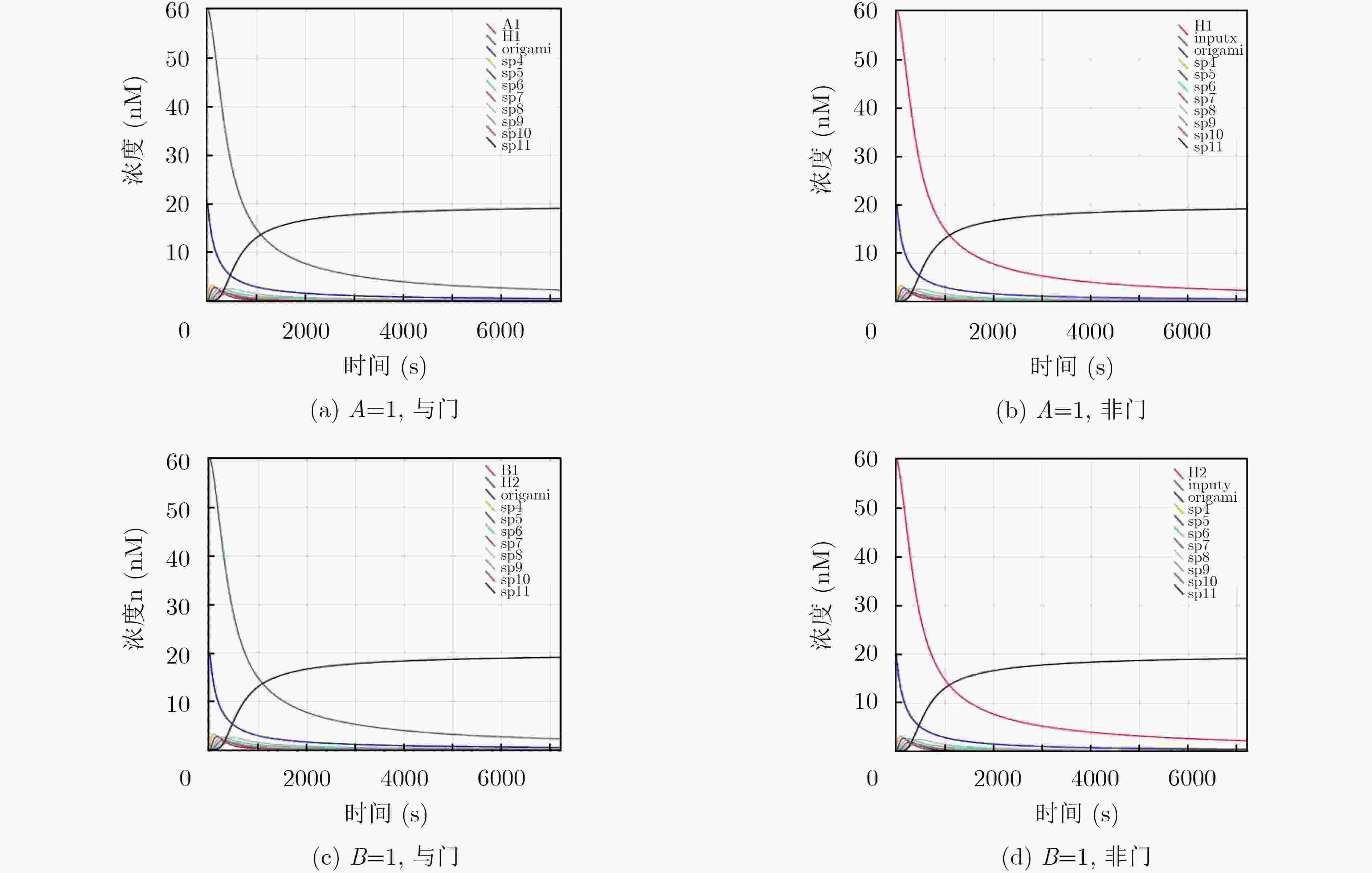
摘要: 与非门(NAND)的本质是与门(AND)和非门(NOT)的叠加,先进行与运算,再进行非运算,它是建立DNA计算机的基础。为了实现与非门的计算,该文在DNA折纸基底上建立了一个与非门计算模型,逻辑值的输入是通过在DNA折纸基底上发生有向的杂交链式反应(HCR)来完成的,输入链先经过与门区域再经过非门区域,最后通过DNA折纸基底上是否还保留纳米金颗粒来显示计算结果的真假。利用Visual DSD对该计算模型进行仿真模拟,显示该计算模型具有较好的可行性。Abstract: The essence of NAND gate is the superposition of AND gate and NOT gate. The AND gate operation is performed first, and then the NOT gate is performed. It is the basis of the DNA computer. In order to realize the computing of NAND gate, a NAND gate computational model is established based on the DNA origami template. The inputs of the logic value are completed by the Hybridization Chain Reaction (HCR) on the DNA origami template. The input strands first react with the AND gate region and then react with the NOT gate region. The result of the reaction is shown by dynamically separation of the gold nanoparticles on the DNA origami template. The simulation of the model through Visual DSD shows that the system has the advantages of high feasibility.
-
Key words:
- DNA computing /
- DNA origami /
- NAND gate
-
表 1 与非门真值表
A 0 0 1 1 B 0 1 0 1 F 1 1 1 0 -
ADLEMAN L M. Molecular computation of solutions to combinatorial problems[J]. Science, 1994, 266(5187): 1021–1024. doi: 10.1126/science.7973651 LIPTON R J. DNA solution of hard computational problems[J]. Science, 1995, 268(5210): 542–545. doi: 10.1126/science.7725098 SAKAMOTO K, GOUZU H, KOMIYA K, et al. Molecular computation by DNA hairpin formation[J]. Science, 2000, 288(5469): 1223–1226. doi: 10.1126/science.288.5469.1223 YIN Zhixiang, CUI Jianzhong, YANG Jing, et al. DNA computing model of the integer linear programming problem based on molecular beacon[C]. International Conference on Intelligent Computing, Kunming, China, 2006: 238–247. GUO Ping and LIU Lili. A surface-based DNA algorithm for the 0–1 programming problem[C]. The 3rd International Conference on Innovative Computing Information and Control, Dalian, China, 2008. QIAN Lulu and WINFREE E. Scaling up digital circuit computation with DNA strand displacement cascades[J]. Science, 2011, 32(6034): 1196–1201. YANG Jing, ZHANG Cheng, LIU Shi, et al. A molecular computing model for 0-1 programming problem using DNA nanoparticles[J]. Journal of Computational and Theoretical Nanoscience, 2013, 10(10): 2380–2384. doi: 10.1166/jctn.2013.3218 LI Fei, LIU Jingming, and LI Zheng. DNA computation based on self-assembled nanoparticle probes for 0-1 integer programming problem[J]. Mathematics and Computers in Simulation, 2018, 151: 140–146. doi: 10.1016/j.matcom.2017.02.004 YIN Zhixiang, CUI Jianzhong, and YANG Jing. Integer programming problem based on plasmid DNA computing model[J]. Chinese Journal of Electronics, 2017, 26(6): 1284–1288. doi: 10.1049/cje.2017.07.013 XU Jin, QIANG Xiaoli, ZHANG Kai, et al. A DNA computing model for the graph vertex coloring problem based on a probe graph[J]. Engineering, 2018, 4(1): 61–77. doi: 10.1016/j.eng.2018.02.011 YURKE B, TURBERFIELD A J, MILLS JR A P, et al. A DNA-fuelled molecular machine made of DNA[J]. Nature, 2000, 406(6796): 605–608. doi: 10.1038/35020524 DIRKS R M and PIERCE N A. Triggered amplification by hybridization chain reaction[J]. Proceedings of the National Academy of Sciences of the United States of America, 2004, 101(43): 15275–15278. doi: 10.1073/pnas.0407024101 ROTHEMUND P W K. Folding DNA to create nanoscale shapes and patterns[J]. Nature, 2006, 440(7082): 297–302. doi: 10.1038/nature04586 LAKIN M R, PARKER D, CARDELLI L, et al. Design and analysis of DNA strand displacement devices using probabilistic model checking[J]. Journal of the Royal Society Interface, 2012, 9(72): 1470–1485. doi: 10.1098/rsif.2011.0800 CONDON A, KIRKPATRICK B, and MAŇUCH J. Reachability bounds for chemical reaction networks and strand displacement systems[J]. Natural Computing, 2014, 13(4): 499–516. doi: 10.1007/s11047-013-9403-8 MARDIAN R, SEKIYAMA K, and FUKUDA T. DNA strand displacement for stochastic decision making based on immune’s clonal selection algorithm[J]. Information Technologies Knowledge, 2013, 7(1): 34–45. YANG Jing, DONG Chen, DONG Yafei, et al. Logic nanoparticle beacon triggered by the binding-induced effect of multiple inputs[J]. ACS Applied Materials & Interfaces, 2014, 6(16): 14486–14492. YANG Jing, JIANG Shuoxing, LIU Xiangrong, et al. Aptamer-binding directed DNA origami pattern for logic gates[J]. ACS Applied Materials & Interfaces, 2016, 8(49): 34054–34060. PAN Linqiang, WANG Zhiyu, LI Yifan, et al. Nicking enzyme-controlled toehold regulation for DNA logic circuits[J]. Nanoscale, 2017, 9(46): 18223–18228. doi: 10.1039/C7NR06484E YANG Jing, WU Ranfeng, LI Yifan, et al. Entropy-driven DNA logic circuits regulated by DNAzyme[J]. Nucleic Acids Research, 2018, 46(16): 8532–8541. doi: 10.1093/nar/gky663 XU Fei, WU Tingfang, SHI Xiaolong, et al. A study on a special DNA nanotube assembled from two single-stranded tiles[J]. Nanotechnology, 2019, 30(11): 115602. doi: 10.1088/1361-6528/aaf9bc PAN Linqiang, HU Yingxin, DING Taoli, et al. Aptamer-based regulation of transcription circuits[J]. Chemical Communications, 2019, 55(51): 7378–7381. doi: 10.1039/C9CC03141C WANG Xiaolong, BAO Zhenmin, HU Jingjie, et al. Solving the SAT problem using a DNA computing algorithm based on ligase chain reaction[J]. Biosystems, 2008, 91(1): 117–125. doi: 10.1016/j.biosystems.2007.08.006 俞洋, 苏邵, 晁洁. 基于“DNA折纸术”设计哈密顿路径问题的解决方案[J]. 中国科学: 化学, 2015, 45(11): 1226–1230. doi: 10.1360/N032015-00035YU Yang, SU Shao, and CHAO Jie. A "DNA origami"-based approach to the solution of Hamilton path problem[J]. Scientia Sinica Chimica, 2015, 45(11): 1226–1230. doi: 10.1360/N032015-00035 俞洋, 苏邵, 晁洁. 基于“DNA折纸术”设计图着色问题的解决方案[J]. 南京大学学报: 自然科学, 2016, 52(4): 656–661.YU Yang, SU Shao, and CHAO Jie. A "DNA origami"-based approach to the solution of graph coloring problem[J]. Journal of Nanjing University:Natural Sciences, 2016, 52(4): 656–661. YANG Jing, SONG Zhichao, LIU Shi, et al. Dynamically arranging gold nanoparticles on DNA origami for molecular logic gates[J]. ACS Applied Materials & Interfaces, 2016, 8(34): 22451–22456. ZHANG Qiang, WANG Xiaobiao, Wang Xiaojun, et al. Solving probability reasoning based on DNA strand displacement and probability modules[J]. Computational Biology and Chemistry, 2017, 71: 274–279. doi: 10.1016/j.compbiolchem.2017.09.011 CHAO Jie, WANG Jianbang, WANG Fei, et al. Solving mazes with single-molecule DNA navigators[J]. Nature Materials, 2019, 18(3): 273–279. doi: 10.1038/s41563-018-0205-3 TANG Zhen, YIN Zhixiang, SUN Xia, et al. Dynamically NAND gate system on DNA origami template[J]. Computers in Biology and Medicine, 2019, 109: 112–120. doi: 10.1016/j.compbiomed.2019.04.026 -





 下载:
下载:
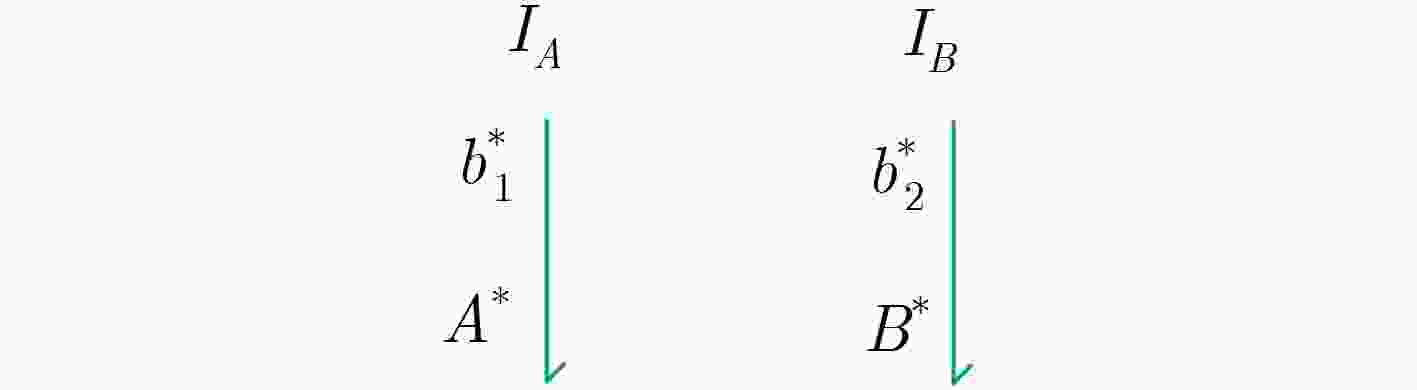



 下载:
下载:
