Verifiable Attribute-based Keyword Search Scheme with Privacy Preservation
-
摘要:
针对传统基于属性关键字搜索(ABKS)方案存在访问结构泄密、用户侧计算量高及缺乏完整性验证问题,该文提出具有隐私保护和完整性可验证的基于属性的关键字搜索方案。该方案提出了有序多值属性访问结构和有序多值属性集,固定每个属性的位置,减少参数及相关计算,提高了方案的效率,而在密钥生成时计算具体属性取值的哈希值,从而达到区别多值属性取值的不同。同时,采用Hash和对运算实现对访问结构的隐藏,防止访问结构泄密;采用倒序索引结构和Merkle树建立数据认证树,可验证云服务器返回文档和外包解密结果的正确性。此外,支持外包解密以降低用户侧的计算量。安全分析和实验表明所提方案实现云中共享数据的可验证性、关键字不可区分性和关键字不可链接性,且是高效的。
Abstract:To address the problems of the leakage of access structure, high computation of user side and lack of integrity verification in current Attribute-Based Keyword Search (ABKS) scheme, a verifiable attribute-based keyword search scheme with privacy preservation is proposed. The scheme adopts the ordered multi-valued attribute access structure and ordered multi-valued attribute set, and fixes the position of each attribute to reduce the parameters and related computation cost and to improve the efficiency of the scheme, while in key generation, the Hash values of specific attributes are calculated to distinguish the different values of multi-valued attributes. At the same time, Hash and pair operation are used to hide the access structure and prevent the disclosure of the access structure. The inverted index structure and Merkle tree are used to establish the data authentication tree, which can verify the correctness of the document returned by the cloud server provider and the result of outsourced decryption. In addition, outsourced decryption is used to reduce the computation cost on the user side. Finally, formal proofs and experimental results show that the scheme achieve verifiability of shared data in the cloud, keyword undistinguishable and keyword unlinkable, and is efficient.
-
表 1 属性值
${\rm{att}}{{\rm{r}}_{\rm{1}}}$ ${\rm{att}}{{\rm{r}}_{\rm{2}}}$ $ ··· $ ${\rm{att}}{{\rm{r}}_n}$ ${V_1}$ ${V_2}$ $ ··· $ ${V_n}$ $1$ $2$ $ ··· $ $n$ $n + 1$ $n + 2$ $ ··· $ $2n$ $2n+1$ $2n+2$ $ ··· $ $3n$ $ ··· $ $ ··· $ $ ··· $ $ ··· $ 表 3 通信开销比较
文献[13] 文献[19] 本文方案 密钥生成 $(2n + 3)\left| {{G_2}} \right|+\left| {{Z_p}} \right|$ $(n + 5)\left| {{G_2}} \right|+n\left| {{Z_p}} \right|$ $(n + 3)\left| {{G_1}} \right|+\left| {{Z_p}} \right|$ 门限生成 $(2n + 3)\left| {{G_2}} \right|$ $\left| {{G_2}} \right|+\left| {{G_1}} \right|$ $3\left| {{G_1}} \right| + \left| {{Z_p}} \right|$ 搜索 $(3n + 1)\left| {{G_1}} \right|$ $3\left| {{G_2}} \right| + n\left| {{G_1}} \right|$ $\left| {{G_2}} \right| + \left| {{G_1}} \right|$ 解密 $(2n + 2)\left| {{G_2}} \right| + 2\left| {{G_1}} \right|$ $(n + 3)\left| {{G_2}} \right|$ $\left| {{G_2}} \right|$ -
SONG Xiaodong, WAGNER D, and PERRIG A. Practical techniques for searches on encrypted data[C]. 2000 IEEE Symposium on Security and Privacy, Berkeley, USA, 2000: 44–55. BONEH D, DI CRESCENZO G, OSTROVSKY R, et al. Public key encryption with keyword search[C]. International Conference on the Theory and Applications of Cryptographic Techniques, Interlaken, Switzerland, 2004: 506–522. LU Yang, WANG Gang, LI Jiguo, et al. Efficient designated server identity-based encryption with conjunctive keyword search[J]. Annals of Telecommunications, 2017, 72(5/6): 359–370. doi: 10.1007/s12243-017-0574-7 MIAO Yinbing, MA Jianfeng, LIU Ximeng, et al. VMKDO: Verifiable multi-keyword search over encrypted cloud data for dynamic data-owner[J]. Peer-to-Peer Networking and Applications, 2018, 11(2): 287–297. doi: 10.1007/s12083-016-0487-7 GE Xinrui, YU Jia, HU Chengyu, et al. Enabling efficient verifiable fuzzy keyword search over encrypted data in cloud computing[J]. IEEE Access, 2018, 6: 45725–45739. doi: 10.1109/ACCESS.2018.2866031 TURKY A, ABDULLAH S, and DAWOD A. A dual-population multi operators harmony search algorithm for dynamic optimization problems[J]. Computers & Industrial Engineering, 2018, 117: 19–28. doi: 10.1016/j.cie.2018.01.003 LI Yuxi, ZHOU Fucai, QIN Yuhai, et al. Integrity-verifiable conjunctive keyword searchable encryption in cloud storage[J]. International Journal of Information Security, 2018, 17(5): 549–568. doi: 10.1007/s10207-017-0394-9 FARRÀS O and RIBES-GONZÁLEZ J. Provably secure public-key encryption with conjunctive and subset keyword search[J]. International Journal of Information Security, 2019, 18(5): 533–548. doi: 10.1007/s10207-018-00426-7 WANG Haijiang, DONG Xiaolei, and CAO Zhenfu. Multi-value-independent ciphertext-policy attribute based encryption with fast keyword search[J]. IEEE Transactions on Services Computing, 2017(99): 1–11. doi: 10.1109/TSC.2017.2753231 SHIRAISHI Y, NOMURA K, MOHRI M, et al. Attribute revocable attribute-based encryption with forward secrecy for fine-grained access control of shared data[J]. IEICE Transactions on Information and Systems, 2017, E100. D(10): 2432–2439. doi: 10.1587/transinf.2016OFP0008 AMERI M H, DELAVAR M, MOHAJERI J, et al. A key-policy attribute-based temporary keyword search scheme for secure cloud storage[J]. IEEE Transactions on Cloud Computing, 2018(99): 1–12. doi: 10.1109/TCC.2018.2825983 张玉磊, 刘文静, 刘祥震, 等. 基于授权的多服务器可搜索密文策略属性基加密方案[J]. 电子与信息学报, 2019, 41(8): 1808–1814. doi: 10.11999/JEIT180944ZHANG Yulei, LIU Wenjing, LIU Xiangzhen, et al. Searchable Multi-server CP-ABE scheme based on authorization[J]. Journal of Electronics &Information Technology, 2019, 41(8): 1808–1814. doi: 10.11999/JEIT180944 MIAO Yinbin, MA Jianfeng, JIANG Qi, et al. Verifiable keyword search over encrypted cloud data in smart city[J]. Computers & Electrical Engineering, 2018, 65: 90–101. doi: 10.1016/j.compeleceng.2017.06.021 MIAO Yinbin, MA Jianfeng, WEI Fushan, et al. VCSE: Verifiable conjunctive keywords search over encrypted data without secure-channel[J]. Peer-to-Peer Networking and Applications, 2017, 10(4): 995–1007. doi: 10.1007/s12083-016-0458-z BALLARD L, KAMARA S, and MONROSE F. Achieving efficient conjunctive keyword searches over encrypted data[C]. The 7th International Conference on Information and Communications Security, Beijing, China, 2005: 414–426. TIWARI D and GANGADHARAN G R. SecCloudSharing: Secure data sharing in public cloud using ciphertext-policy attribute-based proxy re-encryption with revocation[J]. International Journal of Communication Systems, 2018, 31(5): e3494. doi: 10.1002/dac.3494 BHATEJA R, ACHARJYA D P, and SAXENA N. Enhanced timing enabled proxy re-encryption model for E-health data in the public cloud[C]. 2017 International Conference on Advances in Computing, Communications and Informatics (ICACCI), Udupi, India, 2017: 2040–2044. YANG Yang and MA Maode. Conjunctive keyword search with designated tester and timing enabled proxy Re-encryption function for E-health clouds[J]. IEEE Transactions on Information Forensics and Security, 2016, 11(4): 746–759. doi: 10.1109/TIFS.2015.2509912 WU Axin, ZHENG Dong, ZHANG Yinhui, et al. Hidden policy attribute-based data sharing with direct revocation and keyword search in cloud computing[J]. Sensors, 2018, 18(7): 2158. doi: 10.3390/s18072158 LI Jiguo, SHA Fengjie, ZHANG Yichen, et al. Verifiable outsourced decryption of attribute-based encryption with constant ciphertext length[J]. Security and Communication Networks, 2017, 2017: 3596205. doi: 10.1155/2017/3596205 赵志远, 孙磊, 户家富, 等. 可验证外包解密的离线/在线属性基加密方案[J]. 电子与信息学报, 2018, 40(12): 2998–3006. doi: 10.11999/JEIT180122ZHAO Zhiyuan, SUN Lei, HU Jiafu, et al. Efficient offline/online attribute based encryption with verifiable outsourced decryption[J]. Journal of Electronics &Information Technology, 2018, 40(12): 2998–3006. doi: 10.11999/JEIT180122 LYNN B. PBC library[EB/OL]. http://cryptostanford.edu/pbc, 2006. -





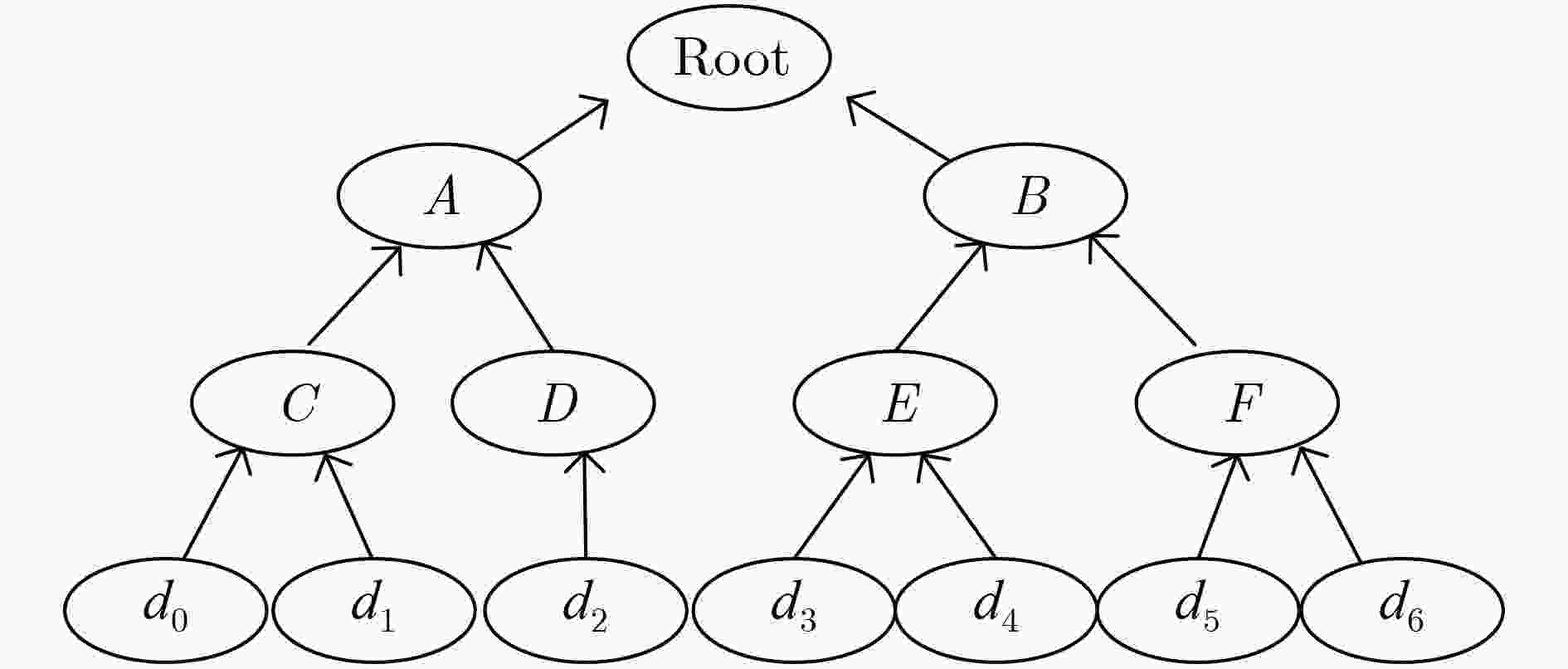
 下载:
下载:

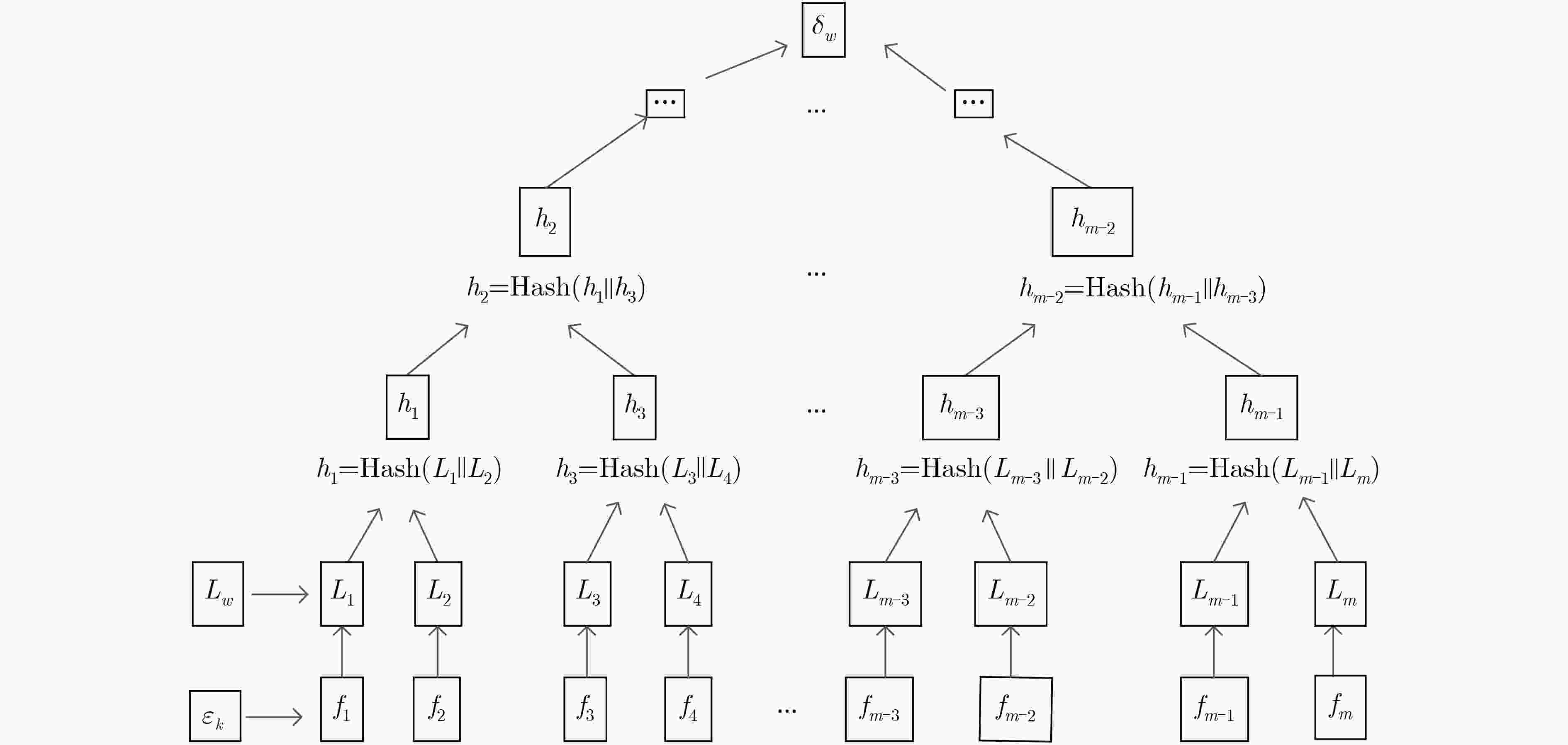
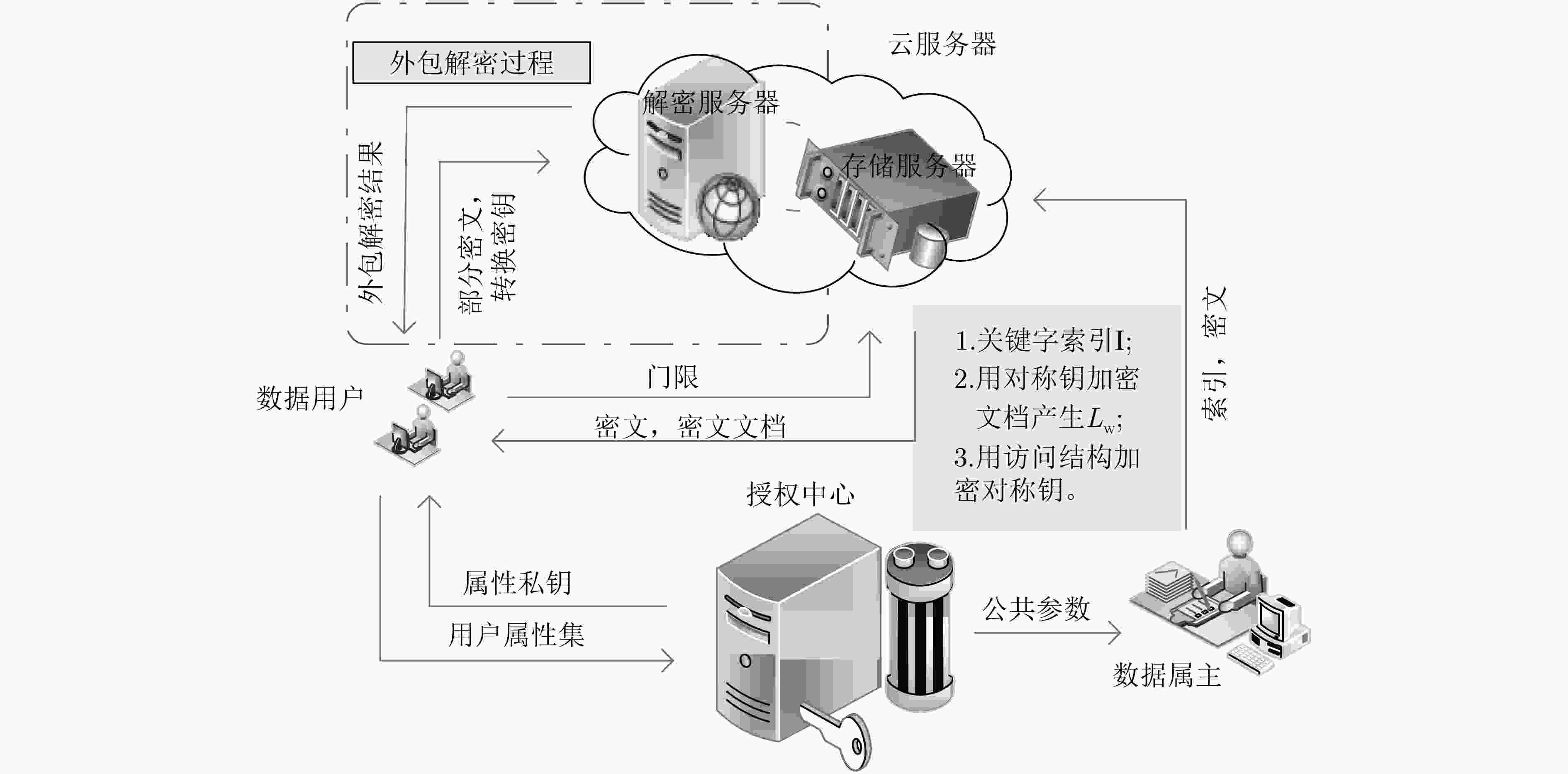
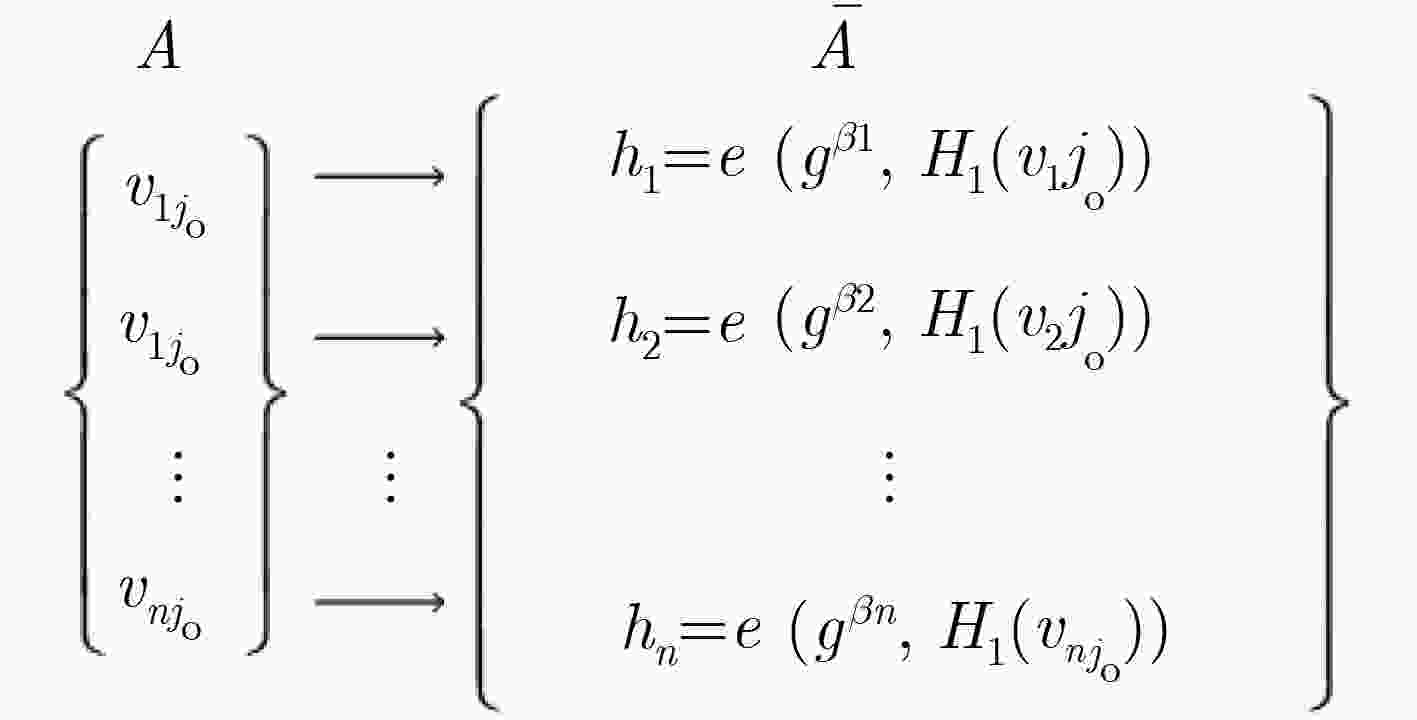
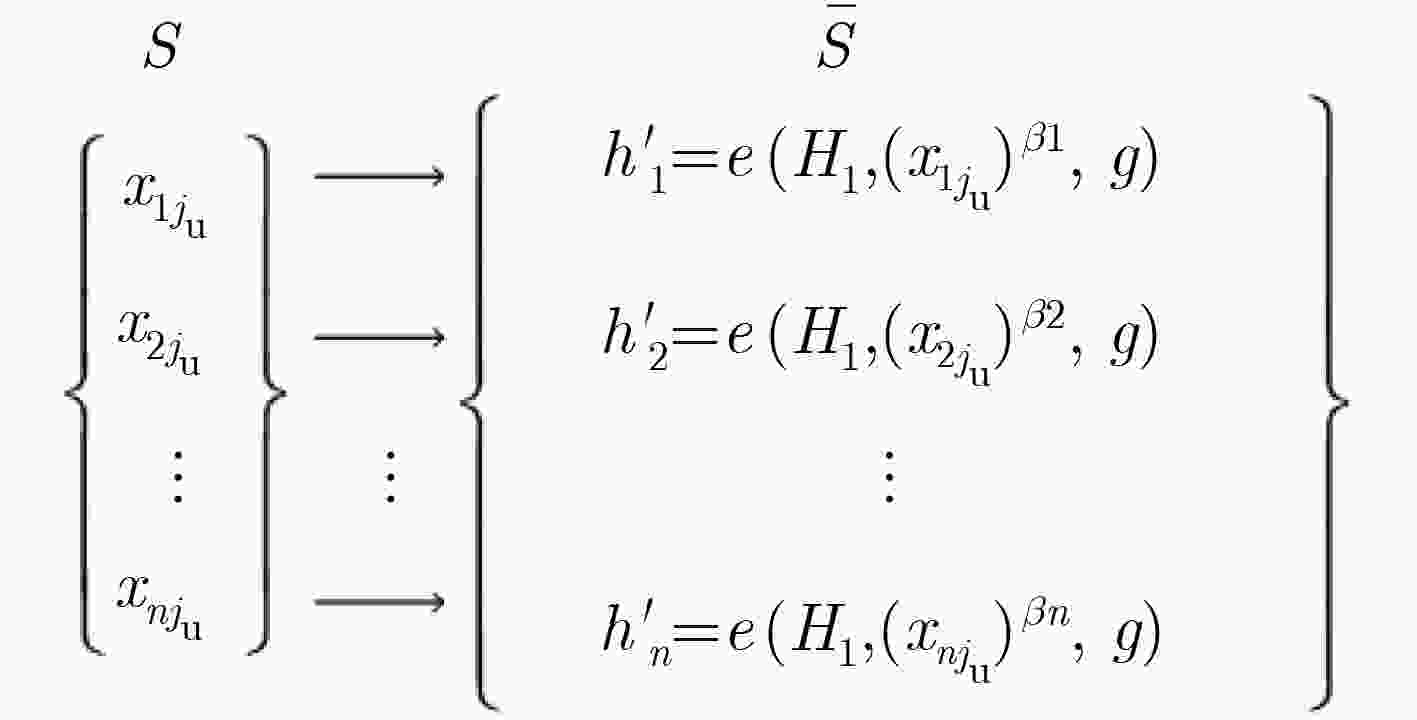
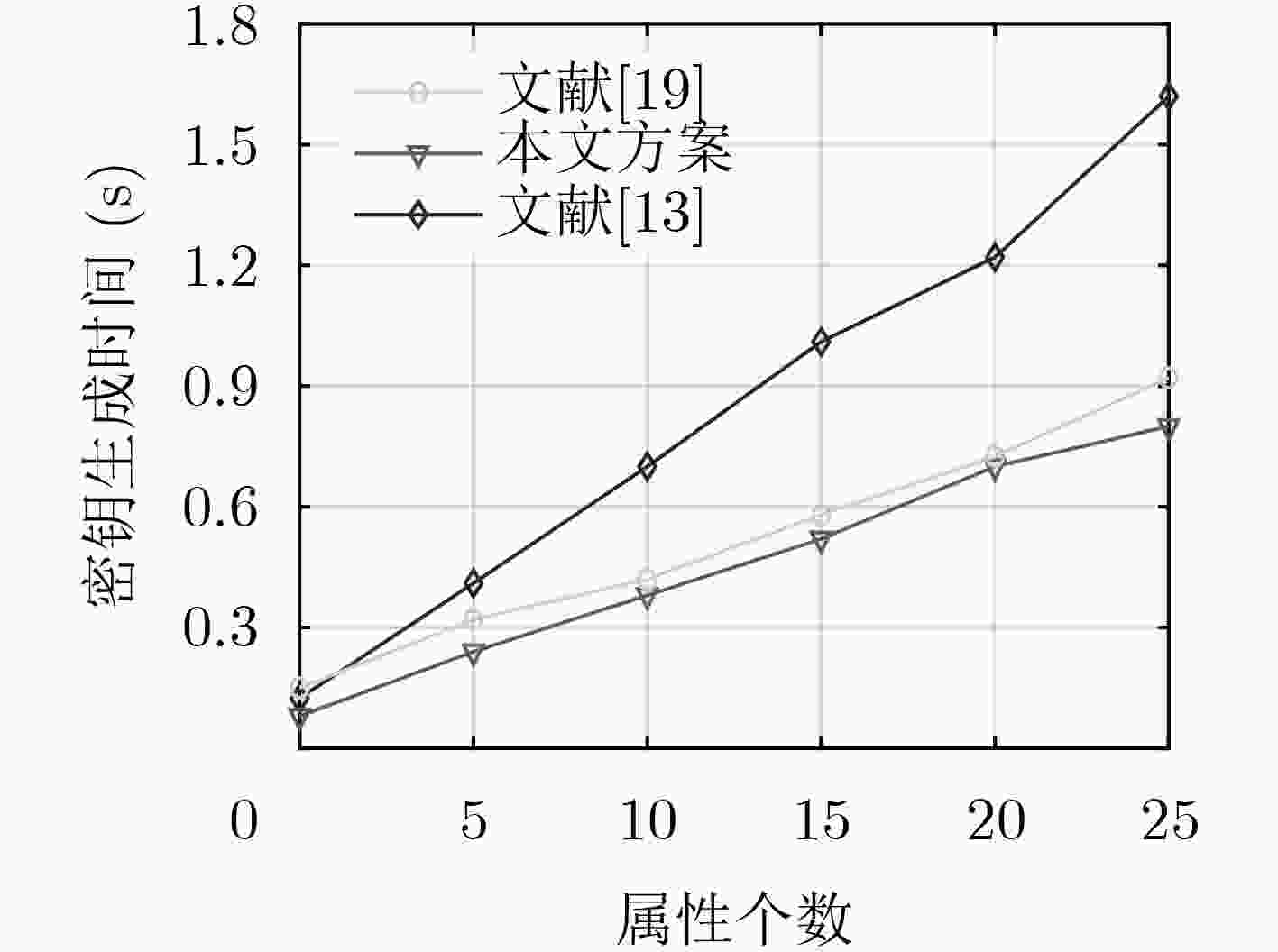
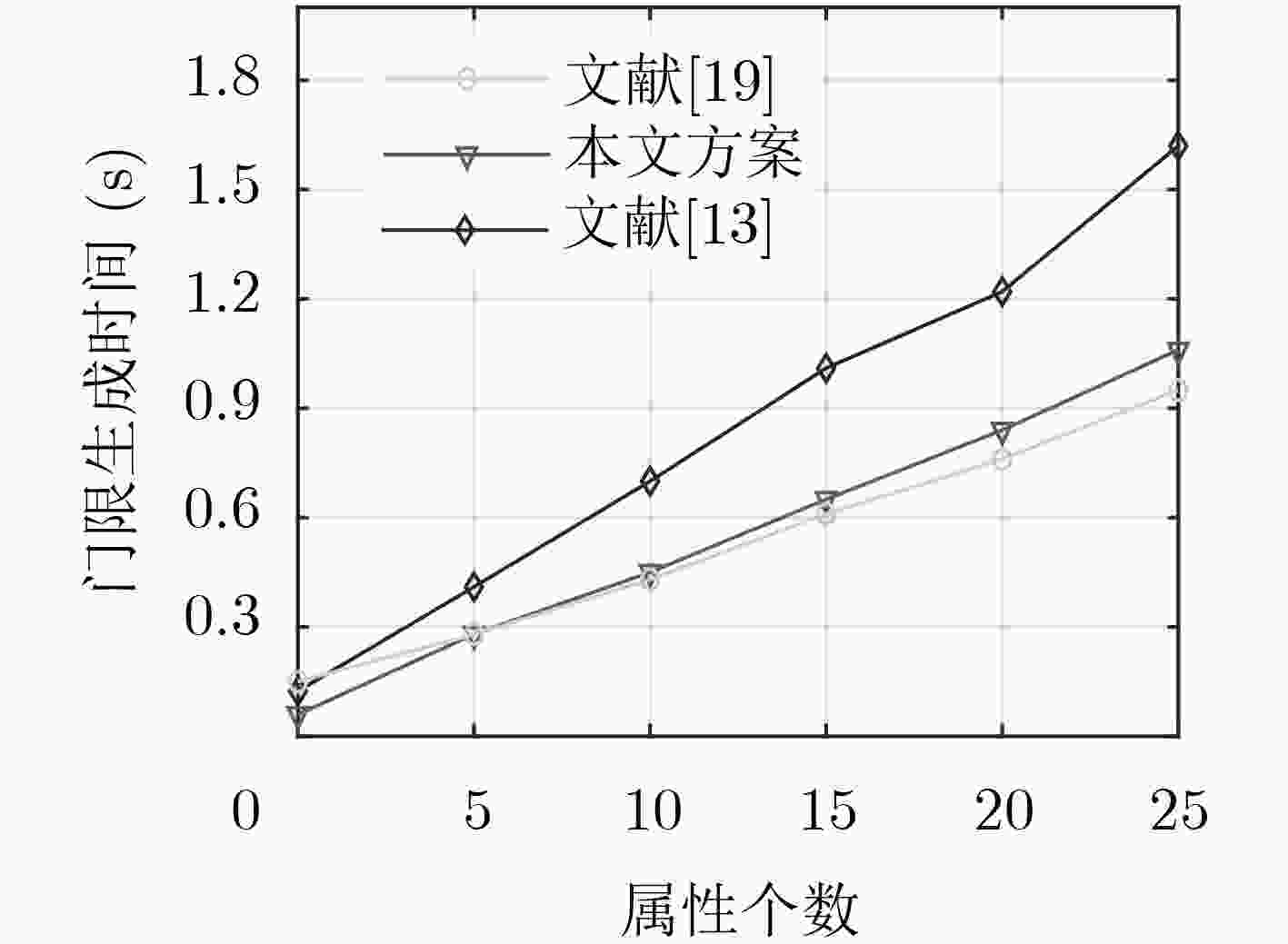
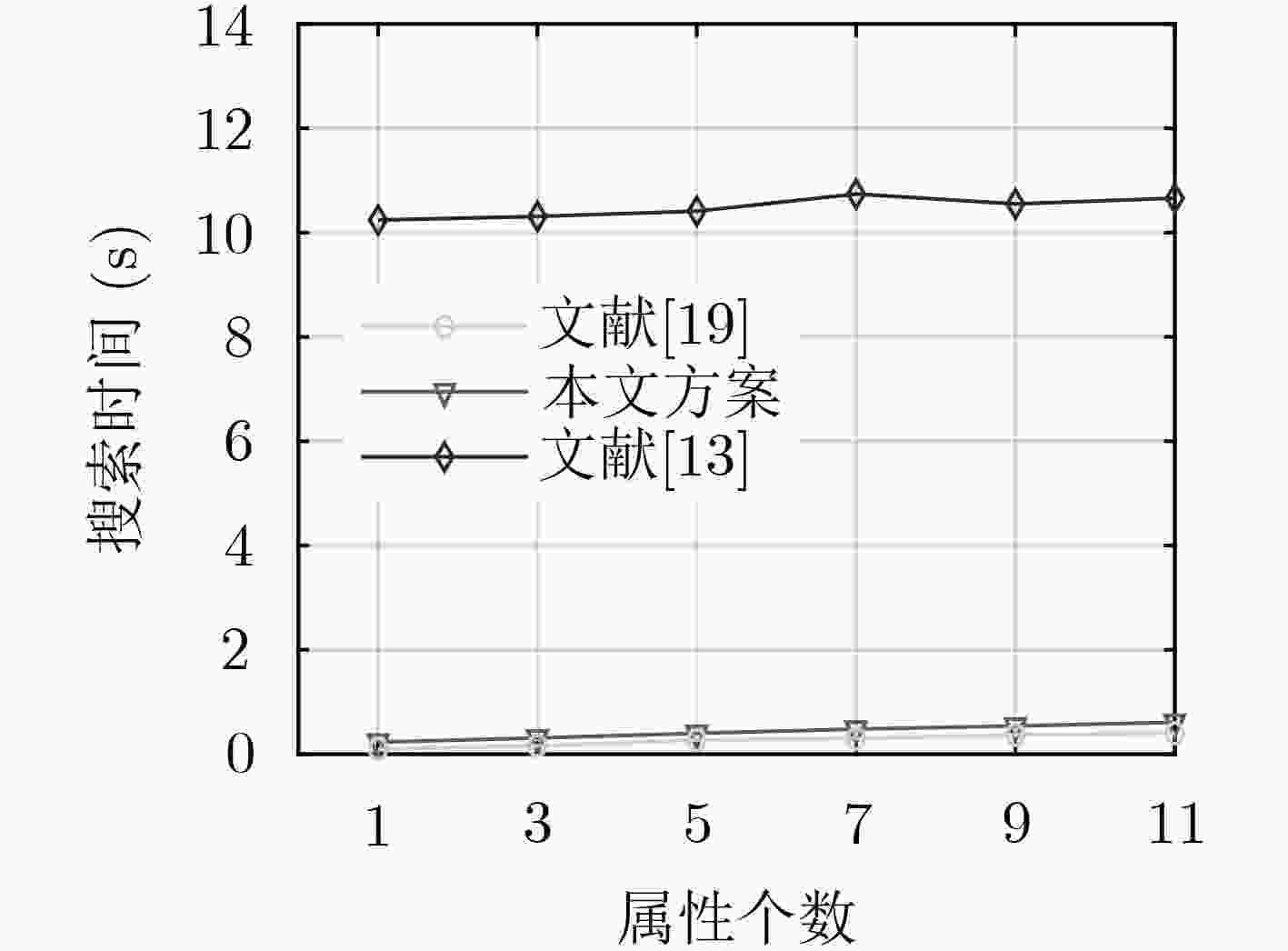
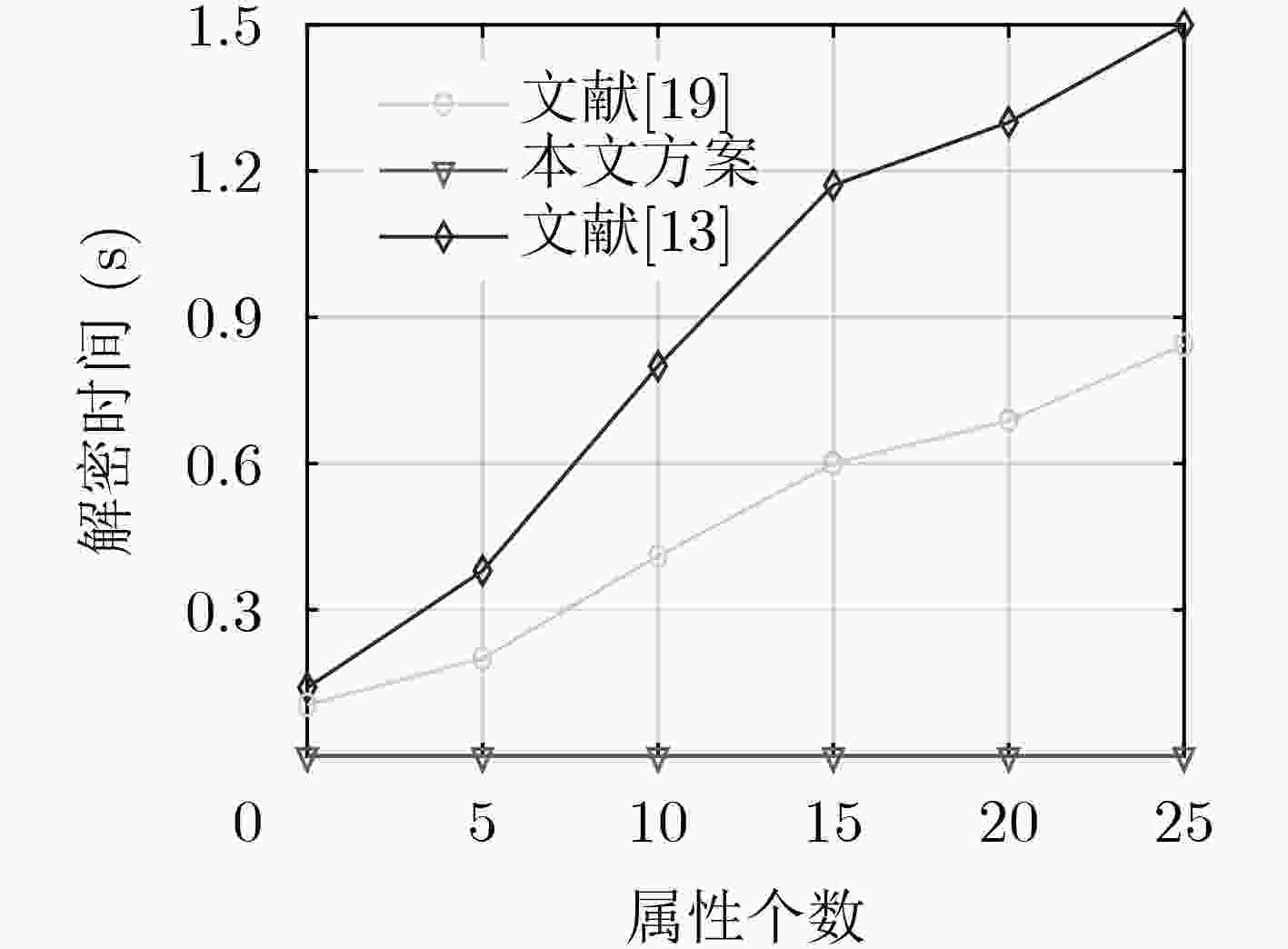
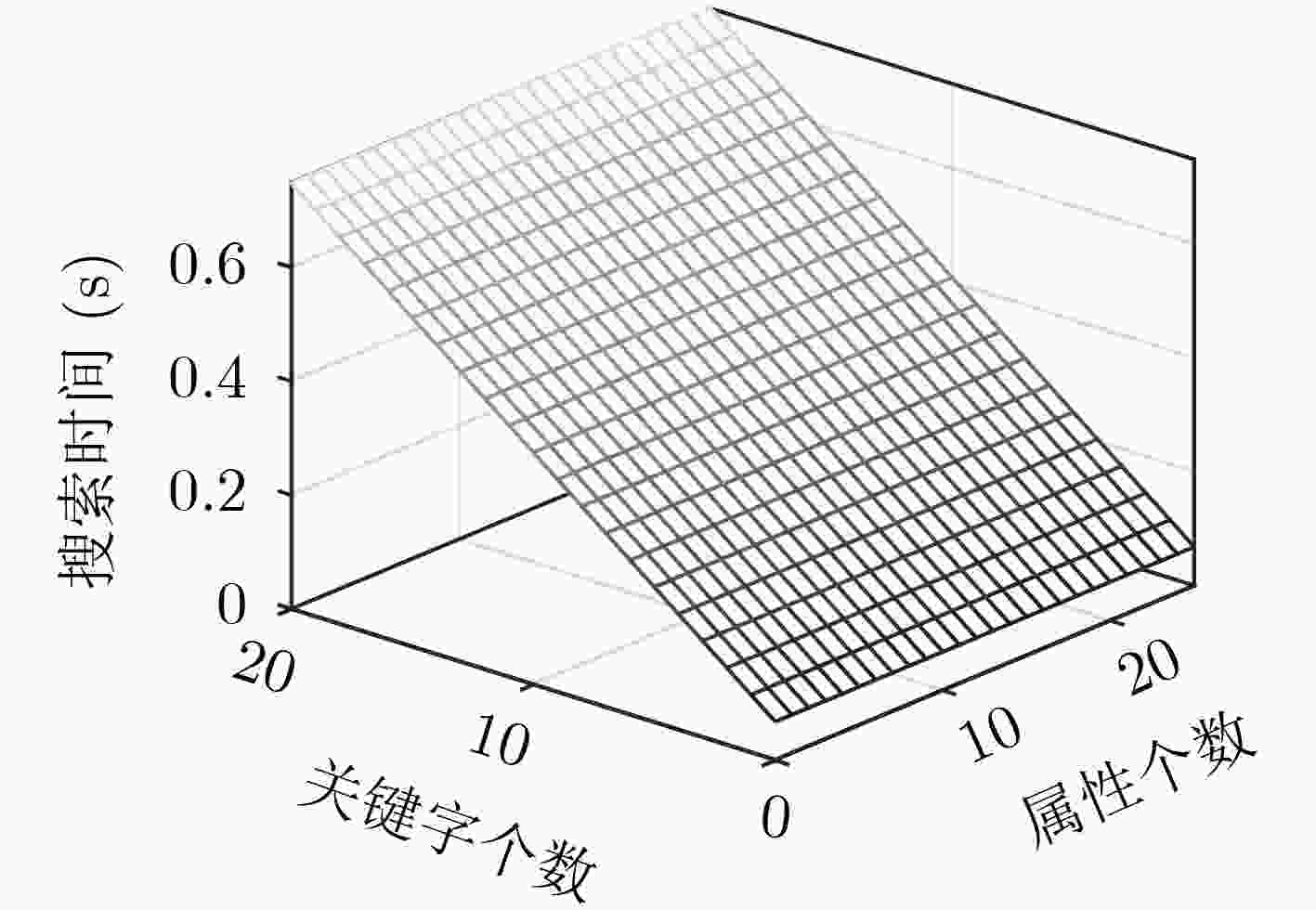
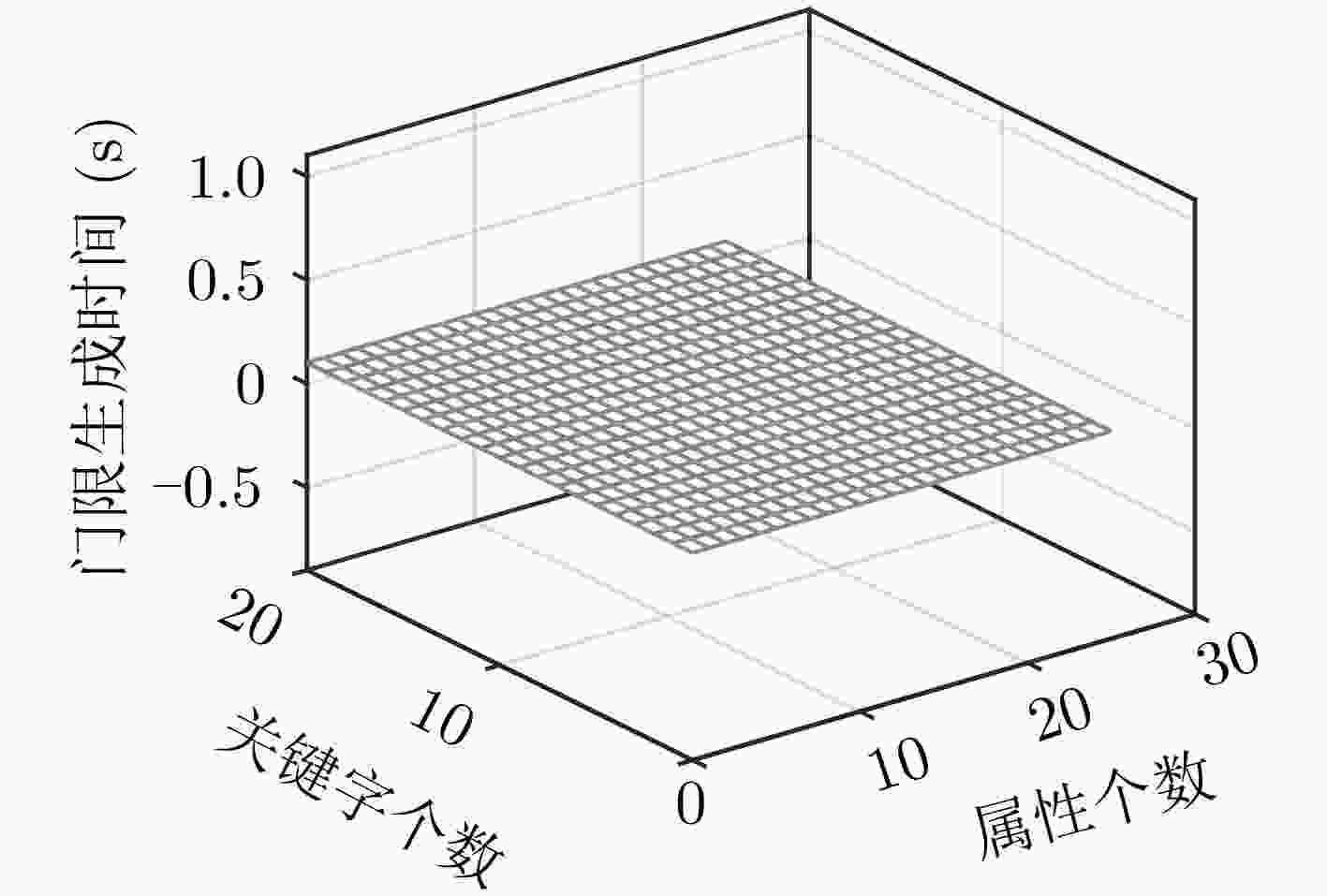


 下载:
下载:
