Blockchain User Anonymity and Traceability Technology
-
摘要: 区块链具有透明性、数据完整性、防篡改等优点，在金融、政府、军事等领域有重要应用价值。目前有越来越多的工作研究区块链的隐私保护问题，典型的包括门罗币、Zerocash, Mixcoin等等。这些隐私保护方法可以用于保护区块链上用户的身份和交易的金额。隐私保护方案是双刃剑，一方面是对合法用户隐私的完善保护，另一方面如果完全脱离监管，则是对洗钱、勒索等违法犯罪行为的姑息和纵容。针对区块链上各种层出不穷的隐私保护方案，监管也要与时俱进。该文研究区块链用户身份的隐私保护和监管方法，提出了用户匿名和可追踪的技术，旨在推动区块链在实际中的应用。Abstract: Blockchain has the advantages of transparency, data integrity, tamper resistance, etc., and has important application value to the fields of finance, government, and military. There are many work to study the privacy protection of the blockchain, typically including Monero, Zerocash, Mixcoin, and more. Their privacy protection methods can be used to protect the identity of the user and the amount of the transaction. The privacy protection scheme is a double-edged sword. On the one hand, it is the perfect protection of the privacy of legitimate users. On the other hand, if it is completely out of supervision, it is the appeasement and connivance of illegal crimes such as money laundering and extortion. In response to the various endangered privacy protection schemes on the blockchain, regulation must also keep pace with the times. In view of this, the privacy protection and supervision methods of blockchain user’s identity is studied, and anonymity and traceability technology to promote the application of blockchain to practice is proposed.
-
Key words:
- Blockchain /
- Anonymity /
- Traceability /
- Group signature
-
1. 引言
星地融合网络(Integrated Satellite-Terrestrial Networks, ISTNs)具有覆盖范围广、传输数据通量高、可连接用户数多和抗毁性强等特性，是在遇到地震、台风等极端自然灾害之后重建通信链路的最有效途径[1]。近年来，随着物联网(Internet-of-Things, IoT)、车联网(Internet-of-Vehicles, IoV)、远程医疗等其他技术的快速发展和急切需求，星地融合网络在学术界和工程领域都获得了巨大的关注[2]。
服务质量(Quality of Service, QoS)和频谱效率是未来星地融合网络发展的两个关键因素。因此，为了提高频谱效率并增强用户的服务体验，非正交多址接入(Non-Orthogonal Multiple Access, NOMA)技术被引入到星地融合网络中[3]。NOMA技术采用功率域多址方案，实现利用同一频率资源向多个传感器用户传输内容的目的，从而提高频谱效率，并通过功率分配因子提高传感器用户的服务质量，这有别于传统的正交多址接入( Orthogonal Multiple Access, OMA)技术[4]。由于NOMA技术的优越性，许多研究分析了将NOMA技术应用于卫星通信(Satellite Communication, SatCom)后对于系统性能的提升。文献[5]研究了 NOMA辅助的星地融合网络的中断性能，并推导得到了系统的中断概率(Outage Probability, OP)的闭式解析表达式和渐近表达式。文献[6]建立了基于NOMA的卫星通信系统的功率分配优化模型，提高了传感器用户的服务质量。文献[7]将NOMA方案应用于基于内容分发的星地融合网络，并推导得到了中断概率和命中概率的解析表达式。
多天线技术同样是增强系统传输质量的关键技术。相比基于单天线的NOMA系统，多天线技术的应用可以有效提高系统的容量[8]。文献[9]研究了多天线节点下的星地融合中继网络(Integrated Satellite-Terrestrial Relay Network, ISTRN)的性能，并验证了多天线技术对于系统性能提升的积极影响。文献[10]通过分析比较得出了多天线星地融合网络的中断概率更优。文献[11]讨论了多天线星地融合网络的可靠性和安全性，并通过数值结果验证了多天线技术的优越性。
在实际条件的影响下，基于NOMA的星地融合网络在传输和检测过程中会受到各种非完美因素的影响。在传输过程中，信道通常会经历严重的衰落，如雨、雾等天气的影响，因此，系统很难获得完美的信道状态信息(Channel State Information, CSI)[12]。同时由于信道估计技术的限制，信道估计误差(Channel Estimation Errors, CEEs)不可避免地会出现在信道状态信息估计过程中[13]。文献[14]在陆地移动卫星系统中考虑了不完美CSI，推导得到了系统的精确和渐近中断概率。文献[15]建立了非理想CSI下的卫星通信系统模型，并推导得到了系统的最优能量利用效率。此外，在卫星信号接收检测过程中，NOMA用户采用串行干扰消除(Successive Interference Cancellation, SIC)技术来获取叠加信号中每个传感器用户的目标信号[16]。然而，由于接收器性能的限制，实际条件下很难实现完美的串行干扰消除[17]。文献[18]分析了在非完美SIC下的基于NOMA的卫星通信系统性能，推导得出了每个传感器用户中断概率和渐近中断概率的解析表达式。然而，作者采用了一个独立的干扰因子来表示非完美SIC的影响，缺乏系统性的理论分析。此外，由于频谱资源的重复利用，同频干扰(Co-Channel Interference, CCI)同样会出现在信号传输过程中[19]。文献[20]分别从遍历容量(Ergodic Capacity, EC)、中断概率、平均符号错误率和能量效率等方面评估了同频干扰对星地融合网络的影响。
针对以上问题，本文在非完美条件下，即信道估计误差，非完美SIC和同频干扰的影响下，对基于NOMA的星地融合网络的遍历容量性能进行了研究。本文的主要贡献如下：(1)建立了非完美条件下的星地融合NOMA网络的系统模型。由于接收机性能的限制，串行干扰消除是非完美的。由于非完美的信道状态信息，考虑了信道估计误差。同时，频率的重复利用导致了同频干扰。(2)通过遍历容量性能的理论推导，刻画了不同非完美条件参数对于星地融合NOMA网络的影响。(3)采用蒙特卡罗仿真进一步验证了遍历容量性能理论推导的正确性。
2. 系统模型和问题建模
如图1所示，本文考虑一个基于NOMA的多天线星地融合网络，其中地球同步卫星(Geosynchronous Earth Orbit, GEO)信号源
S 采用NOMA技术通过直连链路与地面的传感器用户Ui,i∈(1,2,⋯,p,q,⋯,N) 进行通信。地面传感器用户通过分组策略分为多个簇，不失一般性，本文针对一个卫星波束下的两个NOMA用户Ui,i∈(p,q) 进行分析。两用户NOMA场景被3GPP(Third Generation Partnership Project)组织认可为可以增强传感器用户的频谱效率。因此，采用两用户NOMA方案，不仅可以简化系统模型并可以为未来研究多NOMA传感器用户场景提供基础[5]。此外，假设两个地面传感器用户位于卫星多个波束中的同一个波束内。地面传感器用户为了增强天线增益配置了M 根天线。同时，由于地面设备频率复用，每一个传感器用户都会受到Ic,c∈{1,2,⋯,N} 个干扰的影响。2.1 信道模型
在星地融合网络中，采取阵列馈电反射(Array Fed Reflector, AFR)技术固定每个天线的辐射模式来减少控制系统的处理消耗。相比较直接辐射阵列(Direct Radiating Array, DRA)技术，阵列馈电反射技术可以获得更高的天线增益和能量效率[6]。考虑到自由空间损耗、雨衰和天线增益，星地链路的信道分量表达式为
hSUi=√FiHiζi−12⋅f12igSUi (1) 其中，
Fi 代表自由空间损耗，并可以表示为Fi = (Vf)21d2G+d2i (2) 其中，
V = c/c4π 4π ，c 代表电磁波速度，f 代表载波频率，dG≈35786 km 代表GEO卫星高度，di 代表传感器用户Ui 到卫星波束覆盖范围中心的距离。Hi 代表地面传感器用户Ui 的天线增益，表达式为Hi≃{Hmax−2.5×10−3(daθλ)2,0∘<θ<θa2+15lgdaλ,θa<θ<θb32−25lgθ,θb<θ<48∘−10,48∘<θ<180∘ (3) 其中，
Hmax 代表用户天线的最大增益，da 代表天线直径，λ 代表信号波长，θ 代表离轴角度，其中θa=20λda√Hmax−(2+15lgdaλ) ,θb=15.85×(da/λ)−0.6 。此外，ζi = [ζi.1,ζi.2,⋯,ζi.M]T 代表雨衰分量，ζi.m∼CN(μ,δ2ζ) 服从对数随机分布，m∈{M} 。fi = [fi.1,fi.2,⋯,fi.M]T 代表卫星天线增益向量，其中fi.m 表达式为fi.m≃fmax(B1(ri,m)2ri,m+36B3(ri,m)r3i,m)2 (4) 其中，
fmax 代表卫星天线最大增益，B1(⋅) 和B3(⋅) 分别表示次序1和3的第1类贝塞尔函数。ri,m=τsinφi,m/τsinφi,msinφ3dBsinφ3dB ,τ=2.07123 ，其中φi,m 代表第m 个天线波束中心与用户Ui 和卫星直连线路中心的夹角，φ3dB 代表3 dB角度。最后，gSUi 代表星地链路随机信道分量。目前存在许多的数学模型表示星地链路信道信息，例如Lutz模型、Markov模型以及Karasaw模型。本文采用阴影莱斯(Shadowed-Rician, SR)模型来描绘星地信道。SR分布的模型与实测数据十分吻合，同时计算复杂度相对较低。因此很多文献采用SR分布作为星地融合网络信道模型[5]。根据SR分布，gSUi 的第m 个分量可以表示为gSUi,m=Xexp(jς)+Yexp(jϑ) (5) 其中，
X 和Y 均是独立平稳随机过程，并分别代表直连链路和多径分量的振幅。直连链路和多径分量分别服从Nakagami-m 分布和瑞利分布。ς 代表直连链路的确定性分量，ϑ 代表平稳随机分量，并服从[0,2π) 。通过数学转换，
gSUi,m 的平方振幅的概率密度函数(Probability Density Function, PDF)可以表示为f‖ (6) 其中，
{\alpha _{{\text{S}}{{\text{U}}_i},m}}{\text{ }} \triangleq {\text{ }}\dfrac{{{{\left( {\dfrac{{2{b_{{\text{S}}{{\text{U}}_i},m}}{m_{{\text{S}}{{\text{U}}_i},m}}}}{{2{b_{{\text{S}}{{\text{U}}_i},m}}{m_{{\text{S}}{{\text{U}}_i},m}} + {\varOmega _{{\text{S}}{{\text{U}}_i},m}}}}} \right)}^{{m_{{\text{S}}{{\text{U}}_i},m}}}}}}{{2{b_{{\text{S}}{{\text{U}}_i},m}}}} ,{\delta _{{\text{S}}{{\text{U}}_i},m}} \triangleq \dfrac{{{\varOmega _{{\text{S}}{{\text{U}}_i},m}}}}{{2{b_{{\text{S}}{{\text{U}}_i},m}}\left( {2{b_{{\text{S}}{{\text{U}}_i},m}}{m_{{\text{S}}{{\text{U}}_i},m}} + {\varOmega _{{\text{S}}{{\text{U}}_i},m}}} \right)}} ,{\beta _{{\text{S}}{{\text{U}}_i},m}} \triangleq \dfrac{1}{{2{b_{{\text{S}}{{\text{U}}_i},m}}}} ,{\varOmega _{{\text{S}}{{\text{U}}_i},m}},2{b_{{\text{S}}{{\text{U}}_i},m}} 和{m_{{\text{S}}{{\text{U}}_i},m}} \in (0,\infty ) 分别代表直连分量的平均功率，多径分量的平均功率和衰落程度。假设
{m_{{\text{S}}{{\text{U}}_i},m}} 为正整数，通过代数变换[21]，概率密度函数可以重新表示为\begin{split} {f_{{{\left\| {{g_{{\text{S}}{{\text{U}}_i},m}}} \right\|}^2}}}\left( x \right) =& {\alpha _{{\text{S}}{{\text{U}}_i},m}}\sum\limits_{k = 0}^{{m_{{\text{S}}{{\text{U}}_i},m}} - 1} {\zeta \left( k \right)} {x^k}\\ & \cdot{{\rm{e}}^{ - \left( {{\beta _{{\text{S}}{{\text{U}}_i},m}} - {\delta _{{\text{S}}{{\text{U}}_i},m}}} \right)x}} \end{split} (7) 其中，
\zeta \left( k \right) = {\left( { - 1} \right)^k}{\left( {1 - {m_{{\text{S}}{{\text{U}}_i},m}}} \right)_k}\delta _{{\text{S}}{{\text{U}}_i},m}^k/{\left( {k!} \right)^2} 。{\left( \cdot \right)_k} 代表Pochhammer符号。2.2 信号模型
S 采用叠加编码技术将叠加信号发送给两个地面传感器用户{U_i} ，信号表达式为x = \sqrt {{a_p}} {s_p} + \sqrt {{a_q}} {s_q} (8) 其中，
{s_i} 代表不同用户的目标信号，并满足{\rm{E}}[|{s_i}{|^2}] = 1 。{a_i} 是NOMA技术中的不同信号的功率分配系数，并满足{a_p} + {a_q} = 1 。本场景假设用户{U_p} 相比{U_q} 经历更严重的衰落，因此，更多的信号功率将分配给信道状态更差的用户，即{a_p} > {a_q} 。因此，用户接收到的信号可以表示为\begin{split} {y_i} =& {{\boldsymbol{h}}_{{\text{S}}{{\text{U}}_i}}}{\boldsymbol{w}}_1^{\rm{H}}\sqrt {{P_{\text{S}}}} (\sqrt {{a_p}} {s_p} + \sqrt {{a_q}} {s_q}) \\ & + \sum\limits_{I = 1}^N {{{\boldsymbol{g}}_{iI}}{\boldsymbol{w}}_1^{\rm{H}}\sqrt {{P_{\text{I}}}} {s_{iI}}} + {\boldsymbol{w}}_1^{\rm{H}}{{\boldsymbol{n}}_i} \end{split} (9) 其中，
{P_{\text{S}}} 代表卫星信号的传输功率，{P_{\text{S}}} = \sigma P ，P 代表卫星整体功率，\sigma \in \left( {0,1} \right) 代表功率系数。{{\boldsymbol{h}}_{{\text{S}}{{\text{U}}_i}}} 代表卫星和用户间的信道分量，满足SR分布。\left\| {{{\boldsymbol{w}}_1}} \right\| = 1 代表波束成形分量。{s_{iI}} 代表干扰信号，{P_{\text{I}}} 代表干扰信号功率。{{\boldsymbol{g}}_{iI}} 代表干扰和用户之间的信道分量，服从瑞利分布[9]。{{\boldsymbol{n}}_i} 代表卫星和用户之间的加性高斯白噪声并服从{n_{i,m}}{\text{～}}\rm{C}\rm{N}\left( {0,\delta _{i,m}^2} \right) 。\delta _{i,m}^2 = {{\rm{K}}_{\rm{B}}}{T_i} ,{{\rm{K}}_{\rm{B}}} = 1.380649 \times {10^{ - 23}}\;{\rm{J}}/{\rm{K}} 代表Boltzmann常数，{T_i} 代表用户噪声温度。2.3 问题建模
考虑到实际系统条件，星地链路的电磁环境和气候环境极其复杂，导致系统无法获得完美的CSI。因此在信道估计过程中会产生信道估计误差。采用均方误差算法，信道估计模型可以表示为
{h_{{\text{S}}{{\text{U}}_i},m}} = {\tilde h_{{\text{S}}{{\text{U}}_i},m}} + {e_{{\text{S}}{{\text{U}}_i},m}} (10) 其中，
{h_{{\text{S}}{{\text{U}}_i},m}} 代表星地链路的SR分布的实际振幅，{\tilde h_{{\text{S}}{{\text{U}}_i},m}} 代表星地链路的SR分布的检测振幅，{e_{{\text{S}}{{\text{U}}_i},m}} 代表星地链路的信道估计误差。{\tilde h_{{\text{S}}{{\text{U}}_i},m}} 和{e_{{\text{S}}{{\text{U}}_i},m}} 相互正交。{e_{{\text{S}}{{\text{U}}_i},m}} 服从复杂高斯分布，即{e_{{\text{S}}{{\text{U}}_i},m}}{\text{～}} {\rm{CN}} \left( {0,{{ \mathcal{\overline V} }_{{e_{{\text{S}}{{\text{U}}_i},m}}}}} \right) 。采用导频符号来估计星地链路的信道状态信息，则{e_{{\text{S}}{{\text{U}}_i},m}} 的方差可以表示为\begin{split} {{ \mathcal{\overline V} }_{{e_{{\text{S}}{{\text{U}}_i},m}}}} &= {\rm{E}}\left\{ {{{\left| {{h_{{\text{S}}{{\text{U}}_i},m}}} \right|}^2}} \right\} - {\rm{E}}\left\{ {{{\left| {{{\tilde h}_{{\text{S}}{{\text{U}}_i},m}}} \right|}^2}} \right\} \\ & = \frac{1}{{{\mathcal{L}_{{\text{S}}{{\text{U}}_i},m}}{{ \mathcal{\overline V} }_{{\text{S}}{{\text{U}}_i},m}} + 1}} \end{split} (11) 其中，
{\mathcal{L}_{{\text{S}}{{\text{U}}_i},m}} 代表导频符号长度，{ \mathcal{\overline V} _{{\text{S}}{{\text{U}}_i},m}} 代表导频符号在星地链路的平均信噪比。将{ \mathcal{\overline V} _{{\text{S}}{{\text{U}}_i},m}} 写作最小均方误差形式为{ \mathcal{\overline V} _{{\text{S}}{{\text{U}}_i},m}} = {\rm{E}}\left\{ {{\mathcal{V}_{{\text{S}}{{\text{U}}_i},m}}} \right\} = {P_{\text{e}}}E\left\{ {{{\left| {{h_{{\text{S}}{{\text{U}}_i},m}}} \right|}^2}} \right\}/\delta _{i,m}^2 (12) 其中，
{P_{\text{e}}} 代表导频符号功率，{P_{\text{e}}} = \left( {1 - \sigma } \right)P 。本文采用{ \mathcal{\overline V} _{{e_{{\text{S}}{{\text{U}}_i},m}}}} 来表示系统的信道估计误差。传感器用户通过最大比合并技术来增强星地融合网络的性能，其表达式为
{{\boldsymbol{w}}_1} = \frac{{{{\boldsymbol{h}}_{{\text{SU}}}}}}{{{{\left\| {{{\boldsymbol{h}}_{{\text{SU}}}}} \right\|}^2}}} (13) 根据上述分析，可以推导得到，在用户
{U_q} 处检测信号{s_p} 的信干噪比为{\gamma _{{\text{S}}{{\text{U}}_{q - p}}}} = \frac{{{a_p}\sigma {\lambda _{{\text{S}}{{\text{U}}_q}}}}}{{{a_q}\sigma {\lambda _{{\text{S}}{{\text{U}}_q}}} + \sigma {{\overline V }_{{e_{{\text{S}}{{\text{U}}_q}}}}} + {\lambda _{{l_q}}} + 1}} (14) 其中，
{\lambda _{{\text{S}}{{\text{U}}_q}}} = {\left| {{{\tilde {\boldsymbol{h}}}_{{\text{S}}{{\text{U}}_q}}}{\boldsymbol{w}}_1^{\rm{H}}} \right|^2}P/\delta _q^2 = {\bar \gamma _{{\text{S}}{{\text{U}}_q}}}{\left\| {{{\tilde {\boldsymbol{h}}}_{{\text{S}}{{\text{U}}_q}}}} \right\|^2} ,{\bar \gamma _j} ,j \in \left\{ {{\text{S}}{{\text{U}}_p},{\text{S}}{{\text{U}}_q}} \right\} 代表卫星到不同用户的平均信噪比。{\lambda _{{l_q}}} = \displaystyle\sum\nolimits_{c = 1}^N {{{\left| {{{\boldsymbol{g}}_{lq}}{\boldsymbol{w}}_1^{\rm{H}}} \right|}^2}{P_l}/\delta _q^2} = {\bar \gamma _q}\sum\nolimits_{c = 1}^N {{{\left\| {{{\boldsymbol{g}}_{lq}}} \right\|}^2}} ,{\bar \gamma _i} ,i \in \left\{ {p,q} \right\} 代表干扰到不同用户的平均信噪比。在NOMA方案中，采用SIC技术来检测和接收信号，用户
{U_q} 先检测信号{s_p} ，将其分离后再检测目标信号{s_q} 。但由于接收机性能的限制，假设非完美SIC在接收端产生，此时，{U_q} 处检测信号{s_q} 的信干噪比为{\gamma _{{\text{S}}{{\text{U}}_q}}} = \frac{{{a_q}\sigma {\lambda _{{\text{S}}{{\text{U}}_q}}}}}{{{a_p}\xi \sigma {\lambda _{{\text{S}}{{\text{U}}_q}}} + \sigma {{\overline V }_{{e_{{\text{S}}{{\text{U}}_q}}}}} + {\lambda _{{l_q}}} + 1}} (15) 其中，
\xi 代表非完美SIC系数，满足\xi \in \left( {0,1} \right) 。最后，本文在
{U_p} 处检测信号{s_p} ，将信号{s_q} 直接视作干扰，则信干噪比为{\gamma _{{\text{S}}{{\text{U}}_p}}} = \frac{{{a_p}\sigma {\lambda _{{\text{S}}{{\text{U}}_p}}}}}{{{a_q}\sigma {\lambda _{{\text{S}}{{\text{U}}_p}}} + \sigma {{\overline V }_{{e_{{\text{S}}{{\text{U}}_p}}}}} + {\lambda _{{l_p}}} + 1}} (16) 其中，
{\lambda _{{\text{S}}{{\text{U}}_p}}} = {\left| {{{\tilde {\boldsymbol{h}}}_{{\text{S}}{{\text{U}}_p}}}{\boldsymbol{w}}_1^{\rm{H}}} \right|^2}P/\delta _p^2 = {\bar \gamma _{{\text{S}}{{\text{U}}_p}}}{\left\| {{{\tilde {\boldsymbol{h}}}_{{\text{S}}{{\text{U}}_p}}}} \right\|^2} ,{\lambda _{{l_p}}} = \displaystyle\sum\nolimits_{c = 1}^N {{{\left| {{{\boldsymbol{g}}_{lp}}{\boldsymbol{w}}_1^{\rm{H}}} \right|}^2}{P_l}/\delta _p^2} = {\bar \gamma _p}\sum\nolimits_{c = 1}^N {{{\left\| {{{\boldsymbol{g}}_{lp}}} \right\|}^2}} 。值得说明的是文献[14,15,18,20]都只是分析了非完美条件的特例。本文采用导频信号来估计信道估计误差，这有别于文献[14]。在此基础上，考虑了服从瑞利分布的同频干扰。此外，在文献[18]中，非完美的SIC干扰被看作一个独立的参数，本文将非完美SIC与实际信号处理过程相关联。由此可知，本文所研究的非完美条件与之前所研究的文章有很大区别。
3. 性能分析
本节首先将会给出阴影莱斯信道和瑞利信道的信道统计特征的概率密度函数和累积分布函数(Cumulative Distribution Function, CDF)，在此基础上，将推导得到系统遍历容量的闭式解。
3.1 信道统计特征
星地链路服从阴影莱斯分布，在最大比合并技术的基础上，
{\gamma _j} = {\bar \gamma _j}{\left| {{h_j}} \right|^2} 的概率密度函数为{f_{{\gamma _j}}}\left( x \right) = \frac{{\alpha _j^{{M}}}}{{\varGamma \left( {{M}} \right)}}\sum\limits_{k = 0}^{{{M}}\left( {{m_j} - 1} \right)} {\frac{{\zeta {{\left( k \right)}_{{M}}}}}{{{{\left( {{{\bar \gamma }_j}} \right)}^{k + {{M}}}}}}{x^{k + {{M}} - 1}}{{\rm{e}}^{ - {\varDelta _j}x}}} (17) 其中，
{\varDelta _j} = {{{\beta _j} - {\delta _j}} \mathord{\left/ {\vphantom {{{\beta _j} - {\delta _j}} {{{\bar \gamma }_j}}}} \right. } {{{\bar \gamma }_j}}} 。经过数学变换[21]，
{\gamma _j} 的累积分布函数为\begin{split} {F_{{\gamma _j}}}\left( x \right) =& 1 - \frac{{\alpha _j^{{M}}}}{{\varGamma \left( {{M}} \right)}}\\ & \cdot\sum\limits_{{k_j} = 0}^{{{M}}({m_j} - 1)} {\sum\limits_{t = 0}^{{k_j}} {\frac{{{{\left( {{{M}}\left( {1 - {m_j}} \right)} \right)}_{{k_1}}}{{\left( { - {\delta _j}} \right)}^{{k_j}}}}}{{{k_j}!{{\left( {{{\bar \gamma }_j}} \right)}^{{k_1} + {{M}}}}t!\varDelta _j^{{k_j} - t + {{M}}}}}{x^t}} {{\rm{e}}^{ - {\varDelta _j}x}}} \end{split} (18) 干扰到用户的地面链路服从瑞利分布，概率密度函数和累积分布函数可以分别表示为
{f_{{\gamma _i}}}\left( x \right) = \sum\limits_{s = 1}^{\varrho \left( \mathcal{A} \right)} {\sum\limits_{n = 1}^{{\tau _l}\left( \mathcal{A} \right)} {{\chi _{s,n}}\left( \mathcal{A} \right)\frac{{\mu _{\left\langle s \right\rangle }^{ - n}}}{{\left( {n - 1} \right)!}}} } {x^{n - 1}}{{\rm{e}}^{ - \frac{x}{{{\mu _{\left\langle s \right\rangle }}}}}} (19) {F_{{\gamma _i}}}\left( x \right) = 1 - \sum\limits_{s = 1}^{\varrho \left( \mathcal{A} \right)} {\sum\limits_{n = 1}^{{\tau _l}\left( \mathcal{A} \right)} {\sum\limits_{k = 0}^{n - 1} {\frac{{{\chi _{s,n}}\left( \mathcal{A} \right)}}{{k!}}{{\left( {\frac{x}{{{\mu _{\left\langle s \right\rangle }}}}} \right)}^k}{{\rm{e}}^{ - \frac{x}{{{\mu _{\left\langle s \right\rangle }}}}}}} } } (20) 其中，
\mathcal{A} = {\rm{diag}}\left( {{\mu _1},{\mu _2}, \cdots ,{\mu _{{L}}}} \right) ,L \in \left\{ {N,M} \right\} ,\left\{ {{\mu _s}} \right\}_{s = 1}^{{L}} 代表CCI链路的平均信噪比，\varrho \left( \mathcal{A} \right) 代表\mathcal{A} 中不同对角线元素的个数，{\mu _{\left\langle 1 \right\rangle }} > {\mu _{\left\langle 2 \right\rangle }} > \cdots > {\mu _{\left\langle {\varrho \left( \mathcal{A} \right)} \right\rangle }} 代表不同对角线元素的增加序列，{\tau _l}\left( \mathcal{A} \right) 代表{\mu _{\left\langle s \right\rangle }} 的多样性，{\chi _{s,n}}\left( \mathcal{A} \right) 代表\mathcal{A} 中第\left( {s,n} \right) 个统计分量。3.2 遍历容量分析
遍历容量是经常用来评估星地融合网络性能的重要指标，是指整个通信网络所有信道的容量上限。基于NOMA的多天线星地融合网络的EC定义为不同地面接收机的信干噪比的平均瞬时互信息之和，其表示为
\begin{split} {{\rm{EC}}_{{\text{SU}}}} = & \left\{ {{\rm{E}}\left[ {{{\log }_2}\left( {1 + {\gamma _{{\text{S}}{{\text{U}}_{q - p}}}}} \right)} \right] + {\rm{E}}\left[ {{{\log }_2}\left( {1 + {\gamma _{{\text{S}}{{\text{U}}_q}}}} \right)} \right]} \right.\\ & \left. { + {\rm{E}}\left[ {{{\log }_2}\left( {1 + {\gamma _{{\text{S}}{{\text{U}}_p}}}} \right)} \right]} \right\} \\[-10pt] \end{split} (21) 将不同用户处的信干噪比式(14)、式(15)和式(16)代入EC表达式中，经过数学变换后，EC可以表示为
\begin{split} & {{{\rm{EC}}_{{\text{SU}}}} } \\ & = \frac{1}{{\ln 2}}\left\{ {\rm{E}}\left[ {\ln \left( {\frac{\sigma }{{\sigma {{\overline V }_{{e_{{\text{S}}{{\text{U}}_q}}}}} + 1}}{\lambda _{{\text{S}}{{\text{U}}_q}}} + \frac{{{\lambda _{{l_q}}}}}{{\sigma {{\overline V }_{{e_{{\text{S}}{{\text{U}}_q}}}}} + 1}} + 1} \right)} \right] \right.\\ & \quad - {\rm{E}}\left[ {\ln \left( {\frac{{{a_q}\sigma }}{{\sigma {{\overline V }_{{e_{{\text{S}}{{\text{U}}_q}}}}} + 1}}{\lambda _{{\text{S}}{{\text{U}}_q}}} + \frac{{{\lambda _{{l_q}}}}}{{\sigma {{\overline V }_{{e_{{\text{S}}{{\text{U}}_q}}}}} + 1}} + 1} \right)} \right] \\ & \quad + {\rm{E}}\left[ {\ln \left( {\frac{{\left( {{a_q} + {a_p}\xi } \right)\sigma }}{{\sigma {{\overline V }_{{e_{{\text{S}}{{\text{U}}_q}}}}} + 1}}{\lambda _{{\text{S}}{{\text{U}}_q}}} + \frac{{{\lambda _{{l_q}}}}}{{\sigma {{\overline V }_{{e_{{\text{S}}{{\text{U}}_q}}}}} + 1}} + 1} \right)} \right] \\ & \quad - {\rm{E}}\left[ {\ln \left( {\frac{{{a_p}\xi \sigma }}{{\sigma {{\overline V }_{{e_{{\text{S}}{{\text{U}}_q}}}}} + 1}}{\lambda _{{\text{S}}{{\text{U}}_q}}} + \frac{{{\lambda _{{l_q}}}}}{{\sigma {{\overline V }_{{e_{{\text{S}}{{\text{U}}_q}}}}} + 1}} + 1} \right)} \right] \\ & \quad + {\rm{E}}\left[ {\ln \left( {\frac{\sigma }{{\sigma {{\overline V }_{{e_{{\text{S}}{{\text{U}}_p}}}}} + 1}}{\lambda _{{\text{S}}{{\text{U}}_p}}} + \frac{{{\lambda _{{l_p}}}}}{{\sigma {{\overline V }_{{e_{{\text{S}}{{\text{U}}_p}}}}} + 1}} + 1} \right)} \right] \\ & \quad \left. - {\rm{E}} \left[ {\ln \left( {\frac{{{a_q}\sigma }}{{\sigma {{\overline V }_{{e_{{\text{S}}{{\text{U}}_p}}}}} + 1}}{\lambda _{{\text{S}}{{\text{U}}_p}}} + \frac{{{\lambda _{{l_p}}}}}{{\sigma {{\overline V }_{{e_{{\text{S}}{{\text{U}}_p}}}}} + 1}} + 1} \right)} \right] \right\} \end{split} (22) 为了简化分析，采用变量替换，
{A_1} = \dfrac{\sigma }{{\sigma {{\overline V }_{{e_{{\text{S}}{{\text{U}}_q}}}}} + 1}} ,{A_2} = \dfrac{{{a_q}\sigma }}{{\sigma {{\overline V }_{{e_{{\text{S}}{{\text{U}}_q}}}}} + 1}} ,{A_3} = \dfrac{{\left( {{a_q} + \xi {a_p}} \right)\sigma }}{{\sigma {{\overline V }_{{e_{{\text{S}}{{\text{U}}_q}}}}} + 1}} ,{A_4} = \dfrac{{\xi {a_p}\sigma }}{{\sigma {{\overline V }_{{e_{{\text{S}}{{\text{U}}_q}}}}} + 1}} ,{A_5} = \dfrac{\sigma }{{\sigma {{\overline V }_{{e_{{\text{S}}{{\text{U}}_p}}}}} + 1}} ,{A_6} = \dfrac{{{a_q}\sigma }}{{\sigma {{\overline V }_{{e_{{\text{S}}{{\text{U}}_p}}}}} + 1}} ,{B_1} = \dfrac{1}{{\sigma {{\overline V }_{{e_{{\text{SU}}q}}}} + 1}} ,{B_2} = \dfrac{1}{{\sigma {{\overline V }_{{e_{{\text{S}}{{\text{U}}_p}}}}} + 1}} 。此时，EC公式可以表示为\begin{split} {{\rm{EC}}_{{\text{SU}}}} = & \frac{1}{{\ln 2}}\left\{ {\rm{E}}\left[ {\ln \left( {{A_1}{\lambda _{{\text{S}}{{\text{U}}_q}}} + {B_1}{\lambda _{{l_q}}} + {\text{1}}} \right)} \right] \right.\\ & - {\rm{E}}\left[ {\ln \left( {{A_2}{\lambda _{{\text{S}}{{\text{U}}_q}}} + {B_1}{\lambda _{{l_q}}} + {\text{1}}} \right)} \right] \\ & + {\rm{E}}\left[ {\ln \left( {{A_3}{\lambda _{{\text{S}}{{\text{U}}_q}}} + {B_1}{\lambda _{{l_q}}} + {\text{1}}} \right)} \right] \\ & - {\rm{E}}\left[ {\ln \left( {{A_4}{\lambda _{{\text{S}}{{\text{U}}_q}}} + {B_1}{\lambda _{{l_q}}} + {\text{1}}} \right)} \right] \\ & + {\rm{E}}\left[ {\ln \left( {{A_5}{\lambda _{{\text{S}}{{\text{U}}_p}}} + {B_2}{\lambda _{{l_p}}} + {\text{1}}} \right)} \right] \\ & \left.- {\rm{E}}\left[ {\ln \left( {{A_6}{\lambda _{{\text{S}}{{\text{U}}_p}}} + {B_2}{\lambda _{{l_p}}} + {\text{1}}} \right)} \right] \right\} \end{split} (23) 令
{\lambda _{{{\rm{SU}}_q}}} = {x_1} ,{\lambda _{{l_2}}} = {y_1} ,{A_1}{\lambda _{{\text{S}}{{\text{U}}_q}}} + {B_1}{\lambda _{{l_2}}} = {z_1} ，采用数学变换可得{f_{{z_1}}}\left( z \right) = \int\limits_0^\infty {\frac{1}{{{A_1}{B_1}}}{f_Y}\left( {\frac{{z - u}}{{{B_1}}}} \right)} {f_X}\left( {\frac{u}{{{A_1}}}} \right){\rm{d}}u (24) 将SR分布和瑞利分布表达式(17)、式(19)代入，可得
\begin{split} {f_{{z_1}}}\left( z \right) =& {{\alpha _{{\text{S}}{{\text{U}}_q}}^{{M}}}/ {\varGamma \left( {{M}} \right)}}\\ & \cdot\sum\limits_{k = 0}^{{{M}}\left( {{m_{{{\rm{SU}}_q}}} - 1} \right)} \frac{{{{\left( {{{M}}\left( {1 - {m_{{\text{S}}{{\text{U}}_q}}}} \right)} \right)}_k}{{\left( { - {\delta _{{\text{S}}{{\text{U}}_q}}}} \right)}^k}}}{{{{\left( {k!} \right)}^2}{{\left( {{{\bar \gamma }_{{\text{S}}{{\text{U}}_q}}}} \right)}^{k + 1}}}}\\ & \cdot\sum\limits_{s = 1}^{\varrho \left( A \right)} {\sum\limits_{n = 1}^{{\tau _l}\left( A \right)} {\sum\limits_{t = 0}^{n - 1} {\frac{{{{\left( { - 1} \right)}^t}{\chi _{s,n}}\left( A \right)\mu _{\left\langle s \right\rangle }^{ - n}}}{{\left( {n - 1} \right)!}}} } } \\ & \cdot \left( {\begin{array}{*{20}{c}} {n - 1} \\ t \end{array}} \right)\left( {k + t + {{M}} - 1} \right)!\frac{1}{{A_1^{k + {{M}}}B_1^n}}\\ & \cdot{\left( {\frac{{{\varDelta _{{\text{S}}{{\text{U}}_q}}}}}{{{A_1}}} - \frac{1}{{{B_1}{\mu _{\left\langle s \right\rangle }}}}} \right)^{ - \left( {k + t + {{M}}} \right)}}{z^{n - 1 - t}}{{\rm{e}}^{ - \frac{z}{{{B_1}{\mu _{\left\langle s \right\rangle }}}}}} \end{split} (25) 同理可以得到其余部分对应的PDF。
同时，本文将EC公式改写为
\begin{split} {{\rm{EC}}_{{\text{SU}}}} =& \frac{1}{{\ln 2}}\left\{ \underbrace {\int\limits_0^\infty {\ln \left( {z + 1} \right){f_{{z_1}}}\left( z \right){\rm{d}}z} }_{{E_1}}\right. \\ & - \underbrace {\int\limits_0^\infty {\ln \left( {z + 1} \right){f_{{z_2}}}\left( z \right){\rm{d}}z} }_{{E_2}} \\ &+ \underbrace {\int\limits_0^\infty {\ln \left( {z + 1} \right){f_{{z_3}}}\left( z \right){\rm{d}}z} }_{{E_3}} \\ & - \underbrace {\int\limits_0^\infty {\ln \left( {z + 1} \right){f_{{z_4}}}\left( z \right){\rm{d}}z} }_{{E_4}} \\ &+ \underbrace {\int\limits_0^\infty {\ln \left( {z + 1} \right){f_{{z_5}}}\left( z \right){\rm{d}}z} }_{{E_5}} \\ & \left.- \underbrace {\int\limits_0^\infty {\ln \left( {z + 1} \right){f_{{z_6}}}\left( z \right){\rm{d}}z} }_{{E_6}} \right\} \end{split} (26) 采用文献[22]中的公式8.4.6.5，并利用Meijer-G函数[21]，可以得到
\ln \left( {1 + z} \right) = G_{22}^{12}\left( {z\left| {\begin{array}{*{20}{c}} {1}&1 \\ 1&0 \end{array}} \right.} \right) (27) 将式(27)和式(25)代入
{E_1} 中，利用文献[22]中的公式2.24.3.1和8.2.2.14，{E_1} 可以重新表示为\begin{split} {E_1} =& {{\alpha _{{\text{S}}{{\text{U}}_q}}^{{M}}}/ {\varGamma \left( {{M}} \right)}}\\ & \cdot\sum\limits_{k = 0}^{{{M}}\left( {{m_{{{\rm{SU}}_q}}} - 1} \right)} \frac{{{{\left( {{{M}}\left( {1 - {m_{{\text{S}}{{\text{U}}_q}}}} \right)} \right)}_k}{{\left( { - {\delta _{{\text{S}}{{\text{U}}_q}}}} \right)}^k}}}{{{{\left( {k!} \right)}^2}{{\left( {{{\bar \gamma }_{{\text{S}}{{\text{U}}_q}}}} \right)}^{k + 1}}}}\\ & \cdot\sum\limits_{s = 1}^{\varrho \left( A \right)} {\sum\limits_{n = 1}^{{\tau _l}\left( A \right)} {\frac{{{\chi _{s,n}}\left( A \right)\mu _{\left\langle s \right\rangle }^{ - t}}}{{\left( {n - 1} \right)!}}} } \sum\limits_{t = 0}^{n - 1} {\left( {\begin{array}{*{20}{c}} {n - 1} \\ t \end{array}} \right)} {\left( { - 1} \right)^t} \\ & \cdot \left( {k + t + {{M}} - 1} \right)!\frac{1}{{A_1^{k + {{M}}}B_1^t}}\\ & \cdot{\left( {\frac{{{\varDelta _{{\text{S}}{{\text{U}}_q}}}}}{{{A_1}}} - \frac{1}{{{B_1}{\mu _{\left\langle s \right\rangle }}}}} \right)^{ - \left( {k + t + {{M}}} \right)}}\\ & \cdot G_{32}^{13}\left( {{B_1}{\mu _{\left\langle s \right\rangle }}\left| {\begin{array}{*{20}{c}} {1 - n + t,1,1} \\ {1,0} \end{array}} \right.} \right) \\[-21pt] \end{split} (28) 同理可以得到其他分量的表达式。
在此基础上，经过简单的整理，最终EC的表达式可以推导为
\begin{split} {{\rm{EC}}_{{\text{SU}}}} =& \frac{1}{{\ln 2}}\frac{{\alpha _{{{\rm{SU}}_q}}^{{M}}}}{{\varGamma \left( {{M}} \right)}}\\ & \cdot\sum\limits_{k = 0}^{{{M}}\left( {{m_{{\text{S}}{{\text{U}}_q}}} - 1} \right)} \frac{{{{\left( {{{M}}\left( {1 - {m_{{\text{S}}{{\text{U}}_q}}}} \right)} \right)}_k}{{\left( { - {\delta _{{\text{S}}{{\text{U}}_q}}}} \right)}^k}}}{{{{\left( {k!} \right)}^2}{{\left( {{{\bar \gamma }_{{\text{S}}{{\text{U}}_q}}}} \right)}^{k + 1}}}}\\ & \cdot\sum\limits_{s = 1}^{\varrho \left( A \right)} {\sum\limits_{n = 1}^{{\tau _l}\left( A \right)} {\sum\limits_{t = 0}^{n - 1} {\frac{{{{\left( { - 1} \right)}^t}{\chi _{s,n}}\left( A \right)}}{{\left( {n - 1} \right)!\mu _{\left\langle s \right\rangle }^t}}} } } \\ & \cdot G_{32}^{13}\left( {{B_1}{\mu _{\left\langle s \right\rangle }}\left| {\begin{array}{*{20}{c}} {1 - n + t,1,1} \\ {1,0} \end{array}} \right.} \right) \\ & \cdot \left( {\begin{array}{*{20}{c}} {n - 1} \\ t \end{array}} \right)\left( {k + t + {{M}} - 1} \right)!\\ & \cdot\left\{ \frac{1}{{A_1^{k + {{M}}}B_1^t}}{{\left( {\frac{{{\varDelta _{{\text{S}}{{\text{U}}_q}}}}}{{{A_1}}} - \frac{1}{{{B_1}{\mu _{\left\langle s \right\rangle }}}}} \right)}^{ - \left( {k + t + {{M}}} \right)}} \right.\\ & - \frac{1}{{A_2^{k + {{M}}}B_1^t}}{{\left( {\frac{{{\varDelta _{{\text{S}}{{\text{U}}_q}}}}}{{{A_2}}} - \frac{1}{{{B_1}{\mu _{\left\langle s \right\rangle }}}}} \right)}^{ - \left( {k + t + {{M}}} \right)}} \\ & + \frac{1}{{A_3^{k + {{M}}}B_1^t}}{{\left( {\frac{{{\varDelta _{{\text{S}}{{\text{U}}_q}}}}}{{{A_3}}} - \frac{1}{{{B_1}{\mu _{\left\langle s \right\rangle }}}}} \right)}^{ - \left( {k + t + {{M}}} \right)}} \\ & \left. - \frac{1}{{A_4^{k + {{M}}}B_1^t}}\left( \frac{{{\varDelta _{{\text{S}}{{\text{U}}_q}}}}}{{{A_4}}} - \frac{1}{{{B_1}{\mu _{\left\langle s \right\rangle }}}} \right)^{ - \left( {k + t + {{M}}} \right)} \right\} \\ &+ \frac{1}{{\ln 2}}\frac{{\alpha _{{\text{S}}{{\text{U}}_p}}^{{M}}}}{{\varGamma \left( {{M}} \right)}} \\ &\cdot \sum\limits_{k = 0}^{{{M}}\left( {{m_{{\text{S}}{{\text{U}}_p}}} - 1} \right)} {\frac{{{{\left( {{{M}}\left( {1 - {m_{{\text{S}}{{\text{U}}_p}}}} \right)} \right)}_k}{{\left( { - {\delta _{{\text{S}}{{\text{U}}_p}}}} \right)}^k}}}{{{{\left( {k!} \right)}^2}{{\left( {{{\bar \gamma }_{{\text{S}}{{\text{U}}_p}}}} \right)}^{k + 1}}}}}\\ & \cdot\sum\limits_{s = 1}^{\varrho \left( A \right)} {\sum\limits_{n = 1}^{{\tau _l}\left( A \right)} {\sum\limits_{t = 0}^{n - 1} {\frac{{{{\left( { - 1} \right)}^t}{\chi _{s,n}}\left( A \right)}}{{\left( {n - 1} \right)!\mu _{\left\langle s \right\rangle }^t}}} } } \\ & \cdot G_{32}^{13}\left( {{B_2}{\mu _{\left\langle s \right\rangle }}\left| {\begin{array}{*{20}{c}} {1 - n + t,1,1} \\ {1,0} \end{array}} \right.} \right) \\ & \cdot \left( {\begin{array}{*{20}{c}} {n - 1} \\ t \end{array}} \right)\left( {k + t} \right)!\\ & \cdot\left\{ \frac{1}{{A_5^{k + {{M}}}B_2^t}}{{\left( {\frac{{{\varDelta _{{\text{S}}{{\text{U}}_p}}}}}{{{A_5}}} - \frac{1}{{{B_2}{\mu _{\left\langle s \right\rangle }}}}} \right)}^{ - \left( {k + t + {{M}}} \right)}} \right.\\ & \left.- \frac{1}{{A_6^{k + {{M}}}B_2^t}}{{\left( {\frac{{{\varDelta _{{\text{S}}{{\text{U}}_p}}}}}{{{A_6}}} - \frac{1}{{{B_2}{\mu _{\left\langle s \right\rangle }}}}} \right)}^{ - \left( {k + t + {{M}}} \right)}} \right\} \end{split} (29) 4. 数据校验
采用蒙特卡罗仿真来验证非完美条件下多天线星地融合NOMA网络的性能。仿真中采用的系统参数如表1所示。卫星信道参数如表2所示。不失一般性，假设
\delta _p^2 = \delta _q^2 = {\delta ^2} ,{\bar \gamma _{{\text{S}}{{\text{U}}_p}}} = {\bar \gamma _{{\text{S}}{{\text{U}}_q}}} = \bar \gamma ,{\bar \gamma _1} = {\bar \gamma _2} = {\bar \gamma _I} ,{k_{{\text{S}}{{\text{U}}_p}}} = {k_{{\text{S}}{{\text{U}}_q}}} = k ,{\mathcal{L}_{{\text{S}}{{\text{U}}_p}}} = {\mathcal{L}_{{\text{S}}{{\text{U}}_q}}} = \mathcal{L} 。表 1 系统参数参数 数值 卫星轨道 GEO 载波频率 18 GHz 载波带宽 50 MHz 3 dB角度 0.4° 最大波束增益 48 dB 接收天线增益 4 dB 噪声温度 300 K 雨衰 \mu = - 3.125 , \delta _\zeta ^2 = 1.591 表 2 信道参数衰落程度 {m_j} {b_j} {\varOmega _j} 重度衰落(Frequent Heavy Shadowing, FHS) 1 0.063 0.0007 中度衰落(Average Shadowing, AS) 5 0.251 0.2790 轻度衰落(Infrequent Light Shadowing, ILS) 10 0.150 1.2900 图2给出了遍历容量随功率分配因子的变化趋势。首先，可以发现仿真值与理论值相一致，证明了理论推导的正确性。其次，仿真结果随着功率分配因子
{a_p} 的增大而升高。然而，从实际角度来看，当{a_p} 趋于1时，传感器用户{U_q} 的QoS和公平性要求无法满足。同时，由于功率分配的减少，用户{U_q} 的遍历容量也会损失。基于实际公平性考虑，{a_p} 的值通常选取在\left( {0.7,0.8} \right) 之间，其余仿真均采用{a_p} = 0.75 作为仿真参数。最后，仿真结果显示遍历容量随着衰落程度的减轻而增强，这与实际相一致。图3分析了遍历容量随非完美SIC系数的变化趋势，其中
\xi = 0 表示完美SIC。非完美SIC对于遍历容量的影响十分明显，随着\xi 的增大，系统的遍历容量明显变差。这是因为NOMA传感器用户在接收端采用SIC技术来接收信号，由于接收端的性能较差，即SIC技术非完美，这将对系统的传输能力造成很大的负面影响，从而减少系统的遍历容量。图4给出了遍历容量随信道估计误差的变化。由图4(a)可以看出，当系统分配更多的功率用于信号传输时，系统的遍历容量将会更高。由图4(b)可知，随着导频信号长度的增加，系统的信道估计误差将会减小，从而提升系统的遍历容量。此外，随着系统平均信噪比的增强，导频信号长度对于遍历容量的影响会减少。通过对不同信道估计误差参数的仿真可以得出，当系统具有较高的平均信噪比时，可以获得更好的CSI减轻估计误差对于系统性能的影响。
图5反映了不同CCI情况对于遍历容量的影响，其中
{\bar \gamma _I} = - \infty 代表不存在同频干扰。首先，存在同频干扰时，系统的遍历容量会有明显的减弱。此外，随着干扰功率的增大以及干扰数量的增多，系统的遍历容量会明显减小，这与现实情况相一致。5. 结论
本文结合现实条件，包括信道估计误差、非完美串行干扰消除和同频干扰，建立了一个基于NOMA的星地融合网络。这些非完美条件将会影响基于NOMA的多天线星地融合网络的遍历容量性能。为了揭示每个非完美条件参数对于系统遍历容量的影响，本文推导得到了非完美条件下的遍历容量解析表达式。最后，通过蒙特卡罗仿真对理论推导的正确性进行了验证。仿真结果揭示了每个非完美条件参数对于星地融合NOMA网络遍历容量性能的影响，从侧面反映了具备完美系统场景对于实际网络的重要性，对工程实践具有重要的指导作用。
-
NAKAMOTO S. Bitcoin: A peer-to-peer electronic cash system[EB/OL]. https://bitcoin.org/bitcoin.pdf, 2008. 曹素珍, 王斐, 郎晓丽, 等. 基于无证书的多方合同签署协议[J]. 电子与信息学报, 2019, 41(11): 2691–2698. doi: 10.11999/JEIT190166CAO Suzhen, WANG Fei, LANG Xiaoli, et al. Multi-party contract signing protocol based on certificateless[J]. Journal of Electronics &Information Technology, 2019, 41(11): 2691–2698. doi: 10.11999/JEIT190166 NARAYANAN A, BONNEAU J, FELTEN E, et al. Bitcoin and Cryptocurrency Technologies: A Comprehensive Introduction[M]. Princeton University Press, 2016. 牛淑芬, 王金风, 王伯彬, 等. 区块链上基于B+树索引结构的密文排序搜索方案[J]. 电子与信息学报, 2019, 41(10): 2409–2415. doi: 10.11999/JEIT190038NIU Shufen, WANG Jinfeng, WANG Bobin, et al. Ciphertext sorting search scheme based on b+ tree index structure on blockchain[J]. Journal of Electronics &Information Technology, 2019, 41(10): 2409–2415. 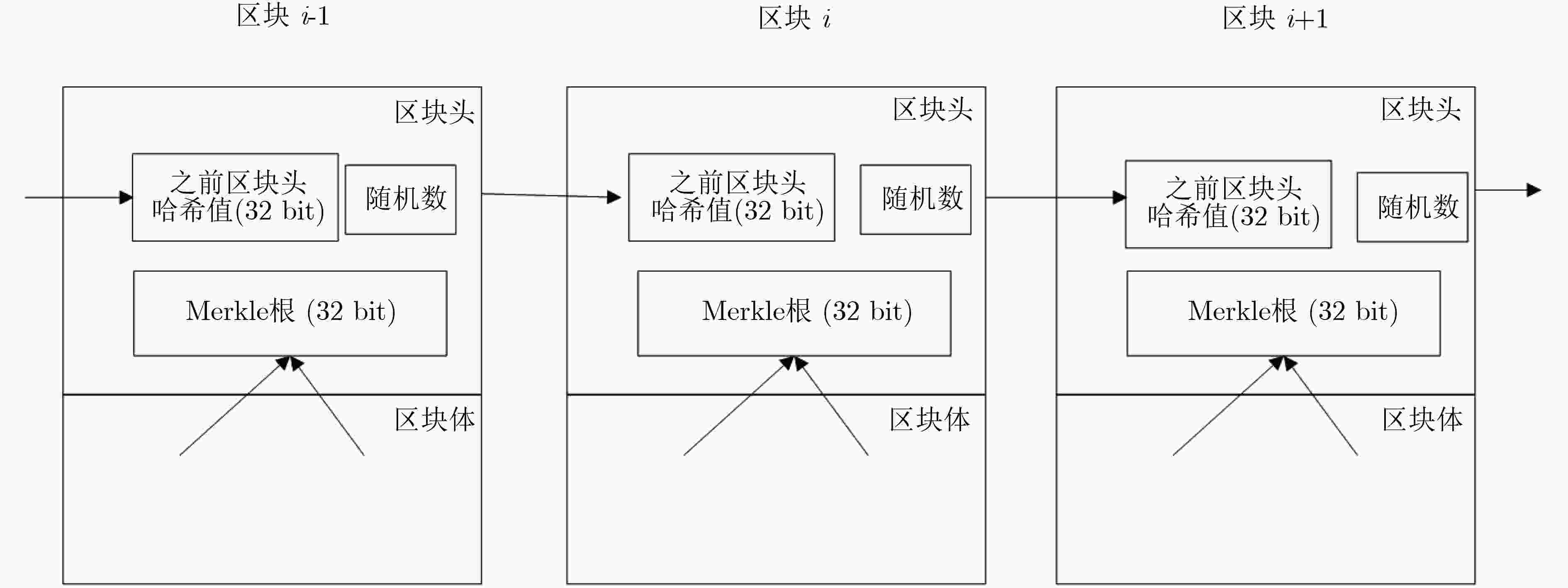doi: 10.11999/JEIT190038 邹均, 张海宁, 唐屹, 等. 区块链技术指南[M]. 北京: 机械工业出版社, 2016: 97–99.ZOU Jun, ZHANG Haining, TANG Yi, et al. Guidelines for Blockchain Technology[M]. Beijing: China Machine Press, 2016: 97–99. CHAUM D, FIAT A, and NAOR M. Untraceable Electronic Cash[M]. GOLDWASSER S. Advances in Cryptology — CRYPTO’ 88. New York: Springer, 1990: 319–327. doi: 10.1007/0-387-34799-2_25. 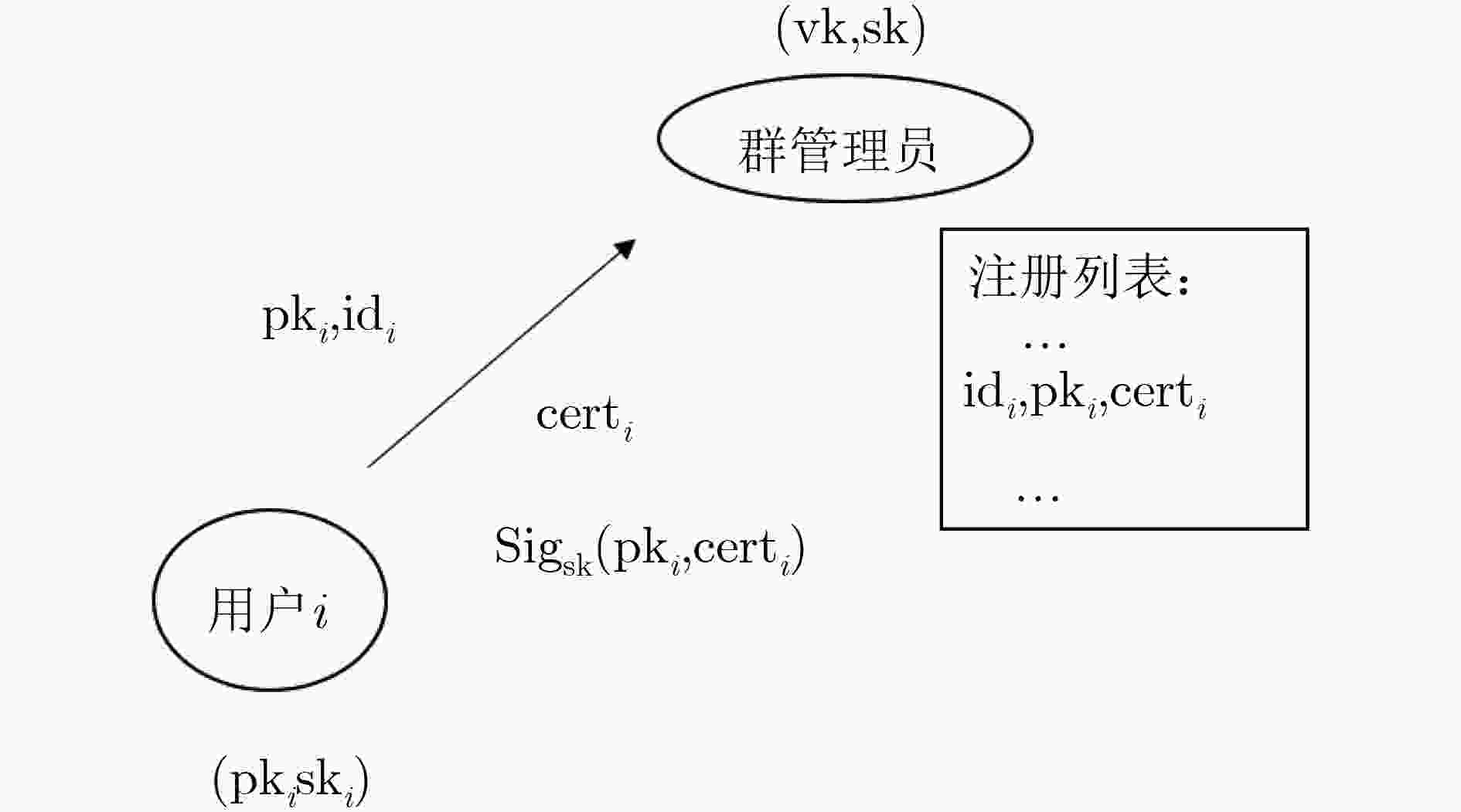CHAUM D and VAN HEYST E. Group Signatures[M]. DAVIES D W. Advances in Cryptology — EUROCRYPT ’91. Berlin: Springer, 1991: 257–265. doi: 10.1007/3-540-46416-6_22. GROTH J and SAHAI A. Efficient non-interactive proof systems for bilinear groups[C]. The 27th Annual International Conference on the Theory and Applications of Cryptographic Techniques, Istanbul, Turkey, 2008: 415–432. doi: 10.1007/978-3-540-78967-3_24. CHAUM D L. Untraceable electronic mail, return addresses, and digital pseudonyms[J]. Communications of the ACM, 1981, 24(2): 84–90. doi: 10.1145/358549.358563 BONNEAU J, NARAYANAN A, MILLER A, et al. Mixcoin: Anonymity for Bitcoin with Accountable Mixes[M]. CHRISTIN N and SAFAVI-NAINI R. Financial Cryptography and Data Security. Berlin: Springer, 2014: 486–504. doi: 10.1007/978-3-662-45472-5_31. VALENTA L and ROWAN B. BLIndcoin: Blinded, accountable mixes for bitcoin[C]. 2015 International Conference on Financial Cryptography and Data Security, San Juan, USA, 2015: 112–126. doi: 10.1007/978-3-662-48051-9_9. MAXWELL G. Coinjoin: Bitcoin privacy for the real world[EB/OL]. Post on Bitcoin Forum. https://bitcointalk.org/index.php?topic=279249.0, 2013. RUFFING T, MORENO-SANCHEZ P, and KATE A. CoinShuffle: Practical decentralized coin mixing for bitcoin[C]. The 19th European Symposium on Research in Computer Security, Wroclaw, Poland, 2014: 345–364. doi: 10.1007/978-3-319-11212-1_20. RUFFING T, MORENO-SANCHEZ P, and KATE A. P2P mixing and unlinkable bitcoin transactions[C]. The 24th Annual Network and Distributed System Security Symposium, San Diego, USA, 2017: 824. RUFFING T and MORENO-SANCHEZ P. Valueshuffle: Mixing confidential transactions for comprehensive transaction privacy in bitcoin[C]. 2017 International Conference on Financial Cryptography and Data Security, Sliema, Malta, 2017: 133–154. CHANDRAN N, GROTH J, and SAHAI A. Ring signatures of sub-linear size without random oracles[C]. The 34th International Colloquium on Automata, Languages, and Programming, Wrocław, Poland, 2007: 423–434. BERGAN T, ANDERSON O, DEVIETTI J, et al. CryptoNote v 2.0[J]. https://cryptonote.org/whitepaper.pdf, 2013. LIU J K, WEI V K, and WONG D S. Linkable spontaneous anonymous group signature for ad hoc groups[C]. The 9th Australasian Conference on Information Security and Privacy, Sydney, Australia, 2004: 325–335. doi: 10.1007/978-3-540-27800-9_28. MIERS I, GARMAN C, GREEN M, et al. Zerocoin: Anonymous distributed e-cash from bitcoin[C]. 2013 IEEE Symposium on Security and Privacy, Berkeley, USA, 2013: 397–411. BEN SASSON E, CHIESA A, GARMAN C, et al. Zerocash: Decentralized anonymous payments from bitcoin[C]. 2014 IEEE Symposium on Security and Privacy, San Jose, USA, 2014: 459–474. BEN-SASSON E, CHIESA A, TROMER E, et al. Succinct non-interactive zero knowledge for a von Neumann architecture[C]. The 23rd USENIX Conference on Security Symposium, Berkeley, USA, 2014: 781–796. PEDERSEN T P. Non-interactive and information-theoretic Secure Verifiable Secret Sharing[M]. FEIGENBAUM J. Annual International Cryptology— CRYPTO ’91. Berlin: Springer, 1991: 129–140. doi: 10.1007/3-540-46766-1_9. FUJISAKI E and SUZUKI K. Traceable ring signature[C]. The 10th International Conference on Practice and Theory in Public-Key Cryptography, Beijing, China, 2007: 181–200. doi: 10.1007/978-3-540-71677-8_13. GROTH J. Fully anonymous group signatures without random oracles[C]. The 13th International Conference on the Theory and Application of Cryptology and Information Security, Kuching, Malaysia, 2007: 164–180. doi: 10.1007/978-3-540-76900-2_10. ZHOU Sujing and LIN Dongdai. Shorter Verifier-local Revocation Group Signatures from Bilinear Maps[M]. POINTCHEVAL D, MU Yi, and CHEN Kefei. Cryptology and Network Security. Berlin: Springer, 2006: 126–143. doi: 10.1007/11935070_8. BONEH D and BOYEN X. Short Signatures without Random Oracles[M]. CACHIN C and CAMENISCH J L. Advances in Cryptology - EUROCRYPT 2004. Berlin: Springer, 2004: 56–73. doi: 10.1007/978-3-540-24676-3_4. 期刊类型引用(3)
1. 安秀娟，王兆荣，张东坡. 非正交多址接入异构网络用户公平性问题研究. 现代电子技术. 2024(13): 61-65 . 
百度学术2. 谈苗苗，孔槐聪，黄庶沛，程铭，林敏. 基于上/下行NOMA的卫星通信系统遍历容量分析. 南京航空航天大学学报. 2023(05): 780-788 . 百度学术3. 溪利亚，王舜燕. 无线网络中多址接入协议仿真测试. 计算机仿真. 2023(10): 249-253 . 百度学术其他类型引用(1)
-
下载:
百度学术
计量
- 文章访问数: 4911
- HTML全文浏览量: 2344
- PDF下载量: 461
- 被引次数: 4
下载:
